GeoGebra辅助正方体截面问题教学

2022-01-10广东省广州市天河中学510623

中学数学研究(广东) 2021年22期

广东省广州市天河中学(510623) 郭靖

1 一道关于正方体截面问题的高考题引入

GeoGebra=Geometry(几何)+Algebra(代数),是一款开源免费、功能强大、适合教与学的动态数学软件,具有以下特点:①功能多样,适用于函数、几何、立体几何、统计、图表等运算与展示; ②操作简便,初学者可以点击工具栏作图,高阶用户可通过命令、脚本制作可交互的课件; ③资源丰富,通过官方开源社区免费进行作品、课件的交流与分享.下面就立体几何中常见的正方体截面问题谈谈如何利用GeoGebra 进行探究.

2018年全国理科Ⅰ卷第12 题:已知正方体的棱长为1,每条棱所在直线与平面α所成的角相等,则α截此正方体所得截面面积的最大值为( ).

和这道题类似的变式题:在正方体ABCD-A1B1C1D1中,用空间中与该正方体所有棱所成角都相等的平面α去截正方体,在截面边数最多时的所有多边形中,多边形截面的面积为S,周长为l,则( ).

A.S为定值,l不为定值

B.S不为定值,l为定值

C.S与l均为定值

D.S与l均不为定值

通过对这两道题目的分析,我们发现平面α与正方体每条棱所成的角均相等,其实正方体共有12 条棱,按方向分为三组,每组中的四条棱是平行的.因此只要和共顶点的三条棱所成的角相等就行了.很容易发现与平面A1BD平行的面且截面是六边形时满足条件(如图1 所示).

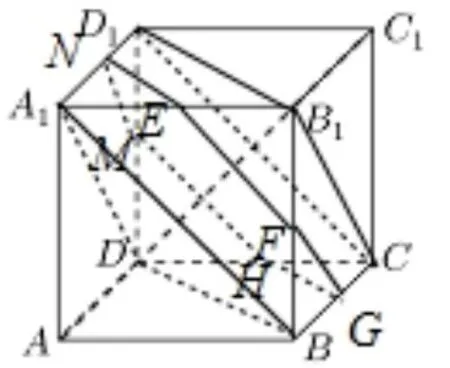
图1

其实此截面是动态变化的,在变化过程中始终保持与正方体对角线垂直.那么这种截面是如何变化的呢? 变化过程中截面面积与周长又有什么变化呢? 下面我们采用GeoGebra Classic 5 进行探究.

1.1 建立正方体

在视图下拉列表中打开3D 绘图区,在快捷按钮中选择正六面体,构造出正方体(如图2).

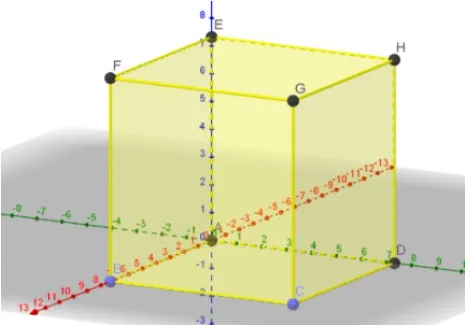
图2

1.2 建立截面

选择作线段工具,构造正方体对角线.新建滑动条,区间变化最小值为0,最大值为1,增量为0.01.输入指令“描点(<正方体对角线>,<滑动变量>)”.在指令栏选择垂直平面,构造过正方体对角线上的点且与对角线垂直的平面α(如图3).

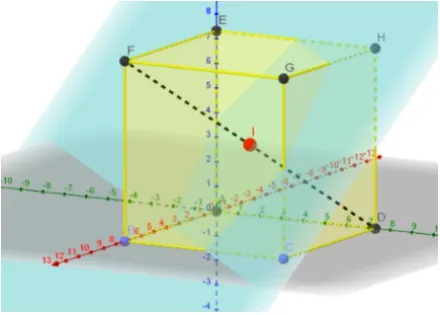
图3

1.3 观察截面变化

选择相交曲线指令,然后分别点击截面与正方体,得到截面与正方体相交的截面.隐藏坐标轴以及原本的截面.选中截面,按右键创建平面视图,得到截面的平面图(如图4).

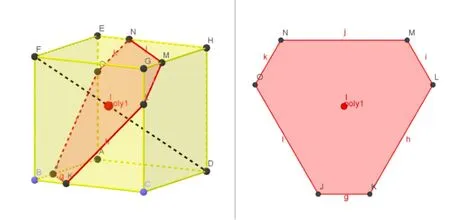
图4

1.4 度量截面面积与周长

把代数区的poly1 拉到绘图区,这个就是截面面积,可以看出随着截面形状变化,截面的面积也在变化,并且可以发现当截面经过正方体对角线中点时,截面面积最大.度量每条边长,输入指令相加,得到截面周长,发现这是个不随截面形状变化的量.

1.5 教学初探

这道高考题以及衍生题,都涉及与正方体对角线垂直的平面截面问题.在立体几何中这是个相当抽象的问题,考察学生的空间想象能力、逻辑思维能力.围绕数学核心素养中的数学抽象和直观想象.学生在没有直观感知的情形下进行想象,是很具挑战性的.所以一直以来是教学的难点,也就是2018年高考理科压轴选择题.我在课堂上使用GeoGebra 演示,让学生对截面形状有直观感知,然后再让学生探究面积的最大值.通过演示以及直观想象,很多学生都能找出截面面积最大值时的位置.然后我再让学生通过证明和计算得到答案.这正是体现了逻辑推理和数学运算,因此我认为这道题是全方面考察核心素养的好题,而使用GeoGebra 辅助教学,能让学生更清晰地发现问题,解决问题.只有建立了对正方体直观的感知,才有可能突破难点,解决问题.因此我又变式了题目,变式题增加了周长的考察,但是在上一题的演示下,很多学生已经知道了截面形状变化规律,比较容易突破.

2 正方体截面问题

除高考题外,人教版(2019)高中数学必修第二册也有关于正方体截面的探究问题“用一个平面截一个正方体,截面分别是什么形状? ”我们来看看利用GeoGebra 如何实现.

2.1 建立正方体与球

描点A(-1,-1,-1)与点B(1,-1,-1),选择正六面体工具,再分别点击A、B来建立正方体(如图5).继续描点O(0,0,0),,选择球面(球心与一点),再分别选择O与A来建立球(如图6).

图5

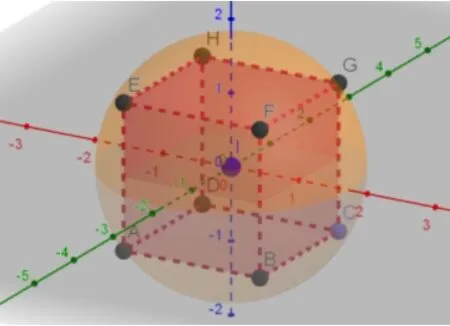
图6

建立球面上一点N,利用点工具在球面上建立一个点或输入指令“N=point(b)”.建立滑条参数t= 0.5,再建立NO直线上一点P,输入“P= (1- t)O+tN”.在GeoGebra 中点的运算和向量的运算法则是一致的,这就使得N、O、P三点共线.接下来建立平面:先设法向量n =vector(O,N),再利用垂直平面工具,对应指令为c=PerpendicularPlane(P,n).最后为了得到清晰的截面图,选择相交曲线工具,分别点击平面与正方体,隐藏不需要的坐标轴以及球.

2.2 观察截面的形状变化

通过移动N点以及滑条改变t值,可以观察到正方体截面形状的变化情况(如图7).

图7

2.3 教学初探

在探究中,让学生充分动手实验,可以通过教具或者具体物品,如切萝卜,让学生直观感知正方体截面的形状有哪些.这是考察学生动手能力以及空间思维能力.那么GeoGebra 在这里体现了演示总结的作用.

3 GeoGebra 辅助正方体截面探究的功能简介

在上述两个案例中,利用GeoGebra 中的3D 绘图功能来作图.可以直接作出多面体和旋转体,实现两个几何体的交线绘制,过一点作与已知直线或已知平面垂直的平面,以一点以及半径作球面,度量空间长度以及平面图形的面积.

4 GeoGebra 对立体几何教学的帮助

4.1 提高课堂效率

GeoGebra 可以提供快捷画图工具按钮,在3D 绘图界面就可以直接作出棱锥、棱柱、圆锥、圆柱等.还可以直接作出与已知直线或已知平面平行或垂直的平面,以及多面体展开图.这些功能都可以通过快捷键实现.教师操作方便有利于提高课堂效率.

4.2 使抽象问题直观化

利用GeoGebra 可以做出各种各样的优美图形.例如,制作动态的旋转体,立体几何图像.使用GeoGebra,可作出具有某些约束条件的几何图像,能让学生理解比较困难的几何关系,并且可以让学生在变化的图形中找到一些数学原理和几何性质,使复杂的数学难题化解成直观形象的容易题,从而培养学生的学习兴趣与维持他们学习数学的信心与勇气.

GeoGebra 的“动画”与“移动”功能使得所作的点、线、面、体都能在各自的线路上,按照各自的运动速度和运动方向实现动画或移动,能够产生非常好的动态效果.GeoGebra还可以测量角度、线段的长度、封闭图形的面积、几何体的体积等,以及构造随点、线、面、体的运动而变化的量,这样更贴近实际.从而能够更好地体现数形结合,让学生有一个直观的印象,进而产生非常好的数学教学效果[1].

4.3 提高空间思维能力

相较于当前的各类教学软件,GeoGebra 在立体几何的功能上展示出自己独特的优势[2].教师提供演示并不是代替学生思考,而是搭建平台,让学生自己直观感知,从而提高学生空间思维能力.

4.4 培养学生的探索能力

著名教育家布鲁纳说过:“探索是数学的生命线”.用GeoGebra 帮助学生观察、思考、探索,能够让学生的想象力得到充分发挥,通过GeoGebra 作动态演示,可以增强学生感性认识,把抽象的事物具体化,使学生的探索能力得到培养.尤其在立体几何的教学中,使用GeoGebra 教学手段可以方便学生学会做辅助线,能够简化空间想象能力的复杂过程,也在一定程度上训练了高中学生的动态思维,也间接地培养学生的探索能力.