基于SLAM算法的双柔性杆机器人迟滞补偿方法
2022-01-10宋婷婷
宋婷婷
(福州理工学院,福建 福州350506)
0 引言
在智能化逐渐加深的今天,机器人代替人工已经成为诸多行业的普遍现状[1].与人工生产相比,机器人生产具有减少管理任务,提高产品质量稳定性,问题溯源更加便捷的特点,但与此同时,使用机器人对产品进行加工生产的基础是对机器人的高精度控制,并且确保机器人能够准确执行输入的命令[2].因此,近些年来,关于机器人的研究逐渐成为相关学者研究的热点.研究的内容也逐渐从对功能的探索转向对运行效果的精细化研究[3].其中,一项极为重要的内容就是机器人对操作命令的迟滞问题,特别是对双操作杆的机器人而言,迟滞问题是影响其最终操作效果的关键因素[4].由于机器人在接收到操作端输入的信息后,需要对其进行解码辨识[5],当转化为实际的输出动作,出现迟滞后,会导致两个操作杆出现操作时延异常的情况,使二者之间的配合产生时间差,导致操作结果与输入结果不一致,影响最终产品的质量[6].迟滞问题已有学者作出相关研究,其中文献[7]提出对迟滞特征的非线性分析,并提出对应的补偿方法,该方法实现了降低迟滞的目的,但迟滞仍然存在;文献[8]提出基于Duhem前馈的迟滞逆补偿方法,实现了对迟滞问题的有效解决,但其需要对设备运行前期的迟滞信息进行采集,因此,存在固定时段的无效操作,对资源造成浪费,成本较高.因此,继续加强对迟滞问题的研究是十分必要的.
基于此,实验提出基于SLAM算法的双柔性杆机器人迟滞补偿方法.在分析引起迟滞原因的基础上,通过SLAM算法计算迟滞大小,以此进行有针对性的定量补偿,并通过试验验证了所提方法的有效性,为机器人的控制和高质量利用提供有价值的参考.
1 基于SLAM算法的机器人迟滞分析
为了实现对双柔性杆机器人的迟滞进行准确补偿,首先要明确机器人迟滞的变化情况[9],以此为基础,有针对性地对其进行补偿.因此,实验采用SLAM算法对机器人的迟滞非线性属性进行分析.
1.1 构建双柔性杆机器人运动轨迹模型
在双柔性杆机器人的运行空间内,其运动轨迹与动作都是通过执行控制端输入指令实现的[10].机器人在已知地图的环境中运行时,机器人可以通过观测位置已知的特征标志对里程计的误差进行补偿,每一次观测使机器人的位置误差趋向于观测误差与特征标志的位置误差之和.因此在命令输出过程中,对于机器人运行范围内的空间环境进行分析,是有效降低和避免机器人运动出现异常的基础[11].首先,采用SLAM算法对机器人的运动轨迹进行建模[12].
在运动空间,机器人在极线运动状态下的极线运动轨迹可以表示为
(1)
(2)
以此为基础,采用SLAM算法对机器人运行轨迹进行建模.将机器人运动过程中经过的位置作为SLAM算法的算子,则在t+1时刻,机器人所在运行轨迹的极线线性方程中,对应的向量分别为(ai,bi,ci),那么在t至t+1时间内,SLAM算子组成的位置方程可以表示为
l=aixi+biyi+ci
(3)
由此可得,在整个运动过程中,SLAM算子的集合即为机器人的运动轨迹,那么其运动轨迹模型可以表示为
(4)
1.2 迟滞分析
通过SLAM算子计算出了机器人运行轨迹的模型,在模型中,对机器人出现的迟滞进行分析,并将分析结果作为迟滞补偿的依据[13].
根据上述模型可以得出,在t至t+1时间内,机器人运行的距离可表示为
(5)
在该距离内,将SLAM算子的位置信息进行划分[14].首先定义一个总迟滞函数,通过将SLAM算子进行下降处理[15],以引起迟滞的运动轨迹边界类型为基础,计算机器人在d距离内运动的迟滞.
根据两个相邻SLAM算子的参数关系,可以将引起迟滞的边界可分为遮挡、铰链、共轨迹三部分[16],假设三者对应的惩罚系数分别为Hz、Hj、Hg,以此为基础,得到迟滞函数为

(6)
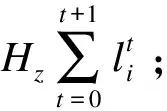
由此可以得出在不同边界条件下,机器人在运行过程中产生的迟滞,根据该结果,对其进行有针对性的迟滞补偿.
2 机器人迟滞补偿
在得出双柔性杆机器人运动状态下的迟滞后,对其进行迟滞补偿.实验采用AP(Adaptive Projection,自适应投影)的方式,在基于SLAM算法构建的机器人运动轨迹模型中对迟滞补偿量进行计算,并将计算结果以增益的方式实现对机器人的迟滞补偿.
首先,采用AP算法对SLAM算子在迟滞中的权重进行计算,其可表示为
(7)
其中,ω(t)表示在t时刻的SLAM算子的权重,λ表示自适应数,κ表示增益系数,其可根据机器人的实际运行情况进行调整,调整范围为[0,1),e(*)表示t时刻,机器人运动出现的迟滞.
在机器人完成系统输入指令的过程中,由于其运动轨迹是非线性的,因此增益系数也是时刻变化的.当机器人产生的迟滞明显时,需要适当减小增益系数,以此避免出现迟滞补偿过量.
在对增益进行调节时,以SLAM算子的实际位置信息与模型中位置信息之间的差异作为判断依据的,并在二者之间建立了线性相关关系.其可表示为
κ=ke(t)
(8)
其中,k表示相关系数,其与机器人的控制系统相关.同样地,当增益系数为最大值,迟滞补偿的作用仍无法实现对机器人运动轨迹控制的目标时,以最大值作为增益输出值;当增益系数为最小值,迟滞补偿仍超出对机器人运动轨迹控制所需强度时,以最小值作为增益输出值.
通过这样的方式,在模型中实现对增益取值结果合理性验证,由于机器人的运行是动态的,因此在增益作用下,当SLAM算子的位置信息与模型一致时,则认为该增益可以实现双柔性杆机器人迟滞补偿,此时机器人完成指令任务的时延也为最小值;若在增益作用下,SLAM算子的位置信息与模型存在差异,则表明迟滞出现了相对变化,此时需要对增益值进行调整,通过自适应投影的方式计算出新的增益值,重新进行验证,直至满足要求.
3 试验测试
为了测试提出的机器人迟滞补偿方法的实际应用效果,文章进行了试验测试,同时,为了使测试结果具有更高的可靠性,分别采用文献[7]和文献[8]提出的补偿方法同时进行试验,通过对比不同补偿方法下机器人的运行情况,对提出方法的有效性进行客观评价.
3.1 测试环境
试验选用某汽车配件制造厂的双柔性杆机器人作为试验对象,其操作精度为0.1 mm,机械臂的最高移动速度为1.2 m/s,运行范围为3 m×2 m×5 m.工作过程中,双臂同时进行操作,其编号分别为1、2.机械臂由同一台主机控制,操作系统为Windows 8,运行内存为4G.在试验过程中,分别设计了10个不同的操作动作,对应编号为1—10,每个编号指令均测试10次,取平均值.通过不同的迟滞补偿方法,对机器人的动作执行进行控制,并观察不同方法下机器人的运动情况.
3.2 测试结果
在上述试验环境下,分别采用3种方法对其进行迟滞补偿,并对比不同补偿方式下机器人的运行情况,图1分别对比了机器人双臂运动时延的差异情况.
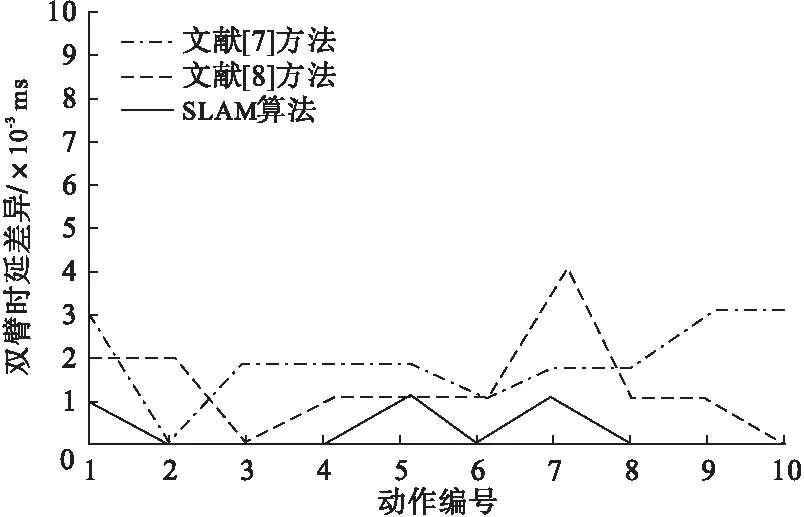
图1 不同补偿方法下机器人双臂的时延差异
从图1中可以看出,在3种补偿方法中,文献[7]方法下机器人双臂的最小时延差异为0,最大时延差异为0.02 ms,文献[8]方法下机器人双臂的最小时延差异同样为0,最大时延差异为0.04 ms,而采用本方法的机器人双臂时延差异为0的概率为70%,其余时延也仅为0.01 ms,表明SLAM算法的迟滞补偿方法可以有效提高机器人双臂执行指令的同步程度,为加工质量提供保障.这主要是因为该方法降低了机器人运行过程中的迟滞,减少了由此带来的时间开销,缩短了完成指令动作的时延.
在此基础上,对机器人双臂的运动精度进行比较,表1为不同补偿方法下机器人双臂的运动误差情况.
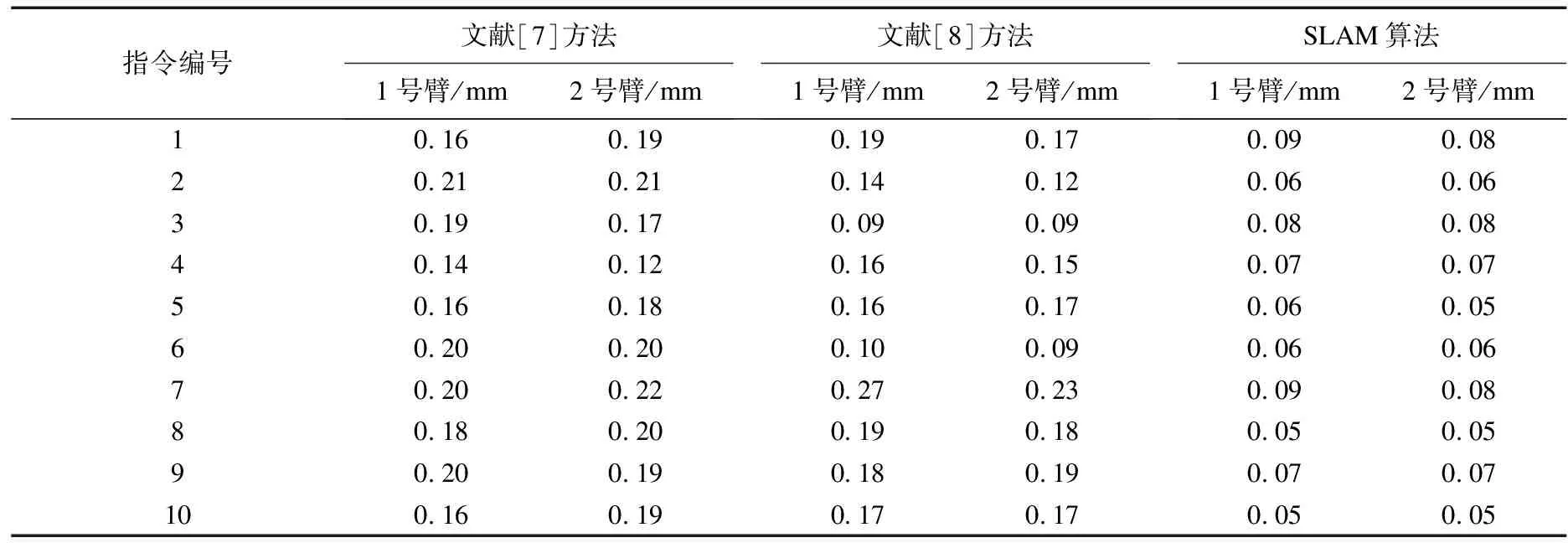
表1 不同补偿方法下机器人双臂的运动误差
从表1中可以看出,在3种迟滞补偿方法中,文献[7]方法下机器人双臂的运动误差基本稳定在0.1~0.2 mm范围内,文献[8]方法的时延变化范围较大,最高值可达到0.27 ms,但最小误差低至0.09 mm,稳定性较低,而SLAM算法的误差始终稳定在0.1 mm以内,且最小值仅为0.05 mm,表明该方法可以有效实现对机器人迟滞的补偿,降低其对接收到指令的执行精度.主要是因为SLAM算法实现了对迟滞的准确计算,提高了迟滞补偿的目标精度,使补偿结果更加精准,以此提高了机器人运行的精度.
在上述基础上,文章对3种补偿方法下,机器人执行指令的结果与指令的一致性进行对比,其结果如图2所示.从图2中可以看出,在3种补偿方法中,文献[7]方法的指令完成率基本在96%~98%之间,波动范围相对较小,但执行结果存在一定的提升空间;文献[8]方法的完成率波动幅度较大,最高可达99.26%,但最低仅为95.17%,对产品质量的影响较为明显,这也和机器人双臂的时延差异较大有一定关系;而SLAM算法的完成率始终在99%以上,具有较高的执行率,可实现对指令的高精度执行,因此,产品质量也可以实现有效保障.这主要是因为SLAM算法实现了对机器人迟滞的有效补偿,通过在模型中对补偿结果进行验证,避免了由于机器人的动态变化引起的补偿效果不理想的问题,以此提高了机器人运行的精度,使其能够更加准确地执行接收到的指令信息.

图2 不同补偿方法下机器人的指令完成情况
4 结束语
随着现代技术的不断发展,工业领域的智能化程度也不断加深,机器人取代人工已经成为主流趋势.与此同时,提高机器人的应用性能是确保生产各个环节稳定运行的基础,也是产品质量的重要的保障.文章提出基于SLAM算法的双柔性杆机器人迟滞补偿方法,通过对引起机器人迟滞的问题进行分析,有针对性地进行补充,实现了降低机器人运行时延,提高反应速率的目的,并在一定程度上降低了由于输入端与反馈端时间差引起的产品质量问题,对于机器人的控制以及企业的实际生产都具有十分重要的现实意义.通过该研究,可以为机器人领域的研究提供有价值的参考.
