基于神经网络和准同步采样算法的电力谐波分析

彭大铭 ，肖伸平 ，周欢喜

（1.湖南工业大学 电气与信息工程学院，湖南 株洲 412007；2.电传动控制与智能装备湖南省重点实验室，湖南 株洲 412007；3. 湖南宏动光电有限公司，湖南 长沙 410000）

0 引言

当正弦基波电压施加到非线性设备上时，设备所吸收电流的波形若与施加电压的不同，电流则发生畸变，产生谐波。在现代电力系统中，随着大量非线性负荷的投入运行，越来越多的谐波涌入电网，使得电网中由谐波污染引起的电能质量问题越来越严重[1-2]。通常，为了治理谐波污染，精确估计谐波分量参数（如幅值和相角）是首要步骤。通常用于估计谐波分量的方法有快速傅里叶(fast Fourier transform，FFT)变换、人工神经网络及小波分析等。其中，FFT是应用最广泛的方法；但是实际应用中很难实现同步采样，而在非同步采样下的FFT会出现频谱泄漏和栅栏效应，使得谐波检测结果的精度很低，尤其是相位误差较大，不能满足谐波检测的要求。解决这个问题有两种常用的方法：加窗插值算法和准同步采样算法[3-5]。常用的窗口函数有汉宁窗、布莱克曼窗口和Nutall窗等[6-9]。准同步采样算法也可被看作是一种窗函数算法，在非同步采样条件下，它能达到接近同步采样条件下的测量精度，但代价是需要更多的测量数据和时间。神经网络算法在谐波分析中的应用目前仍处于发展阶段[10-13]。前期，学者们讨论了用人工神经网络代替模拟并联谐波测量装置中的带通滤波器，然后构造了一种特殊的多层前馈神经网络来实时测量谐波，并分析了多层前馈神经网络的训练方法和训练样本的组成，仿真结果验证了所提出的谐波测量方法的有效性。然而，多层前馈自适应人工神经网络的训练过程是不确定的，应用前需要大量的训练；神经网络的神经元更多，计算量更大。后来，有学者提出将神经网络与快速傅里叶变换模型相结合，成了神经网络算法进行谐波分析的主流用法。文献[11]构造了一种隐神经元为正弦函数的BP（back propagation）神经网络，其推导了迭代步长的选用范围。在BP神经网络的基础上，文献[12]中应用了基于隐藏神经元的数量选择迭代步长。文献[11-12]的方法都是基于理想基波频率获得的前提。然而在实际情况下，如电力环境中，电信号频率处于波动中，高精度的基波频率是无法被直接获取的。学者们还探索了使用其他的算法为神经网络确定初值，比如结合现代谱分析中的算法。文献[13]提出了应用快速TLS-ESPRIT(总体最小二乘法—旋转矢量不变技术)来获取信号的频率成分，并将其作为神经网络的初始值。这种方法更加完备，但在分析整次谐波上，精度有不少降低。

针对理想的基波频率无法被直接获取的问题，同时为了保持神经网络在整次谐波分析中的高精度，本文提出一种将准同步采样算法和神经网络算法相结合的方法，即应用准同步采样算法为神经网络提供高精度的基波频率估计值，利用神经网络算法进行最速下降法的步长寻优，从而提高电力谐波分析的精度和速度。

1 准同步采样算法

准同步采样算法在频率分析中已得到了广泛的应用，本文在准同步采样算法的基础上，给出了通常情况下的准同步窗系数的直接表达式。相较于传统的递归方式，通过表达式直接求取准同步窗系数更为快速。

1.1 采用同步采样算法估计基波频率

假设测量的信号为

式中：f——信号基波频率；A0——直流分量；Am——谐波的幅度；φm——谐波的相位；m——谐波次数；M——最大谐波次数。

信号基波频率，f=fNs+fΔ，其中fNs为将N个采样作为一体所对应的频率（N为单次准同步递归运算的使用的数据量，N∈Z+，fNs=fs/N，fs是采样频率）；fΔ是频偏。

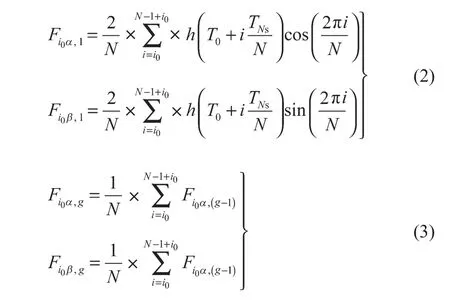
式中：g=2, 3, …,n；i0——递归运算的起点，i0=0, …,n(N-1)，i0=0意味着算法起点和采样起点重合；T0——采样的起点；n——递归次数，n∈Z+；TNs——N次采样所需的时间，TNs=1/fNs。

图1示出n=4时准同步采样算法的递归过程，其中，hi表示第i+1个采样数据；F0,n表示F0α,n或F0β,n，两者的计算过程是类似的。

图1 n=4时准同步采样算法递归过程Fig. 1 Iteration process based on the quasi synchronous sampling algorithm as n=4

展开式(2)和式(3)，得到

式中：ηi——总加权系数，即准同步窗系数，由于这里已经确定复化梯形求积方式，所以ηi仅仅由n和N来确定。

在一些情况下，由于早已确定了n和N，可以提前计算ηi并储备在计算机里。可以看出，如果能够用简单的表达式求取，则可通过式(4)直接求得F0α,n或F0β,n，这相比通过式(2)和式(3)的递推方法求取无疑将节省不少计算时间。后文将推导准同步窗系数的表达式，在此先介绍用准同步算法计算基波频率的方法。

假设同一批采样数据的两组递归运算的起点不同，它们与采样起点之间的时间间隔分别为0和t0，两组递归运算的结果分别记作Fα,n(0)和Fβ,n(0)，Fα,n(t0)和Fβ,n(t0)，那么当满足一些通常符合的基本条件[5]且n较大时（如n=3或4），有

由于t0已知，所以可以由式(5)估算出频偏fΔ，并通过式(6)计算出基波频率：

1.2 准同步窗系数直接表达式

对于不同的n和N值，准同步窗系数是不一样的。首先论证准同步窗系数的序列是对称的，即ηj=ηn(N-1)-j，j=0, 1, …,n(N-1)。显然，当n=1 时，可以得到

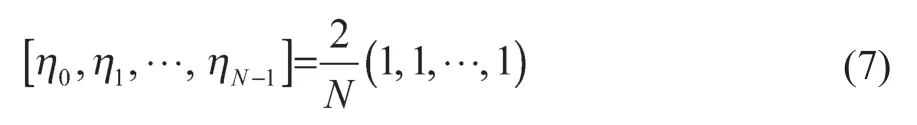
当n=1时，窗系数的序列是对称的。假设当n=k时，窗口系数序列也是对称的，并令

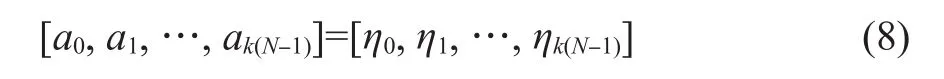
这里使用符号a表示n=1时的窗系数，则

当n=k+1时，令

通过式(2)～式(4)和式(8)，可以得到

结合式(9)和式(11)，可以推断出

至此，也就论证了窗系数的对称性；同时借由式(11)，可以由n=1的窗系数表达式依次推出n取各个整数的窗系数表达式。但由于通常取n等于3或4，而n的取值越高意味着算法精度越高，所以接下来只给出n=4时的窗函数系数表达式：

其中：

通过窗系数表达式,在n=4时，计算窗系数序列需要进行[7(N-1)+1]次加法和[5(N-1)+2]次乘法计算；但按照传统的递归方法[14]，则需要进行(4.5N2-1.5N)次加法计算。实际采样时，采样频率一般为信号基波频率的几十倍，而N的取值为采样频率对基波频率的倍数的临近值，故一般情况通过表达式直接求取的方法较大程度地减少了准同步窗系数的计算量。

2 神经网络模型和步长寻优

神经网络谐波分析算法通常是通过构造一种等同FFT模型的BP神经网络来迭代计算谐波成分；而在神经网络的迭代计算中，步长的选择是一个影响迭代速度和迭代能否实现的要点。

2.1 神经网络模型

式(1)所示测量信号可以被改写为

式中：A0为直流分量；Am为谐波幅值，Bm=Amcosφm，Cm=Amcosφm。

在已知Bm和Cm的情况下，可以根据式(16)和式(17)分别计算谐波的幅度和相位：

2.1.1 建模

基于式(15)，可以构造一个以三角函数作为隐藏层的激活函数，其输入为时间、权重对应于幅值的神经网络模型（也可视作一种FFT模型），如图2所示。

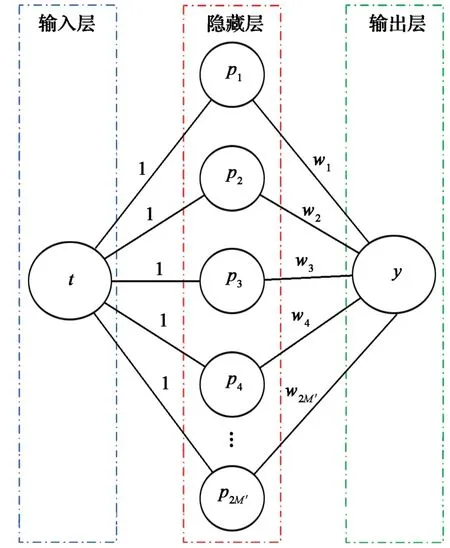
图2 神经网络模型Fig. 2 Neural network model

wm(m=1, 2, …, 2M)是隐藏层和输出层神经元之间的相应权重，即后级权重。输入到隐藏神经元的前级权重都被固定为1。t是神经网络的输入，表示为时间，对应于采样时间点。

神经网络模型输出表示如下：

式中：pm——隐藏层神经元的激活函数。

2.1.2 确定迭代方向

与常用的监督型网络不同，这里神经网络不需要学习就能使用，并且神经网络迭代满足收敛条件后最终形成的后级权重是用来计算谐波幅值和相角的。

2.2 最优步长

3 算法步骤

基于以上算法理论，对算法步骤进行详细介绍，其算法流程如图3所示。

图3 算法流程Fig. 3 Algorithm flow

第一步：设置采样频率fs，单次准同步递归运算所用的数据量N和递归次数n。

第二步：连续采样获取[n(N-1)+1+N]个数据。按式(13)和式(14)计算准同步窗系数。按式(4)，用前[n(N-1)+1]个数据计算Fα,n(0)和Fβ,n(0)，用后[n(N-1)+1]个数据计算Fα,n(t0)和Fβ,n(t0)，此时t0等于N倍单个采样的时间。

第三步：用式(5)和式(6)估算基波频率值。

第四步：设M′=20，即神经元个数为40，并利用第三步估计的基波频率f′构造神经网络。

第五步：计算式(19)中定义的误差E。如果满足E小于误差容限、迭代后误差变化值小于设定值或d大于最大迭代次数，则进入第八步。

第六步：计算最优迭代步长，更新加权向量。

第七步：d=d+1，回到第五步。

第八步：利用最终得到的神经网络后级权向量，通过式(16)和式(17)计算各次谐波的幅值和相位。

第九步：计算结束。

4 仿真实验

为了验证本文所提算法的有效性，将其与FFT算法[9]进行对比，并进行不同基波频率下检测误差实验和不同强度白噪声下的检测误差实验，参考的标准为GB/T 14549—1993《电能质量 公用电网谐波》。

仿真时，算法设置参数如下：检测的最大谐波次数M′=20，N=51，n=4，神经网络后级部分权重初始化全为1；采样频率固定为2 560 Hz，实验均在非同步采样条件下进行，采样点数均为252。

4.1 误差对比实验

对比实验中，采用的测试信号模型为

式中：f——基波频率，f=50.1 Hz；Ai——谐波的幅值；φi——谐波的相角。

具体的谐波幅值和相角如表1所示。

表1 测试信号1谐波成分Tab. 1 Harmonic component of the first test signal

本文采用不同的算法对仿真谐波信号进行分析，其结果如表2～表4所示。可以看出，本文算法具有较高的测量精度。

表2 不同算法的基波频率相对误差Tab. 2 Fundamental frequency relative errors of different algorithms

表3 不同算法下幅值相对误差Tab. 3 Relative errors of amplitude as with different algorithms

表4 不同算法的相角相对误差Tab. 4 Relative errors of phase as with different algorithm

图4示出不同算法的误差迭代图。可以看出，该算法迭代十余次时均方误差便已极小 ，而要达到同样的效果，传统的方法[12]需经过上百次迭代。

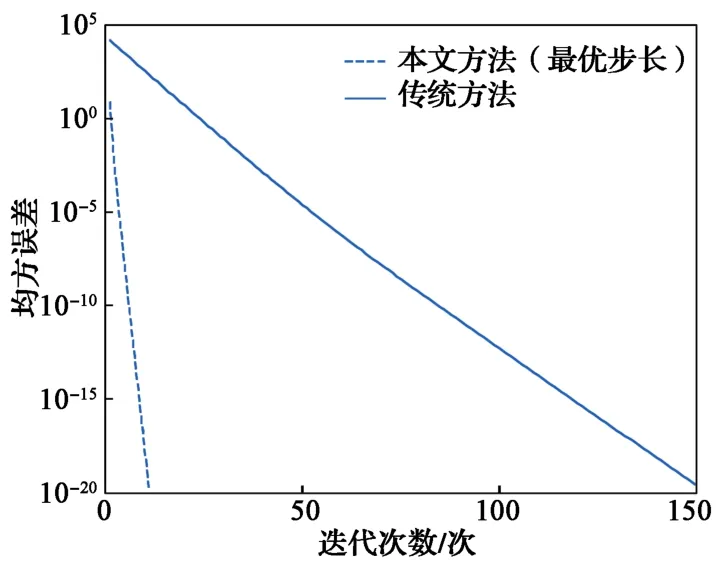
图4 随迭代变化的均方误差Fig. 4 Mean square error via iteration

从对比结果可以看出，本文算法的整次谐波分析精度非常接近于传统的基于理想基波频率的神经网络谐波分析精度（精度等级可达1×10-12），且本文算法通过最优步长的确定，极大地改善了迭代速度。

4.2 不同频率下的实验

为了验证本文算法的可靠性，在基频波动范围[49.9 Hz, 50.5 Hz]内进行谐波分析实验，谐波信号模型仍然使用表1中的数据，算法初始设置不变。频率每变化0.1 Hz，分析一次谐波信号。不同基波频率下的谐波分析结果如图5～图7所示。在算法的迭代次数方面，神经网络均在20次迭代内满足迭代终止条件。由图5～图7可知，在上述基波频率波动范围内，幅值相对误差基本在3×10-8%以内，相角相对误差基本在5×10-6%以内。值得注意的是，算法在基波频率附近，愈靠近50.2 Hz，精度愈高。这是由于采用了准同步采样算法，根据算法的初始设置，可以计算得到本文初始定义的fNs约为50.196 Hz，而准同步算法的精度一般会随着fNs靠近基波频率而提高，所以会呈现如此的结果。在实际应用中，可通过简单的测量设备测量获得低精度的基波频率作为参考量；而在一些基波频率变动范围很小的电力环境中，N和n的选择可以固定不变，这使得准同步窗系数可以提前计算，进一步改善了算法的实时性。

图5 基波频率相对误差Fig. 5 Relative error of the fundamental frequency

4.3 白噪声影响

在实践中，谐波信号分析也经常受到白噪声的影响。为了验证算法的抗干扰性能，本文进行了不同的信噪比（SNR）的仿真分析，谐波信号模型遵循表5中的数据，基波频率为50.29 Hz,算法的初始设置不进行更改，其检测结果如表6所示。从结果可以看出，本文算法在中等强度的白噪声下，仍保持一定的精度；而在算法的迭代次数方面，不同噪声强度下，均在10余次迭代后满足迭代终止条件。

表5 测试信号2谐波成分Tab. 5 Harmonic components of the second test signal

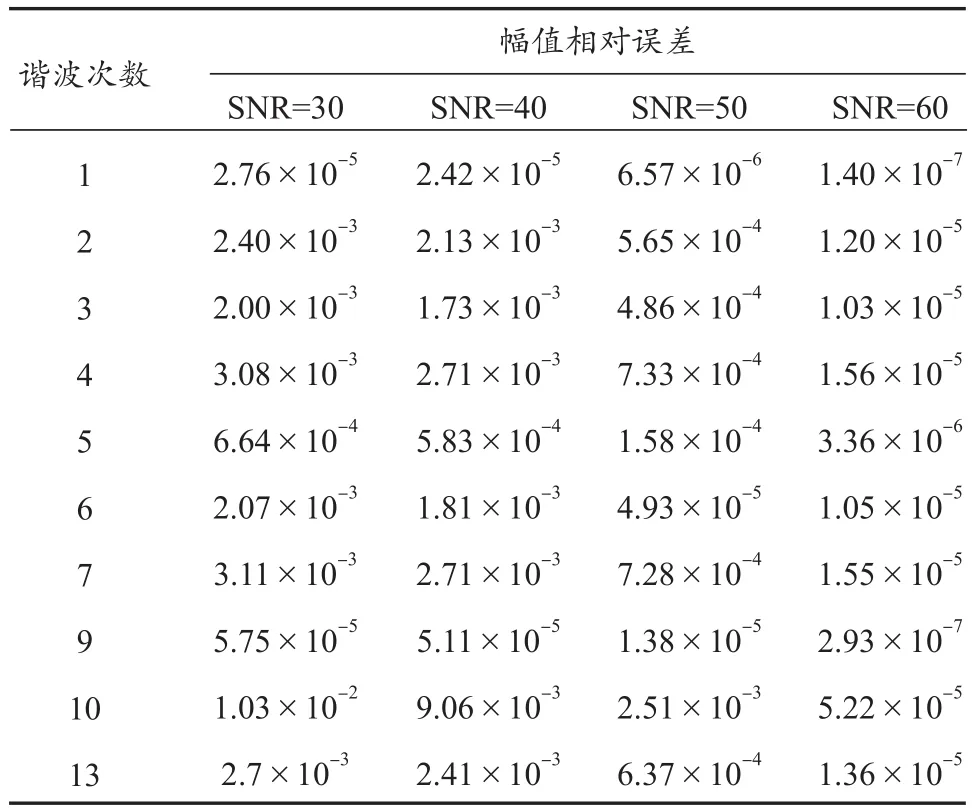
表6 白噪声影响下的幅值相对误差Tab. 6 Relative error of amplitude under the influence of white noise

5 结语

在准同步采样算法的基础上，本文首先推导了通常情况下准同步窗系数的函数表达式，以优化准同步采样算法的速度；然后以采用准同步采样算法估计的基波频率为基础，构建起神经网络谐波分析模型，确定了最速下降方向上的适应性最优步长，并论证了该步长会使神经网络收敛于全局最小值。多组非同步采样条件下的实验结果表明，本文算法精度极高，且迭代速度有了显著的改善。本文算法适用于整次谐波分析，却无法检测间谐波，这是下一步工作研究方向。