绳驱动机械手抓取力自整定模糊PID控制

管声启，张 潇，杨栋峰，肖 旭，张 超

(1.西安工程大学 机电工程学院，陕西 西安 710048；2. 绍兴市柯桥区西纺纺织产业创新研究院，浙江 绍兴 312030)

0 引 言

随着智能制造水平的提高和绿色低碳的要求，“机器换人”已成为一种必然趋势。传统纺织业正处于从劳动密集向技术密集转变的关键时期，采用机械手实现纱筒的自动化稳定抓取，将有效解决纱筒上下料对人力过度依赖的问题。本文所研究的绳驱动机械手是由SHIGEO等于1978年首次提出的，它采用类似人手肌腱收缩的驱动方式，用绳索将电机输出的驱动力传递到手指各个关节[1]。绳索张紧时，手指包络实现抓取；当驱动力消失时，手指在弹簧的作用下松开物品[2-3]。由于绳驱动机械手具有轻量化、结构简单、形状自适应能力强、对物体的包络性好等特点，被广泛应用在果蔬采摘[4]、助老机械[5-6]、残疾人辅助抓取[7-8]等领域。然而由于绳索具有线弹性形变，无法保持稳定的张紧力，导致末端执行器在抓取物体的过程中易发生震颤和滑落[9-10]。

为了减小绳索的回弹特性对控制性能的影响，国内外学者做出了诸多研究。王邢波等提出了一种绳腱驱动机械手张力约束末端操作控制方法，将绳驱动张力偏差转化为绳位置偏差，并通过绳驱动器控制腱绳的拉伸来提高末端系统操作力的控制精度[11]。王建华等将传统PID算法的力控制与前馈PID位置控制算法相结合，设计了一种控制驱动仿人肩关节的绳索张紧力大小的并行控制策略[12]。陈泉柱等采用张力传感器实时检测驱动绳索上的张力，从而对线弹性引起的张力波动进行补偿[13]。文献[14]为了提高绳驱动机械臂的位置控制精度，采用标定的方法来减小误差。汪选要等提出采用恒重力和内张力补偿的冗余绳驱动机械手控制算法，来降低绳材的弹性对控制系统的性能影响[15]。陈伟海等通过建立绳驱动仿人臂机器人的动力学方程，提出一种基于动态最小预紧力的张力分配算法，使驱动绳的张力根据动态最小预紧力实时调整[16]。这些绳索张力控制算法虽然取得了一定的效果，但是需要力和位置控制算法相结合，采用张力传感器或标定的方法来减小绳索回弹的影响，使绳驱动机械手的抓取力控制变得复杂，对线弹性形变导致的张力波动调节时间长，动态性能差。

因此，针对线弹性形变引起的绳驱动机械手实际抓取力与期望抓取力存在偏差，导致抓取目标震颤、滑落的问题，本文提出一种参数自整定模糊PID控制算法。将柔性触觉传感器置于机械手的指腹，用于感知机械手抓取目标时的实际抓握力。当绳索发生回弹导致抓握力减小时，根据触觉传感器输出的实测抓握力对其进行补偿，实现抓取目标的稳定抓取。

1 系统建模和模型降阶

1.1 绳驱动机械手系统建模

本文的控制对象是根据仿生学原理设计的欠驱动三指机械手，每个手指包含3个关节，如图1所示。

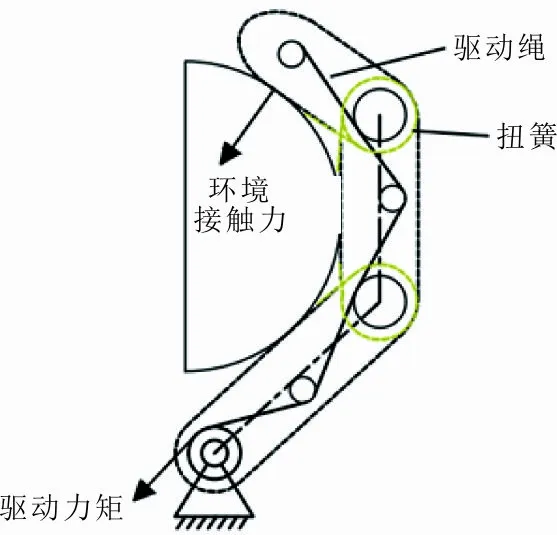
图 1 绳驱动机械手模型

欠驱动机械手的驱动源是直流电机，电机的转矩经减速后通过绳轮传动的方式转换成机械手的抓取力。为了研究欠驱动机械手的动态特性，通过式(1)建立如图1所示的机械手动力学模型[17-18]。

(1)

式中：M为系统的惯性矩阵；C为离心力和科氏力矢量；K为系统刚度；τ为系统的驱动力矩；JT为力雅可比矩阵；f为环境接触力。

环境接触力为欠驱动机械手和被抓取物体之间的接触力，可以简化为定刚度弹簧模型:

f(t)=Kex(t)

(2)

式中：Ke为环境刚度；x(t)为t时刻指腹在垂直点的位移。

假设欠驱动机械手刚与物体接触时的位置是系统的平衡位置，则位移x(t)可表示为

x(t)=lθ(t)

(3)

式中：l是手指与物体接触点到远指节旋转原点的距离;θ(t)为t时刻的关节角度。

通过式(1)、(2)、(3)可以得出：

(4)

式中:a0=m/(Kel)；a1=c/(Kel)；a2=K3/(Kel)+l。

对式(4)进行拉普拉斯变换[19]，得到电机驱动力矩到接触力之间的传递函数为

(5)

在额定的励磁下，由基尔霍夫电压定律可得直流电机电枢回路的平衡方程[20-22]为

(6)

根据式(5)和式(6)建立绳驱动机械手系统的原始模型，可表示为

(7)

1.2 数学模型降阶

控制系统的模型降阶问题是由DAVISON[23]在1967年提出的，通过模型降阶可以获得一个易于控制的阶次较小并且模型性能逼近原始系统的模型结构。由于绳驱动机械手是一个高度耦合的非线性系统，电机输入电压与指尖抓取力之间的传递函数为直流电机的一阶惯性和绳驱动机械手的二阶系统叠加而成的高阶系统，不便于控制器的设计和系统的进一步分析。因此，本文利用高维模型降阶中出现最早、十分经典和有效的Padé降阶算法[24-25]对绳驱动机械手的控制模型进行简化。Padé降阶算法的本质是利用原始系统传递函数分子、分母的系数和传递函数泰勒展开式的系数，通过对2个方程求解，得到降阶系统传递函数分子和分母的系数。

针对绳驱动机械手系统，利用Matlab编写函数来求解系统的原始模型所对应的Padé降阶模型，所得到的绳驱动机械手系统的二阶传递函数为

(8)

为了验证Padé算法的降阶效果，对降阶前后的数学模型进行时频域分析，图2为得到的阶跃响应和Bode幅频相频谱图。

(a) 阶跃响应

由时频域分析可以发现，采用Padé降阶算法降阶后的模型能够很好的逼近原始模型，简化了绳驱动机械手系统的抓取力控制算法研究。

2 自整定模糊PID控制

2.1 控制原理

绳驱动机械手抓取力控制系统的被控对象是一个非线性、时变性强的控制系统，且系统的控制性能会受到绳索回弹特性的干扰，而传统的PID控制参数固定不变[26]，难以对这种系统有效控制。因此，针对绳索发生回弹时机械手对目标抓取力减小而导致物品滑落的问题，寻找一个可以根据外部干扰对抓取力进行自适应补偿的智能控制算法是实现稳定、柔性抓取的关键。

本文将模糊控制思想与传统PID理论相结合，设计一个两输入三输出的自整定模糊PID控制器来控制抓取力。系统以绳驱动机械手指腹触觉力传感器所反馈的抓取力实测值和目标值之间的误差e和误差变化率e′作为自整定模糊PID控制器的输入变量，比例系数Kp的修正量ΔKp、积分系数Ki的修正量ΔKi、微分系数Kd的修正量ΔKd作为输出变量。e和e′经过模糊化、模糊推理和解模糊运算后得到PID参数的变化量ΔKp、ΔKi、ΔKd。利用模糊规则对PID的3个参数在线修改，然后与设定好的PID控制参数ΔKp、ΔKi、ΔKd相加，构成了抓取力自整定模糊PID控制器，其结构如图3所示。

图 3 自整定模糊PID控制器

自整定模糊PID控制器的设计是抓取力自适应控制系统的核心，决定了控制性能的优劣。

2.2 模糊语言变量及其隶属度函数的选取

针对上述问题，根据实际需求和经验，以语言变量负大NB、负中NM、负小NS、零ZO、正小PS、正中PM、正大PB作为输入变量e、e′和修正量ΔKp、ΔKi、ΔKd的模糊子集，记作{NB，NM，NS，ZO，PS，PM，PB}。在Matlab的隶属度函数编辑器中设计各语言变量对应的隶属函数相应关系，如图4所示。

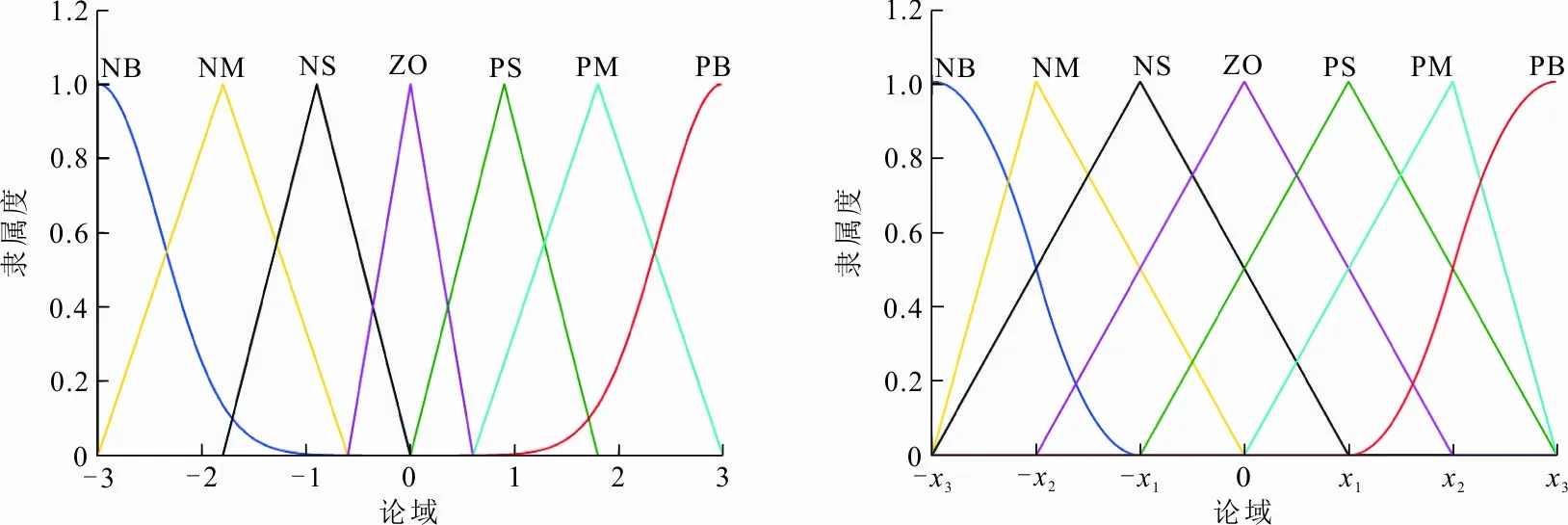
(a) e、e′的隶属函数 (b) ΔKp、ΔKi、ΔKd的隶属函数

从图4(a)可以看出，输入变量e、e′的论域为(-3，3)。其中，ΔKp的论域为(-0.3，0.3)，ΔKi的论域为(-0.06，0.06)，ΔKd的论域为(-3，3)。

2.3 模糊控制规则

模糊控制设计最核心的部分就是根据工程设计人员的技术知识和操作经验[27]，建立恰当的模糊规则表。对于本文所研究的抓取力自适应补偿控制，针对ΔKp、ΔKi、ΔKd等3个参数，分别制定如表1所示的模糊控制规则表。

表 1 ΔKp、ΔKi、ΔKd的模糊控制规则表

根据所设定的隶属函数以及各变量的论域和模糊子集，在Matlab的模糊控制工具箱中建立Mamdani型模糊控制器。以if…then…的形式输入模糊规则，选用重心法作为解模糊方法建立自整定模糊PID控制器，并将其保存为.fis格式的文件，用于后续仿真使用。

3 仿真分析

3.1 Simulink建模

本文所设计的模糊控制器为两输入单输出系统，以实测抓取力和目标抓取力的偏差e和偏差变化率e′作为输入，直流电机的输入电压作为输出，并设定相应的模糊规则建立模糊控制器。传统PID控制的控制效果受控制参数ΔKp、ΔKi、ΔKd的影响，为了获得最优控制效果，本文采用临界比例度法整定PID控制器的初始参数数值，并将其设置为模糊自整定PID控制器的初始参数。

在Matlab/Simulink环境下，建立绳驱动机械手抓取力模糊控制、传统PID控制以及自整定PID控制器仿真模型，通过直观的模块框图进行建模仿真研究。在Simulink环境下建立的抓取力控制器模型如图5所示。

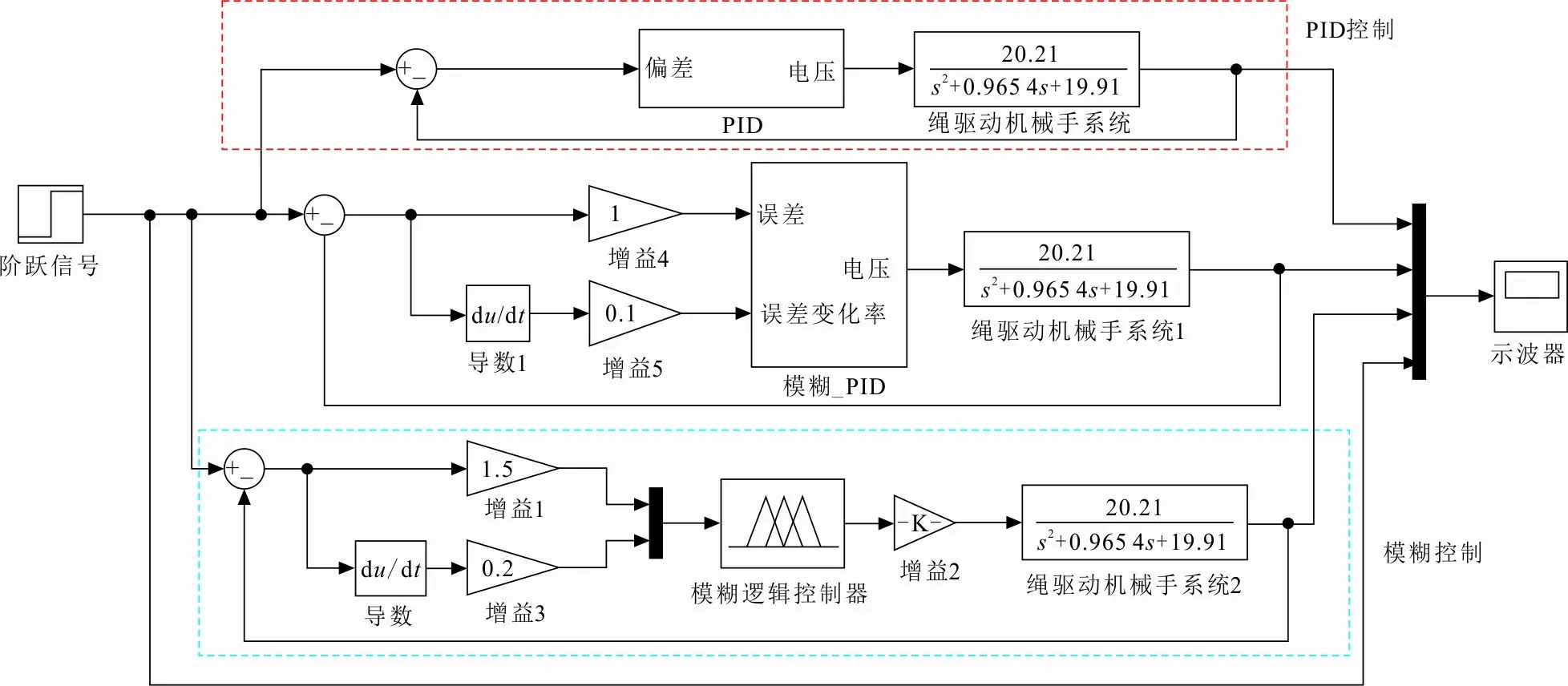
图 5 抓取力控制器模型

图5中红色方框和蓝色方框分别是PID控制和模糊控制的模块框图，而未框选部分则是本文所设计的自整定模糊PID控制模块的框图。

3.2 仿真分析

绳驱动机械手在抓取目标的过程中，为了保证效率，通常期望机械手从接触目标到实现稳定抓取的调节时间小于1 s。并且由于抓取目标的不确定性，为了避免抓取力过大导致目标损坏或抓取力不够导致目标掉落，抓取力的超调量和稳态误差应尽可能小。在系统的仿真过程中，以目标物品抓取实验过程中，抓取成功时的抓取力均值1.617 N作为理想的抓取力大小，假设系统的阶跃响应信号为1.617，获得的控制器输出响应曲线如图6所示。

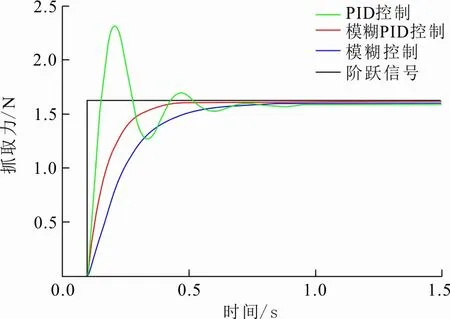
图 6 抓取力仿真

从图6可以看出，3种算法进行仿真时，最终都达到了目标抓取力。但是本文所设计的抓取力自整定模糊PID控制算法相对于其他2种算法而言，达到目标抓取力的速度更快，稳态误差大幅降低，且不会出现超调量。由图6可以得到如表2所示的抓取力响应参数。

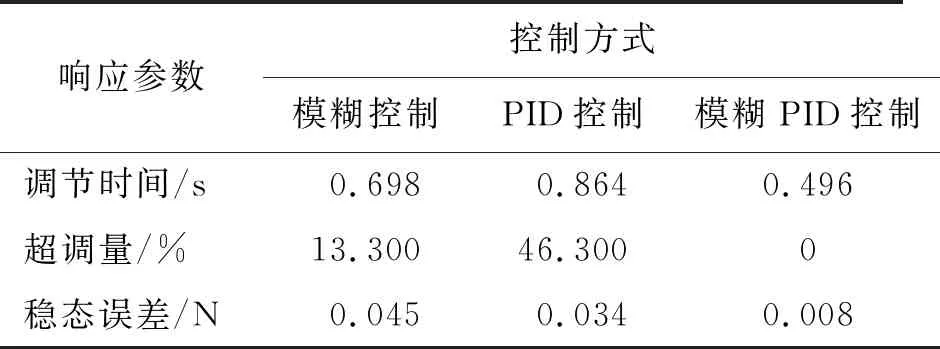
表 2 抓取力响应参数

从表2可以看出，由于本文所设计的自整定模糊PID控制器可以根据输入信号偏差e的大小、变化趋势等特征，通过模糊推理在线调整修正值ΔKp、ΔKi、ΔKd以适应控制系统的变化，所以相对于模糊控制和传统PID控制，本文所设计的自整定模糊PID控制器达到目标抓取力的时间分别缩短28%和42%，稳态误差分别减少82%和76%，超调量为0。证明自整定模糊PID控制算法能够快速、稳定的达到目标抓取力，控制效果更为理想。

为了验证本文所设计的自整定模糊PID控制算法的抓取力补偿效果，当系统运行到1.0 s时外加干扰-0.5 N模拟机械手抓取过程中由于绳索的回弹导致的传感器输出的实际抓取力减小的情况。获得的控制器输出响应曲线如图7所示。

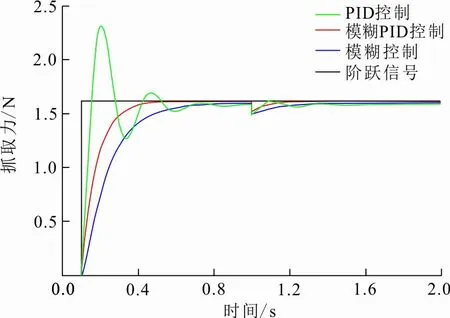
图 7 扰动仿真

从图7可以看出,由于干扰的加入，抓取力的曲线出现了明显的波动。当干扰出现后，3种算法都能根据干扰的程度迅速进行调整，使抓取力恢复到理想状态。其中，模糊控制器、PID控制器和模糊自整定PID控制器对于扰动的调整时间分别为0.366 s、0.581 s和0.276 s。通过调整时间可以看出，本文所设计的模糊PID控制器能够根据抓取力减小的程度进行迅速补偿，避免了物品滑落，保证了抓取过程中的稳定性。

4 结 语

本文设计的自整定模糊PID控制算法，实现了绳驱动机械手抓取力的自适应控制。与模糊控制和PID控制相比，自整定模糊PID控制算法在抓取力的控制过程中，调节时间分别缩短28%和42%，稳态误差分别减少82%和76%；在外加干扰的情况下，能够比其他2种算法更迅速的对抓取力进行补偿，具有更好的动态控制性能。自整定模糊PID控制算法克服了传统PID控制和模糊控制超调量大、易受干扰、响应速度慢、稳态误差大的缺点，适用于绳驱动机械手的抓取力补偿控制。