基于Deform软件二次开发和BP神经网络的TA15多向锻造微观组织预报

骆俊廷，赵静启，杨哲懿，刘卫鹏，张春祥

1.燕山大学 先进锻压成形技术与科学教育部重点实验室，秦皇岛 066004 2.燕山大学 亚稳材料制备技术与科学国家重点实验室，秦皇岛 066004

诸如航空航天、船舶制造和军事工业等领域往往要求装备具有较强的环境适应性、在复杂的条件下维持稳定工作状态，除优良的设计外，结构材料的性能也是实现这一目标的重要前提和基础。钛合金优异的耐腐蚀性、高比强度、耐高温性及无磁等特点使其脱颖而出，成为上述领域不可或缺的重要结构材料[1-3]。其中，TA15属于中等强度的近α型钛合金，力学性能均衡，被广泛应用于航空航天工业[4-5]。

合金材料的热成形过程涉及多种影响因素，而钛合金类材料又存在高温下的相变过程，微观组织演变行为复杂，传统生产方式无法实现对其成形过程中组织状况的有效掌控，容易造成废品率高、产品寿命低等问题，难以胜任于对产品性能有严格要求的各类特种装备。对于此类问题，随计算机技术发展而兴起的有限元仿真技术成为一种有效的解决手段，该技术以通过数值拟合得到的固定形式数学模型为基础，借助有限元软件实现材料热变形过程力学行为及微观组织演变行为的预测，从而为生产方案的制定及优化提供参考，其操作过程成熟易行，可有效提高生产效率[6-7]。Li等[8]采用Johnson-Cook模型构建了Ti-6Al-4V合金的流动应力本构方程，借助有限元仿真实现了合金高速加工过程中加工表面的应变、应变速率及温度演变的可靠预测。朱帅等[9]以TA15钛合金环件径轴向辗轧为研究内容，构建数学模型对各变形阶段的微观组织演变进行描述，建立宏微观耦合有限元模型，实现了变形全过程微观组织预测。但有限元仿真的准确程度受数学模型拟合精度的直接影响，而数学模型拟合所遵循的经验公式繁多，其形式固定的特点也使其难以实现复杂作用关系的完整概括。近年来，基于对人脑信息处理方式的模仿而出现的人工神经网络技术引起广泛关注，该技术具备相较有限元仿真更为优异的复杂非线性关系拟合能力，其中的BP(Back Propagation)神经网络技术应用甚为广泛，典型的3层BP神经网络可实现对任意非线性函数关系的准确逼近[10-11]。Sun等[12]利用BP神经网络技术建立了可对TA15合金热变形过程中初生α相晶粒尺寸进行预测的神经网络模型，该模型精度较高，预测误差小于5%。Li和Zhang[13]以TC11合金等温压缩变形的前α相体积分数及晶粒尺寸数据为基础，建立了前α相晶粒尺寸和体积分数的模糊神经网络预测模型，训练后的模型再结晶体积分数预测误差小于3.95%，晶粒尺寸预测误差小于2.75%，模型精度高、实用性强。神经网络技术无需选取经验公式进行数值拟合，而是直接将实验数据作为样本进行训练，进而得到预测精度较高的神经网络模型。但为保证精度，神经网络对样本数据的选取要求较高，同时其训练过程往往需要重复多次，较为烦琐，因此也存在一定局限。上述两种技术手段在钛合金研究领域均存在较为广泛的应用，但综合其各自的优缺点，相关内容仍然有待于进一步探索。

合金材料的晶粒尺寸是描述其微观组织特征的重要参数，晶粒的细化能够带来合金综合力学性能的显著提升。对于钛合金工业，现已存在循环热处理[14]和热氢处理[15]等晶粒细化手段。近年来，剧烈塑性变形技术被广泛引入钛合金产品的生产中，该类技术通过对合金施加剧烈的塑性变形实现晶粒组织的强烈细化，其中的多向锻造技术由于工艺相对简单、对设备要求较低而受到广泛关注[16-18]。有关钛合金多向锻造工艺的研究已经开展。Zhang等[19]对Ti-6Al-4V合金进行了多向等温锻造，经过3步锻造处理，合金的晶粒尺寸细化至0.5 μm，抗拉强度由894 MPa提升至1 190 MPa，延伸率自18.6%降至10.4%，并认为多向锻造过程中的动态再结晶行为导致晶粒的细化。Zhang等[20]为实现烧结态网状结构TiBw/TA15复合材料的力学性能优化，在β相转变温度下实施了多向锻造处理，使材料实现了极限抗拉强度和最大延伸率8.4%和160%的提升。但总体来看，与其他型号钛合金相比，有关TA15合金多向锻造工艺的研究还相对较少，相关工作亟待加强。

本文以TA15合金多向锻造微观组织预报为主要研究内容，分别构建合金的双相区及单相区热变形本构方程及动态再结晶模型，借助有限元仿真软件Deform的二次开发功能实现TA15合金热变形过程的仿真，另基于实验数据建立BP神经网络预测模型，对两种方法的微观组织预测结果进行分析和对比，旨在为TA15合金多向锻造工艺提供高效、准确的微观组织预报方法。

1 热压缩实验

实现材料热变形过程宏观变形及微观组织演变仿真的前提是各类数学模型的构建，典型的模型包括从宏观尺度对材料流动应力行为进行描述的热变形本构方程、从微观尺度对材料变形的动态再结晶行为进行描述的动态再结晶模型，后者又可细分为具备不同表述功能的多个模型[21-22]。构建这两类模型所需的基础数据可通过热压缩模拟实验获得，前者基于实验所得应力应变数据，而后者基于压缩后试样的微观组织分析。

1.1 实验材料

实验材料为TA15钛合金热轧棒材，其主要化学成分展示于表1。TA15合金属于近α钛合金，名义成分为Ti6Al2Zr1Mo1V，初始组织构成为α+β双相组织，如图1所示。热压缩实验所用试样为∅8 mm×12 mm的圆柱形试样。

表1 实验材料化学成分

图1 TA15初始微观组织

1.2 实验方案

钛合金存在高温下的相变过程，经测定所用TA15合金的相变点为995 ℃，当变形温度接近相变点时，组织中的α相将转变为β相，转变过程涉及能量的释放，且不同相的性能表现并不一致。因此，设定的热压缩实验包括两个温度区间：750、800、850、900 ℃为双相区热压缩实验温度区间，950、1 000、1 050 ℃为接近或超过相变点的单相区热压缩实验温度区间。热压缩实验在Gleeble-1500热压缩实验机上进行，压缩的应变速率为0.001、0.010、0.100、1.000 s-1，实际操作时以2.5 ℃/s 的速度将试样加热至设定温度并保温3 min，随后进行压缩量为60%的热压缩实验，变形结束后立即水冷以保留变形组织。

1.3 实验结果与分析

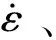
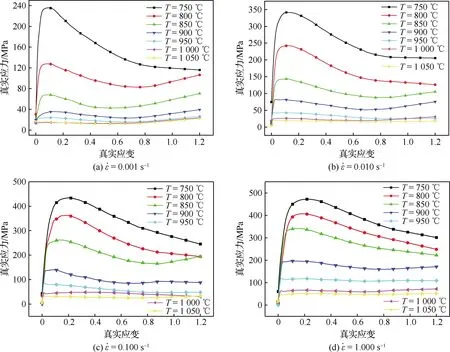
图2 相同应变速率不同变形温度下的真应力-应变曲线

图2中曲线显示TA15合金在热压缩过程中存在明显的动态再结晶特征，对压缩后试样的微观组织进行观察与分析，统计得到如表2所示包括动态再结晶体积分数Xdrx和动态再结晶晶粒尺寸Ddrx的再结晶数据，这些数据是进行相关数学模型构建的重要基础。

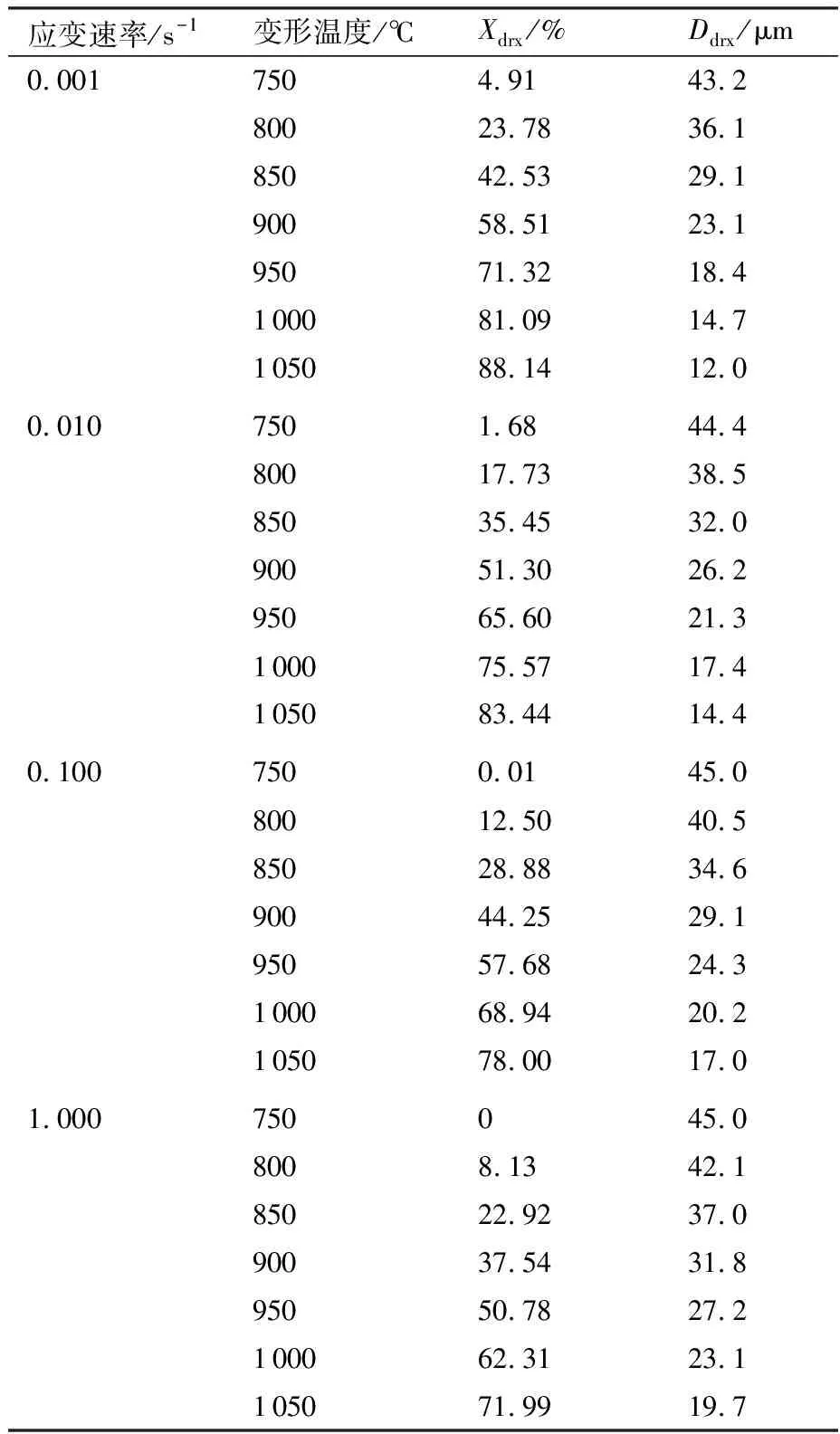
表2 热压缩试样动态再结晶数据

2 TA15合金多向锻造有限元仿真

2.1 相关数学模型

热压缩曲线显示TA15合金在双相区和单相区温度区间内具有截然不同的流动应力特性，单一本构方程无法准确描述，因此根据不同温度区间的流动应力特性推导了相对应的热变形本构方程，方程按Arrenhenius模型中的双曲正弦模型建立。

双相区曲线具有明显动态再结晶特征，取得如表3所示各变形条件下的峰值应力作为构建基础，建立的峰值应力本构方程为

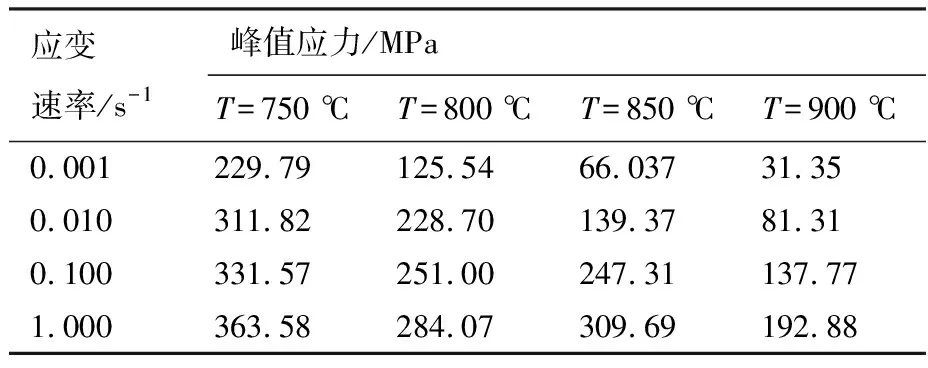
表3 双相区各变形条件下的峰值应力

(1)

式中：σp为峰值应力，MPa；R为气体常数，R=8.314 J·(mol·K)-1；T为变形温度，℃。

对于单相区曲线，其峰值应力后的软化行为不明显，峰值应力与稳态应力接近，因此采用如表4 所示的合金塑性变形阶段的流动应力均值作为方程的构建基础，建立的本构方程为

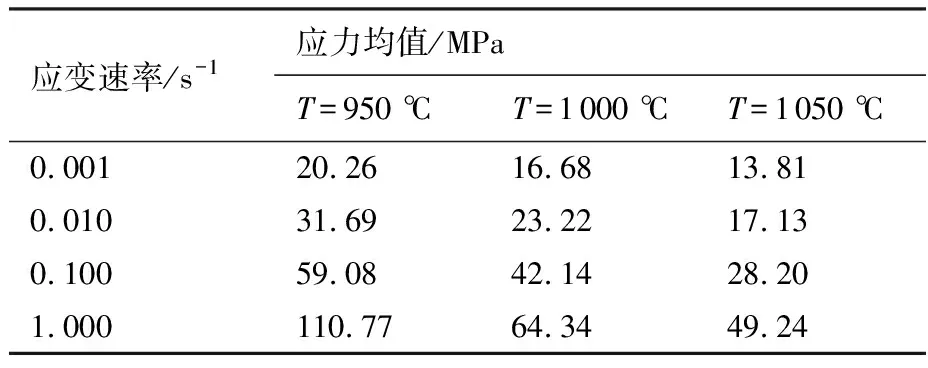
表4 单相区各变形条件下的流动应力均值

(2)

根据表2中的再结晶数据，建立了如式(3)～式(5)所示的动态再结晶模型，依次为动态再结晶临界应变模型、动态再结晶体积分数模型以及动态再结晶晶粒尺寸模型：

(3)

(4)

(5)

式中：εp为峰值应变；εc为临界应变；Xdrx为动态再结晶体积分数；ε为应变量；ε0.5为动态再结晶体积分数为50%时的应变。

动态再结晶后组织的平均晶粒尺寸称为动态再结晶平均晶粒尺寸(Davg)：

Davg=DdrxXdrx+D0(1-Xdrx)

(6)

式中：D0为初始晶粒尺寸。

2.2 Deform二次开发

有限元仿真软件Deform能实现对金属材料成形过程宏观变形及微观组织演变行为的仿真，并提供前处理和后处理两种二次开发手段，用户可借此实现自定义模型的导入。在前处理阶段对自定义子程序进行了编译，将TA15双相区和单相区热变形本构方程写入，以此实现对材料属性的定义，开发流程如图3所示。在后处理阶段，可通过对有限元计算结果文件的处理获得相关组织演变信息，将包括动态再结晶临界条件模型、动态再结晶体积分数及晶粒尺寸模型在内的动态再结晶模型编译进脚本文件，将其链接至动态链接库文件，即可在后处理界面通过调用该库实现自定义变量的显示，开发流程如图4所示。

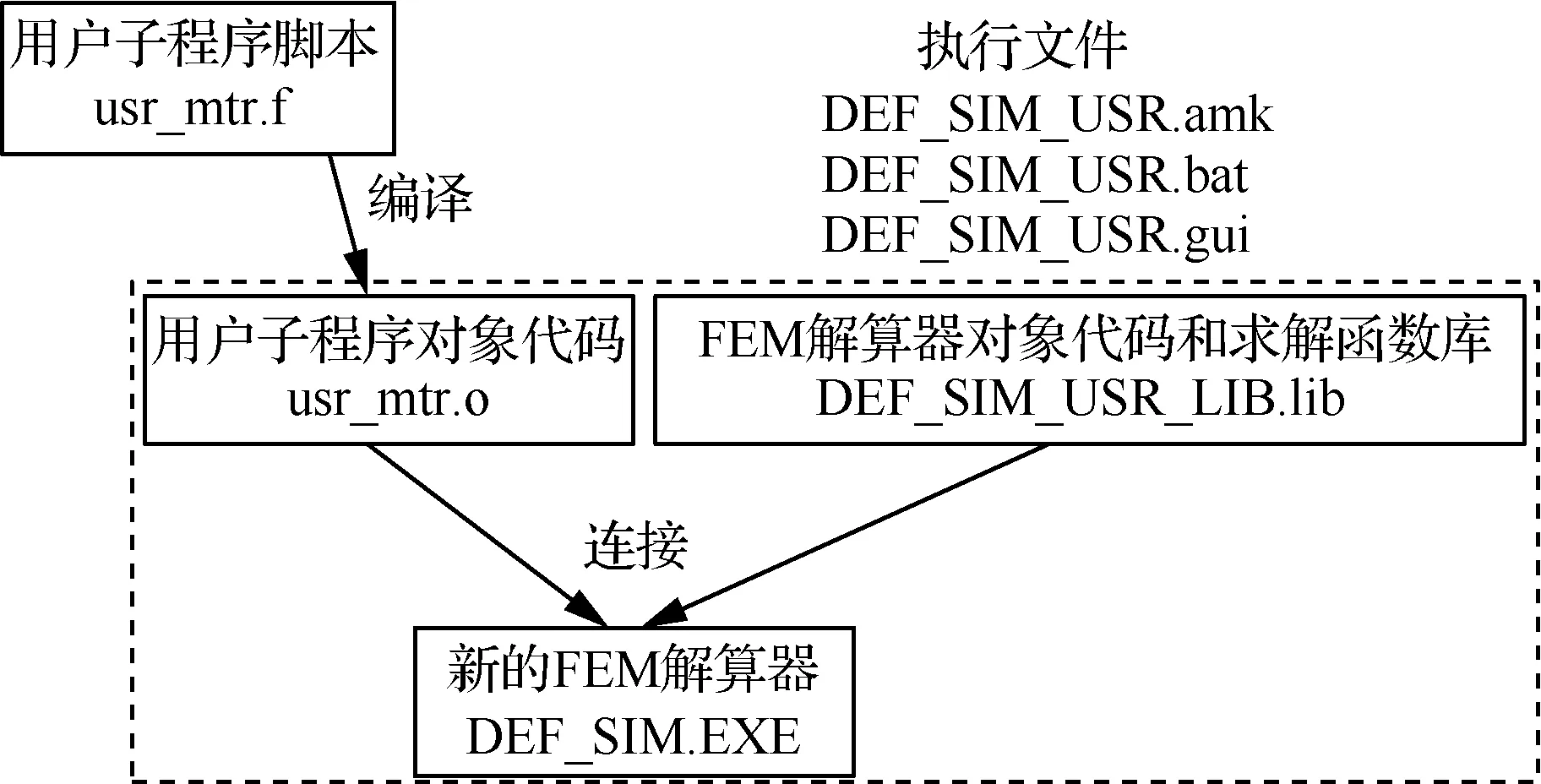
图3 前处理二次开发示意图

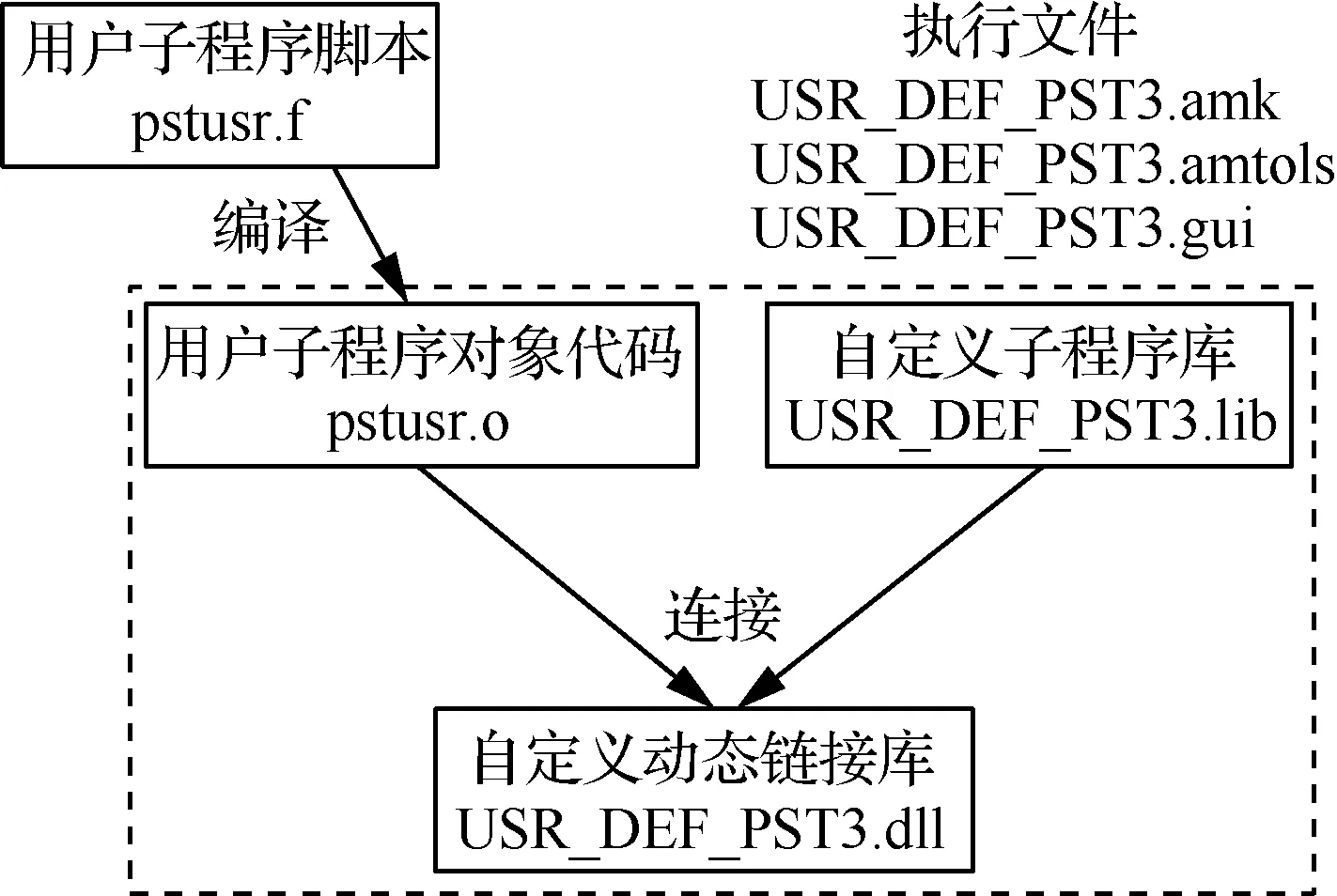
图4 后处理二次开发示意图

2.3 有限元模型的建立

多向锻造工艺通过加载方向的变换和加工道次的累加实现材料的剧烈塑性变形，促使材料发生动态再结晶，实现其微观组织的细化，进而达到提升宏观力学性能的目的[23]。经过长时间发展，多向锻造工艺扩展出多向自由锻、多向模锻和多向挤压工艺，区别在于加工的方式，但在原理上仍保持一致。研究内容为TA15合金的等温多向模锻，具体采用的工艺按模具结构不同分为闭式多向锻造、双开式多向锻造和单开式多向锻造。

首先构建出坯料及3种多向锻造模具的几何模型，选用四节点四面体单元将坯料划分成25 000个 四面体单元；将模具与坯料间的接触定义为刚体-柔性体接触，摩擦属性选用剪切摩擦，摩擦因数设置为0.3，最终得到如图5(a)～图5(c)所示的有限元模型，图5(d)展示了在后处理阶段进行自定义变量提取时采用的截面方式。

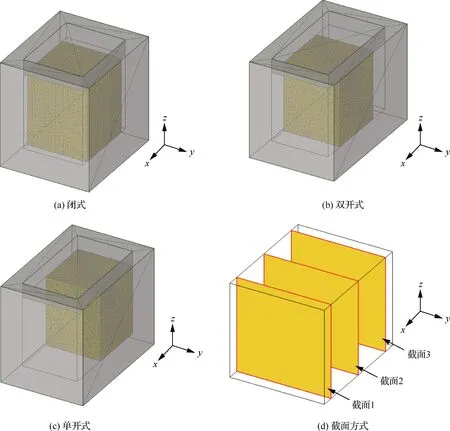
图5 有限元模型

闭式和双开式多向锻造工艺的坯料初始位置为模具型腔几何中心，而单开式多向锻造的坯料则放置于型腔的一侧。坯料在高度方向(Z)上发生压缩变形，在长度方向(X)上发生拉伸变形，在宽度方向上(Y)受模具约束而不发生变形。将每一次达到预设压下率的加载定义为一道次变形，每道次变形结束后，将闭式及双开式的坯料分别沿X和Y方向翻转，从而对其施加另一方向的下一道次变形，而在单开式各道次变形结束后，将坯料依次沿X、Y和Z方向进行翻转，并如此循环，从而实现坯料的均匀变形。对于多向锻造过程，采用不同的模具结构，坯料的应力状态存在明显差异，并将最终体现于微观组织状态，除此之外材料多向锻造过程的主要影响因子还包括变形温度、应变速率以及单道次压下率。为提高工作效率，采用L9(34)型正交表进行实验设计。由于TA15合金的相变特性，故依相变温度点划分为双相区和单相区仿真，即按照两种材料的形式进行，表5所示为双相区仿真正交表，单向区仿真在此基础上将温度水平取值变为950、1 000、1 050 ℃。表5 中的C表示闭式模具，B表示双开式模具，S表示单开式模具，每组工艺均进行9道次变形。为保证坯料每道次变形后的尺寸与之前一致，在设计坯料时，使其高度尺寸比长度尺寸多出一个单道次压下率的量，对于不同单道次压下率(20%、30%和40%)，设计的长方体锻造坯料的尺寸分别为40 mm×40 mm×50 mm、35 mm×35 mm ×50 mm和30 mm×30 mm×50 mm。材料初始晶粒尺寸设定为45 μm。

表5 双相区有限元仿真正交表

Table 5 Orthogonal table for finite element simulation of

dual-phase region

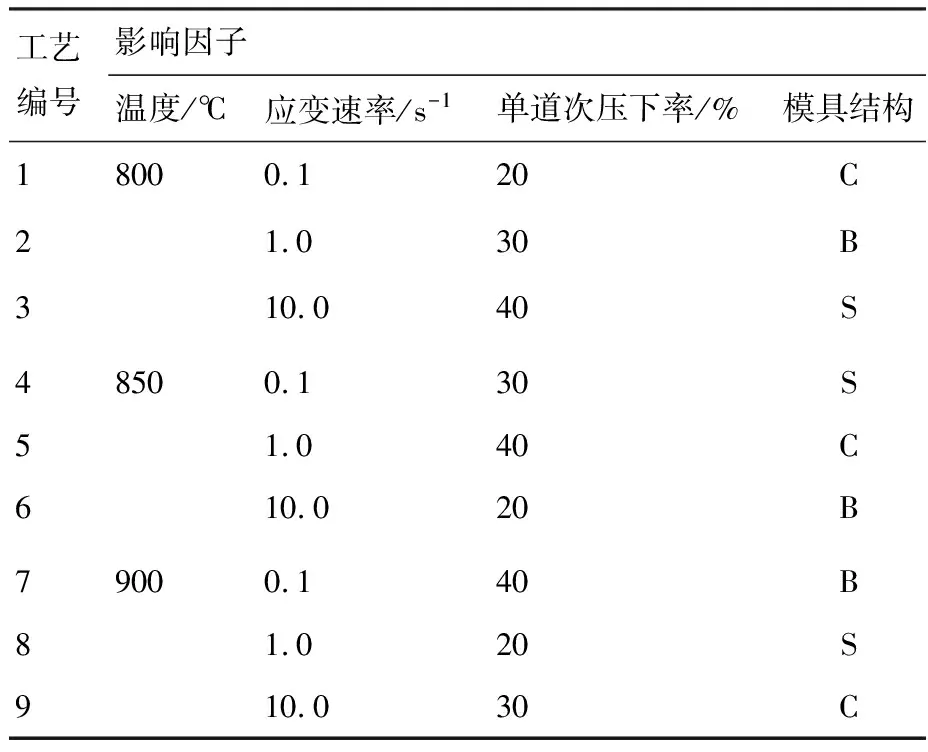
工艺编号影响因子温度/℃应变速率/s-1单道次压下率/%模具结构18000.120C21.030B310.040S48500.130S51.040C610.020B79000.140B81.020S910.030C

2.4 双相区仿真结果与分析

以工艺1、工艺2和工艺3为例，对双相区多向锻造仿真结果进行简要概述。

工艺1的有限元仿真结果如图6所示，工艺1采用闭式模具，在800 ℃的工艺分组中具有最低的应变速率和单道次压下率。随着道次累加，坯料最终的再结晶体积分数达到96%以上，如截面所示，坯料心部实现完全动态再结晶，外表面区域的再结晶程度稍低；对于晶粒尺寸，随道次累加坯料的晶粒尺寸逐步发生明显的细化，最终的整体晶粒尺寸均值约为10.3 μm，坯料心部及棱边为细小晶粒区域，而外表面处的晶粒尺寸稍大，此状态与再结晶分布相对应；由于采用闭式模具且应变速率及压下率较低，变形过程中坯料的形状保持良好。

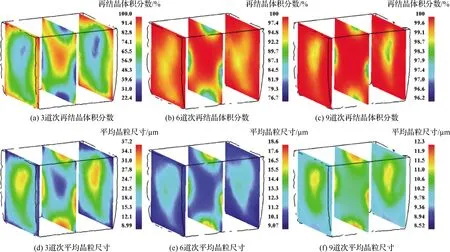
图6 双相区工艺1仿真结果

工艺2的有限元仿真结果如图7所示，工艺2采用双开式模具，其应变速率及单道次压下率相比工艺1有所提高。云图显示，坯料在3道次变形后即已实现大部分区域的完全动态再结晶，6道次后坯料整体的再结晶体积分数已达99.3%以上，9道次后实现整体完全动态再结晶；随道次累加，坯料晶粒尺寸细化明显，最终均值约为9.56 μm，但分布不均匀，对于不同的截面，较大尺寸晶粒的分布位置存在差异，且无明显分布规律；由于采用双开式模具且压下率增大，坯料长边两端产生较大宏观形变，容易在后续变形发生失稳，影响锻造效果。鉴于工艺2相对于工艺1参数的改变及仿真结果的差异，认为应变速率及单道次压下率对合金再结晶行为影响较大。

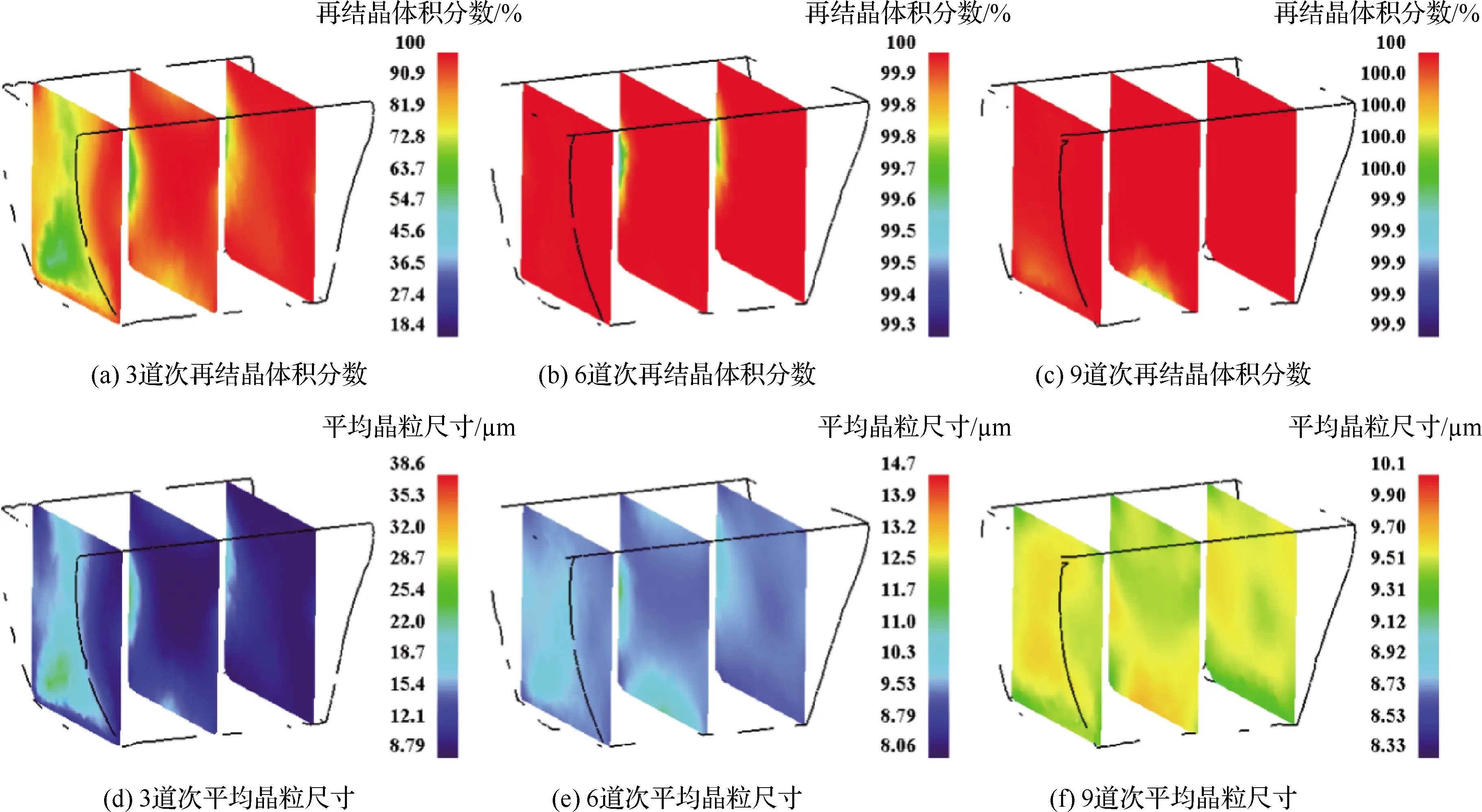
图7 双相区工艺2仿真结果

图8展示了工艺3的仿真结果，工艺3采用单开式模具，应变速率及单道次压下率均达到最大。云图显示，3道次变形后，再结晶体积分数在坯料截面上呈对角线分布，越靠近坯料长边右侧再结晶程度越高，认为这与单开式的模具结构有关，随着道次累加坯料的再结晶程度加深，9道次变形后，动态再结晶程度达100%；与再结晶体积分数的分布状态一致，低道次时坯料截面上的晶粒尺寸呈对角线分布，9道次变形结束后，尺寸均值约为8.69 μm，坯料心部的尺寸稍大，细晶粒分布于坯料左下及右上的棱边区域；因采用单开式模具且压下率较大，坯料长边左侧出现较大宏观形变。

图8 双相区工艺3仿真结果

由于在各组工艺条件下均可实现坯料的完全动态再结晶，认为该型合金属于易发生动态再结晶的材料，故不再对影响因子与动态再结晶体积分数间的关系进行讨论。表6为各组工艺条件下坯料的平均晶粒尺寸仿真结果，为对各项因子的影响进行定量、严谨的分析，以3道次、6道次和9

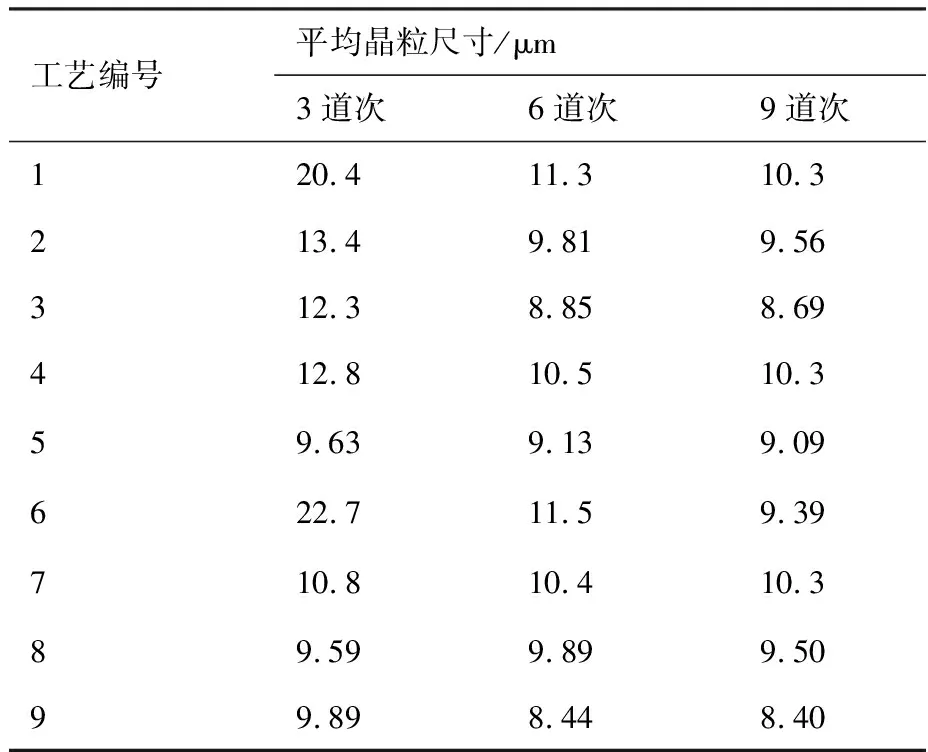
表6 双相区仿真结果统计

道次锻造变形后的平均晶粒尺寸为研究指标，计算出各项因子不同取值对应指标的平均值和极差，结果如表7所示。

通过观察可以发现，对于不同的变形道次，各因子取值的影响大小并非一成不变：对于3道次和6道次变形，单道次压下率不同取值对应指标的均值表现出最大的极差，表明在这两个阶段单道次压下率的取值对坯料的平均晶粒尺寸影响较大，但对于9道次变形，单道次压下率并不具有最大极差，表明其取值对后期变形的影响减弱；变形温度取值对应指标的均值极差显示，其取值在前3道次变形中有较强影响，但在后续道次中均处于最低影响水平；随着道次的累加，应变速率取值的影响逐渐提升至首要地位；数据显示，在道次累加的变形过程中，模具结构对晶粒尺寸指标的影响整体处于中下级水平。

表7中数据进一步显示：对于3道次变形结果，平均晶粒尺寸数值随变形温度和单道次压下率的提高而减小，随应变速率的提高而先减小后增大，晶粒细化的最佳组合为900 ℃-1.0 s-1-40%；累加至6道次变形，平均晶粒尺寸随应变速率和单道次压下率的提高而减小，随变形温度的提高而先增大后减小，但极值显示无论减小还是增大的幅度均低于3道次变形后的状况，最佳组合为900 ℃-1.0 s-1/10.0 s-1-40%；对于9道次变形后的结果，平均晶粒尺寸随应变速率和单道次压下率的提高而减小，随变形温度的提高而先增大后减小，但极值显示这种变化的幅度进一步下降，说明随着变形道次增加，各因子取值的变化对晶粒尺寸的影响会减弱，最佳组合为900 ℃-10.0 s-1-40%；坯料的平均晶粒尺寸在3道次变形后相对初始状态有大幅下降，6道次后的尺寸相比于3道次有小幅降低，但9道次后的尺寸相比于6道次几无变化，这表明多向锻造对于TA15晶粒尺寸的细化存在一定限度；使用单开式模具的坯料在3道次变形后具有最小晶粒尺寸，而6道次和9道次变形后，使用闭式模具的坯料具有最小的晶粒尺寸。结合仿真云图可以发现，受结构影响，使用单开式和双开式模具变形的坯料的晶粒尺寸存在不对称、不均匀分布的现象，且易发生局部的较大宏观形变。因此，使用闭式模具进行TA15合金的双相区多向锻造变形效果较好。

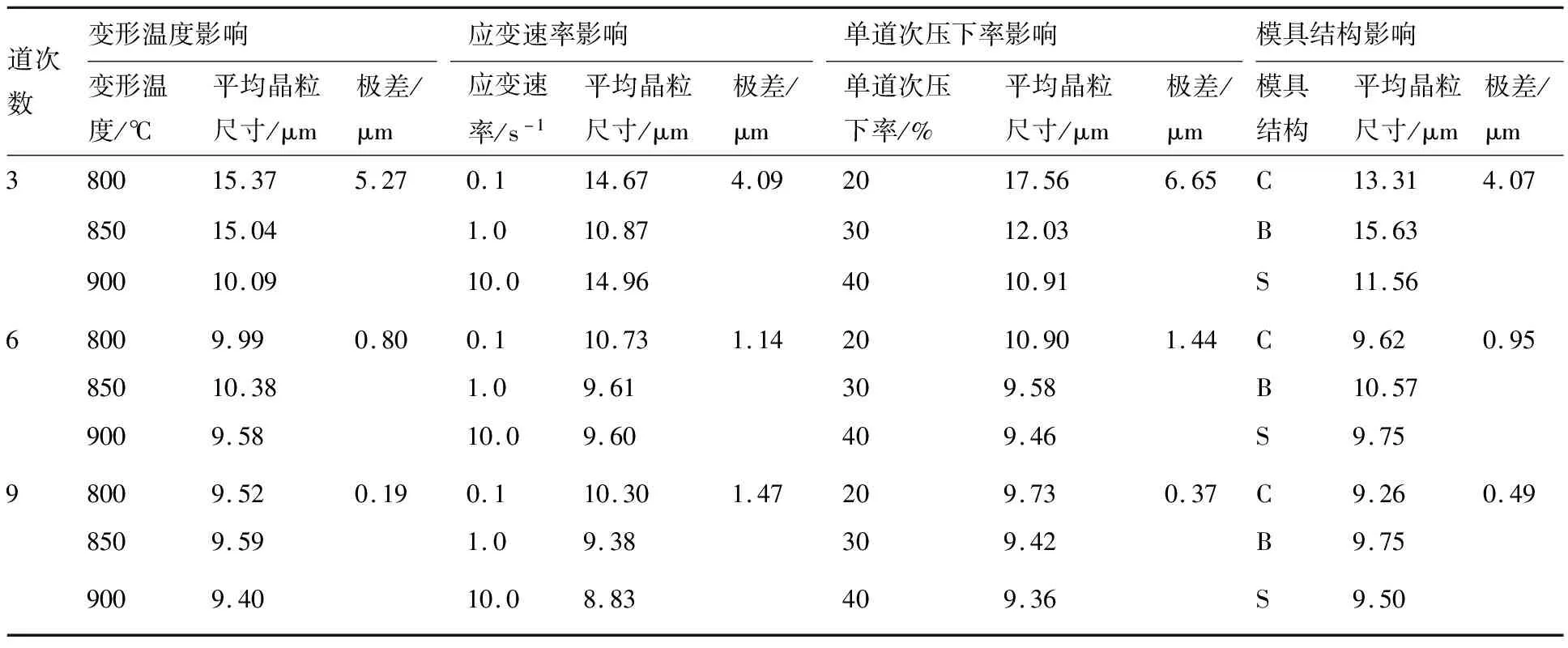
表7 双相区正交实验数据处理

通过正交实验分析提出了不同道次分组的最佳因子组合，考虑到高道次变形时各因子取值的变化对于晶粒尺寸的影响程度有所减弱，最终提出TA15合金双相区温度区间内多向锻造变形的最佳条件：以进行9道次变形为标准，最佳因子组合为900 ℃-10.0 s-1-40%-C。

2.5 单相区仿真结果与分析

以工艺1、工艺2和工艺3为例，对单相区的多向锻造仿真结果进行简要概述。

图9所示为工艺1的仿真结果，相比于800 ℃时的双相区变形，坯料经6道次后即基本实现完全动态再结晶；对于晶粒尺寸，3道次变形后的细化程度明显高于双相区变形，但后续变形的细化幅度降低，且最终数值与双相区基本接近；经3道次和9道次变形后，坯料心部及边角处分布有小尺寸晶粒，而外表面区域的晶粒尺寸稍高，整体分布状况与双相区类似，具有对称性，但经9道次变形后，坯料中段截面的中心显示了较大尺寸晶粒的存在，表明晶粒尺寸均匀性略有下降。

图9 单相区工艺1仿真结果

工艺2的仿真结果如图10所示，相比于工艺1，工艺2更大的单道次压下率及较高的应变速率明显促进了再结晶的进行，但最终的晶粒尺寸均值约为9.55 μm，与工艺1的结果接近；9道次截面显示，坯料下表面区域的晶粒尺寸较小，其余位置尺寸稍高，整体上的晶粒尺寸分布虽不具有对称性，但较为均匀一致；由于采用双开式模具且压下率增大，坯料长边的两端产生较大宏观形变，容易在后续变形造成失稳。

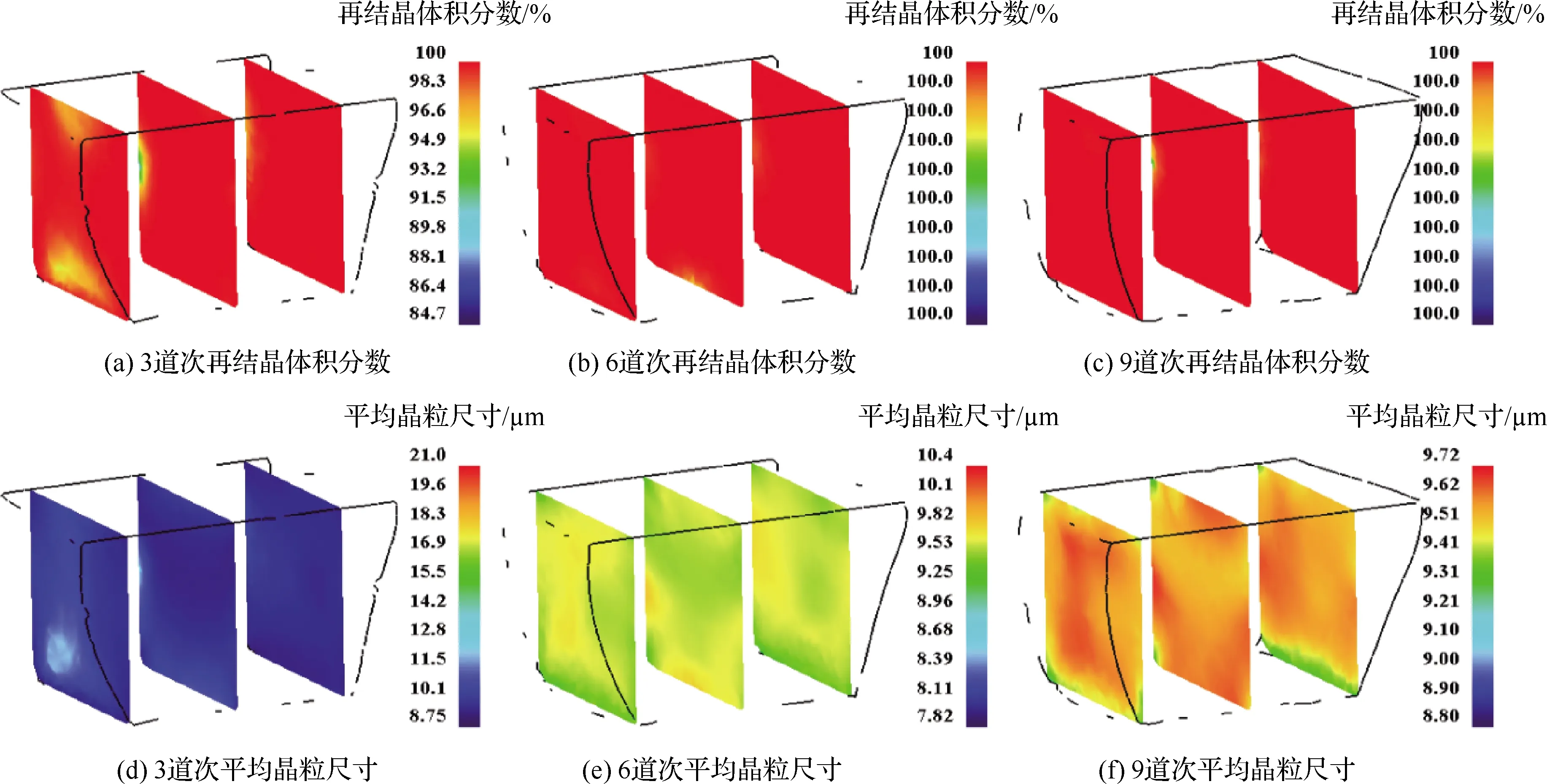
图10 单相区工艺2仿真结果

图11展示了工艺3的仿真结果，坯料在工艺条件3下经6道次变形即可实现完全动态再结晶，受应变速率及单道次压下率提高的影响，晶粒尺寸的细化程度相较前两组工艺有所提高，最终的晶粒尺寸均值约为8.62 μm。工艺3采用单开式模具，晶粒尺寸的分布状况也有所改变：截面上的左半部分晶粒尺寸稍高，而右半部分尺寸稍低；整体上，受模具影响，坯料长边右端的晶粒尺寸较低，而左端的尺寸稍高且宏观上发生较大形变。

图11 单相区工艺3仿真结果

各组工艺条件下坯料的平均晶粒尺寸仿真结果列于表8，正交实验数据的处理结果如表9所示。单道次压下率对于3道次变形结果影响较大，但对后续道次的影响逐渐减弱；模具结构对晶粒尺寸存在中等影响，但认为其主要影响晶粒尺寸的分布；变形温度对晶粒尺寸的影响程度随着变形道次的增加而减弱，对于6道次及9道次变形，其影响始终处于最低水平；与其他因子状况不同的是，随着道次累加，应变速率升至主要影响地位。单相区各因子影响地位的变化情况与双相区差异较小，但各因子表现的极差数值相比双相区有大幅缩减，说明各因子取值变化对坯料晶粒尺寸的影响程度下降，结合图2的分析认为相变的发生和较高的温度条件导致了这一现象。

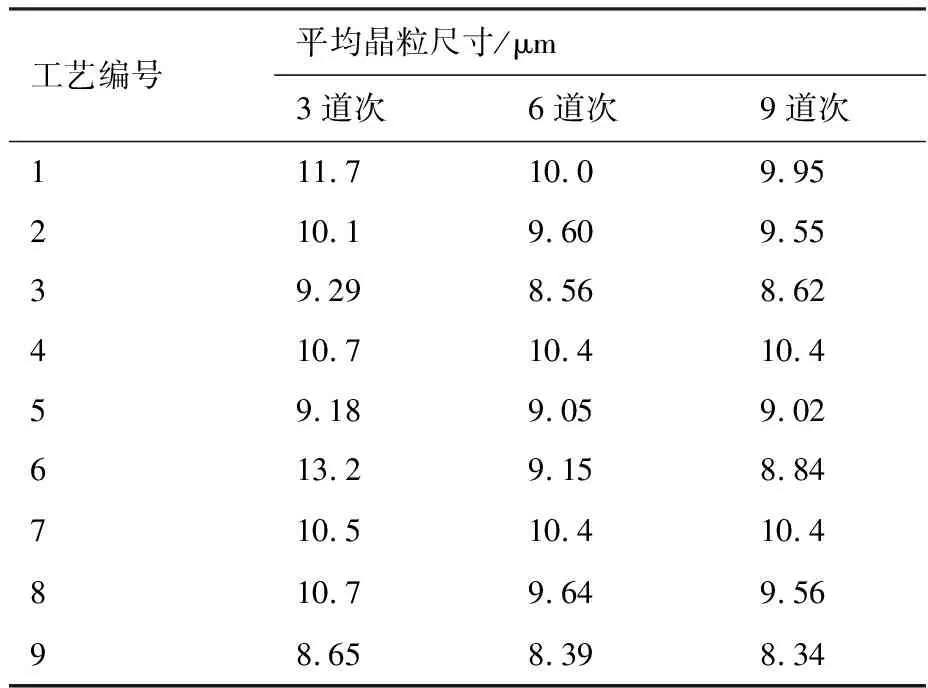
表8 单相区仿真结果统计

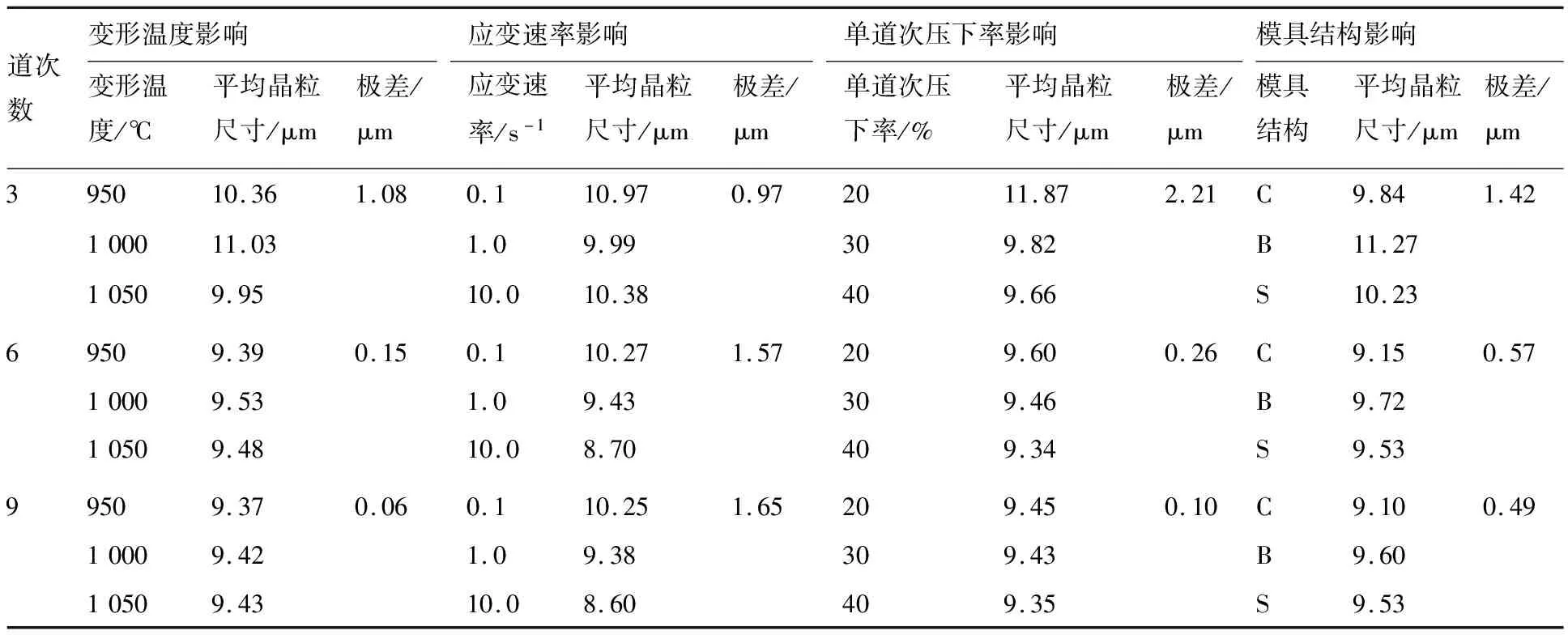
表9 单相区正交实验数据处理

对于3道次、6道次和9道次变形，晶粒尺寸随各项因子不同取值的变化情况与双相区基本一致，且随着变形道次的累加，各因子取值变化的影响程度整体呈下降趋势，晶粒的细化幅度也逐渐放缓。在模具结构方面，使用闭式模具变形的坯料在所述道次变形后均具有最低的平均晶粒尺寸，同时考虑到坯料变形的稳定性，认为使用闭式模具进行TA15合金的单相区多向锻造变形效果较好。经过综合考虑，以进行9道次变形为标准，认为TA15合金单相区多向锻造变形的最佳因子组合为1 050 ℃-10.0 s-1-40%-C。

3 基于BP神经网络的TA15合金多向锻造微观组织预报

3.1 神经网络建模

典型的BP神经网络包括3个网络层：输入层、隐含层和输出层，通过对有限元仿真结果进行分析讨论，认为各项因子的影响对象及影响强弱存在差异。在此基础上，以变形温度、应变速率和真应变为输入层，动态再结晶体积分数和动态再结晶平均晶粒尺寸为输出层，建立了直接影响再结晶的神经网络模型；以变形道次、模具结构及单道次压下率为输入层，真应变为输出层，建立了直接影响应变分布的神经网络模型。借助式(7)计算得到两种模型的隐含层神经元个数，确定的个数范围分别为3～12和2～12。

(7)

式中：num代表隐含层神经元个数；m为输入层节点个数；n为输出层节点个数；a为常数。

节点传递函数是神经元权值的传递媒介，而人工神经元的连接强度与权值呈正相关，因此传递函数的选择对于神经网络的拟合精度尤为重要。基于MATLAB神经网络拟合工具箱，在隐含层使用式(8)所示的Sigmoid函数，输出层使用式(9)所示线性函数，给定不同的神经元节点个数，进而实现函数拟合。

(8)

y=x

(9)

综上所述，最终建立了如图12所示的神经网络拓扑结构。

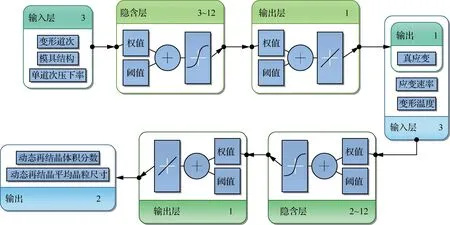
图12 神经网络拓扑结构

借助神经网络拟合工具箱对构建的BP神经网络进行多次训练和反复调整，图13展示了关于动态再结晶平均晶粒尺寸的网络模型最终训练后的线性回归拟合图，训练集(Training)、确认集(Validation)以及测试集(Test)的拟合结果均显示其输出值与目标值存在0.99以上的相关性，各点离散程度较低，表明该模型已具有较高精度和较强的泛化能力，可用于对象材料的微观组织预测。

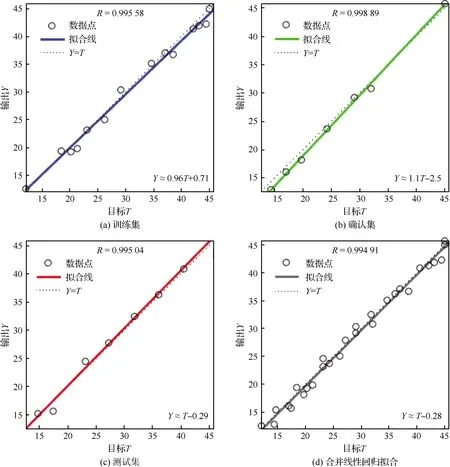
图13 最终训练后的线性回归拟合图

3.2 神经网络预测结果与讨论

利用MATLAB提供的图形用户界面开发功能(Graphical User Interface，GUI)将训练后的神经网络编写为可执行函数，并与有限元仿真一同纳入TA15合金多向锻造微观组织预测模块。在保证温度范围跨越相变点的前提下随机选定如表10 所示的多向锻造条件，分别进行有限元仿真和神经网络预测，预测结果以3组切片的形式展现，内容包括动态再结晶体积分数和动态再结晶平均晶粒尺寸数据。

表10 实验条件

图14～图16对比展示了两种不同预测方法对各实验分组的预测结果，以各分组坯料的切片1为例，对预测结果进行分析。

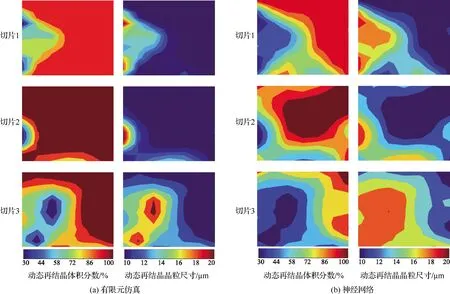
图14 分组1结果对比

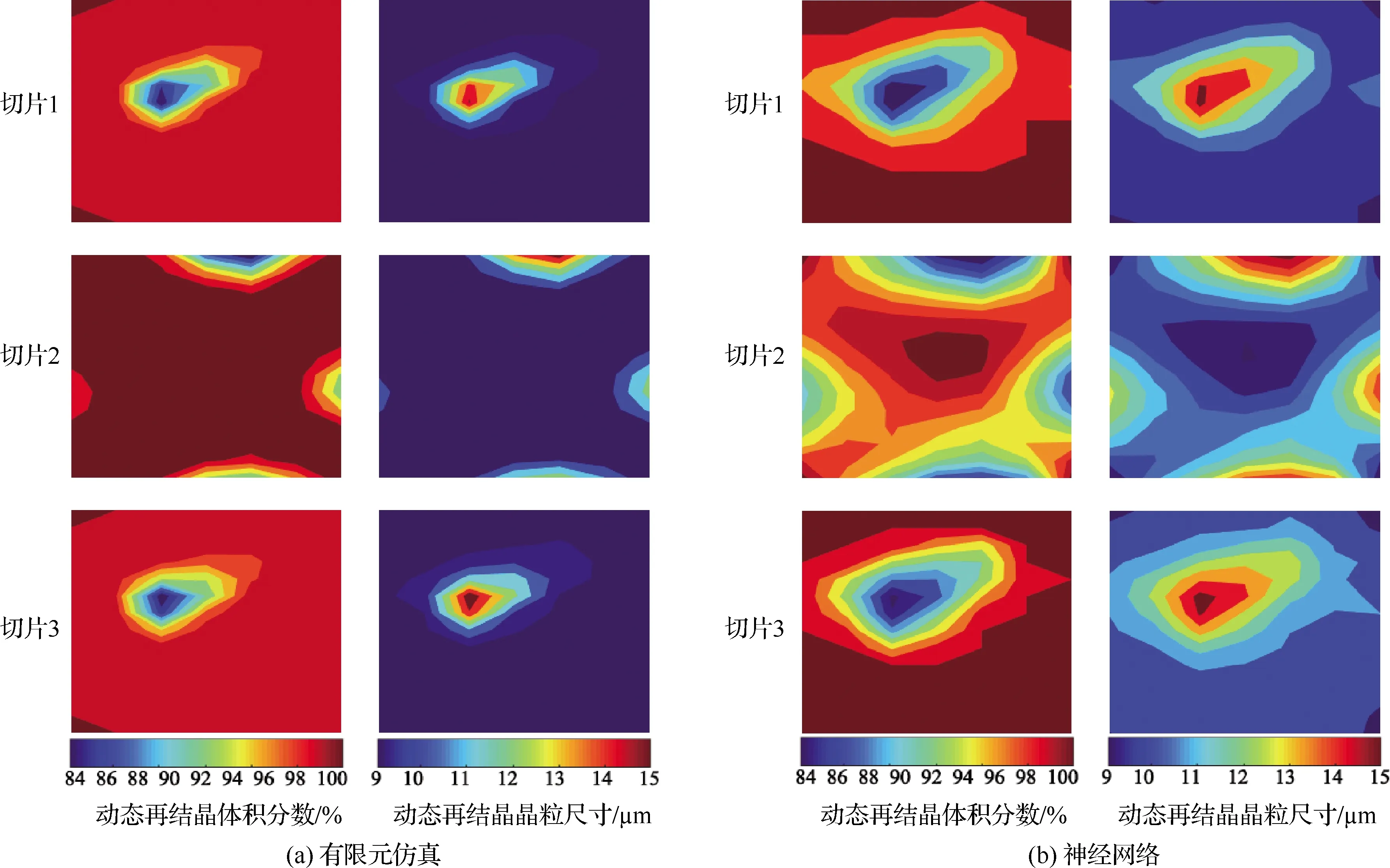
图15 分组2结果对比

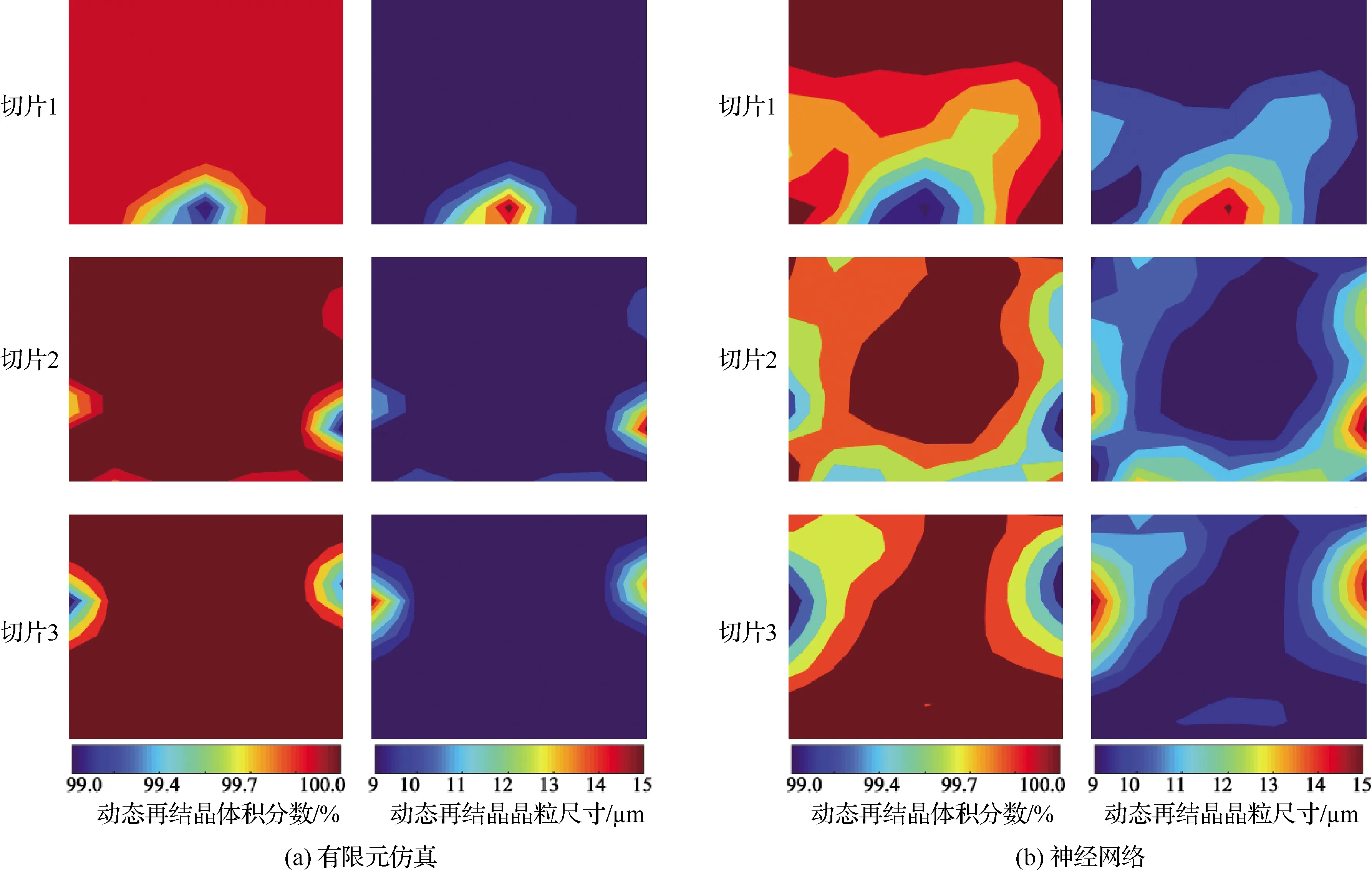
图16 分组3结果对比

1)分组1

有限元仿真结果显示，高动态再结晶程度区域占据切片中间及右侧共80%左右的面积，再结晶体积分数最高值为90%，切片1左侧分布有小面积低动态再结晶程度区域，体积分数最低值为30%；神经网络预测的切片1再结晶体积分数最低值及最高值与有限元仿真结果一致，切片1的左侧同样为低再结晶程度区域，但再结晶体积分数达到90%的区域只占据切片右上角约45%的面积，在有限元仿真中呈现高再结晶程度的切片中间及下方区域在这里显示出更细致的体积分数划分，由切片1左侧低再结晶程度区域至右上角高再结晶程度区域的体积分数过渡分层达6层，同时在切片下方还显示了小面积的不同再结晶体积分数的划分，整体表现出的细节更加丰富；两种方法预测的切片1动态再结晶晶粒尺寸分布状态与各自再结晶体积分数的分布状态一致，且得到的晶粒尺寸最低值和最高值相同，同样，神经网络预测结果对于晶粒尺寸分布的划分更为细致，细节丰富。

2)分组2

两种方法关于切片1动态再结晶体积分数及动态再结晶晶粒尺寸数据的预测结果一致，最高值及最低值相同；两种预测结果均显示，切片1中间偏左上的位置为低再结晶程度区域，对应的动态再结晶晶粒尺寸也偏高；同样，神经网络预测结果对于原本在有限元仿真结果中呈现单一体积分数的大面积高再结晶程度区域的表达展现出更加细致的划分，高、低再结晶程度区域之间存在较多过渡分层，而再结晶晶粒尺寸的预测结果存在相同表现。

3)分组3

两种预测结果均显示切片1的下方存在小面积低再结晶程度区域，而余下约90%的面积表现出较高动态再结晶程度，不同的是，有限元仿真将高再结晶程度区域整体显示为99.8%的再结晶体积分数，而神经网络则在相同区域上表达出由99.7%至100.0%的逐渐过渡分层状态；两种预测方法得到的动态再结晶晶粒尺寸的最高值和最低值相同，而具体的分布状态与各自的动态再结晶体积分数的分布状态一致，神经网络预测结果对于晶粒尺寸分布的划分更为细致。

各实验分组坯料其余切片的预测结果也表现出相同状态，有限元仿真以通过数值拟合得到的固定形式数学模型为基础，而神经网络是通过对样本数据的直接训练建立模型的，前者灵活性略差，而后者的泛化能力更强，当进行合金热变形过程的预测时，神经网络能更好地适应新的变形条件，从而表现出有限元仿真难以实现的良好的细节预测能力，实现对微观组织分布状态更为细致的划分。综上，认为建立的BP神经网络模型可用于TA15合金多向锻造变形的微观组织预测。

4 结 论

1)热压缩实验结果表明：与双相区变形相比，单相区温度区间内的流动应力数值较低，且变形温度的改变对合金流动应力的影响较小，应力软化行为也并不明显。基于热压缩实验分别建立了TA15合金双相区和单相区温度区间内的热变形本构方程及动态再结晶模型。

2)基于Deform二次开发功能进行相关数学模型的程序化，实现了TA15合金多向锻造变形的微观组织仿真。仿真结果表明：在两个温度区间内，单道次压下率及变形温度均属于低道次下坯料平均晶粒尺寸的主要影响因子，随着变形道次累加，应变速率将对平均晶粒尺寸变化起主要影响，但整体上各因子影响力均呈下降趋势；在高温单相区各项因子取值变化对坯料平均晶粒尺寸的影响程度较之双相区有大幅缩减；模具结构主要影响晶粒尺寸的分布，使用闭式模具效果较好；多向锻造对于TA15合金晶粒尺寸的细化存在一定限度，随着道次累加，细化幅度降低。在实验条件范围内，提出了双相区及单相区温度区间内的多向锻造最佳因子组合。

3)参考各项因子在有限元仿真中体现的影响对象及强弱差异，建立了TA15合金多向锻造变形微观组织预报的BP神经网络预测模型，将预测结果与有限元仿真结果进行比较，结果表明两种方法的预测结果基本一致，但神经网络具备有限元仿真难以实现的良好的细节预测能力，能实现对微观组织分布状态更为细致的划分。