基于云模型和改进D-S证据理论的目标识别决策方法

尹东亮，黄晓颖, *，吴艳杰，何有宸，谢经伟

1.海军工程大学 作战运筹与规划系，武汉 430033 2.中国人民解放军91951部队，烟台 265100 3.海军工程大学 职业教育中心，武汉 430033

在军事领域中远程、超视距精确打击手段普遍应用。对于来袭目标，如导弹、无人机等的准确快速识别决策对战场态势变化极为关键。单一探测器已无法满足目标识别决策需求，通常是在目标识别决策系统中多探测器合作识别，存在多源信息与数据，需采取一系列信息数据融合方法[1-3]进行处理以提高数据的可靠性。然而由于战场环境中探测器可能受电子干扰等影响，所得信息中存在一定的难以判断的模糊信息[4]。云模型理论[5]于20世纪90年代被提出，用于解决定性问题量化的不确定性和信息数据的模糊性。

文献[6]基于信息融合和信息测度，利用云模型方法处理了不确定信息，对多准则群决策方法进行了改进；文献[7]结合改进粗糙集和云模型理论,提高了敌我空战模糊信息的处理能力，可以合理评估己方战机态势；文献[8]基于云模型针对风险评估中人为因素的模糊性和随机性建立了保护分析的云层，使得风险评估更为准确；文献[9]利用正态云模型考虑了评估专家判断的不确定性，提出正态灰云装备维修保障效能评估模型。

上述研究说明云模型能解决信息数据的模糊性，并可以对各类数据进行了转换描述。然而由于来袭目标的动态、智能变化，各探测器的侧重点及探测水平不同，探测器各探测周期所得信息难以统一，前期和后期数据难免存在偏差，甚至存在较大冲突互斥。D-S证据理论[10-11]作为解决数据差异及不确定性问题的工具，被广泛应用于数据融合[12]、目标识别[13]、决策评估[14]等领域。文献[15-17]通过利用各种系数或距离对证据理论中证据间冲突进行弥补；文献[18-20]通过改进证据融合算法对证据体融合的不足进行优化。这些方法针对性较强，普适性不足，难以对数据冲突和高度互斥的情况进行精确描述，可能得出与常理相悖的结论。

因此，本文提出基于云模型和改进D-S证据理论的目标识别决策方法。针对多探测器多源信息数据融合这一问题，将云模型引入解决定性问题量化的不确定性和信息数据的模糊性，利用改进后的D-S证据理论对多源信息融合中的数据冲突和高度互斥这一情况进行优化，提出冲突度、差异度、离散度3类衡量冲突大小的参数。最后，定义一种新的证据冲突参数对D-S算法进行证据修正，对目标识别结果进行决策，可为目标识别数据融合提供一种优化后的新思路、新手段。

1 基于云模型的目标识别准确性转化

中国工程院院士李德毅于1995年在概率论和模糊数学基础上提出了一种可以将定性语言值转化为数值进行量化描述的不确定性转换模型，称为云模型，可同时研究模糊性和随机性以及两者之间的关系。在云模型的实际研究中，已经证明自然科学和社会学领域中，大量不确定性问题的隶属云期望近似于正态云，尤其是一维正态云，下面对云模型相关概念进行介绍。

云模型有3个数字特征：期望Ex、熵En和超熵He。期望是指云滴在论域空间分布的期望值，是最能代表定性概念的点；熵En代表着定性概念不确定性的度量，可以用来描述云的跨度，反映了云滴的离散程度；超熵He是熵En不确定性的度量，代表熵的离散程度。

根据上述云模型定义，对各探测器各探测周期的目标识别准确性进行转化，具体步骤如下。

步骤1划分不同评价区间。

目标识别准确性是指根据某探测器某个探测周期所得目标信息判断出是否为某一目标的可能性。其语言描述具有一定的模糊性，设置包含5个语言值评语的评语集为{π1,π2,π3,π4,π5}={非常可能,较为可能,一般可能,不太可能,极不可能}。

对于目标识别的准确性，设定为以区间[0,1]的概率形式表示。因此将该评语集5个语言值评语划分为5个概率区间，分别确定为[0,a]、[a，b]、[b,c]、[c,d]、[d,1]，如图1所示。

图1 评语集概率区间

步骤2确定云模型数字特征。

对于区间[a-,a+]而言，决策者给出的属性值具有一定的稳定性，一般趋于一点，故区间值往往服从更贴近实际的正态分布。

正态分布ξ～N(μ,σ2)具备3σ原则，绝大多数随机变量落在区间(μ-3σ,μ+3σ)中，故令μ-3σ=a-，μ+3σ=a+，可得

(1)

表1 评价区间标准云数字特征

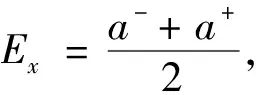
对于熵En，主要表示区间的不确定度。但由于区间边界值为模糊过渡值，分属于两区间，故取两相邻区间的期望值Ex表示熵En，计算公式为

(2)

超熵He表示熵的离散程度。由于决策者给出的属性值具有一定的稳定性，故其离散程度基本一致，此处一般依据经验而得，取He=0.01。

为更直观表示各朵标准云之间的区别，特取a=0.2、b=0.4、c=0.6、d=0.8。以此为例生成云图，如图2所示。

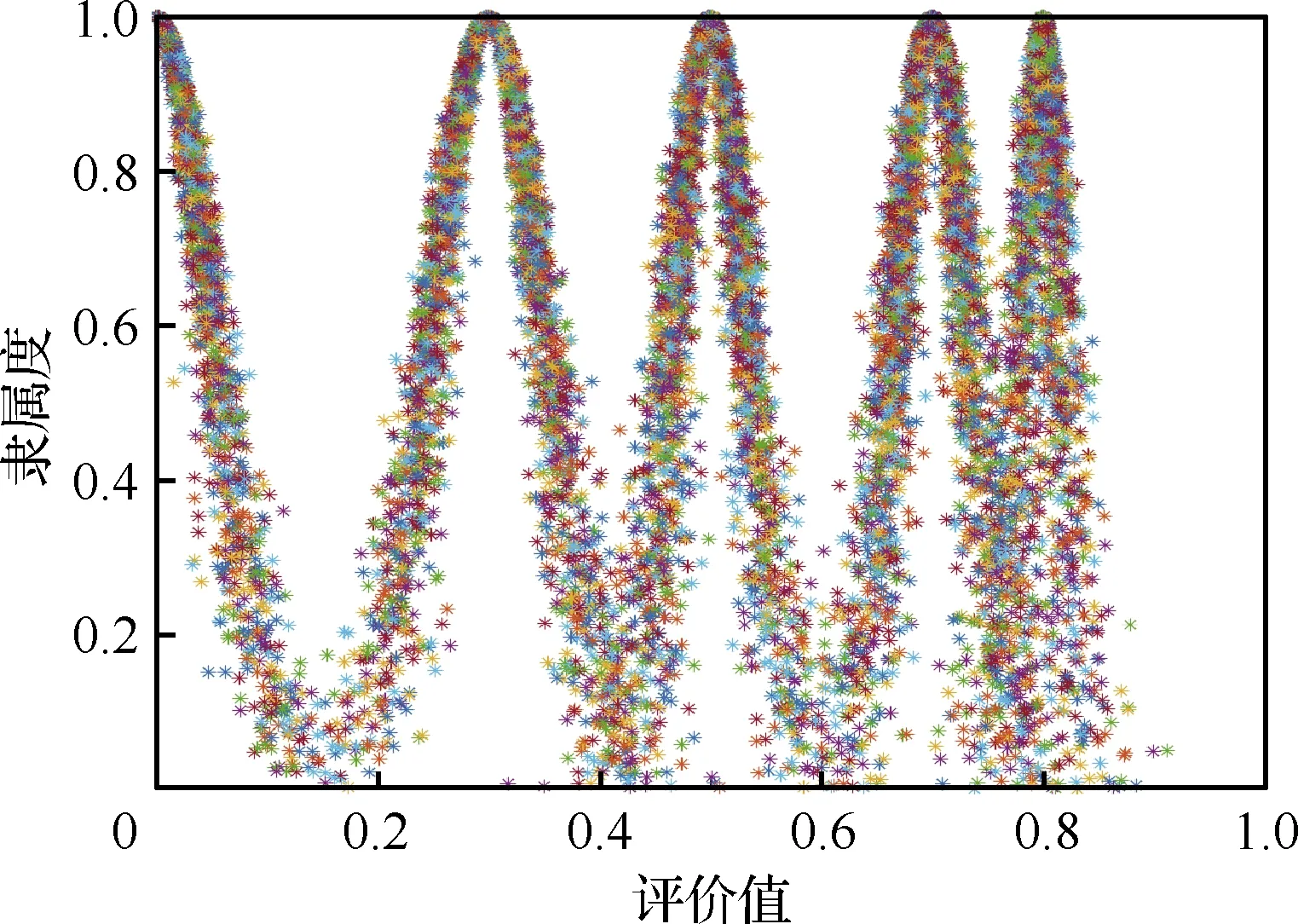
图2 目标识别准确性的标准云

步骤3构建隶属度矩阵。

(3)

根据计算所得隶属度构建第i个探测器的隶属度矩阵μi

(4)

2 基于改进D-S证据理论的目标信息融合优化算法

在探测器探测到某目标的初始探测周期，据探测信息识别目标并不一定准确。随着探测器持续探测，由于目标的动态变化，各周期所得探测信息也难以统一，甚至存在悖论、互斥，对目标识别决策造成了一定的难度。例如敌方某型反舰导弹攻击某驱逐舰，该导弹爬升、平飞、俯冲等各阶段的速度、高度、敌我夹角都不相同，因此根据驱逐舰单独某个探测周期所得信息识别目标难度较大，必须多周期信息融合综合识别，而由于来袭导弹攻击阶段不同，各周期信息也存在一定差异，需要对各周期信息差异、冲突进行融合优化。

D-S证据理论在多源信息融合处理方面具有一定的优势，对证据间的差异、冲突进行融合优化处理后，改进D-S证据理论，可有效解决多源信息的不确定性和信息融合冲突问题。首先对D-S证据理论的相关术语进行介绍如下：

定义2[10]令Θ表示一个由N个确定对象所组成的有限集合，称为识别框架Θ，Θ={1,2,…,N}，其中{1,2,…,N}仅代表元素，无实际意义，事件A包含于Θ。同时令P(Θ)表示Θ的幂集，包含2N个元素，每个元素代表事件A中的一个事件，即P(Θ)为事件A所有可能的子集合。

P(Θ)={∅,1,…,N,(1,2),(1,3),…,

(N-1,N),(1,2,3),…,Θ}

(5)

式中：∅为空集；称仅含单一元素1,2,…,N的为单点(Singleton)。则可定义从P(Θ)到[0,1]的映射，即基本概率分配函数(BPA，mass函数)为

m:P(Θ)→[0,1]

A→m(A)

根据定义2将第i个探测器的隶属度矩阵μi中各元素μijk转化为mass函数mi(Ak)j，表示第i个探测器第j个探测周期所得目标信息识别是否为目标Ak的基本概率分配函数。计算公式为

(6)

BPA矩阵为mi=[mi(A)j]=[mi(Ak)j]，mi(A)j=[mi(A1)jmi(A2)j…mi(Ak)j…mi(Am)j]表示第i个探测器Xi第j个探测周期对各目标的mass函数矩阵。

结合D-S证据理论，根据证据冲突融合的基本步骤可将证据冲突分为2类。一类是证据体自身之间的冲突，第1类冲突修正后，对各证据体进行融合，引发第2类冲突，即证据融合规则的不完善所造成的算法缺陷。下面对第1类冲突进行改进优化。

2.1 证据冲突计算

针对第1类证据冲突，目前有一定的研究，主要采用一系列冲突衡量指标，比如冲突系数、Jousselme距离、Pignistic概率距离、兰氏距离、聚焦度等，分别是对证据体自身间冲突不同角度的不同描述，均具有各自的局限性。其中冲突系数表示证据间冲突性，各种距离参数表示证据间相似性，两者无相关性[21]；而相较于前两者对证据之间的差异进行描述，聚焦度主要体现证据体自身的不确定性。

为了更全面地描述证据体第1类冲突，选取其中较具有代表性的多个指标综合考虑，改进D-S证据理论，根据冲突衡量指标的不同含义，将其分为3类，分别为冲突度α、差异度β、离散度γ。

2.1.1 冲突度α

冲突度α采用冲突系数K来表示，冲突系数K体现的是证据体之间的整体冲突，其定义为在同一个识别框架Θ下，事件A的mass函数可由2个证据体的mass函数合成，规则如下：

(7)

(8)

式中：B、C为事件A的子事件。

针对探测器不同探测周期目标信息所构成的证据体，令Kjj*(Xi)表示第i个探测器Xi第j个和第j*个探测周期证据体冲突系数，则冲突度αjj*(Xi)为

(9)

2.1.2 差异度β

差异度β采用Jousselme距离、Pignistic概率距离表示。Jousselme距离、Pignistic概率距离体现的是证据体之间在空间向量中距离的大小，描述证据间相似性。首先对这2个距离指标进行求解，其次根据其相同的特性和单调变化趋势，建立二维坐标系将其投影成向量，以坐标点到原点的距离表示差异度β。具体步骤如下。

步骤1计算Jousselme距离。

Jousselme等[22]于2001年提出Jousselme距离djj*(Xi|Ak)Jousselme，用以度量两证据间的相似情况。距离越大，证据相似度越小。定义距离djj*(Xi|Ak)Jousselme为

(A,B)→d(A,B)

(10)

式中：A、B为ϑ中的事件，具有以下特性(距离度量三公理)：非负性d(A,B)≥0；非退化性d(A,B)=0⟺A=B；对称性d(A,B)=d(B,A)；三角不等式d(A,B)≤d(A,C)+d(C,B)。

djj*(Xi)Jousselme=

(11)

步骤2计算Pignistic概率距离。

Liu[23]于2006年引入Pignistic概率函数，提出了Pignistic概率距离，对D-S证据理论进行了改进。Pignistic概率函数的关键是将证据体焦元层面的冲突通过博弈概率转换为信度层面的冲突，互斥的焦元间互不影响。这对于2条证据中彼此不存在有交集的焦元，只需要考虑证据之间每个命题的概率差即可，用最大差值表示证据间冲突程度。

Pignistic概率距离定义如下：令m表示识别框架Θ中的mass函数，则可定义从Θ到[0,1]的映射关联函数，即Pignistic概率函数BetPm(ω)为

(12)

式中：|A|为子集A的基数。

事件A的两证据体m1和m2之间的Pignistic概率距离定义为djj*(Xi|Ak)Pignistic，令djj*(Xi)Pignistic表示第i个探测器Xi第j个和第j*个探测周期证据mij和mij*之间的Pignistic距离，则

djj*(Xi)Pignistic=maxXi{|BetPj-BetPj*|}

(13)

步骤3计算差异度。

Jousselme距离、Pignistic概率距离均具有相同趋势的单调性，距离越大，则证据相似度越小。虽然Pignistic概率距离对Jousselme距离进行了改进和缺陷弥补，但这种博弈概率不满足距离度量三公理，故引入差异度将两者进行向量融合，使其互相弥补，又满足距离度量特性，引入向量的概念，建立二维坐标系，将Jousselme距离、Pignistic概率距离表示为坐标点，即(x,y)⟺(djj*(Xi)Jousselme,djj*(Xi)Pignistic)。则定义该坐标点到原点的距离为差异度βjj*(Xi)，计算公式为

βjj*(Xi)=

(14)

2.1.3 离散度γ

离散度γ采用聚焦度θ来表示。聚焦度θ表示单个证据体自身的不确定性，θ越大，不确定性越小。

令θj(Xi)是第i个探测器Xi第j个探测周期的证据mij的聚焦度，可表示为

0≤θj(Xi)≤1

(15)

为了保持冲突度α、差异度β、离散度γ三者单调性一致，便于下一步改进，需对聚焦度进行转化。

令γj(Xi)表示第i个探测器Xi第j个探测周期的证据mij的离散度，定义γjj*(Xi)=1-|θj(Xi)-θj*(Xi)|，则聚焦度越小，离散度就越大，同时证据体自身不确定性越大。

2.2 证据冲突修正

根据2.1节所得冲突度α、差异度β、离散度γ的计算方法，这3类冲突指标融合了前人提出的多种冲突系数，基本涵盖了证据体第1类冲突的各类情况。同时可以得出其共同特点和性质：这3类冲突指标在定义上具有数学上向量和距离的含义，衡量参数值越大证据冲突越小，具有相同的单调变化趋势。

故根据冲突度α、差异度β、离散度γ的向量和距离的含义引入立体空间的相关性质进行D-S证据理论的改进优化，将冲突度α、差异度β、离散度γ分别投射到三维坐标系的x轴、y轴、z轴上，即(x,y,z)⟺(αjj*(Xi),βjj*(Xi),γjj*(Xi))，如图3所示。

图3 改进后新的证据冲突参数三维空间向量

将点(αjj*(Xi),βjj*(Xi),γjj*(Xi))到原点(0,0,0)的距离定义为一种新的证据冲突参数δjj*(Xi)，表示第i个探测器Xi第j个和第j*个探测周期改进后的一种新的证据冲突参数，计算公式为

(16)

(17)

将证据差异转化为证据可信度，令νj(Xi)=1-φj(Xi)，从而引出可信度矩阵v(Xi)为

(18)

将各探测周期总可信度vj(Xi)与最大总可信度相比，即可得出第i个探测器Xi第j个探测周期证据修正系数σj(Xi)为

(19)

式中：0≤σj(Xi)≤1。

最后结合证据修正系数σj(Xi)对证据进行修正：

(20)

2.3 证据融合优化

对第1类证据冲突进行修正后，下面对第2类证据冲突，即证据融合规则算法进行分析改进。证据修正系数只解决了BPA的权重比例，消除了证据体之间的差异化，但并未解决证据体之间的全局焦元分配，使得全局焦元分配具有一定的主观性。

(21)

式中：f(Ak)为第k个目标Ak证据体的焦元值局部冲突分配函数。

2.4 目标识别决策

通常，决策判断最大mass函数所对应的目标为目标识别系统发现的目标。但当各目标mass函数之间差距较小或存在两相同最大值时判断不准确，故对目标识别决策判断条件进一步细化。

步骤1判断m*(Φ)≤ε1，若满足则所取探测周期数已可满足目标识别决策条件，证据体充足。若m*(Φ)>ε1，则说明证据体不足，需继续探测获取更多目标信息重新开展目标识别决策，一般取ε1=0.05。

目标识别综合决策具体流程如图4所示。

图4 目标识别综合决策流程

3 算 例

3.1 算法正确性验证

以某型目标识别决策系统为例，选取4个探测器{X1,X2,X3,X4}，令各探测器权重ω=[0.15, 0.40,0.35,0.10]，每个探测器选取4个相同时间的探测周期{1,2,3,4}，探测到目标后预判目标集为{A1,A2,A3,A4,Ax}，其中Ax表示目标库中未预判匹配到的未知目标，取a=0.2、b=0.4、c=0.6、d=0.8。

根据目标识别决策系统中各探测器各周期的目标信息对预判目标集中各目标识别准确度进行判断，限于篇幅，仅对探测器X1进行展示，其各周期对各目标识别准确度评语如表2所示。将表2评语转化为云决策矩阵如表3所示。

表2 探测器X1各周期对各目标识别准确度评语

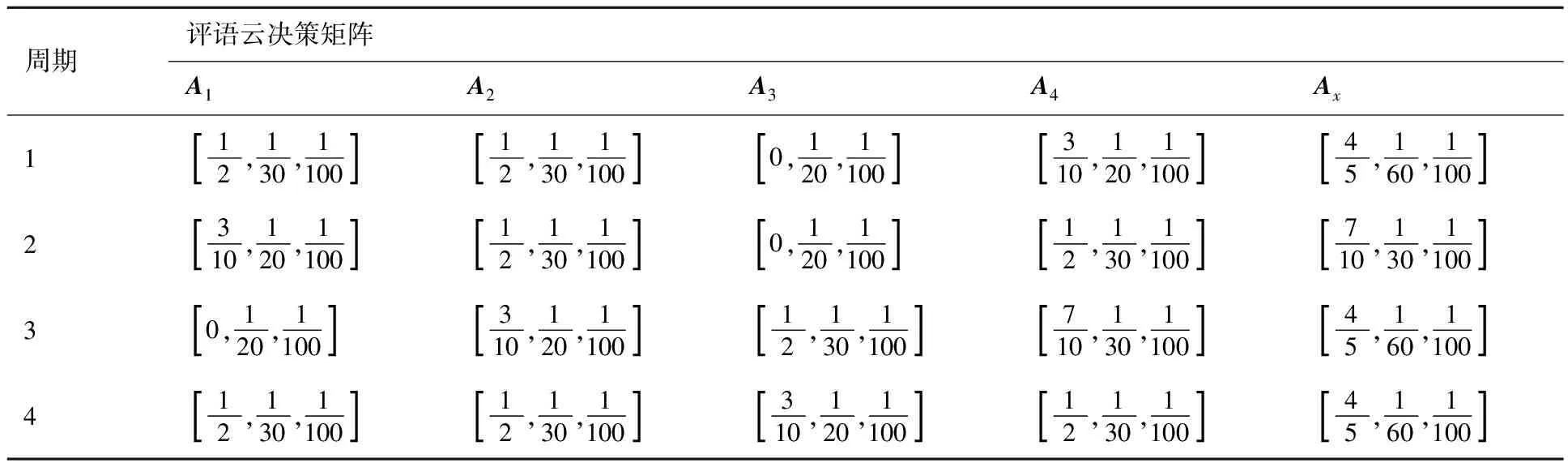
表3 探测器X1各周期评语云决策矩阵

由式(3)计算隶属度，进而根据式(6)计算探测器X1的mass函数，构建mass函数矩阵m1

根据mass函数矩阵m1由式(7)～式(15)分别计算4个探测周期证据体之间的冲突度α、差异度β、离散度γ，如表4所示。

表4 探测器X1各周期证据冲突衡量指标

由式(16)～式(19)计算得出探测器X1各周期证据修正系数，分别为σ1(X1)=0.991 9，σ2(X1)=1.000 0，σ3(X1)=0.988 4，σ4(X1)=0.994 2。

对目标决策结论进行分析，目标识别综合决策的mass函数m(A)中各元素值大小区分明显清晰，不存在各元素值大小相近的情况，决策效果较好，结论清楚统一，证明了本文改进后算法的正确性和高效性，稳定性较高。

3.2 算法识别效果对比分析

为了验证本文提出的基于云模型和改进D-S理论的目标识别决策方法的高效性和有效性，本文在使用本文提出的融合方法计算得到融合结果后，继续以3.1节算例输入数据进行结果分析，利用D-S理论的Dempster合成规则[24]这一经典融合方法以及以往改进的多种数据融合算法[25-28]分别计算相应的结果，与本文方法进行分析对比，限于篇幅，仅对各方法所得探测器X1融合结果以及最终的目标识别决策结论进行体现，如表5所示。

对表5数据进行分析，将6种不同方法进行对比，如图5～图6所示。

表5 不同数据融合方法所得结果

图5 不同方法探测器X1的mass函数对比

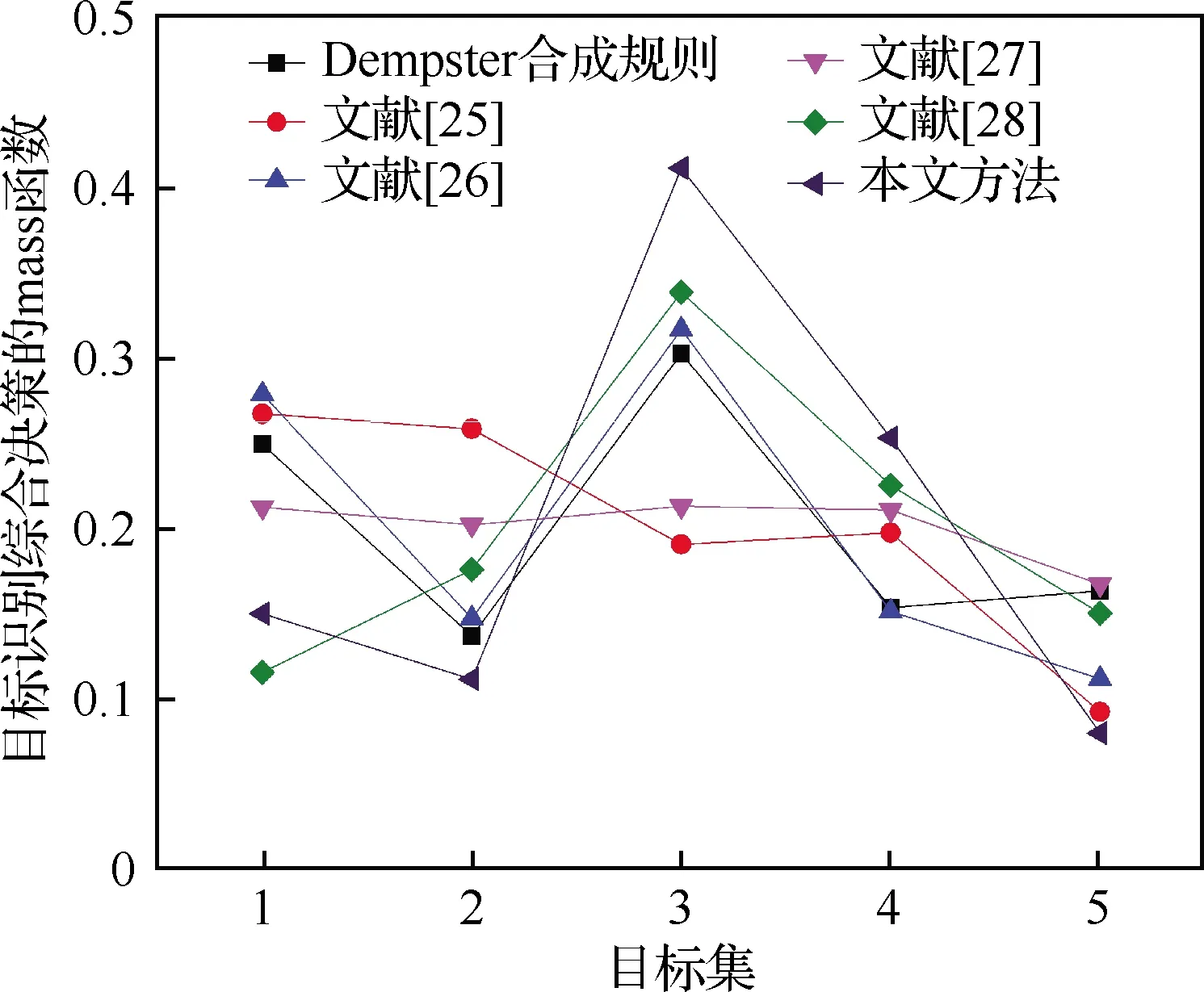
图6 不同方法目标识别综合决策的mass函数对比

由表5、图5、图6可以看出，文献[25]、文献[27]的方法所得mass函数差距不明显，基本接近，难以对目标进行有效的识别决策。而Dempster合成规则和文献[26]所得目标1、3的mass函数接近，虽然能识别出目标，正常开展目标决策，但其对目标2、4、5识别的mass函数值较为接近，尤其目标5是目标库中未预判匹配到的未知目标，这样没有有效对各目标进行区分，后续识别决策往往需要增加更多的探测周期以确保识别准确。文献[28]能有效识别目标且各目标识别mass函数差距较大，但其对未知目标5的识别mass函数较大，容易出现识别错误的情况。本文方法对各目标识别的mass函数之间的差距明显较大，且目标5识别mass函数较小，对全局目标识别影响较小，具有一定的优越性，识别效果最佳。

3.3 算法收敛性对比分析

通过3.2节对算法目标识别效果的分析，可以看出，部分文献算法需较多周期的探测数据才可能对目标进行准确识别，下面对各算法的收敛性进行对比分析，演示各算法达到性能稳定时所需的探测周期数，如图7所示。

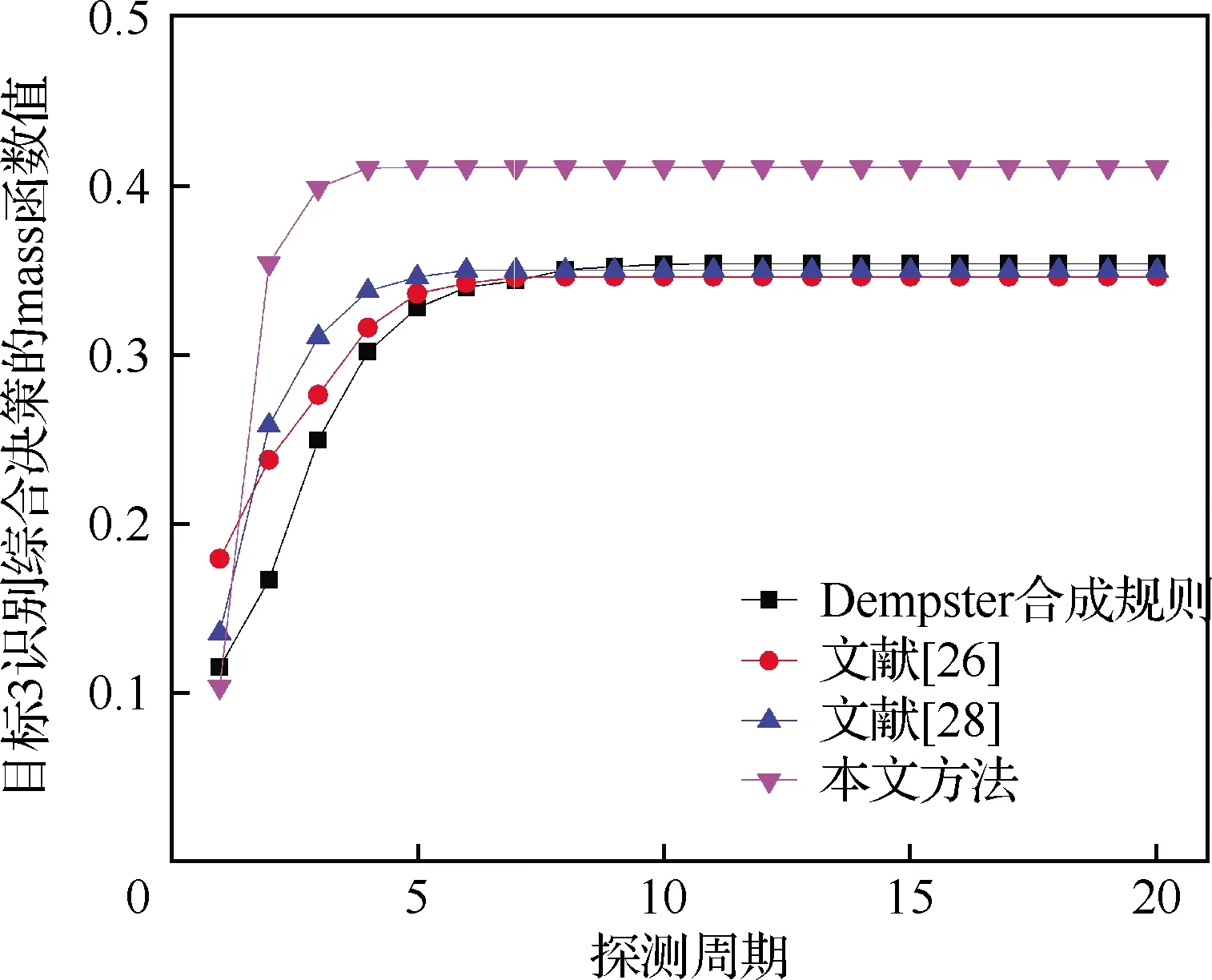
图7 不同方法下目标3识别综合决策的mass函数对比

对图7结果进行分析，可以看出，本文算法仅需要较少周期(4个周期)的融合即可以达到性能稳定，算法收敛速度高于其他融合方法，验证了本文算法良好的收敛性和稳定性。

4 结 论

针对目标识别决策系统中多探测器多源信息融合的模糊性和信息冲突互斥的问题，本文基于云模型和D-S证据理论，研究改进出了一种新的证据冲突修正和融合优化算法。通过引入冲突度、差异度、离散度3类衡量冲突大小的参数，定义了一种新的证据冲突参数，同时考虑证据焦元分配改进了证据冲突融合算法，结合各探测器权重加权得出各目标综合识别决策的mass函数，基于最大隶属度原则对目标进行决策。最后结合算例，验证该方法的适用性，为目标识别决策提供了一种改进的解决方法，具有一定的实践价值。