基于GPI的三自由度直升机系统姿态控制研究

王玲玲，毋飞龙

(1.海军航空大学 岸防兵学院，山东 烟台 264000; 2.海军91213部队， 山东 烟台 264000)

1 引言

直升机是一种利用旋翼提供升力和推进力的飞行器，与固定翼飞机相比，它可以实现低空、低速飞行，并能垂直起降和空中悬停，因此直升机在军用和民用方面有了很大的发挥空间[1]。而且由于直升机是一种多输入多输出的非常复杂的被控对象，其对控制理论的研究和应用有着重要的工程意义，因此直升机也同样成为控制理论研究中的一种广泛研究对象。本文所研究的对象是三自由度直升机实验平台，它是一种由2个水平旋翼提供升力，与另一侧的平衡块构成的一种飞行器实验装置，可以围绕立柱模拟飞行器俯仰、偏转姿态，同时通过2个水平旋翼提供的升力差模拟飞行器的倾斜姿态，如图1所示。

图1 三自由度直升机系统示意图Fig1.Diagram of 3-DOF helicopter system

目前，对该对象的研究多用来解决对飞行姿态的控制，采用的算法多为PID控制算法，如文献[2-3]；或是对PID算法的改进[4]，如模糊PID[5-8]、神经网络PID等[9-10]。理想条件下PID的相关控制算法已经能够达到较好的控制效果。而当参数变化时或者受到外界不确定性干扰时，为了保证较好的控制效果，国内外研究学者也做了若干研究，如U.Pérez-Ventura[11]研究的当执行机构的电压变化时，采用连续螺旋算法确保控制的鲁棒性；YANG Qiwei[12]则是通过对系统控制输入输出解耦，对各自解耦的部分采用非奇异终端滑模控制来保证鲁棒性；Hicham Chaoui[13]则是针对结构性和非结构性不确定性分别设计自适应控制和参考模型，来应对不确定性对系统的影响。本文研究在跟踪频率变化信号或者恶劣噪声环境下，如何改善传统PID算法中的微分项对控制效果带来的不利影响。本文以积分重构的思想，用控制量的积分代替被控量的误差微分估计，即采用广义比例积分控制算法(GPI)来实现飞行器的角度控制[14-15]，对姿态控制抗外界干扰的研究具有一定的参考价值。

2 数学模型

对图1系统中的俯仰轴、横侧轴、旋转轴分别进行力矩分析，忽略重力矩和干扰力矩，建立三轴模型为：

(1)

式(1)中：ε、p分别为俯仰轴、横侧轴角度；γ为旋转轴角速度；Je、Jp、Jt分别为俯仰轴、横侧轴、旋转轴转动惯量；Kc为螺旋桨电机的升力常数；l1为螺旋桨到俯仰轴支点的距离；lp为螺旋桨到横侧轴支点的距离；Us为2个电机电压之和；Ud为2个电机电压之差；G3为2个螺旋桨的等效重力。参数建模示意如图2所示。

图2 参数建模示意图Fig.2 Diagram of modeling

由式(1)可知，俯仰轴、横侧轴、旋转轴的被控对象传递函数依次为：

(2)

(3)

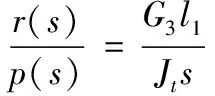
(4)

式(2)～(4)中，各常变量参数的含义及取值如表1所示。

表1 三自由度直升机系统参数

3 基于GPI的飞行器姿态控制

设计GPI控制器来完成姿态控制，指标要求如表2所示。

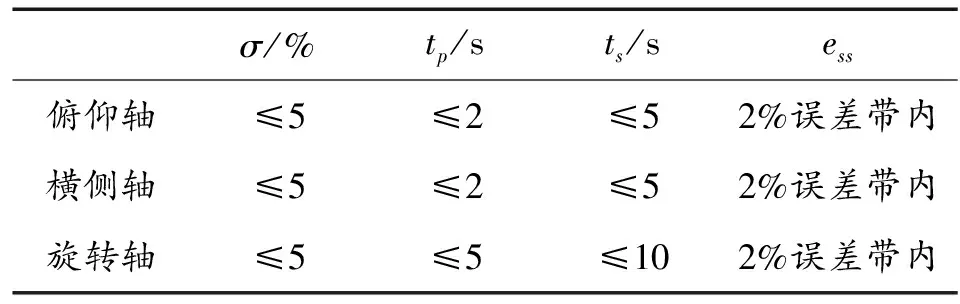
表2 各通道姿态控制的指标要求

3.1 俯仰通道GPI算法设计

由前文俯仰通道的模型可知，俯仰角ε与控制输入电压Us之间的关系式为：

(5)

式(5)中，d为常值干扰信号。

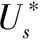
(6)

由式(5)～式(6)可得：

(7)

(8)

(9)

将式(9)代入式(8)有：

(10)

仍然延续PID控制律的设计思路，此时，可以令控制输入的误差eUs为[14-17]：

(11)

即控制输入仍然是通过被控量误差的比例积分微分控制。

将式(11)代入式(7)，此时可以求出控制律下的特征多项式方程，即：

(12)

(13)

(14)

易得复数域下的特征方程为：

s4+λ3s3+λ2s2+λ1s+λ0=0

(15)

继续对式(9)求导，得：

(16)

(17)

同时对式(12)求二阶导，并将式(16)和式(17)代入后有：

(18)

对式(18)进行拉氏变换，得：

(19)

由此便得到控制输入和俯仰角偏差之间的传递关系为：

(20)

3.2 横侧通道的GPI算法设计

由前文横侧通道的模型可知，简化后的横侧角p与控制输入电压Ud之间的关系式，和俯仰角ε与控制输入电压Us的关系式类似，都是二阶关系，因此，与上述过程同理设计可得横侧通道的GPI控制律，有：

(21)

以及GPI控制下的特征方程为：

s4+β3s3+β2s2+β1s+β0=0

(22)

同理，亦可得到控制输入eUd和横侧角偏差ep之间的传递关系为：

(23)

3.3 旋转通道的GPI算法设计

(24)

(25)

由式(24)～式(25)可得：

(26)

对式(26)积分可得：

(27)

令

(28)

此时，设计GPI控制律，有：

(29)

将式(29)代入式(26)，有：

(30)

对式(30)求二次导，有：

(31)

对式(26)和式(28)分别求导，可得：

(32)

将式(32)代入式(30)可得：

(33)

对式(33)进行拉普拉斯变换，得：

(1+τ3)s3+τ2s2+τ1s+τ0=0

(34)

则式(34)就是旋转通道GPI控制下的特征方程，通过配置τi(i=0，1，2，3)使系统稳定且达到指标要求。

继续对式(28)求导，有：

(35)

对式(29)求二阶导，并将式(35)代入后，有：

(36)

对式(36)进行拉氏变换得：

(37)

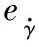
(38)

3.4 参数设计

根据指标要求可以绘制出3个通道期望的闭环零极点范围。由于俯仰通道和横侧通道的期望一致，因此可以绘制这2个通道的闭环零极点范围，如图3所示。同时根据主导极点的概念，可以设置一对远离虚轴的负实极点，对旋转通道来说，由于是三阶系统，可以设置一个远离虚轴的负实极点，则3个通道的系统响应完全可以由各自的一对复数极点来决定。

图3 极点配置示意图Fig.3 Diagram of poles distribution

由此，式(15)、式(22)所表征的四阶系统，式(34)所表征的三阶系统，都降阶为二阶系统进行讨论。

对于俯仰通道来说，假设复数极点为s1，2，负实数极点为s3，4，则有：

(s-s1)(s-s2)(s-s3)(s-s4)=

s4+λ3s3+λ2s2+λ1s+λ0=0

由此可确定控制律参数λi(i=1，2，…，4)，同理可确定横侧通道控制律参数βi(i=1，2，…，4)以及旋转通道控制律参数τi(i=0，1，2，3)。

3.5 仿真分析

3.5.1俯仰通道仿真分析

根据式(20)可以得到俯仰通道GPI控制系统结构图，如图4。

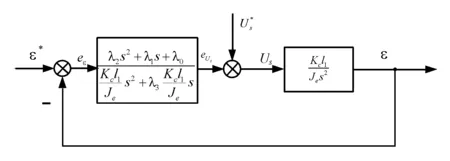
图4 俯仰通道结构图Fig.4 Block diagram of pitching channel

而λi已由极点配置决定，接下来就是调整λi去满足指标要求。

在阶跃输入下，根据极点配置，调整一组GPI控制参数至最佳响应，当λ0=153，λ1=730.2，λ2=948.17，λ3=60.8时，同时根据相近的极点配置，设置PID参数分别为Kp=4.154 2，Kd=5.293 7，Ki=0.876 6，得到PID的响应曲线如图5所示。

图5 相近极点配置下俯仰轴的阶跃响应曲线Fig.5 Step response of pitch axis with similar poles assignment

同样，在阶跃输入下，βi不变，在恰好满足指标需求的条件下，取一组PID参数，得到响应曲线如图6，此时PID参数分别为Ki=0.001，Kp=2，Kd=0.8。

图6 调整PID参数至最佳时俯仰轴的阶跃响应曲线Fig.6 Step response of pitch axis when PID parameters are adjusted to the best

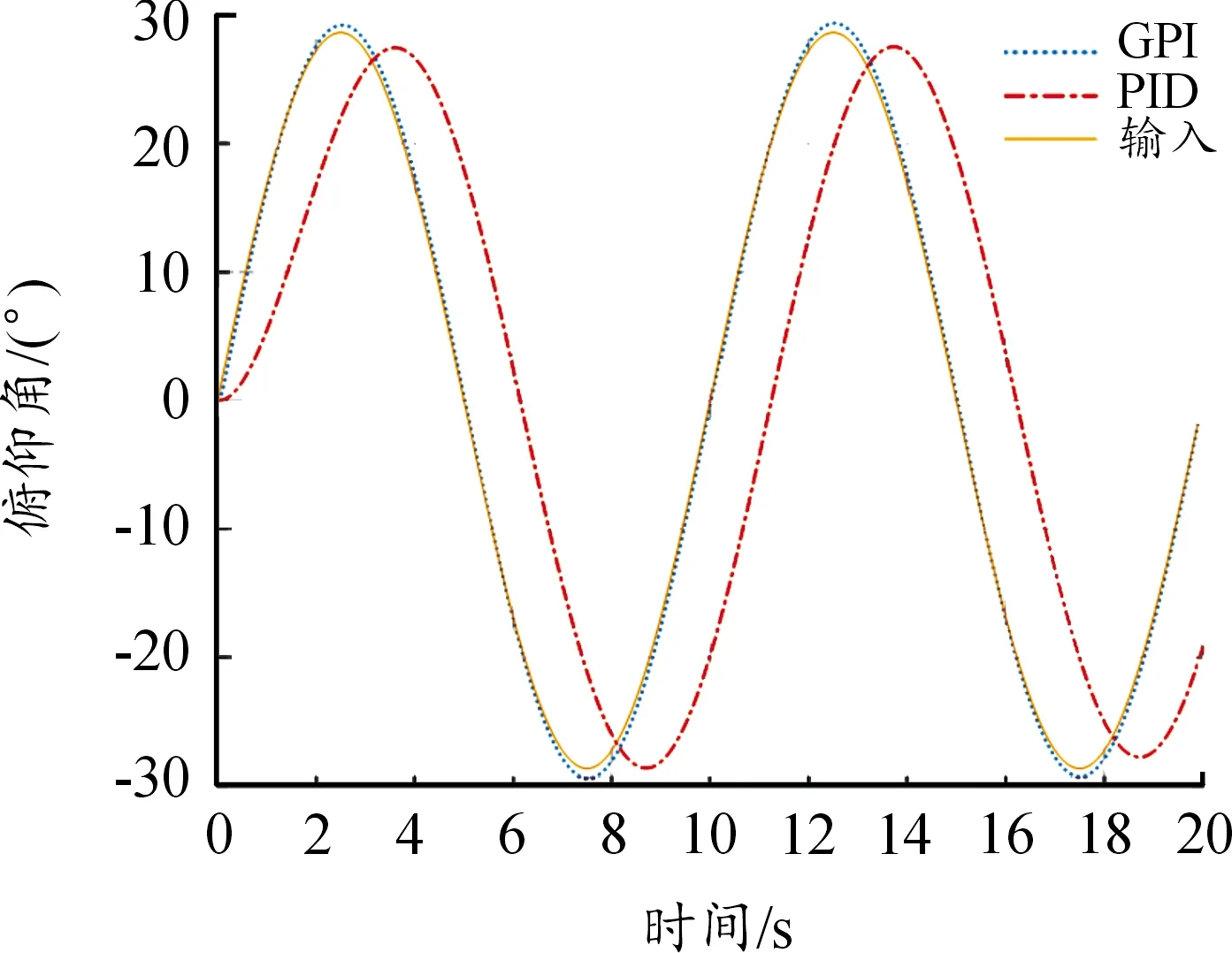
图7 相近极点配置下俯仰轴的正弦响应曲线Fig.7 Sine response of pitch axis with similar poles assignment

图8 调整PID参数至最佳时俯仰轴的正弦响应曲线Fig.8 Sine response of pitch axis when PID parameters are adjusted to the best

通过以上仿真曲线可以看出，PID在相近极点配置下，并没有满足性能指标要求，而在能够满足指标要求的参数搭配下，由于其提高了快速性，降低了超调量，而丧失了一定的对频率快速变化信号的跟踪能力，如果系统中一旦出现高频干扰，其跟踪性能将会进一步丧失，这一点从PID算法的抗干扰分析中也可以看出。而且我们从GPI和PID这2个控制器附加的开环零极点也能看出，GPI比PID多增加了一个位于左半平面远离虚轴的极点，相应地，其快速性指标要优于PID控制，跟踪不同信号下的适应性更好。

在横侧通道和旋转通道中，应用GPI和PID控制也有类似的结论，因此后续只讨论GPI作用下的姿态控制和角速度控制，不再对GPI控制与PID控制做分析比较。

3.5.2横侧通道仿真分析

根据式(23)可以得到横侧通道GPI控制系统结构图，如图9。

图9 横侧通道结构图Fig.9 Block diagram of transverse channel

图10 横侧轴的阶跃响应曲线Fig.10 Step response of transverse axis

图11 横侧轴的正弦响应曲线Fig.11 Sine response of transverse axis

3.5.3旋转通道仿真分析

根据式(38)可以得到旋转通道GPI控制系统结构图，如图12。

图12 旋转通道GPI控制结构图Fig.12 Block diagram of GPI control for roll channel

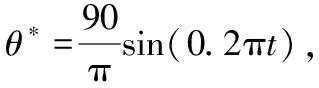
图13 旋转角速度的阶跃响应曲线Fig.13 Step response of rotational angular velocity

图14 旋转角速度的正弦响应曲线Fig.14 Sine response of rotational angular velocity

3.5.4横侧通道和旋转通道的串级GPI控制

由式(1)知，改变直升机横侧轴的倾斜角大小可以控制直升机的旋转速度。如此根据横侧轴及旋转轴之间的相关性，可以将其设计为串级控制，其中，旋转通道的横侧角输出作为横侧通道横侧角的期望值，横侧与旋转的串级控制如图15所示。

阶跃下的旋转角速度响应曲线如图16，阶跃下的横侧轴横侧角响应曲线如图17。

图16 串级控制旋转轴角速度响应曲线Fig.16 Angular velocity response of cascade control in roll channel

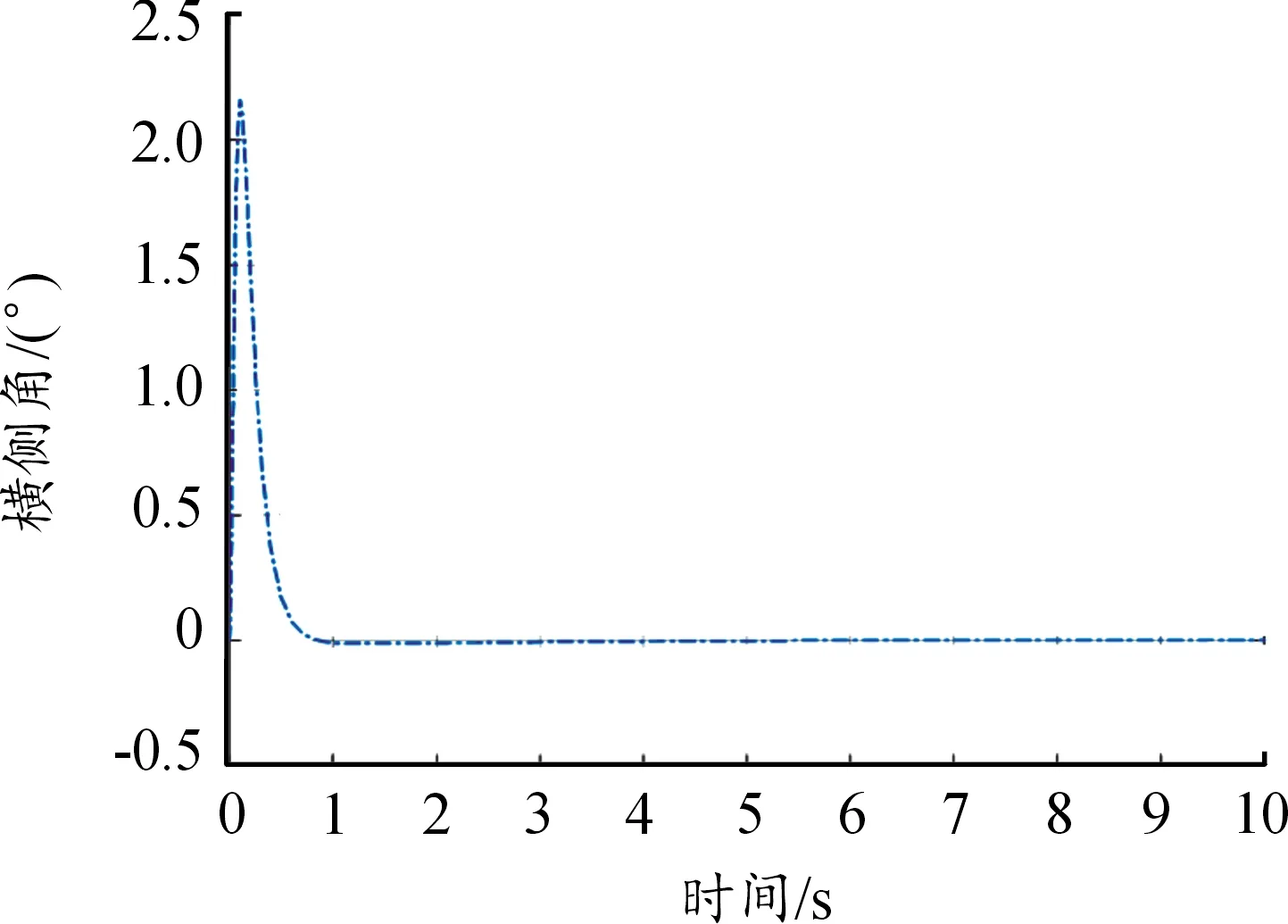
图17 串级控制下的横侧角响应曲线Fig.17 Transverse angle response with cascade control

通过以上3个通道的仿真实验，不难看出，在相同极点配置下，PID并没有满足性能指标要求。虽然其有自身的一套参数可以满足，但由于其提高了快速性，降低了超调量，而丧失了一定的对频率快速变化信号的跟踪能力，因此相对于PID来说，本文设计的GPI控制具有更好的跟踪适应性。

4 结论

本文以三自由度直升机为研究对象，在姿态控制中，当跟踪频率变换较快的信号或系统当中充满高频信号时，常规的PID算法中的微分项对此类信号较为敏感，造成算法的参数适应性较差，不易满足指标要求等问题，本文在积分重构思想基础上，以控制量的积分代替被控量的误差微分估计，并通过高阶求导，使被控量的误差微分估计等于其实际值，从而使控制算法可以实际可操作。如此设计的广义比例积分算法可以使被控对象在恶劣噪声环境下实现姿态控制，满足指标要求，且具有较高的适应性。