一种探空火箭的落点位置及倾角散布控制方法
2022-01-10黄思亮李世玲李映华
徐 林,黄思亮,李世玲,李映华
(中国工程物理研究院电子工程研究所,四川绵阳 621900)
0 引言
在某探空火箭试验任务中,为确保良好的外弹道测量及载荷试验条件,要求对弹头落点位置及弹道倾角散布进行有效控制并尽可能提升落地速度。同时,为适应快速发射、长期贮存以及低成本化的研制需求,该探空火箭采用了全固体动力、无推力终止系统以及简化的二子级姿控执行机构设计方案。在此条件下,如何设计可行的制导控制方案成为飞控系统需要解决的重要问题。
针对固体火箭的耗尽关机制导控制问题,姿态机动能量管理[1-2]、倾角迭代闭路制导[1,3-4]、零射程线制导[5-6]是目前主要的解决方法。文献[1]提出了在闭路制导前通过改变姿态角进行部分能量耗散,在闭路制导段通过调整速度倾角约束适应剩余随机多余能量的混合制导方法。文献[2]在文献[1]的基础上提出了能量耗散效率更高的姿态角变化模型,降低了导弹姿态角速度。文献[3]提出了利用加速度表测量结果对耗尽关机时间进行预估,并在常姿态导引段调整倾角进行关机时间偏差修正的方法。文献[4]对速度倾角的迭代计算方法进行了改进,通过在实时速度的基础上叠加合适的速度增加量,提升了迭代收敛速度并降低了控制系统姿态跟踪误差造成的落点偏差。文献[5]建立了考虑地球旋转的零射程线制导法计算模型,并通过导弹末修级标准程序设计、多头分导方案设计等算例验证了该制导方法的有效性。文献[6]设计了对关机时间变化不敏感的零射程线导引律和末速精调导引律,提高了耗尽关机制导方法的精度。这些方法对于落点精度的控制是有效的,但对姿控执行机构的要求较高,同时能量耗散、倾角调整有悖于提升落点速度以及控制弹道倾角散布的需求,无法应用于文中需要研究的探空火箭制导控制问题。文献[7-8]分别通过二级姿态角和点火时刻的自适应调整,减小了探空火箭弹道参数散布,但所采用的调整策略均属基于蒙特卡洛打靶统计结果的经验方法,难以实现高精度多约束控制目标。文献[9-10]将发动机持续助推对轨道参数的影响等效为脉冲瞬时矢量,推导出了一种基于定轴飞行的定点制导算法(PA),解决了多级固体运载火箭的入轨控制问题。该方法的本质是通过调整级间滑行时间、发动机定向推力方向来分别适应目标轨道位置及速度约束,但对发动机预示推力精度有较高要求,同时缺乏对点火后干扰因素(发动机推力偏斜、导航姿态角误差)的修正能力。文中将二级姿态角和点火时刻同时作为控制变量,设计了一种新的闭路制导与点火时刻自适应调整相结合的制导方法,为耗尽关机、姿控能力以及速度约束下的探空火箭落点倾角和位置散布控制问题提供了可行的解决途径。
1 制导方案
探空火箭为二级固体火箭,一级助推段在大气层内按预定程序和横法向导引飞行,二级在真空段飞行并完成助推加速,最终以惯性方式再入。由于一级助推段制导方法限制以及气动、气象、推力等干扰组合影响,一级飞行弹道将产生较大散布,如何修正或者适应这些偏差以实现按预定倾角飞抵预定落点便是二级制导需要解决的问题。
为便于后续制导方案阐述及算法推导,对问题简化处理如下:
1)将地球视为匀质圆球,暂不考虑地球形状及质量分布不均引起的引力摄动;
2)暂不考虑地球旋转引起的惯性力(离心惯性力、哥氏惯性力)对弹道的影响;
3)暂不考虑再入空气动力影响。
需要说明的是,地球引力摄动、自转引起的惯性力以及再入空气动力因素对弹道的影响并不可忽略。考虑到探空火箭射程、射向相对固定,再入弹道倾角和飞行时间散布不大,上述简化处理所造成的弹道偏差可近似认为是系统性误差,并通过引入虚拟目标对真实目标进行适当修正的方式予以补偿。
在上述假设下,探空火箭二级助推前后均沿绕地球的椭圆弹道飞行,如图1所示。为便于阐述,下文直接称二级助推前的惯性飞行椭圆弹道为一级椭圆弹道,称期望的二级助推后惯性飞行椭圆弹道为二级期望椭圆弹道。其中,一级椭圆弹道参数由火箭出大气层后的状态决定,二级期望椭圆弹道的参数可在给定虚拟目标点处的位置、速度后确定。因此,该探空火箭的二级制导问题可以视为两条已知椭圆弹道间的转移问题。如果通过二级制导飞行恰好能够从一级椭圆弹道转移到二级期望椭圆弹道,则理论上即可精确实现探空火箭的落点位置及倾角控制目标。

图1 探空火箭弹道示意图
根据图1,在二级耗尽关机、位置增量不可调节的前提下,为了实现从一级椭圆弹道到二级期望椭圆弹道的转移,二级点火的位置会受到限制,合理的二级点火位置需要根据一级弹道偏差情况具体确定。一种简单可行的方案是,当两条惯性飞行椭圆弹道相交或者二者的距离减小到一定程度时,给出二级发动机点火指令。此时,火箭位置已在期望的二级椭圆弹道附近,但飞行速度还远小于期望值。又由于二级期望椭圆弹道上各点的状态参数均是确定的,因此可采用经典的闭路制导方法进行二级助推过程中的导引,使火箭飞行速度沿待增速度方向快速增加,直至耗尽关机。
2 二级点火时刻的确定
如图2所示,M点为虚拟目标,火箭飞出大气层后在K点给出二级点火指令,K点与地心的连线同二级期望椭圆弹道相交于N点,a为二级期望椭圆弹道的远地点,ξM,ξN分别为M点和N点的真远点角。rM,rN,rK分别为M点、N点以及K点的地心距。根据制导方案,可以将N点与K点之间的距离作为二级自适应点火的判断条件。为此,首先需要获得rK,rN的数值。

图2 二级点火时刻确定示意图
K点地心距rK及M点地心距rM计算公式为:
(1)
(2)
其中,(R0x,R0y,R0z)为发射点地心矢径在发射坐标系下的分量;(XK,YK,ZK)为K点在发射坐标系下的坐标,通过组合导航系统获得;(XM,YM,ZM)为M点在发射坐标系下的坐标,在真实目标坐标基础上叠加系统性偏差修正量后获得。
利用K点、M点的位置坐标和地心距可以求出两点间的射程角:
(3)
给定M点的速度大小VM和速度倾角ΘM,则二级期望椭圆弹道参数可确定为:
(4)
(5)

M点处的真远点角为:
(6)
N点处的真远点角为:
ξN=ξM-βKM
(7)
利用真远点角ξN、半通径P、偏心率e,即可求出N点处的地心距:
(8)
假设不进行二级点火,探空火箭一级关机后的飞行高度将先随时间增加,到达顶点后再逐渐减小,因此在探空火箭出大气层后的无动力滑行飞行过程中,必然存在某个时刻满足rN=rK或者rN-rK取得极小值。于是二级点火条件可表示为:
rN-rK≤ε
(9)
式中参数ε代表满足点火条件的最小距离。对于极端偏差条件下一级椭圆弹道高度过低可能导致的式(9)始终无法满足的情况,则rN-rK取得极小值的时刻即为二级点火时刻。由于二级闭路制导不可能瞬时改变速度方向,若ε<0将会出现火箭高度超过期望弹道的情况。为尽可能使弹道转移过程平稳,ε应为一定大小的正数,具体数值依据二级视位置增量等参数确定,亦可适当减小期望弹道上虚拟目标点处的倾角约束值。
3 二级闭路制导
二级闭路制导的主要目标是通过调整发动机推力方向,使火箭飞行速度沿待增速度方向增加,最终使耗尽关机时的位置、速度大小和方向均接近期望的二级椭圆弹道。根据椭圆弹道理论,为具体确定经过两点的弹道参数,只需再给定其中一点的速度大小、速度方向或者两点间的飞行时间。考虑到探空火箭无推力终止能力,采用约束速度方向、飞行时间的方式将会遇到速度大小难以控制的问题。又由于制导飞行过程中火箭速度变化剧烈,按给定火箭实时位置、速度大小的方式进行制导会导致需要速度方向持续改变,不利于简化的姿态控制系统控制实现。因此,采用一种新的直接给定虚拟目标点速度大小的方式进行闭路制导。考虑到不同干扰条件下的火箭飞行速度必然存在差异,为保证关机点附近制导指令始终平稳,虚拟目标点处的速度大小参照最大可能速度进行设置。
设二级闭路制导虚拟目标点M处的速度大小为VM,地心距为rM,火箭实时位置K点处的地心距为rK,根据能量守恒原理,可得火箭实时位置处的需要速度大小为:
(10)
根据椭圆弹道理论,K点处需要速度倾角θKr满足:
2rMtan2(βKM/2)tan2θKr+2vKrKtan(βKM/2)tanθKr+
tan2(βKM/2)(2rM-vK(rK+rM))+vK(rM-rK)=0
(11)
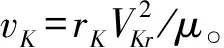
(12)
该结果中的两个倾角数值分别代表了高、低弹道。考虑到探空火箭二级飞行射程较小且需求的落点倾角绝对值也较小,应选择按低弹道飞行,因此有:
(13)
将需要速度分解至发射坐标系,可得:
(14)
为计算侧向需要速度,可假设火箭二级在K点处关机,经过时间TKM后侧向位置坐标恰好为ZM,于是有:
(15)
式中TKM为从K点到M点的飞行时间估计值。闭路制导计算公式为:
(16)
其中P,e,ξK,ξM根据式(4)~式(7)计算。
设火箭在K点处的实际速度为(VxK,VyK,VzK),则K点处的增益速度为:
(17)
为使火箭飞行速度尽快接近需要速度,火箭推力方向应与增益速度一致,于是俯仰、偏航导引指令为:
(18)
由上述指令计算过程可知,每个周期的制导解算一次完成,不需任何迭代,也不含专门针对耗尽关机的能量耗散处理。
4 仿真验证
4.1 仿真条件
探空火箭发射点海拔高度为1 000 m,经度为100°,地理纬度为40°,射向北偏西45°,理论落点在发射坐标系下的坐标为(500 000 m,-19 000 m,0 m),期望的落点弹道倾角为-35°。为综合补偿制导模型忽略惯性力、大气阻力等因素对落点位置的影响,虚拟目标点相对于理想落点的坐标修正量取为(-1 350 m,0 m,-750 m)。二级发动机点火时刻判断条件为rN-rK≤0,虚拟目标点处的倾角约束取-31.6°(考虑再入减速对弹道倾角的影响以及二级助推前后弹道平稳过渡两重因素)。闭路制导虚拟目标点处的速度大小设置为标况下不计再入大气阻力影响的弹头落地速度200 m/s。采用考虑地球自转和引力J2项摄动的六自由度仿真模型,在表1所示的主要参数散布条件下,进行1 000次蒙特卡洛随机打靶仿真。

表1 蒙特卡洛仿真主要参数散布
4.2 仿真结果
图3~图4分别绘出了前50次仿真二级点火前后弹道散布随射程的变化情况。受多重干扰组合影响,一级助推结束后的高度、侧偏散布呈逐步增大趋势,在二级点火前高度散布超过10 km,侧偏散布超过3 km。经过二级制导飞行后,高度、侧偏散布呈逐渐缩小的趋势,表明文中的制导控制方法能够适应火箭飞行过程中的各种干扰影响,有效修正弹道偏差。由于仿真时是以一级椭圆弹道与理想二级椭圆弹道的交点为二级点火时刻,因此二级点火位置在弹道纵平面内沿期望弹道分布仿真结果与设计相符。

图3 二级点火前后的高度散布变化

图4 二级点火前后的侧偏散布变化
图5~图6分别绘出了前50次仿真二级闭路制导期间姿态角指令随时间的变化情况。可见从二级点火到耗尽关机,俯仰角指令变化量小于8°,偏航角指令变化量小于4°,制导指令总体平稳,有利于简化的姿态控制系统控制实现。

图5 二级闭路制导俯仰角指令

图6 二级闭路制导偏航角指令
图7~图8分别给出了全部1 000次仿真的落点位置及弹道倾角散布。仿真落点弹道参数基本呈以期望值为中心的对称分布,其中位置偏差小于2.2 km,弹道倾角偏差小于0.5°,火箭落点位置及弹道倾角散布控制效果良好。

图7 落点位置散布
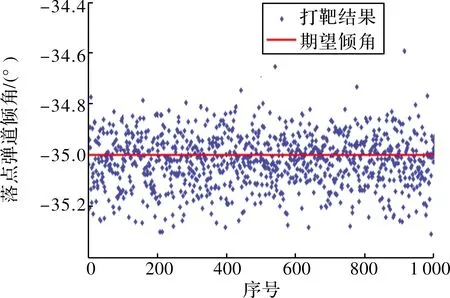
图8 落点弹道倾角散布
5 结论
提出了一种基于二级点火时刻控制与闭路制导相结合的探空火箭落点位置及倾角散布控制方法。该方法依据一级实飞椭圆弹道与二级期望椭圆弹道之间的相对位置关系进行二级点火时刻自适应控制,将地球自转等因素对弹道的影响综合视为系统性误差通过虚拟目标进行补偿,并采用给定较大虚拟目标速度的方式进行二级闭路制导。仿真结果表明:该制导方法简单、指令平稳、无需迭代计算和能量耗散,能够在耗尽关机的条件下较好克服火箭飞行过程中的各种干扰影响,实现较高精度的落点位置及弹道倾角控制,具有一定的工程实用价值。
