极端条件下大长径比固体发动机药柱结构完整性快速分析

余 瑞，张 路，何 君，吴 敏，唐承志，邓康清，郭 翔，庞爱民

(1 航天化学动力技术重点实验室，湖北襄阳 441003；2 湖北航天化学技术研究所，湖北襄阳 441003)

0 引言

固体火箭发动机在制造、勤务、发射和飞行的过程中，会受到固化降温、点火增压、冲击振动和飞行过载等载荷的作用，可能导致发动机药柱产生过大的应力和应变，造成发动机故障，因此有必要开展各种单一载荷或者组合载荷条件下的药柱结构完整性分析。随着军事需求和武器装备多样化发展，大部分战术导弹要求能在低温下工作，点火增压和低温环境的叠加作用使得药柱结构的完整性问题更加突出[1-4]。

除了外部载荷的作用因素，药柱结构完整性还和药形、长径比、马赫数及约束等内部结构特征相关。研究表明增加药形复杂度，增大长径比、马赫数，增强约束都会使得药柱的受力状况变差，对药柱的结构完整性不利[2-5]。在有些情况下，为了提高发动机的工作效能，通常采用复杂装药设计，例如大长径比、高马赫数、星形内孔或翼柱形串联装药等方式，进而达到各种技术、战术指标要求。这些药形结构复杂，尺寸不一，应力集中明显，结构危险点的位置也随整体药柱结构变化[5]，再加上外部组合载荷的叠加作用，对发动机的结构完整性提出了严峻的挑战。

针对固体推进剂药柱的粘弹性特性分析，国内外学者提出了多种粘弹性本构模型来反映药柱的真实力学响应[6-7]。Ho等认为在瞬态冲击条件下药柱产生的应变和应力线性相关[8]，提出的线粘弹性本构模型可宏观反映粘弹材料的力学特性。多名学者应用线粘弹性本构模型研究了推进剂材料参数[9-11]、药柱几何参数[12-13]、侵蚀效应[14]对点火增压瞬态药柱结构力学响应的影响。虽然基于线粘弹性本构模型的仿真分析方法可以得到不同时刻药柱内部的结构力学响应，但不能直观得到任意时刻药柱等效模量的变化情况，且计算时间较长[15]。

文中针对某型大长径比复杂装药结构开展了药柱结构完整性分析，得到了极限温度条件下点火增压过程药柱结构的应力-应变响应，为结构完整性评估提供理论指导。为进一步提高计算效率，对点火增压下药柱结构完整性的快速评估方法进行二次开发，编写了点火增压药柱结构完整性快速评估程序，并应用该程序分析得到关键位置极端温度点火增压过程中固体火箭发动机的结构响应，将分析结果与基于线粘弹性本构模型的有限元仿真分析结果进行对比，验证了该快速评估程序的准确性，为极端温度点火增压过程中实际固体发动机药柱结构完整性的快速分析提供参考。

1 理论模型和计算方法

1.1 线粘弹性本构模型

一般情况下，积分型线粘弹性本构模型适用于线性粘弹性材料的有限元数值计算，在较小应变情况下可用来表征固体推进剂的力学性能[16]，积分型线粘弹性本构模型的三维形式为：

(1)

式中：eij为应变偏张量的对应原素；εkk为应变球向量的对应原素；δij为克罗内克符号(若i=j,则δij=1;否则为0)；ξ,ξ′为等效时间，其定义为：

(2)

式中，αT为温度-时间转换因子。剪切松弛模量G(t)、体积松弛模量K(t)可表示为：

(3)

式中:υ为泊松比；E(t)为松弛模量。

1.2 点火增压过程中药柱结构完整性快速评估方法

对于确定的固体发动机以及推进剂，药柱受到阶跃内压力作用时的等效应变仅与压力和松弛模量有关[17]。药柱受到阶跃内压力作用时的等效应变可表示为[15]:

ε(t)/Pi=Sp1/E(t)+Sp2

(4)

式中，Sp1,Sp2为药柱的压力应变系数。对于简单圆管形装药发动机药柱，可得到Sp1,Sp2的解析解[17]。对于复杂的发动机，无法得到Sp1,Sp2的解析解，但通过有限元软件计算得到药柱在不同恒定压力载荷下的应变大小，通过拟合可得到压力应变系数。

设点火增压过程中，温度为T，增压载荷为P(t)=P0(1-eλt)，将增压时间t划分成n份，在误差允许范围内，分段的压力阶跃函数可代替真实的增压函数。由式(4)知，每阶跃增加压力ΔPi，产生的应变Δεi和应力Δσi为[15]：

Δεi=ΔPi(Sp1/E(tn-ti-1,T)+Sp2)

(5)

Δσi=E(tn-ti-1,T)Δεi

(6)

设推进剂在参考温度Ts时的松弛模量为E(t，Ts)，实验得到推进剂在参考温度Ts时的WLF(Williams-Landel-Ferry)方程为：

(7)

式中，C1,C2为常数。

T温度下t时刻的等效模量和时间为：

E(t,T)=E(ξ,Ts)

(8)

(9)

t时刻药柱总应变ε(t)和总应力σ(t)的表达式为：

(10)

(11)

t时刻药柱的等效模量可表示为：

Eeq(t)=σ(t)/ε(t)

(12)

2 发动机性能参数

2.1 发动机有限元模型

以某翼柱形装药固体火箭发动机为研究对象，结构由壳体、绝热层、前后人工脱粘层和药柱组成，燃烧形式为内孔燃烧，其中圆管段药柱的长径比约为16.6，马赫数约为3.7，星形段含有8个星角，肉厚e1=6 mm，根据药柱结构的对称性，对发动机的1/16进行仿真分析，共生成242 411个节点，52 706个单元，三维模型如图1所示。

图1 发动机三维模型示意图

2.2 载荷及边界条件

1)载荷工况

固体火箭发动机分别在高温(60 ℃)和低温(-40 ℃)下进行点火试验，点火增压过程中，燃烧室内部压力经过约0.1 ms达到峰值8 MPa，假设增压过程中药柱受压均匀，内压载荷表示为：

P(t)=8(1-e-60t)

(13)

式中：P为内压；t为时间。

2)边界条件

依据实际发动机的设计情况，认为壳体与绝热层、绝热层与药柱接触界面之间粘接牢固。前、后人工脱粘层及内孔表面为自由表面。内压载荷作用在发动机内部自由表面，同时在对称面上施加相应的对称约束，对发动机壳体头部施加位移约束。

由于增压时间极短，燃烧室的温度还来不及传导至推进剂中，因此假设点火增压过程中药柱温度不发生变化。

2.3 力学性能参数

固体发动机各部件的基本力学性能参数如表1。

表1 发动机材料基本力学参数

固体发动机药柱为丁羟体系配方，泊松比为0.495，线膨胀系数为9.9×10-5K-1，对该配方推进剂在各种温度下的松弛模量进行拟合，得到推进剂相对模量和松弛时间如表2。

表2 推进剂相对模量和松弛时间[18]

已知，固体推进剂的零应力温度为60 ℃，通过实验得到推进剂在参考温度Ts=273.15 K时C1=13.97，C2=253.7。

为确定在压力载荷作用下发动机药柱的受力危险部位，选取恒定压力载荷，得到了药柱的应力应变分布。计算结果显示药柱的危险位置集中在后翼槽顶部位置，药柱最大等效应力、应变位置如图2所示。

图2 药柱最大等效应力、应变位置

在确定危险位置后，由式(4)可知，计算两种不同压力载荷和药柱模量条件下的等效应变，即可求得危险位置的压力应变系数。这里选取恒定压力为8 MPa，药柱弹性模量分别为5 MPa和10 MPa，对固体发动机进行线粘弹性仿真分析，得到该位置的等效应变分别为0.408 66和0.222 93。将以上数据代入式(4)得到药柱的压力应变系数Sp1,Sp2，从而压力应变方程为：

εeq(t)/Pi=0.2322/E(t)+0.004650

(14)

3 药柱结构完整性快速评估程序

针对点火增压过程中药柱结构完整性快速评估问题进行程序开发，程序流程如图3所示。通过输入药柱材料参数、载荷以及拟合得到的药柱压力应变系数可实现药柱结构完整性的分析。应用该评估界面可快速得到点火增压过程中药柱内关键位置的等效时间、等效模量、等效应力和等效应变的变化情况。

图3 点火增压过程药柱结构完整性快速评估流程图

4 计算结果与分析

为了分析增压载荷对药柱结构完整性的影响，点火增压过程中不考虑环境温度变化，分析时认为固体发动机的整体温度分布均匀且和环境温度一致。首先，应用ANSYS Workbench基于线粘弹性本构模型对药柱进行分析，得到药柱的结构响应；然后，应用点火增压过程药柱结构完整性快速评估程序，计算得到极端温度(60 ℃、-40 ℃)下药柱内危险位置的等效应变、等效应力和等效模量；最后，将两种计算结果进行对比分析。

4.1 高温点火增压过程中药柱结构完整性分析

药柱和环境温度均为60 ℃,仿真分析得到药柱内部应力应变分布，药柱在0.1 s时的等效应变、等效应力分布场如图4所示。有限元计算和开发的评估程序分析得到的药柱等效应变、等效应力和等效模量随时间变化情况分别如图5、图6所示。

图4 60 ℃点火增压至0.1 s时药柱等效应变应力场

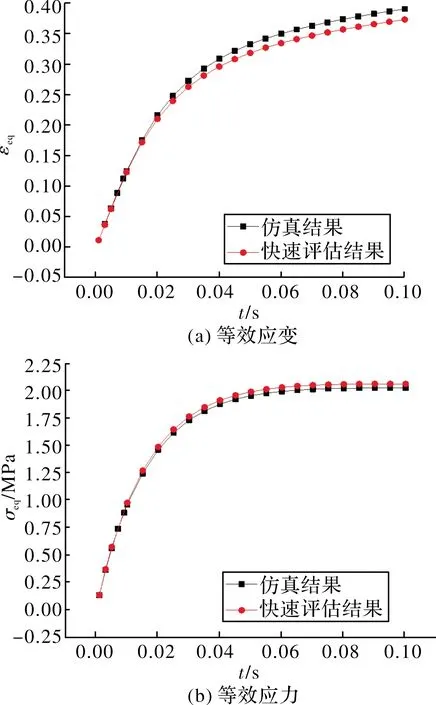
图5 60 ℃点火增压过程中药柱危险位置应变应力曲线

图6 60 ℃点火增压过程中药柱等效模量曲线

由图4～图6可知，高温(60 ℃)点火增压过程中：1)药柱的危险位置主要集中在圆管段内表面和翼柱交接过渡处，最大等效应力、应变发生在翼形和圆柱段交界处；2)药柱的等效应力应变随着内压力载荷的增加而增加，在压力达到峰值时最大，药柱的等效模量随着增压时间逐渐松弛；3)有限元计算和开发的评估程序分析得到的药柱危险位置等效应变、等效应力和等效模量曲线基本重合。

4.2 低温点火增压过程中药柱结构完整性分析

药柱和环境温度均为-40 ℃，低温点火增压过程中仿真分析得到药柱在0.1 s时的等效应变、等效应力分布场如图7所示，仿真计算和快速评估得到的药柱危险位置等效应变、等效应力和等效模量的变化情况分别绘制在图8、图9中。

图7 -40 ℃点火增压时药柱内部等效应力应变场

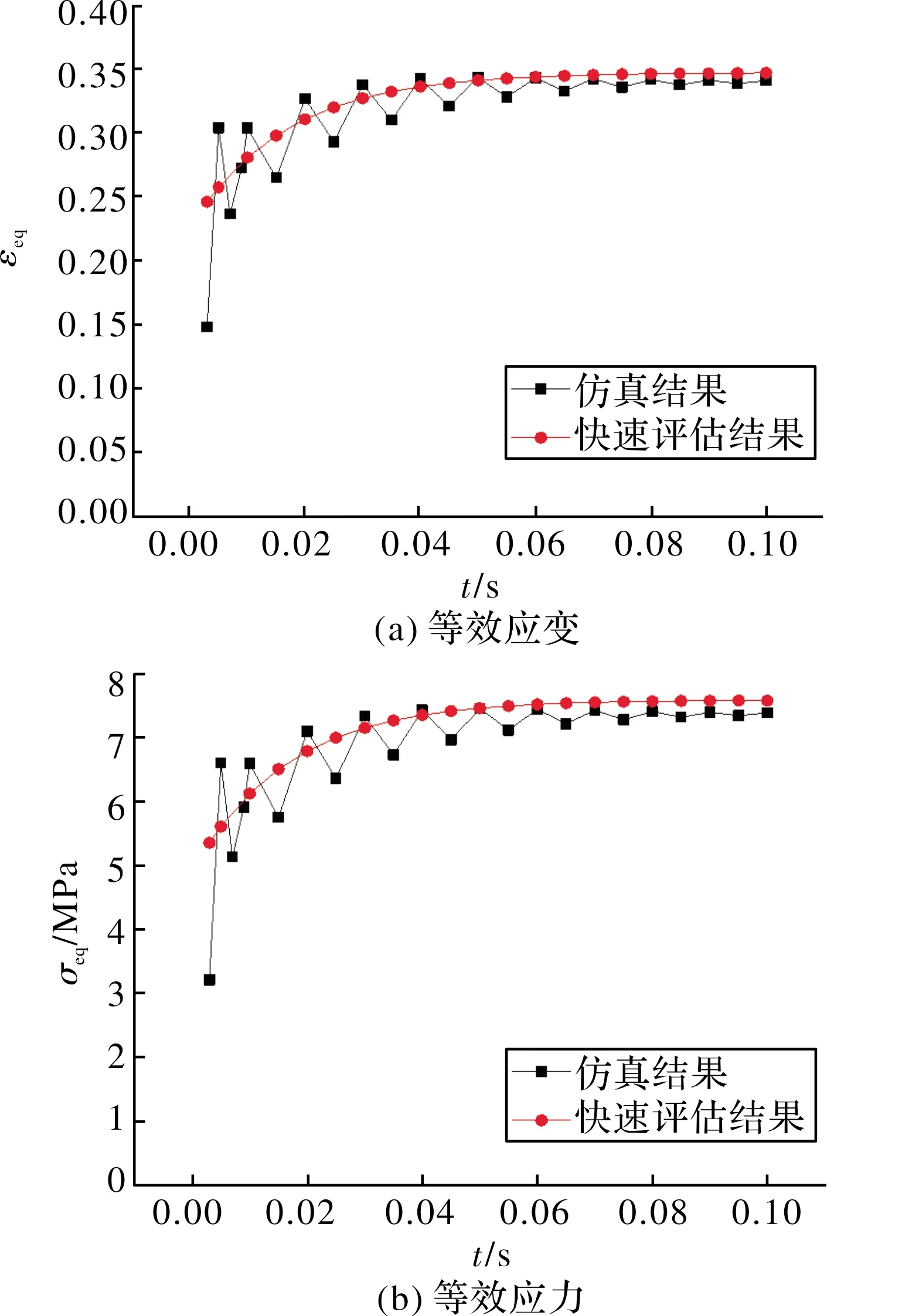
图8 -40 ℃点火增压过程快速评估界面

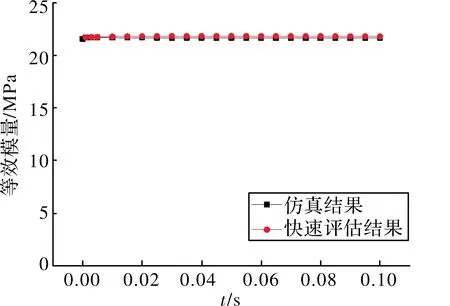
图9 -40 ℃点火增压过程中药柱等效模量曲线

由图7～图9可知，低温(-40 ℃)点火增压过程中得到的药柱危险位置与高温(60 ℃)情况下得到的结果一致。同时仿真计算和快速评估得到的结果变化趋势一致，误差较小。

4.3 计算结果统计与分析

由以上计算结果可知，高温(60 ℃)和低温(-40 ℃)下点火增压过程中两种计算方法得到的危险位置等效应变、等效应力和等效模量最大值发生在0.1 s，因此分别采用快速评估程序和有限元分析两种方法计算了0.1 s时刻危险位置的力学响应，对比结果见表3。其中需要说明的是，快速评估的计算时间包含压力应变系数确定前的仿真分析、拟合时间和系数确定后评估程序运行时间。

由表3可知，两种方法计算结果比较吻合，误差在4%以内。其中高温最大等效应变为0.382，低温最大应变为0.341, 均小于药柱的极限应变，能够满足结构完整性的要求。同时采用快速评估程序计算时间明显减少，大大提高了计算效率。结果证明该快速评估程序可实现对极端条件下大长径比复杂固体发动机药柱结构完整性的快速分析。

表3 计算结果统计与分析对照表

5 结论

1)针对大长径比翼柱形装药结构开展了药柱结构完整性分析，得到了极限高低温条件下点火增压过程药柱应力-应变的分布规律。结果表明药柱内孔和翼柱交界面是应力集中区域，最大位置位于翼形和圆柱段交界处。并通过计算得到了危险位置的力学响应，为药柱结构完整性分析提供理论指导。

2)建立了极端温度下点火增压过程固体发动机药柱危险位置结构完整性的快速评估方法，得到了等效应力、应变、模量和压力应变系数的具体函数表达形式，并利用C#语言二次开发了极端温度下点火增压过程中药柱结构完整性快速评估程序。

3)应用该程序对极端条件下某翼柱形固体发动机药柱的结构完整性进行分析，分析结果与基于粘弹性本构模型的有限元仿真结果吻合很好，且基于该程序的计算所需时间大大减少，验证了快速评估程序的适用性。