基于简化多重渐消因子强跟踪CKF的SINS非线性初始对准算法

彭志颖, 夏海宝，卢 航，郝顺义，黄国荣

(空军工程大学航空工程学院, 西安 710038)

0 引言

SINS的实际工作环境通常比较复杂且具有较大的不确定性，SINS粗对准的结果为大失准角，此时基于小失准角假设的线性误差模型和卡尔曼滤波方法已不再适用，文献[1]采用由欧拉平台误差角(EPEA)描述的非线性误差模型和非线性滤波算法来解决这个问题，但因为系统会受到模型误差、噪声以及外界扰动等影响，非线性滤波存在鲁棒性不佳和跟踪能力差的问题[2-3]。文献[4]提出了强跟踪滤波理论，强跟踪滤波在面对模型不确定性、噪声、外界干扰较大的情况下可以保持较强的模型失配鲁棒性和跟踪能力[4-6]。文献[3]将强跟踪UKF应用于初始对准，但系统中每个状态变量的不确定性互不相同，采用单一渐消因子无法保证对每个状态变量都进行较好的跟踪。文献[7]提出了多重渐消UKF滤波(MSTUKF)算法无需计算EKF中繁琐的雅克比矩阵。现有理论已经证明[8-10]，UKF精度达到二阶，CKF精度可以达到三阶，并且CKF无需多的采样点和调整的参数，具有更短的滤波时间和更可靠的数值稳定性。

文中根据三阶球面-径向容积准则中容积点的分布特征和量测方程为线性的模型特点，推导了简化CKF(RCKF)，并将STF理论和RCKF算法框架相结合，引入两个多重渐消因子阵，提出一种适用于初始对准的简化多重渐消因子强跟踪CKF算法(RMSTCKF)，整个滤波算法只需计算一次容积变换，无需计算雅各布矩阵，同时多重渐消因子可以根据不同状态的不确定性程度大小相应提高各个状态的跟踪能力。文中采用文献[1]中由EPEA描述的SINS非线性误差方程并推导了非线性滤波方程，通过系统噪声不匹配和基座受扰动情况下的仿真实验，结果验证了RMSTCKF的有效性。

1 多重渐消因子强跟踪滤波器

STF原理是通过在预测协方差矩阵Pk|k-1中引入一个多重渐消因子阵λk，达到在线调整增益矩阵Kk的目的，滤波器需要满足2个条件[7]：

(1)

式(1)使得滤波器满足最小方差估计的性能指标。式(2)强迫滤波器的残差序列时刻保持正交，克服了滤波器在遇到模型不确定或者状态突变等情况时，因为残差序列不正交，导致滤波器性能下降的问题[4-5]，使得强跟踪滤波器对模型不确定性有较强的鲁棒性，对状态突变有较强的跟踪能力。

1.1 RMSTCKF算法流程

RMSTCKF算法流程如1)～10)所示，其中1)～4)为时间更新，5)～10)为量测更新。

1)计算容积点Xi,k-1|k-1,i=1,2,…,2n。

(2)

(3)

3)计算当前时刻的状态估计值。

(4)

(5)

(6)

对于量测方程为线性的CKF来说，可以在其量测更新中进行简化，下面给出简化CKF量测更新的推导过程。

(7)

(8)

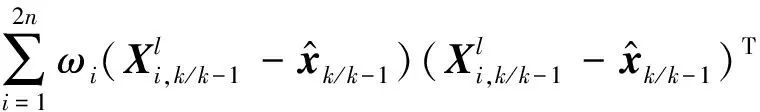
(9)

(10)

(11)

10)当前时刻k的滤波状态值。

(12)

(13)

在Pk/k-1中引入两个多重渐消因子阵代替传统的单渐消因子，形式如下：

(14)

1.2 RMSTCKF中多重渐消因子的次优求解算法

多重渐消EKF的多重渐消因子阵次优解法如下[2]：

(15)

(16)

(17)

(18)

(19)

(20)

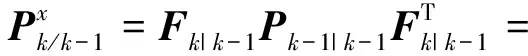
(21)

(22)

此时Mk、Nk可以表示为：

(23)

(24)

其中Hk即为量测矩阵。将式(23)、式(24)分别代入式(17)、式(18)，即可得到多重渐消因子阵次优解法。

2 大方位失准角误差模型

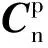
(25)

2.1 SINS姿态误差方程

(26)

(27)

(28)

2.2 SINS速度误差方程

理想条件下，捷联惯导的速度微分方程如下

(29)

然而在实际工作时，捷联惯导系统所计算的速度微分方程：

(30)

(31)

2.3 SINS非线性滤波模型

(32)

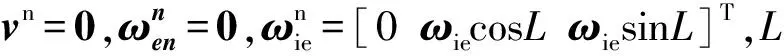
(33)

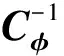
(34)

将式(28)、式(31)、式(34)代入式(33)，整理并忽略二阶及二阶以上小量即可得到大方位失准角滤波模型,这里不再详细写出具体表达式。

3 数值仿真与分析

将RCKF、RSTCKF、RMSTCKF滤波算法用于大方位失准角滤波模型进行初始对准仿真。SINS位置取北纬45°，东经108°，高度100 m处，系统的初始状态X0=0，惯性测量组件参数如表1所示。

表1 惯性测量组件主要性能参数

初始方差阵P(0)、系统噪声阵Q、量测噪声阵R，设置为：

P(0)=diag[(2°)2(2°)2(10°)2(0.1 m/s)2(0.1 m/s)2(100 μg)2(100 μg)2(0.1°)2(0.1°)2(0.1°)2]

Q=diag[(0.05°/h)2(0.05°/h)2(0.05°/h)2·

(50 μg)2(50 μg)2(50 μg)205×1]

R=diag[(0.1 m/s)2(0.1 m/s)2]

3.1 静基座初始对准仿真

设置SINS东向、北向、天向的初始失准角为φ=[1° 1° 30°]T，应用上述3种滤波算法进行600 s的初始对准仿真，天向失准角误差曲线(经过开环滤波修正的航向角减去真实航向角)如图1所示。在收敛精度方面，RCKF、RSTCKF、RMSTCKF三种滤波算法精度差别不大，通过100次Monte-Carlo仿真，初始对准精度用最后100 s方位失准角误差的算术平均值来衡量，3种算法的具体结果如表2所示。在收敛速度方面，RMSTCKF在120 s左右收敛至极限精度附近，稍快于RSTCKF和RCKF。在理想环境下，系统没有受到模型误差和外界扰动的影响，残差序列时刻保持正交，3种滤波器始终可以保持较高的滤波性能。

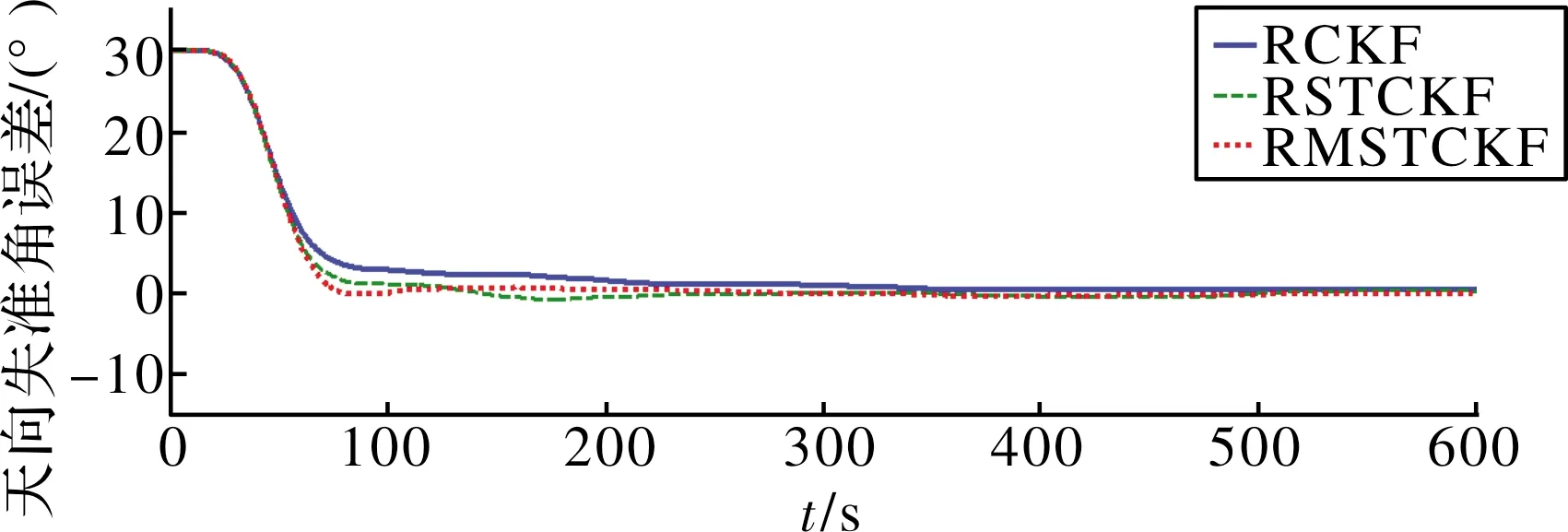
图1 3种滤波算法所得失准角误差

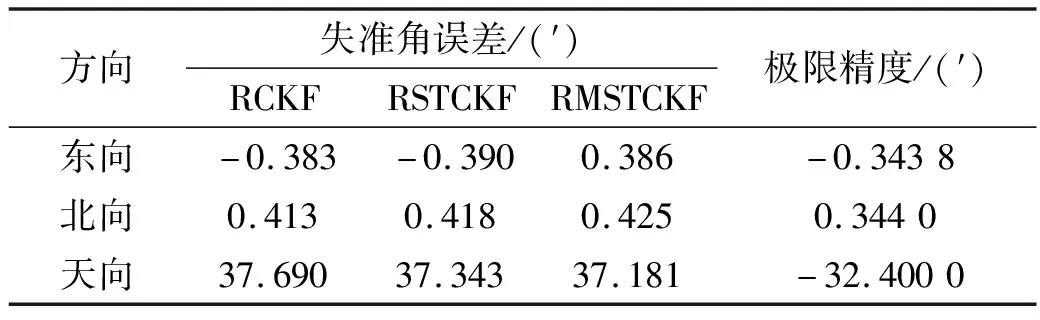
表2 3种滤波算法对准结果比较

3.2 系统噪声方差阵不匹配初始对准仿真

为了检验提出的RMSTCKF算法的适应性和鲁棒性，将系统真实的噪声协方差阵扩大9倍，滤波模型中Q的设定值不变，天向失准角误差曲线如图2所示。当系统噪声不匹配时3种算法均收敛，600 s的滤波值分别为192.36′、39.12′、38.64′。RCKF波动最为明显，400 s后波动才逐渐消失，收敛速度和精度均较差；RSTCKF和RMSTCKF表现明显优于RCKF，但RSTCKF也存在较小的扰动，两者均可以很快收敛至极限精度附近。

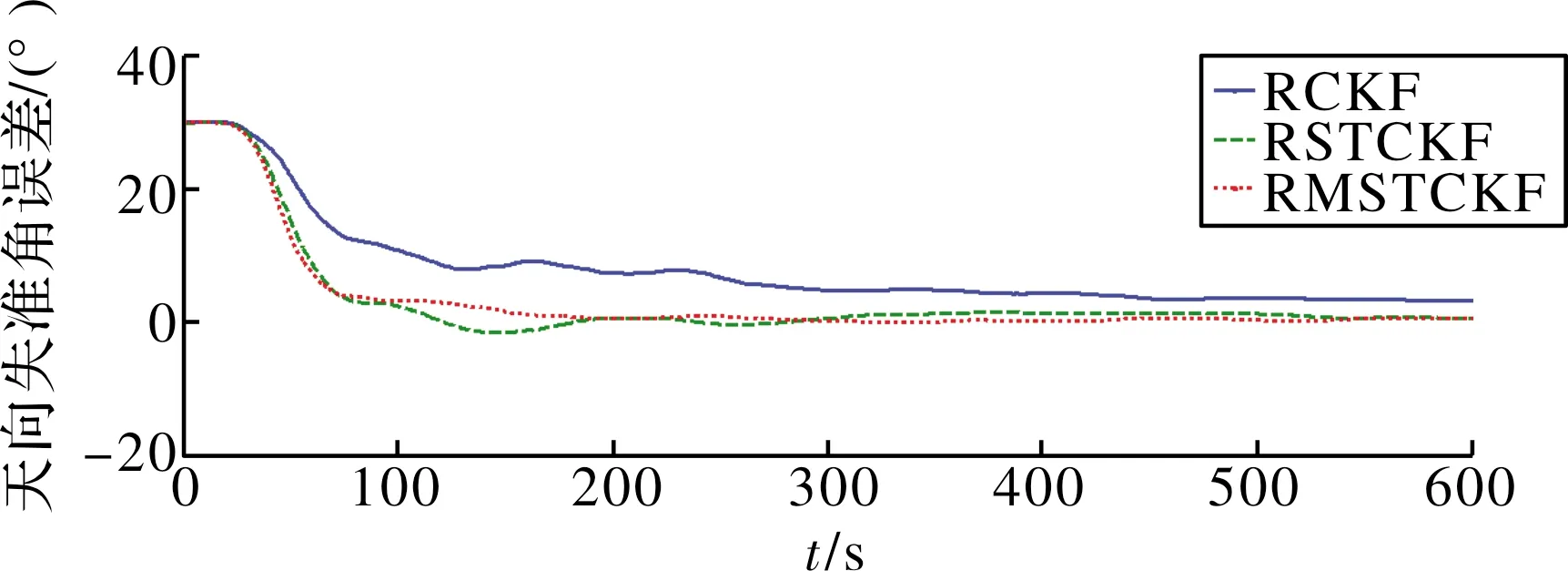
图2 系统噪声不匹配3种滤波算法所得失准角误差

3.3 基座扰动时初始对准仿真

SINS静基座初始对准仿真并没有考虑实际惯导系统工作时常遇到的外界扰动等因素。为检验RMSTCKF在遇到外界扰动时的鲁棒性与跟踪性，当对准时间达到40 s时，在基座原点处加入沿俯仰角和横滚角时长为10 s(40～50 s)的正弦晃动干扰：

(35)

其余的仿真条件不变，用上述3种滤波方法进行600 s的初始对准仿真实验，天向失准角误差曲线如图3所示，其中图3(b)为图3(a)在受扰处的放大图。

从图3(a)中可以看出，系统受到扰动后，RMSTCKF和RSTCKF相较于RCKF具有更强的调节能力和更短的收敛时间，其中RMSTCKF在150 s左右收敛到极限精度附近，RSTCKF在220 s左右收敛至极限精度附近，RCKF在受到扰动后调节能力较差，500 s左右才收敛至极限精度附近。

图3 存在一次突然扰动时3种滤波算法的失准角误差

从图3(b)中可以看出，在40 s到50 s受扰动期间，3种算法的滤波值都因为受扰而产生不同程度的波动。其中RMSTCKF波动明显小于另外两种算法，说明该算法在状态突变时具有较强鲁棒性和跟踪性；RSTCKF受扰动后的波动要大于RMSTCKF，小于RCKF。RCKF的波动最大，滤波性能在受扰后明显下降，无法满足SINS的对准要求。为了进一步检验RMSTCKF的滤波性能，在滤波进行到105 s时继续在基座原点处加入沿俯仰角和横滚角时长5 s的正弦晃动扰动以增加系统的复杂程度和不确定性。天向失准角误差曲线如图4所示。

图4 存在两次突然扰动时3种滤波算法的失准角误差

由图4可知，当系统受到二次扰动后，3种滤波算法的性能受到了不同程度影响，RMSTCKF在受扰后100 s左右就可以迅速收敛至稳态，具有较快的过渡过程；RSTCKF的波动略大于RMSTCKF，在受扰后120 s左右收敛至稳态；RCKF对准时间大于600 s，对准精度大大下降。

结合图3和图4分析可知，当系统受到扰动后，RMSTCKF具有比RSTCKF和RCKF更强的跟踪能力和鲁棒性。这是因为RMSTCKF的多重渐消因子在面对模型不匹配和外界干扰时可以用不同的渐消速率对不同的状态进行估计，更加准确的调节增益矩阵，以保证每个状态的滤波性能，具有更好的自适应性和滤波精度。

4 结论

文中提出了一种适用于大方位失准角初始对准的RMSTCKF算法，给出了该算法的计算流程和多重渐消因子阵的次优求解法，推导建立了用欧拉平台误差角表示的SINS非线性误差方程，并在静基座、系统噪声方差阵不匹配、基座受扰动3种情况下利用RCKF、RSTCKF、RMSTCKF三种滤波算法进行了大方位失准角初始对准仿真。结果表明，提出的RMSTCKF对于系统噪声方差阵不匹配的情况具有较强的自适应能力；当系统受外界扰动时，RMSTCKF表现出较强的鲁棒性和强跟踪能力，与另两种滤波算法相比，RMSTCKF具有更强的工程实用价值。