导弹纵向平面部分制导控制一体化设计方法

安 通，王建华，潘玉龙，陈海山

(1 空军预警学院，武汉 430019；2 战略支援部队航天工程大学，北京 101400)

0 引言

导弹俯冲段运动具有快时变、强非线性和不确定性的特点，加之导弹质心运动和绕质心运动之间存在一定耦合，使得传统的基于频谱分离的制导控制系统设计方法难以满足性能要求[1]。制导与控制一体化(integrated guidance and control, IGC)设计方法能够充分考虑制导与姿态控制分系统的耦合特性，从而提高制导控制系统的性能，目前已被广泛研究和应用[2-3]。

针对导弹纵向平面内IGC设计问题，目前最常用的思路是建立同时包含视线倾角、攻角和俯仰角速率等制导控制系统被控状态的全状态耦合IGC设计模型，且模型具有严格反馈形式，然后再利用反演控制方法求解，从而将IGC系统设计问题转化为非线性时变系统的输出调节问题[4-5]。动态面控制方法在反演控制方法基础上引入一阶低通滤波器。基于该方法，许多学者开展了导弹纵向平面内IGC系统设计的研究，并针对设计模型中存在的不确定项，利用自适应技术[6]、模糊控制技术[7]和干扰观测器技术[8-9]等方法进行补偿。然而上述方法普遍存在设计过程复杂、设计参数较多的问题。此外还有学者利用滑模控制[10]、预测控制[11]和最优控制[12]等方法开展导弹纵向平面内IGC系统设计。

部分制导控制一体化(partial integrated guidance and control, PIGC)方法通过建立相对运动模型中的飞行器加速度分量与飞行器三通道角速率之间的解析模型，完成双环路控制结构的设计，能够有效降低制导控制系统的阶数，提高制导控制系统的集成度，已被应用于各类飞行器[13-14]。目前已有研究者将PIGC方法应用于导弹纵向平面内制导控制系统设计，如Wang等应用终端滑模控制方法设计了导弹纵向平面内PIGC系统，外环生成俯仰角速率指令，内环设计俯仰舵偏角以跟踪角速率指令，设计方法的有效性也通过仿真得到了验证[15-16]。然而，目前关于面向工程应用实际的导弹纵向平面内PIGC系统设计的研究成果仍然较少，且俯仰角速率与导弹加速度分量之间的解析关系也有待进一步探究扩展。基于此，文中针对导弹俯冲段纵向平面内制导控制系统设计问题，建立一种新的基于导弹加速度分量的俯仰角速率解析模型，并应用滑模控制理论和动态面控制中的一阶低通滤波器思想，提出纵向平面内PIGC设计方法。该方法具有系统模型阶数少、设计流程简单、便于工程应用的优点，可进一步丰富和完善导弹纵向平面制导控制系统设计理论。

1 导弹俯冲段运动建模

1.1 纵向运动模型

为了便于问题研究，在建立导弹俯冲段纵向运动模型时忽略地球自转和地球曲率的影响，导弹纵向运动模型为：

(1)

式中：v为导弹飞行速率;P为导弹推力;m为导弹质量;g为重力加速度;θ为速度倾角;D,L分别为导弹所受的气动阻力和气动升力;α为飞行攻角;x,y为导弹在地面坐标系[17]中的坐标分量;ωz为导弹俯仰角速率;Jz为导弹俯仰转动惯量;Mz为作用在导弹上的俯仰气动力矩。导弹气动模型具体形式为：

(2)

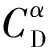
1.2 相对运动模型

图1给出了导弹-目标相对运动几何示意图，OB代表导弹质心，T代表地面目标位置。OB-xsyszs为视线坐标系[17]，O-xyz为地面坐标系，设定地面坐标系原点所在经度和纬度均为0°，所在高度为0 m，x轴正方向指向正东，y轴正方向垂直于地面且向上，λD为视线倾角，λT为视线偏角。基于三维相对运动模型，导弹纵向平面内相对运动方程可简化为[4]：

图1 相对运动几何示意图

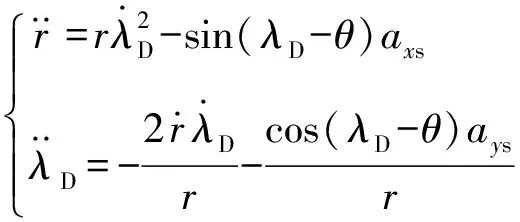
(3)

式中：r为导弹与目标位置的相对距离;axs、ays为导弹加速度在视线坐标系轴上的分量。

2 导弹PIGC系统设计

2.1 俯仰角速率解析模型

由导弹纵向运动模型可知，纵向平面内导弹在地面坐标系中的速度矢量与在弹体坐标系[17]中的速度矢量满足：

(4)

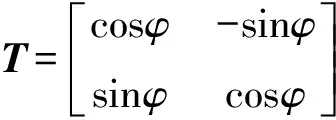
(5)

(6)

式中：B=[-sinφu-cosφvcosφu-sinφv]T。进一步可以得到基于导弹加速度分量的俯仰角速率解析模型为：

(7)

2.2 PIGC设计

(8)

式中：ε1,ρ1和k1为待设计参数。联立式(3)和式(8)，可以得到导弹加速度在视线坐标系轴上分量的指令值为：

(9)

由坐标系转换关系可知，ays与[axhayh]T满足：

(10)

记C=[-sinλDcosλD]A，联立式(9)和式(10)，可得到纵向平面内导弹在弹道坐标系中加速度的指令值为：

(11)

联立式(7)和式(11)，可以得到俯仰角速率指令为：

(12)

考虑到在姿控分系统设计过程中需要用到俯仰角速率指令的变化率，而直接对俯仰角速率指令进行求导会增加制导控制系统的计算量，在工程上也不便实现，因此引入动态面控制中的指令滤波思想，将制导分系统生成的指令值通过一个一阶低通滤波器：

(13)

式中：τ为滤波器常数;ωz,d为ωz,c的滤波值，也是制导分系统最终生成的俯仰角速率指令。

下面对俯仰角速率指令生成的机理进行简要说明：首先基于滑模控制方法，设计导弹加速度在视线坐标系轴上分量的指令值ays,c，然后通过广义逆运算实现该指令值在axh,c与ayh,c上的分配，再利用推导的俯仰角速率解析模型，生成俯仰角速率指令，最后将该指令通过一阶低通滤波器，得到制导分系统生成的俯仰角速率制导指令及其变化率。

接下来设计姿控系统，跟踪制导分系统生成的俯仰角速率指令值。应用滑模控制方法，设计滑模面S2=ωz-ωz,d，并选取滑模趋近律为：

(14)

式中：ε2,ρ2和k2为待设计参数。基于式(1)和式(2)，导弹绕质心动力学方程可整理为：

(15)

联立滑模面函数S2、式(14)和式(15)，可以直接生成俯仰舵偏角指令为：

(16)

PIGC方法设计完毕。

该设计方法中，制导分系统基于导弹-目标相对运动参数和导弹运动参数，直接生成俯仰角速率指令及其变化率，姿控分系统基于滑模控制理论跟踪俯仰角速率指令并生成俯仰舵偏角指令，制导控制系统的模型阶数仅为2，且设计参数较少，设计流程得到了简化，更便于工程应用。

3 仿真实验

面向纵向平面内导弹俯冲攻击地面目标任务，通过仿真实验，验证所设计的PIGC方法的有效性和鲁棒性。导弹模型参数标称值如表1所示[17]。

表1 导弹模型参数

考虑到导弹气动舵实现能力，舵偏角被限定在±30°内，且最大变化率为100°/s。为方便问题研究，将地面目标视为质点。当导弹所在高度小于0 m时，仿真终止，仿真终止时刻导弹与目标之间的距离即为脱靶量。此外，当导弹-目标相对距离小于30 m时，导引头进入盲区，PIGC系统不再工作，即俯仰舵偏角不再变化直至仿真结束。

3.1 有效性校验

首先在大气密度、气动力系数和气动力矩系数处于标称条件下，仿真验证所设计的PIGC方法的有效性。为了比较该PIGC方法与常规IGC设计方法之间的性能差异，将仿真结果与文献[17]提出的基于动态面的IGC设计方法进行对比，导弹的初始质心/绕质心运动参数和地面目标位置坐标的设置与文献[17]相同，即导弹初始运动参数设置为：v0=200 m/s，θ0=0.01 rad/s，xm,0=0 m，ym,0=3 000 m，φ0=0.03 rad，ωz,0=0.1 rad/s；地面目标位置坐标设置为：xt,0=3 000 m，yt,0=0 m。PIGC系统设计参数为：ε1=0.01，ε2=0.1，k1=0.1，k2=1，ρ1=ρ2=0.6，τ=0.1。

图2给出了导弹俯冲段的质心运动参数变化曲线。由图2(a)可以看出，两种方法下导弹飞行速度均随时间增大。由图2(b)和图2(c)中可以看出，与IGC方法相比，PIGC方法下导弹的速度倾角调整过程更为缓慢，弹道更加弯曲。

图2 导弹质心运动参数变化曲线

图3给出导弹-目标相对运动参数的变化情况。由图3(a)可知，与IGC方法相比，PIGC方法下视线倾角调整过程更为缓慢，这与图2(b)中的速度倾角变化规律相一致。由于视线倾角是根据导弹和地面目标的相对空间位置计算得到的，因此终端时刻的视线倾角会急剧变化。PIGC方法和IGC方法下导弹终端脱靶量分别为0.15 m和0.21 m，说明两种方法下导弹均可以精准命中地面目标。

图3 相对运动参数变化曲线

图4给出了导弹实际俯仰舵偏角变化曲线，结果表明两种方法下实际俯仰舵偏角均光滑有界，且PIGC方法更加节约舵偏量。需要说明的是，基于文献[17]的IGC方法在计算实际舵偏量时并未考虑舵偏角变化率的限制，这使得在IGC方法下，仿真一开始俯仰舵偏角便可以直接达到+30°满偏。在更大的舵偏量作用下，导弹速度倾角和视线倾角得以迅速调整到某一常值附近，使得导弹俯冲轨迹更为平直。而文中提出的PIGC方法在解算实际俯仰舵偏角时考虑到了舵偏角变化率的限制，更加符合工程实际，且实际俯仰舵偏角在更小范围内缓慢变化也使得在该方法下导弹弹道更为弯曲。

图4 俯仰舵偏角变化曲线

图5给出了导弹绕质心运动参数的变化曲线，可以看出两种方法下导弹姿态变化均平稳有界，且PIGC方法下导弹的攻角和俯仰角速率的变化幅度均小于IGC方法，即导弹可以以更小姿态变化完成俯冲攻击任务。

图5 导弹绕质心运动参数变化曲线

3.2 鲁棒性校验

为了进一步验证设计的PIGC方法对参数偏差的鲁棒性，在大气密度、气动力系数和气动力矩系数处于偏差状态下开展仿真试验。在上节初始运动参数设置基础上，将导弹初始速度提高到400 m/s(超声速)，将初始高度提高到6 000 m，地面目标位置坐标设置为xt,0=6 000 m。将大气密度、气动力系数和气动力矩系数的标称值分别乘以1+0.2sint,1+0.3sint,1+0.4sint作为实际仿真参数，开展3种参数偏差条件下的仿真验证,仿真结果如图6所示。

图6 不同参数偏差条件下的导弹典型运动参数仿真曲线

可以看出随着偏差极限从图6(a)到图6(c)逐渐增大，各运动参数变化的波动程度也逐渐增大，但均有界平稳变化。此外受参数偏差极限的影响，图6(c)下导弹的俯冲轨迹明显与图6(a)和图6(b)偏差较大。图6(a)～图6(c)下导弹终端脱靶量分别为0.04 m、0.17 m和0.26 m，说明PIGC方法能够克服参数偏差的影响，使导弹命中地面目标，具有较好的鲁棒性。

4 结论

针对导弹俯冲段纵向平面制导控制系统设计问题，通过建立一种全新的俯仰角速率解析模型，设计了一种PIGC方法。该方法在外环生成俯仰角速率指令的过程中能够直接利用导弹在弹体坐标系中的加速度信息，并引入了动态面控制中的低通滤波器思想，因而更加便于工程实际应用。此外，该方法与常规的基于动态面的IGC设计方法相比，具有设计参数更少、模型阶数更低、更加节省舵偏执行量和导弹姿态变化幅度的优点。为导弹纵向平面制导控制系统设计提供了一种新的思路，在制导控制系统设计中并未考虑各项约束的影响，相关问题有待后续进一步研究。