基于图神经网络的高温树脂材料预测模型

2022-01-09胡航语

功能高分子学报 2021年6期

杨宁，魏伟，胡航语，郭雷，方俊

（西北工业大学 1.自动化学院; 2.计算机学院，西安 710129）

在材料信息领域，大部分研究主要针对树脂等高分子材料的制备以及性能[1-3]，而较少通过机器学习方法研发高分子新材料。基于机器学习方法的材料性能预测，已经在新材料研发领域体现出独特优势，能够有效地预测潜在的高分子材料性能，部分替代第一性原理的运算。

目前，使用传统机器学习方法预测材料性能已成为关注热点。Jacob 等[4]在化学子结构家族之间使用基于张量积的特征，然后使用了具有成对核的支持向量机（Support Vector Machine,SVM）。Yamanishi 等[5]提出了一种二部图学习方法，将化合物映射到一个共同特征向量空间，并最小化，由已知相互作用链接向量之间的欧几里德距离。Bleakley 等[6]提出了一种二分局部模型，该模型采用化学结构之间的相似性测量，使用了具有已知相互作用的SVM。van Laarhoven 等[7]使用基于网络拓扑的高斯交互配置文件内核，而Gönen[8]使用具有双内核的贝叶斯矩阵分解特征。

传统机器学习方法存在两个不足：第一，需要使用人为设定固定化学特征（即二进制值），这种人为设定的化学特征适用范围小，不能完全体现数据本身特性；第二，没有办法处理简化分子线性输入(SMILES)码，只能将其当作类别型数据进行二进制编码，损失了高分子材料的结构特征。

针对这些问题，本文提出了一种端到端的图神经网络（Graph Neural Network,GNN[9,10]）模型，它可以学习分子图的低维实值向量表示。将SMILES 码转换为图数据表示分子结构，其中顶点是原子，边是化学键。然后将这种图数据按照半径（r）分割为多个子图进行学习和迭代，最终得到分子的向量表示。最后将分子向量、条件、环境等特征，通过构建神经网络进行树脂材料的高温性能预测。在高温树脂数据集实验中，验证了基于GNN 模型可以实现比现有方法更高的模型准确率（准确率能够达到0.6 以上）。而作为对比的基于化学特征的经典机器学习方法，如SVM、梯度提升回归树（GBRT）等方法，准确率难以突破0.3。这表明GNN 模型获得的数据驱动特征比传统人工提取的化学特征更有效。

本工作的意义有以下三个方面：第一，采用GNN 模型可以根据特定任务自学习地提取分子相关化学特征，解决了之前需要人为手动设定化学特征的问题；第二，采用GNN 模型表示高分子材料特征，将高分子的结构表示为由顶点和边构成的图，同时定义顶点的作用半径来模拟高分子化学反应的迭代过程，可以更全面地提取高分子的结构和反应特征；第三，通过和传统机器学习方法在树脂材料数据集上的高温性能预测实验的比较，证实GNN 模型方法相较于传统机器学习模型，预测准确率提升了一倍以上。

1 数据预处理

数据集由1 970 种树脂材料组成，为非公开数据集，研究对象是：在空气、氧气、氮气等环境下，升温速率分别为5、10、20、40 ℃/min 时，树脂材料质量损失5%的最高温度（Td5%）。

1.1 处理数值型数据

本文使用线性函数归一化方法对原始数据执行线性变换，使结果被映射到[0,1]区间，这样会让原始数据等比缩放。归一化操作公式为：

式中：X表示原始数据；Xmin、Xmax分别表示数据最小值、最大值；Xnorm为归一后的结果。

1.2 处理类别型数据

气体和升温幅度这类文字描述数据都属于类别型特征，原始输入是字符串，采用二进制编码方法处理。首先将每个类别特征赋予标签（id）值，然后对这些id 值进行二进制编码。当某个特征存在4 种取值可能性时，这4 个取值可以被表示为001，010，011，100。本质上是利用二进制的方法对id 值进行哈希映射，最终能够得到0 和1 表示的特征向量。例如，使用了氮气，编号为001；使用了空气，编号为010；以此类推。

1.3 处理重复数据

在本数据集中，存在大量环境、条件、升温速率、SMILES 码等信息完全一致，而只有Td5%不同的情况。这是因为树脂材料SMILES 码的链长难以给出所致。这样的数据会对模型产生错误干扰，因此从1 970 种树脂材料的原始数据集中保留了879 种进行模型构建。

2 方法

图1 是本方法的整体流程图。首先利用化学信息学开源工具包（RDKit）库将高分子的SMILES 码转换为图数据，然后通过图神经网络处理，提取高分子对应的结构特征和反应特征，得到分子图的分子向量；最后结合数值、类别等数据，采用全连接神经网络进行回归分析，得到高温性能的预测结果。

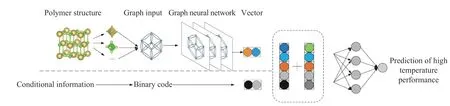
图1 流程图Fig.1 Flow chart

2.1 分子图的GNN

利用GNN 来绘制分子图以获得分子图的低维实值向量表示。GNN 映射图 G到一个向量y∈Rd具有两个函数，即转移函数和输出函数（分别在2.3 节和2.4 节详细说明）。转移函数根据每个顶点的相邻顶点和边更新信息，并通过输出函数将顶点集映射到分子向量。这两个函数都是使用神经网络实现的。其中，转移函数和输出函数都是可微的，函数中的所有参数，包括输入特征，都是通过反向传播学习的。

2.2 输入：嵌入r 半径子图

如图2 所示，本文以乙醛的SMILES 码CC=O 为例，以r=1 和r=2 分为两个子图，即图2 的上下两个部分。然后分别以两个碳原子为中心，寻找r半径的原子，以及它们之间的化学键。即图表示为G=(V,E)，其中V是顶点集合，E是边的集合。在一个分子中，vi∈V是第i个原子，而eij∈E是第i个和第j个原子之间的化学键。最后需要将所有原子和化学键嵌入到d维实值向量空间中。

图2 GNN 得到的分子图以及嵌入r 半径子图Fig.2 GNN for molecular graph and the embeddings based on r-radius subgraphs

本文使用的嵌入r半径子图由顶点半径r内的相邻顶点和边组成。这个r被假定等于从一个顶点开始的跳数。给定一个图G=(V,E)，从第i个顶点到半径r内的所有相邻顶点索引的集合N(i,r)，其中，N(i,0)={i}。我们定义顶点vi的r半径子图的公式如下：

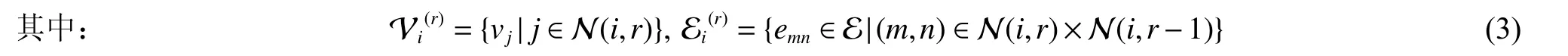
然后，对于每种类型嵌入r半径子图的顶点和r半径子图的边，根据类型分配一个嵌入（即向量），它是随机初始化的，最后在监督学习期间通过反向传播进行训练。图2 显示了r半径子图的顶点、边及其分配的嵌入示例。

2.3 转移函数

2.3.1 顶点转移函数给定一个图 G以及随机初始化的顶点和边嵌入，将时间步进t的第i个顶点嵌入表示为，然后更新，使用下面的转移函数：

其中：σ是逐元素S 型生长曲线（sigmoid）函数σ(x)=1/(1+e−x)，N(i)是i的相邻索引集合，并且是隐藏的邻域向量。可以使用以下神经网络通过考虑相邻顶点和边eij来计算此隐藏向量：

其中f是是非线性激活函数，例如线性整流函数（ReLU）：f(x)=max(0,x)，Wneighbor∈Rd×2d是权重矩阵，bneighbor∈Rd是偏置向量，是时间步进t处第i个和第j个顶点之间的边嵌入。因此，通过对相邻隐藏向量求和，并在时间步进上迭代它们，顶点嵌入可以逐渐在图上收集更多全局信息。

2.3.2 边的转移函数上述迭代过程也可以以类似的方式应用于边的嵌入。在这里，使用两侧顶点嵌入和更新：

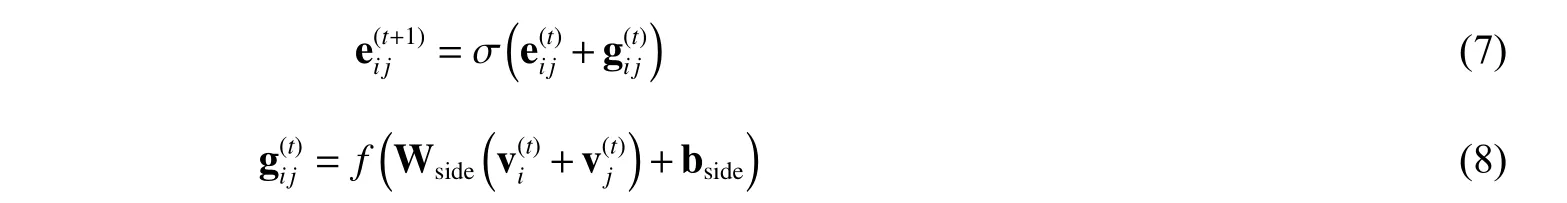
其中：Wside∈Rd×d是权重矩阵；bside∈Rd是偏置向量；因为边在分子图中是无向的，例如C=O 和O=C 是相同的，并且它们的向量也相同，因此，通过顶点和边缘转移函数（示意图见图3）这两个向量嵌入在GNN 模型中被同等考虑并同时更新。

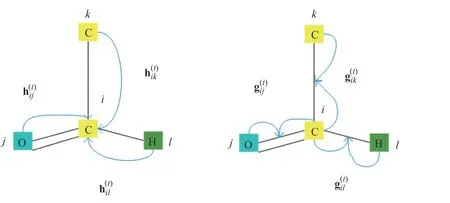
图3 顶点转移函数和边转移函数示意图Fig.3 Schematic diagram of vertex transfer function and edge transfer function

2.4 输出函数：分子向量表示

其中 |V|是分子图中的顶点数。这是获得分子向量的最简单操作。

通过之前的转移函数更新得到的分子向量组合如图4 所示。

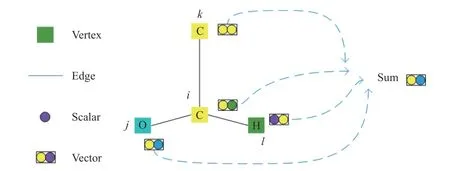
图4 分子向量组合表示Fig.4 Combined representation of numerator vectors

2.5 回归模型

如图1 所示，在得到了分子向量后，将条件、环境、升温速率等信息全部加入到神经网络中，经过几层全连接，通过最后一层sigmoid 函数，得到最终回归模型。神经网络的损失函数设定为均方误差（MSE），最后一层激活函数设定为sigmoid 函数σ(x)=1/(1+e−x)。

式中：f(xi)为预测值；yi为真实值。

3 实验

3.1 训练

数据按照9∶1 的比例划分为训练集和测试集。SMILES 码转换为图数据，并提取分子图的各种信息，例如原子类型、化学键和原子的邻接表。

我们使用Chainer（3.2.0 版[11]）实现GNN，这些神经网络的训练细节如下：优化适应性矩估计（ADAM）[12]，这是基于随机梯度下降（SGD）算法中的一个最常见方法；半径r为0（即每个原子和化学键）、1 或2；窗口大小为11（固定）；顶点、边和n-gram 的向量维数为5、10、20 和30；GNN 中的时间步数（即深度）为2、3、4。注意batch size 为1；一个批次包含一个分子，该分子包含相对较多的顶点和边。此外，当batch size 取1 时，模型收敛可取得最佳效果。使用五折交叉验证，对上述超参数组合进行网格搜索得到最佳参数组合。训练用机器参数为显卡NVIDIA Tesla V100。

图5 展示了训练和验证过程中的Loss 曲线图。其中蓝色、橙色、绿色为训练过程中的Loss 曲线，红色、紫色、棕色为验证过程中的Loss 曲线。横轴为训练迭代次数，纵轴为Loss 值。在经过大概400次训练迭代之后，整个模型已经趋于稳定。采用MSE 和平均绝对误差（MAE）两种方法表达的损失函数之间存在0.05 左右的误差。在训练过程中，MSE 和MAE 损失函数均存在较大波动。

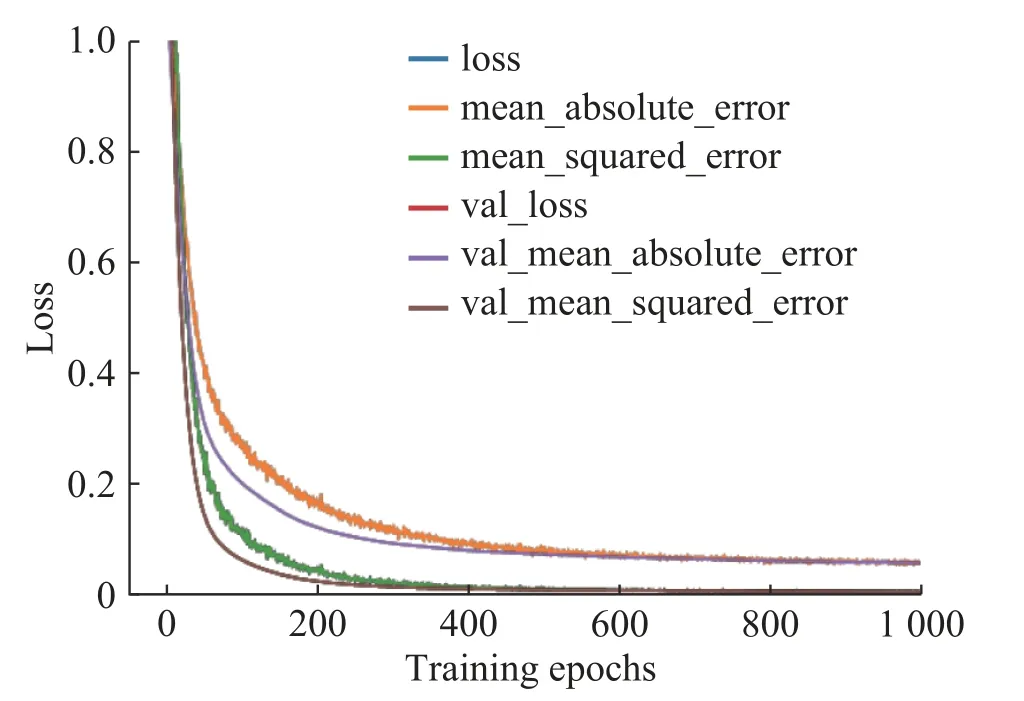
图5 模型训练验证Loss 曲线图Fig.5 Model training and verification loss curves

图5 的Loss 曲线表明GNN 模型能够很好地收敛。曲线的波动下降趋势可能是因为学习率设置过大造成的，但是在训练200 次迭代之后明显波动减少，训练400 次迭代之后，波动几乎消失。因为模型最终走向收敛，所以这种情况下，并未调整学习率。MSE 和MAE 之间的差距是由于其计算公式导致的，任何一个小数的平方，都会更接近于0。

3.2 评价指标

本文采用MAE，均方根误差（RMSE）和决定系数（R2）来对实验结果进行评价，它们的定义分别如下所示：

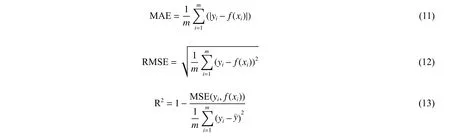
MAE 表示计算每个样本预测值f(xi)与真实值yi之差的绝对值，然后求和取平均值。MAE 用来评估预测结果与真实数据的接近程度，该值越小拟合效果越好。RMSE 表示预测值的离散程度，其值越小拟合效果越好。R2取值在[0，1]区间，越接近于1，表示模型预测能力越好；越接近于0，表示模型预测能力越差；当为负值时，表示模型预测能力非常差。

4 结果与讨论

4.1 结果

在测试集的测试中，选择了SVM[13]、梯度提升回归树（GBRT）[14]、随机森林（RF）[15]这三种传统的机器学习方法作为和GNN 模型相对比的模型。

表1 中，以R2作为回归准确率的评价指标，GNN 模型的准确率能够达到0.68 左右，相较于其他传统机器学习方法均成倍提升。以MAE 和RMSE 的评价标准来看，GNN 模型是所有模型中数值最小的，也是指标最好的，分别能达到23.41 和15.63。

表1 不同模型应用于数据集的指标Table 1 Indicators of different models applied to the data set

图6 显示了预测结果，大部分预测结果比较准确，但是有少许值完全偏离。从图中选择了两个差距很大的，两个差距较小的样本列举在表2 中。

图6 预测结果Fig.6 Prediction Result

4.2 讨论

SVM 模型的均方根误差和平均绝对误差最大，表明SVM 模型训练的精度不如其他模型；GBRT 和RF作为集成学习的样例，准确率确实比SVM 好，但是提升效果不明显。GNN 模型性能非常好，R2的准确率能够达到0.68 左右，RMSE 的准确率约为23，MAE 的准确率小于16，这些指标说明GNN 模型算法明显优于其他方法，其训练精度最高。因此，从表1 模型训练精度来看，无论是均方根误差还是平均绝对误差，GNN 模型的误差都小于SVM、GBRT 和RF 模型误差，从中可以看出在样本量不大的情况下，GNN 模型能够展现出较强的数据拟合能力。另外，从训练时长来看，GNN模型尽管采用并行的显卡辅助计算方法，训练速率会比传统机器学习方法慢很多，这也是神经网络算法的缺点，会大量的占用计算资源和时长。采用训练GNN 模型预测树脂材料的Td5%，不仅能够得到最小的均方误差，而且能够解释60%以上的方差变化，因此GNN 模型算法在避免过拟合的情况下，取得了最佳效果。

在表2 中，*CC(*)C 差值在289 的原因可能是，这是一种只有碳的链式基础结构，而链长未知，所以误差很大。c1ccc(*)c(O)c1 结构可能因为训练数据集中有一个*CO*的真实值为270，所以导致和CO 相关结构的准确率都不高，误差也较大。*C(F)(F)C(*)(F)F 结构可能因为受氟元素的影响更多，误差较小。*Nc1c(C(C)C)cc(*)cc1C(C)C 结构可能因为更受氮元素的影响，而且是非基础结构，误差较小。可能因为越是基础结构，越是影响模型准确性，所以对于基础结构需要更加准确的信息，对于链式结构需要给出明确链长。显然，数据质量在很大程度上决定着模型准确率。

表2 结果分析表Table 2 Result analysis

下一步工作除了继续进行GNN 模型优化之外，还需在数据层面进行更多优化。由于SMILES 码链长难以给出，预测结果还有很大的提升空间，之后如果能够得到更加详实的数据，尽量保证全部数据进入模型训练，将大大提高模型准确率。此外，用于三维结构化的GNN（3D-GNN）模型开发是一项重大挑战。特别是3DGNN 模型能够从结构的角度获得更优的性能，提供更详细的分析，并为化合物之间的相互作用位点获取更多有用信息。