基于检测车数据的JTC补偿电容容值估计方法
2022-01-09王少迪赵林海孟景辉高利民
王少迪,赵林海,孟景辉,吴 楠,高利民
(1.北京交通大学 电子信息工程学院, 北京 100044;2.中国铁道科学研究院集团有限公司 基础设施检测研究所, 北京 100081;3.中国铁道科学研究院集团有限公司 基础设施检测中心, 北京 100081)
无绝缘轨道电路(Jointless Track Circuit, JTC)作为列控系统的重要组成部分,其轨面上所均匀分布的补偿电容在保障信号传输质量方面具有重要作用。当前,补偿电容故障主要有断线和容值下降两种模式[1],其常规检测主要通过定期开行检测车的方式来实现。随着我国铁路的发展,对铁路信号设备的维护已由 “故障修”向“状态修”转变。因此,对于补偿电容,对其仅实现故障诊断已不能满足“状态修”的要求,为此,基于检测车对补偿电容进行估值就具有十分重要的意义。
目前,国内外还没有利用检测车数据实现补偿电容容值估计的研究。关于补偿电容的相近研究,主要集中在利用检测车检测原理分析与机车信号数据实现对补偿电容断线的故障诊断。文献[2]介绍了电务检测车的基本功能,探讨了实现这些功能的技术方法与设备结构。文献[3] 针对检测车补偿电容检测数据提出基于差分分析故障诊断方法。文献[4]使用数理统计方法,利用检测车数据对轨道电路养护维修提供支持。文献[5]提出基于证据融合理论和趋势分析的补偿电容故障检测方法。文献[6]提出基于独立因素分析的补偿电容多故障检测方法。文献[7]提出基于偏最小二乘回归与神经网络的补偿电容故障检测方法。文献[8]提出基于传递置信模型的补偿电容故障诊断算法。
此外,文献[9]提出基于机车信号感应电压幅值包络的补偿电容估值方法。此方法考虑检测车检测范围更广且检测数据可集中处理,更便于实现跨局、跨地区的综合性数据挖掘,进而能得到更为准确的数学模型和估值方法。
本文首先基于有限元和电磁场理论建立检测车补偿电容检测过程的仿真模型,并以此分析相应幅值包络中的脉冲峰值的影响因素及其影响规律,提出补偿电容容值的回归计算方法。实验表明,本文方法对补偿电容估值较为准确,且对于钢轨电感这一主要影响因素有较高的鲁棒性,可为进一步实现补偿电容的“状态修”提供理论支持。
1 检测车补偿电容检测系统的构成与原理
1.1 系统构成
检测车补偿电容检测系统主要设备包括检测主机、发射天线、接收天线和传输电缆等,见图1。
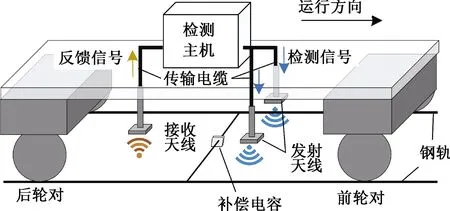
图1 检测车补偿电容检测系统的构成与工作原理
检测主机:产生检测信号,供发射天线向轨面发射并接收来自接收天线的反馈信号。
发射天线:两个,分别安装在检测车底部两根铁轨的上方,用于向轨道线路发射检测信号。
接收天线:一个,安装在车底两条钢轨中线处的上方,用于接收来自轨面线路的反馈信号。
传输电缆:将检测主机分别与发射天线和接收天线相连接,构成相应的信号传输通路。
1.2 工作原理
检测车对补偿电容的检测基于电磁感应原理,按照信号的传递方向可分为发送和接收两个环节。
发送环节是指在检测车运行过程中,检测主机所产生的特定频率的检测信号,经相应传输电缆传输到两个发射天线,并由发射天线不间断地向钢轨线路发射。
对于接收环节,由于钢轨线路与发射、接收天线附近的前、后列车轮对共同构成一个闭合回路,故由麦克斯韦-安培定理[10]可知,该闭合回路会产生一个由发射天线发射信号所引起的交变磁场,而由法拉第电磁感应定理[10]可知,上述交变磁场会在该闭合回路中产生相应的感生电动势,进而形成相应的感生电流。同理,由麦克斯韦-安培定理[10]和法拉第电磁感应定理[10]可知,该闭合回路中的感生电流又会通过电磁感应,在车载接收天线中产生相应的感应电压,即反馈信号。
随着列车的运行,当闭合回路中含有补偿电容时,由于电容C与电感L的阻抗作用相反,会使回路总阻抗逐渐减小,相应的感应电流逐渐增大;当检测车运行到某特定位置时,回路的总感抗将与补偿电容的容抗近似相等,闭合回路中的感应电流达到最大;随着检测车的继续运行,补偿电容逐步接近后轮对,直至离开闭合回路,回路的总阻抗逐渐增大,相应的感应电流逐渐减小。
由以上分析可知,补偿电容通过中和回路中的感抗,而使回路中的感应电流出现一个由小到大再由大到小的变化过程,且该变化可最终体现在反馈信号幅值包络的变化上。若补偿电容发生故障,则会降低补偿电容对闭合回路感抗的抵消作用,导致反馈信号中该电容所对应幅值包络峰值的降低,检测车凭借此变化实现对补偿电容的故障检测。
2 基于有限元的检测车补偿电容检测过程的建模与验证
2.1 模型建立
利用有限元方法对上述检测过程的发送和接收环节进行整体建模,见图2。
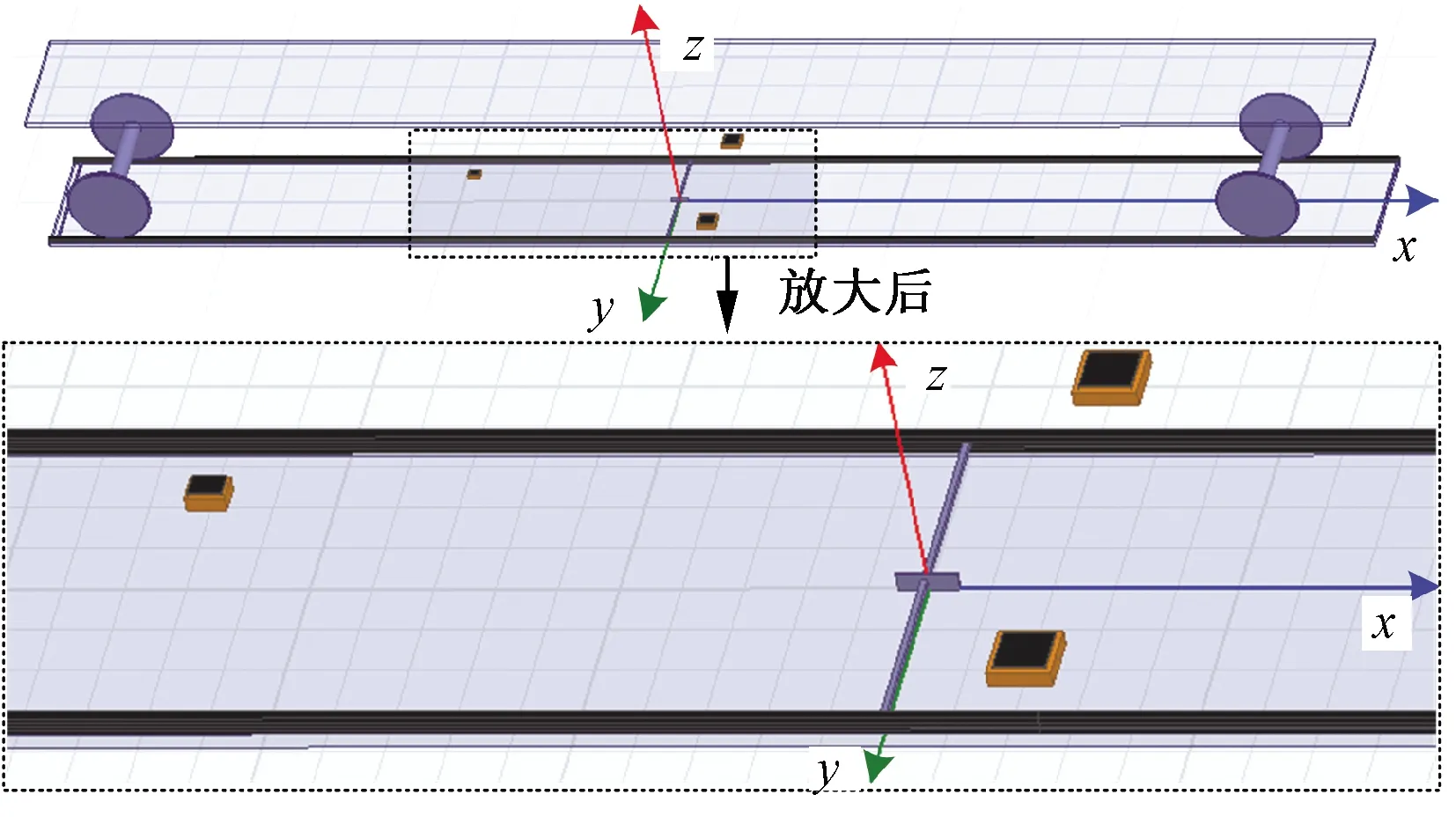
图2 检测车补偿电容检测过程的有限元模型
图2中,基于检测车和轨道线路的系统结构,分别建立了道床、钢轨、前后轮对、补偿电容以及检测车的发射天线和接收天线的3D模型。以补偿电容所在位置为坐标原点,建立三维坐标系。其中,x方向为检测车运行方向,y方向为垂直钢轨向下方向,z方向为垂直轨道向上方向。
基于麦克斯韦方程,分别对钢轨、天线、道床和补偿电容等有电流区域和空气等无电流区域,利用边界条件求解每个子域,再通过变分方法将各个子域的结果进行整合而获得整个区域的解。即有
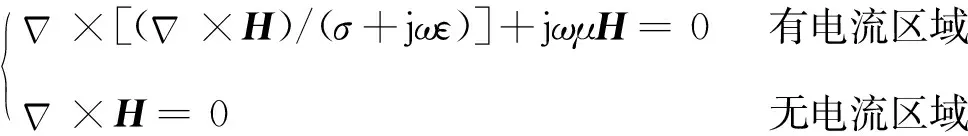
( 1 )

质的介电常数;μ为介质的磁导率;H为磁场强度;ω为发送信号角频率,其信号可表示
I(t)=Im·sin(2πft+φ)
( 2 )
式中:f、Im和φ分别为I(t)的频率、振幅和初始相位。
设检测车前、后轮对间距为Lc,补偿电容与检测车前轮对间距为xc,则基于图2所建模型,可得接收天线中感应电动势Er(xc,t)为
Er(xc,t)=Er(xc)sin(2πft+φt),xc∈[0,Lc]
( 3 )
式中:Er(xc)和φt分别为Er(xc,t)的振幅和相位。
进一步,本文基于图2所建模型,以步长Δx=1 m为间隔,以xc=0为起点,以xc=Lc为终点,建立不同xc取值下相应的有限元模型,并基于式(3)提取其中的Er(xc)振幅参数,按图3所示,构建反馈信号的幅值包络序列Er,即有

图3 反馈信号幅值包络序列Er的建模求解流程图
Er={Er(xc)|xc=0,1,2,…,Lc}
( 4 )
2.2 模型验证
目前国内有ZPW-2000A与ZPW-2000R两种型号的JTC,其补偿电容容值并不相同。其中,高速铁路ZPW-2000A型轨道电路中的补偿电容为25 μF,既有线ZPW-2000A型轨道电路有40、46、50、55 μF四种容值电容[11],而ZPW-2000R型轨道电路中也存在28、30、33、40 μF四种容值电容[12]。故针对这两种电路,分别选取了标准容值为50、28μF的补偿电容检测数据,再基于相同条件,设置模型[13-16]并根据图3所示流程得到相应仿真结果,见图4。
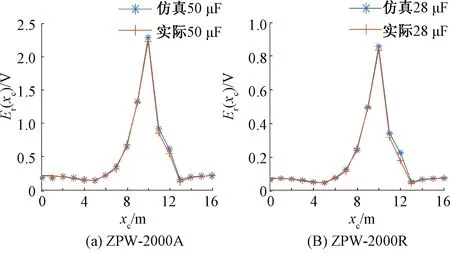
图4 ZPW-2000A与ZPW-2000R型轨道电路50、28 μF补偿电容所对应的Er(xc,t)实际数据与仿真数据的对比
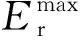
3 补偿电容检测过程的影响因素分析
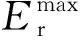
同时,为便于衡量各影响因素的影响程度,定义影响度ρ指标,即有
( 5 )
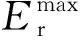
3.1 补偿电容容值对的影响分析
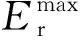
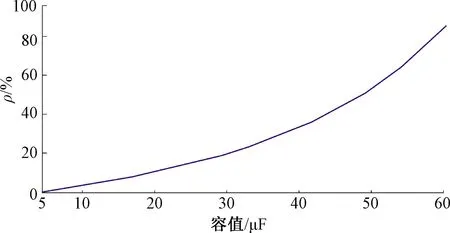
图5 补偿电容容值对的影响度ρ
3.2 钢轨电感对的影响分析
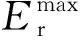
图6 钢轨电感对的影响度ρ
3.3 钢轨电阻对的影响分析
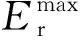
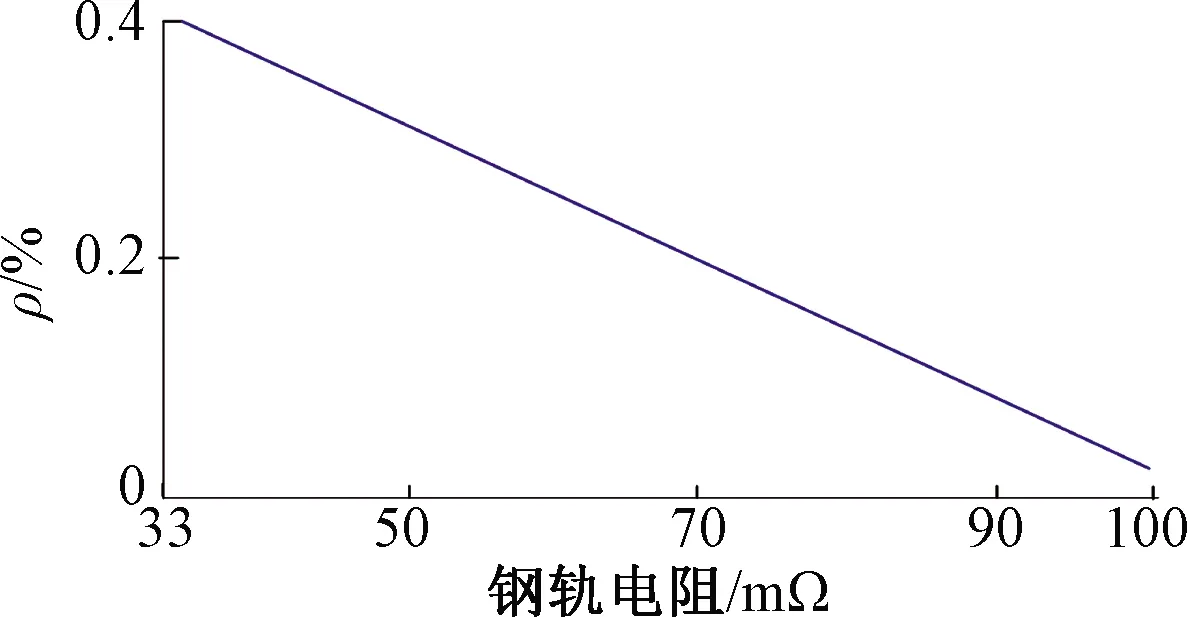
图7 钢轨电阻对的影响度ρ
3.4 道床电阻对的影响分析

图8 道床电阻对的影响度ρ
4 补偿电容容值估计算法设计

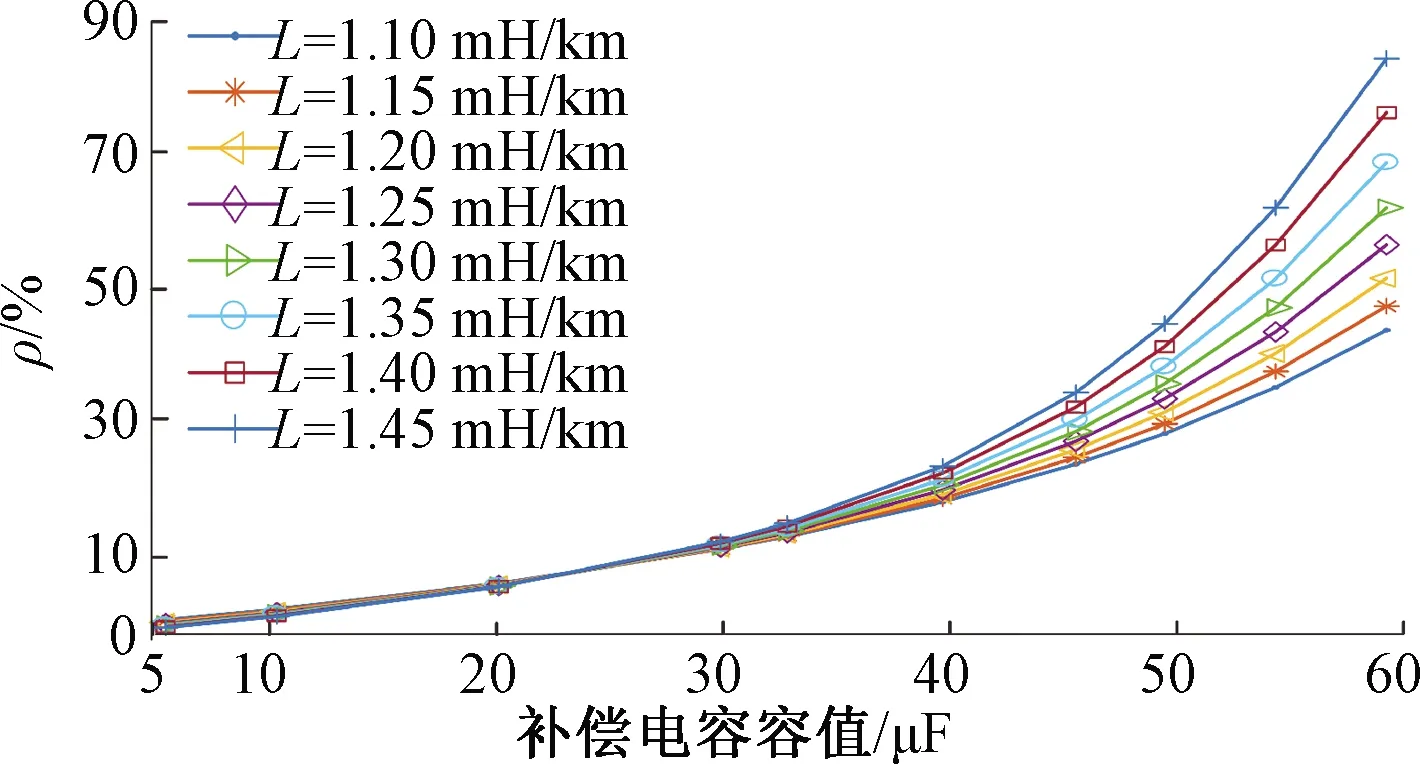
图9 补偿电容容值、钢轨感抗对的影响度ρ
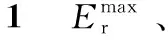
表补偿电容容值C和钢轨电感L的拟合结果和拟合优度
由表1可知,指数函数拟合结果最优,即有
( 6 )
可见,基于公式(6)在已知钢轨电感和幅值包络峰值的条件下,可实现对补偿电容容值的估计。
4.2 算法设计
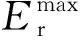
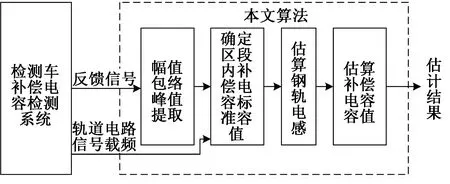
图10 基于检测车数数据的补偿电容容值估计算法
(1)幅值包络峰值提取
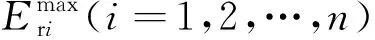
( 7 )
(2)确定区段内补偿电容标准值
由文献[11]可知,根据检测车所提取的该JTC所对应的机车信号载频频率,可确定该区段各补偿电容的标准值Cs。
(3)估算钢轨电感
( 8 )
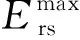
( 9 )
(4)估算补偿电容容值Cgi
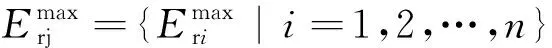
(10)
5 实验验证
5.1 基于实际数据的算法功能验证
考虑到补偿电容断线是其容值下降的一个特例,补偿电容断线,其容值为0,检测车可直接判出,不用估值,故本文选取容值下降情况进行验证。图11为检测车在某轨道电路上运行时所获得的补偿电容检测数据,检测车判断补偿电容C11故障,后经人工实地勘测,确认C11电容容值已降为40.2 μF,而其余补偿电容容值均在正常范围内。
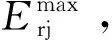
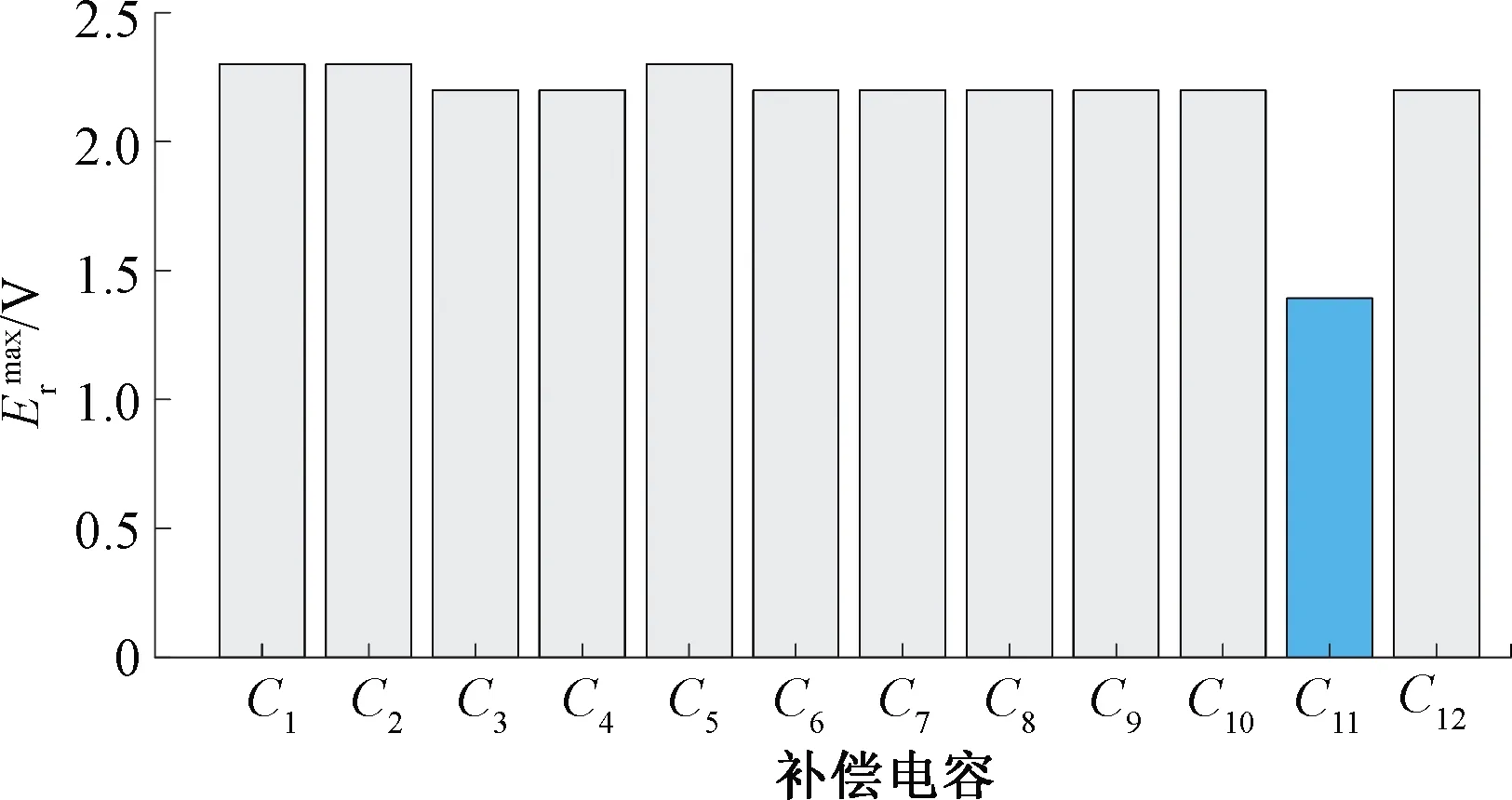
图12 图11中12个补偿电容所对应幅值包络的峰值集
然后,根据检测车机车信号的载频信息为2 000 Hz,确认本区段补偿电容的标准容值Cs=50 μF。
进一步,根据公式(9),计算得到该区段钢轨电感的估计值为Lg=1.34 mH/km。
最后,由公式(10)计算区段内各补偿电容的估计值Cgi(i=1,2,…,n),结果见图13。
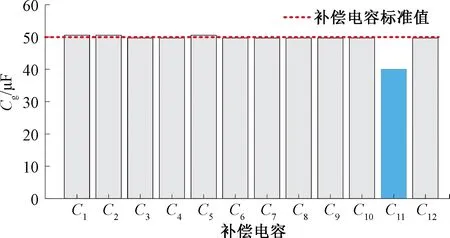
图13 本文算法对图11各补偿电容容值的估计结果
其中,对C11的估计容值为40.18 μF,即绝对误差仅为0.02 μF。可见,本文方法可较为准确地估计补偿电容的容值,对于故障与正常电容的容值均可准确估计,证明了本文所述方法可用来进行补偿电容容值的估计。
5.2 算法性能验证
为验证算法性能,选取检测车所检测的60个区段共836个补偿电容所对应的峰值包络数据构造测试集。其中,每个区段均包含一个故障电容,同时考虑完备性,数据中包含有高速铁路和既有线不同JTC所对应的多种容值的补偿电容数据。
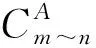
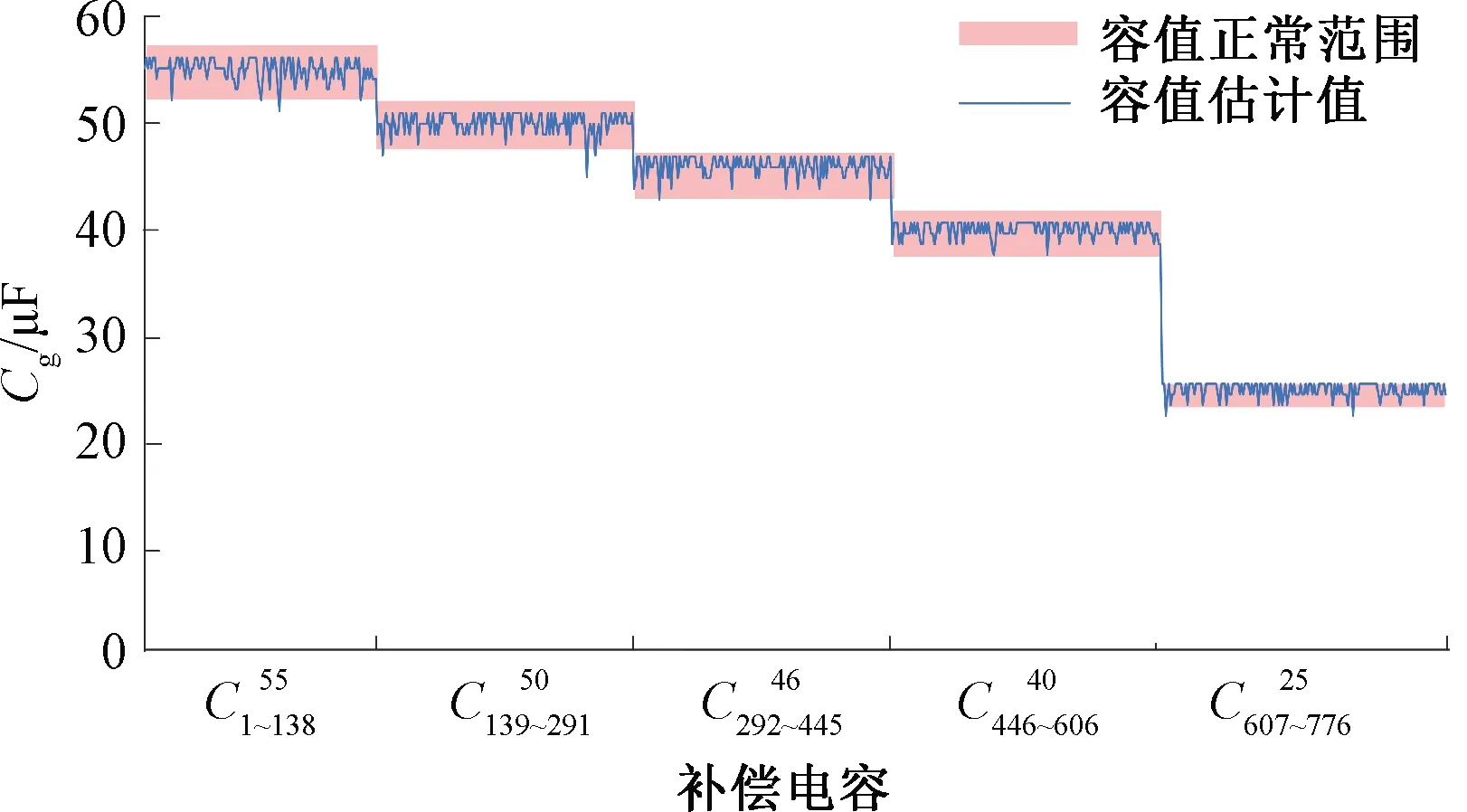
图14 本文算法对测试集内正常电容容值的估计结果
由图14可知,对于正常电容的估计,估计结果有98%落在正常范围内。
对于测试集中的60个故障电容,由于维护人员会在更换过程中进行测量并记录容值,因此可以得到其实测值。故本文将对故障电容的估计值与实测值相比较,其绝对误差见图15。
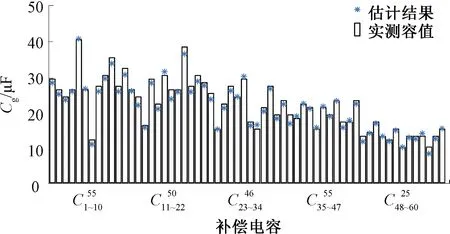
图15 本文算法对测试集内故障电容容值的估计结果
由图15可知,本文对故障电容容值的估计误差最大为2.6 μF,最小为0。误差原因主要是检测车检测后到工人实地检修这段时间内容值继续下降,以及对一个区段使用同一电感估计值代替各个补偿电容附近钢轨电感,当局部钢轨电感波动较大导致的。通过对图15所示估计结果进行统计,误差值在[0,0.65]μF区间的占总样本数的67%,在(0.65,1.3]μF区间的占总样本数的20%,在(1.3,1.95]μF区间的占总样本数的10%,在(1.95,2.6]μF区间的占总样本数的3%,可见本文算法误差普遍较小。
由上述实验可知,本文所述补偿电容容值估计算法可实现对补偿电容容值较为准确的估计,且不易受钢轨电感、钢轨电阻、道床电阻等因素影响。
6 结论
为满足铁路现场对无绝缘轨道电路补偿电容进行“状态修”的需要,本文基于电磁场理论建立并验证了检测车补偿电容检测过程的有限元模型。在此基础上,分析了补偿电容、钢轨阻抗和道床电阻对检测车接收天线中反馈信号幅值包络的影响程度,建立了补偿电容、钢轨电感和反馈信号幅值包络峰值三者间的回归模型。根据检测车对补偿电容的故障诊断特点,提出了基于检测车数据的钢轨电感回归估计方法,并以此给出了补偿电容容值的估算公式。实验表明,本文方法具有对补偿电容容值估计准确、鲁棒性强等特点,并为进一步实现补偿电容的故障预测和“状态修”提供理论支持。
