高速铁路轮轨耦合振动模态特征及其影响因素研究
2022-01-09马超智曾钦娥崔日新
马超智,高 亮,曾钦娥,崔日新
(1.北京交通大学 土木建筑工程学院, 北京 100044;2.北京市轨道交通建设管理有限公司, 北京 100068)
目前,我国高速铁路已经由大规模建造时期进入长期安全运营保障阶段。伴随着高速铁路大范围服役,轮轨周期性磨耗(车轮多边形、钢轨波磨)、关键部件的疲劳失效等问题逐渐涌现,给列车的运营安全带来了重大隐患[1]。轮轨系统共振导致轮轨动态相互作用在特定频带的加剧,与轮轨周期性磨耗、部件疲劳失效等上述问题的发生密切相关[2-6],亦直接影响着沿线环境的振动噪声特性[7]。因此,明确轮轨系统共振特征,阐明其共振成因,对轮轨周期性磨耗机理的揭示、系统动力响应的评估及控制具有重要意义。
当车辆在轨道上运行时,刚性较大的车轮与柔性较强的钢轨构成了一个刚柔耦合、相互约束的轮轨系统。车轮对钢轨的耦合约束作用会显著改变钢轨的振动行为,例如考虑单车轮作用时钢轨一阶弯曲共振会转变成P2共振,共振频率大幅降低[8];多车轮作用较单车轮作用下钢轨导纳显现出了更多的共振峰[9-10]。因此,仅关注钢轨自身模态特征对轮轨系统共振成因仍无法合理阐明,应进一步将车轮的影响考虑在内,对轮轨耦合系统的模态进行识别。
轮轨耦合系统的模态参数可称之为轮轨耦合振动模态,其求解在模型上可转化为车轮质点与钢轨梁耦合系统的特征值问题。既有虽对单车轮作用下的P2共振模态的频率特征有一定研究[8,11],多数是关注钢轨自身的自由模态或仅是扣件作用下的约束模态[12-14],缺少对多车轮作用下轮轨耦合振动模态的识别,亦不清楚轮轨耦合振动模态的变化对轮轨系统共振的影响规律。
本文旨在识别高速铁路轮轨耦合振动模态,明确其对轮轨系统共振的影响。为此,建立车辆-无砟轨道系统动力学模型,研究随机不平顺激扰下轮轨动力响应在宽频域上的分布特征,通过对比分析单/双轮对作用下轮轨动力响应,明确导致轮轨系统共振的轮轨耦合振动模态,并分析扣件间距、扣件刚度及轴距等因素对轮轨耦合共振响应的影响规律。
1 车辆-无砟轨道系统动力学模型
车辆选用CRH380A型车,无砟轨道选用CRTSⅢ型板式无砟轨道,在建模时同时考虑了下部基础简支梁桥参振的影响(简化为梁模型)。基于文献[15]的车辆-轨道耦合动力学理论,建立车辆-无砟轨道系统动力学模型,见图1,详细建模参数见表1。该系统模型由车辆子系统、钢轨子系统以及无砟道床-桥梁子系统组成[16]。车辆与钢轨之间基于轮轨动态接触模型求解,其中轮轨法向接触采用基于虚拟穿透理论的非Hertz接触算法进行求解[17],切向接触基于Fastsim算法进行求解[18]。由于高铁扣件结构由上下两层具有不同弹性的橡胶垫板和弹性垫板间夹着具有一定质量的铁垫板组成,在中高频范围内该铁垫板将参与振动。为准确表征高铁扣件的动力学行为,钢轨与无砟道床-桥梁子系统间的相互作用采用考虑铁垫板振动的改进扣件模型,即Kelvin-质点-Kelvin串联模型模拟;桥梁支座的模拟采用线性弹簧-阻尼单元。

图1 车辆-无砟轨道系统动力学模型
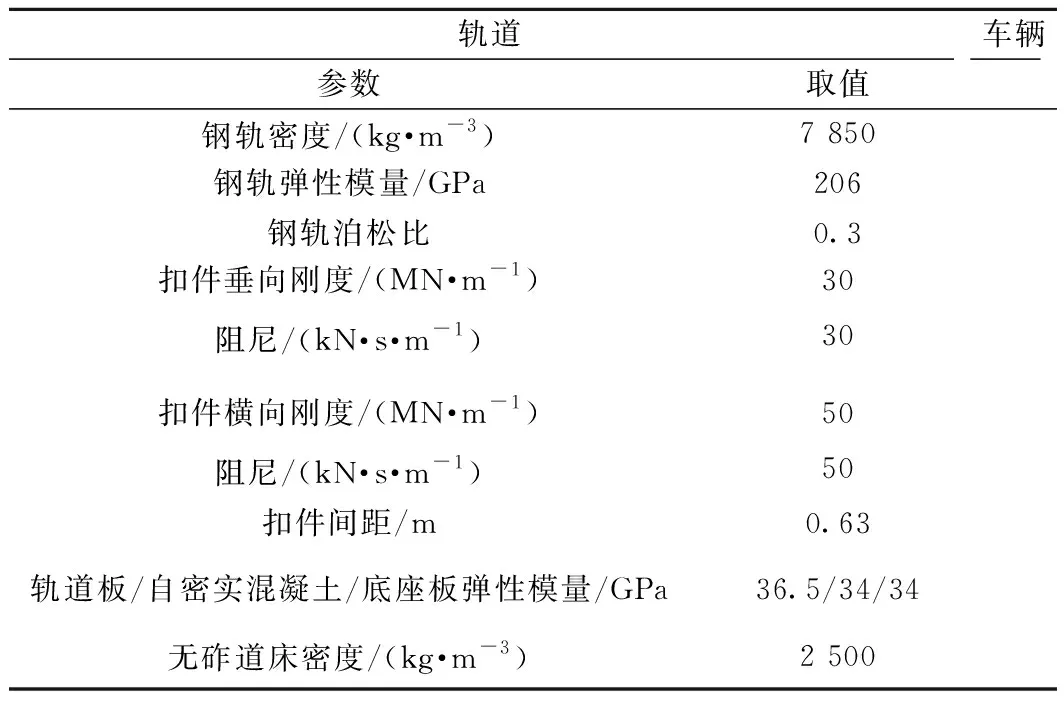
表1 车辆-无砟轨道系统关键参数取值
1.1 车辆-无砟轨道系统模型
车辆为车体、构架和轮对组成的多刚体系统,各刚体之间的相互作用采用线性或非线性的弹簧-阻尼力元模拟。车辆的动力学方程可表示为
(1)
式中:Mv、Dv和Kv分别为车辆系统的质量、阻尼和刚度矩阵;uv为车辆系统各部件的位移矢量;Fwr为轮轨接触力矢量。
钢轨采用Timoshenko梁来模拟其垂、横向弯曲及扭转运动,横向弯曲和扭转运动的方程详细可参见文献[19]。钢轨垂向弯曲的动力学方程为
(2)
(3)
式中:urz、θry分别为钢轨垂向位移、绕y轴转角位移;Er、Gr、Ar、Iry、ρr、κrz分别为钢轨的弹性模量、剪切模量、截面面积、惯性矩、密度及剪切因子;Frfzi(t)、Fwrzj(t)分别为钢轨所受的扣件垂向支反力和轮轨垂向荷载;xfi、xwj分别为扣件支点、轮载的位置;Nf、Nw分别为扣件支点数、轮载个数;δ(·)为狄拉克函数。
无砟道床-桥梁(轨下柔性基础)的动力学响应采用模态叠加法求解,并通过建立有限元模型获取其模态信息。在建立无砟道床-桥梁有限元模型中,无砟道床采用实体单元模拟,考虑其由轨道板、自密实混凝土、底座板的多层结构组成,32 m简支箱梁采用反映其真实截面特性的空间梁单元模拟,无砟道床底座板实体单元的底面节点和梁单元相应节点间通过约束方程进行自由度耦合。为较准确模拟箱梁在空间上的受力特征,将梁放置在箱梁的中性轴处,在箱梁支座位置建立无质量质点单元并与梁采用约束方程进行自由度耦合。桥梁支座处的两个无质量质点施加接地弹簧-阻尼单元以此模拟桥梁支座的弹性支撑作用。此外为防止失稳,约束了梁绕其自身轴的旋转自由度。无砟道床-桥梁子系统的控制方程及响应求解方程为
(4)
(5)

1.2 轮轨界面激扰
轮轨界面激扰造成车辆-轨道系统振动及轮轨磨耗,为激发高频范围内的动态响应,轮轨界面激扰由高速铁路实测轨道随机不平顺叠加短波不平顺组成,不平顺波长范围为0.03~120 m,其中短波不平顺采用在高频随机振动研究领域应用较为广泛的Sato联合粗糙度谱[20]。轮轨界面激扰见图2。
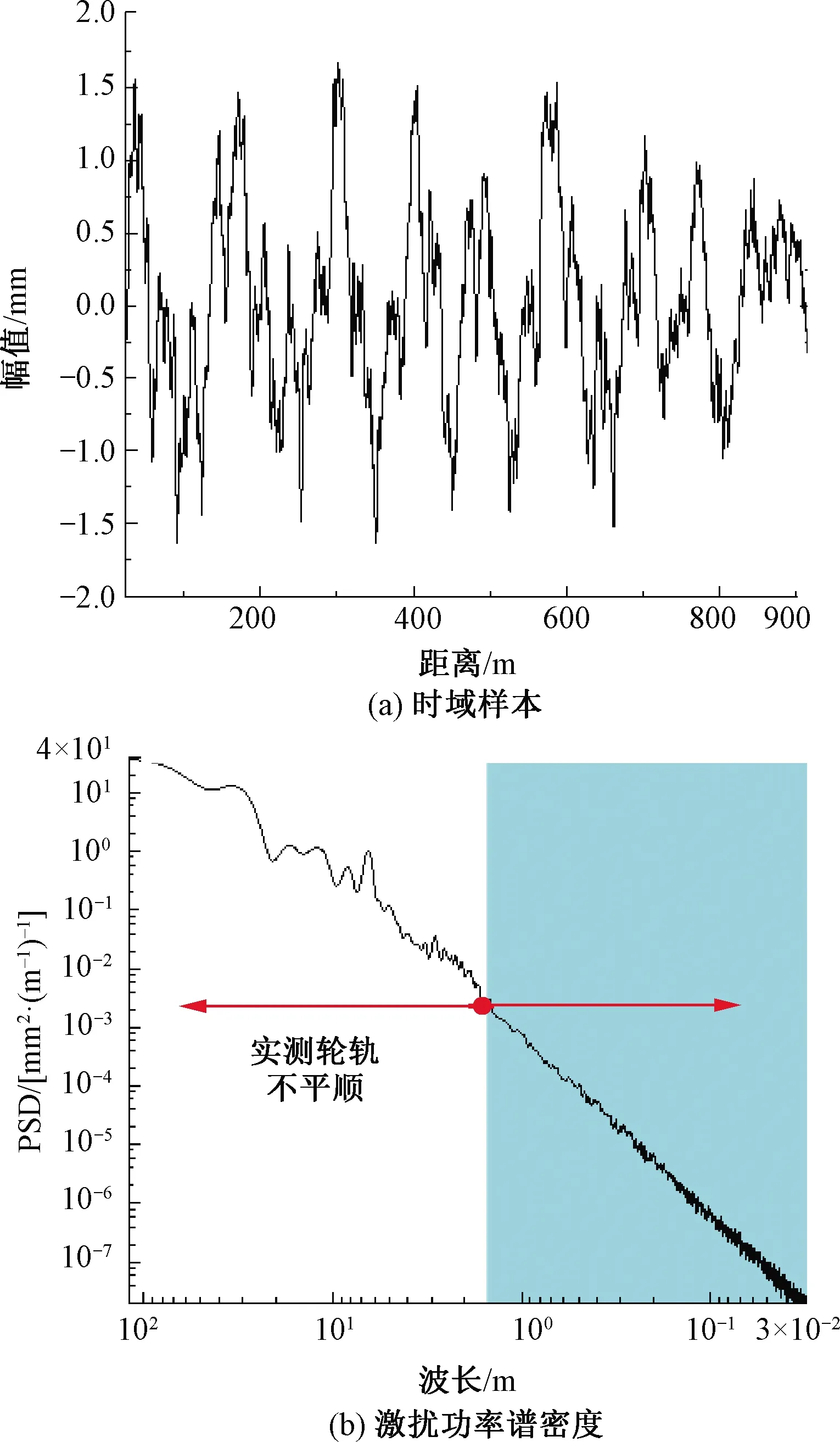
图2 轮轨界面激扰
2 轮轨耦合振动模态研究
2.1 轮轨动力响应分布规律及共振现象
摩擦功率Mwear是反映轮轨间切向动力学响应及黏-滑振动特征的重要指标,其计算公式为
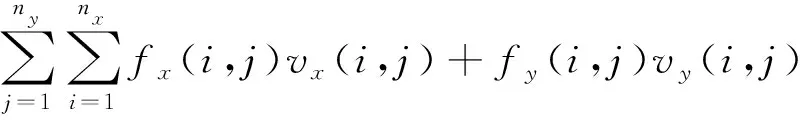
(6)
式中:f为蠕滑力;v为轮轨相对滑动速度;As为接触斑面积;fx(i,j)和fy(i,j)分别为单元格(i,j)的纵横向蠕滑力;vx(i,j)和vy(i,j)分别为单元格(i,j)的轮轨纵横向相对滑动速度;nx和ny为纵横向接触斑网格密度。
摩擦功率在某一频段的共振将导致磨耗在该频段的剧烈波动,进而激化相应波长的不均匀磨耗,最终诱导钢轨波磨、车轮多边形等周期磨耗的萌生[21-23]。因此,摩擦功率共振对诱导轮轨周期性磨耗的萌生具有重要影响。轮轨垂向力可有效反映轮轨间垂向动力学响应特征,对列车运行安全性及沿线环境振动具有重要影响。本文基于这两个指标对轮轨切向及垂向动力响应进行分析,进而明确轮轨动力响应分布规律及共振特征。基于1.1节建立的车辆-无砟轨道系统动力学模型,求解得到不同行车速度下轮轨动力响应特征,见图 3,其中fRP-1、fRP-2、fRP-3、fRP-4为第1、2、3、4共振带,fsp、2fsp分别为扣件通过频率及其2倍频。
由图3可知,1 500 Hz范围内轮轨摩擦功率在40~50 Hz、350~400 Hz、550~650 Hz、950~1 250 Hz存在4个显著共振频带;轮轨垂向力在40~50 Hz、350~400 Hz、550~650 Hz、900~1 200 Hz亦存在4个显著共振频带。摩擦功率和垂向力的共振频带分布相似,其中第1共振属于中低频范畴,其共振响应在全频段范围内最为显著;其余3个共振属于高频范畴,且在550~650 Hz处的共振响应更为突出。此外,不同行车速度下摩擦功率及垂向力的共振频带均不会发生移动,仅是共振峰值发生了变化,表明这4个共振频带的形成主要由车辆-无砟轨道系统的固有振动模态决定。另外,由于扣件周期性离散支撑作用,在扣件通过频率及其倍频处出现了较为显著的尖峰。
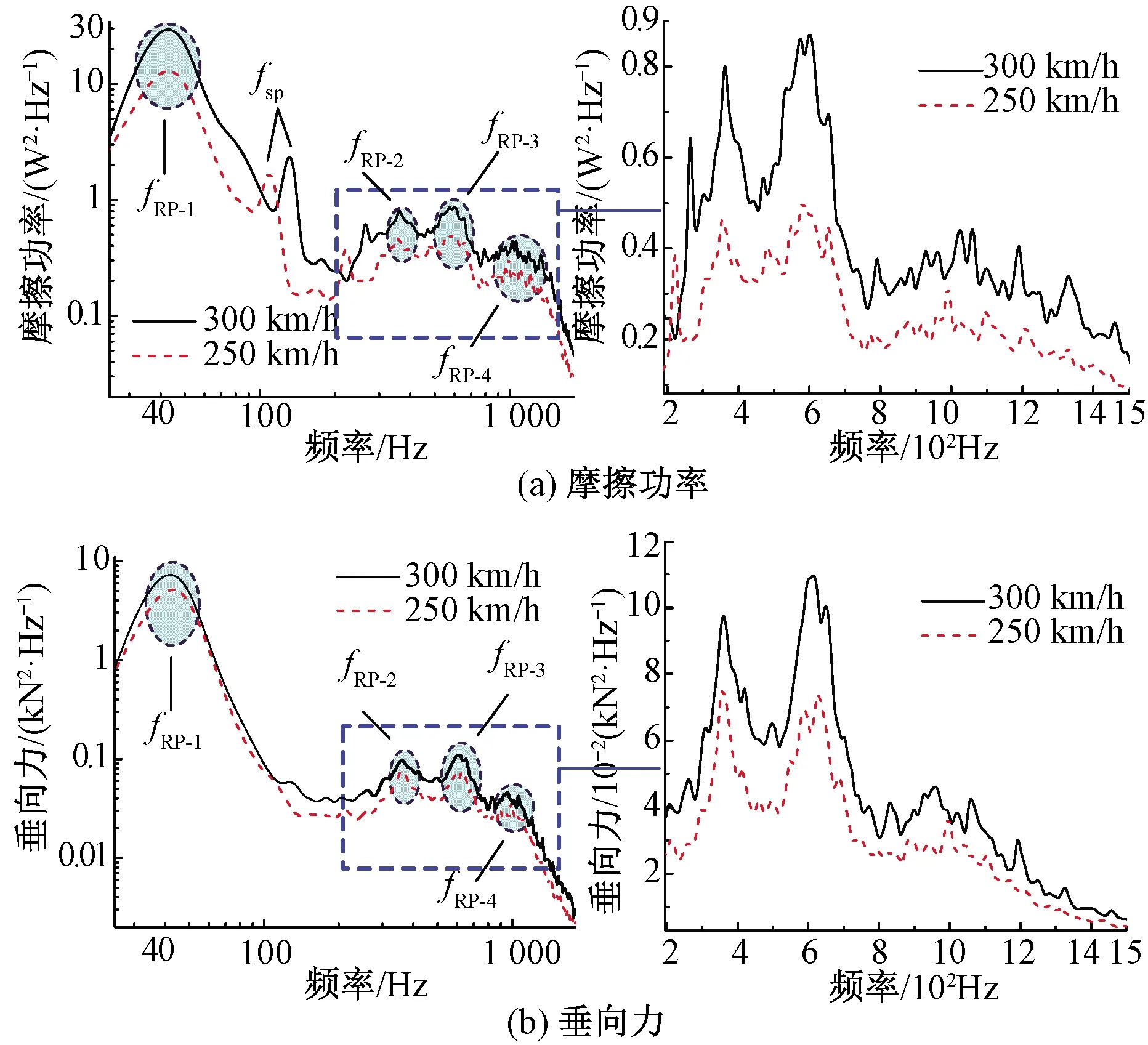
图3 不同行车速度下轮轨动力响应特征
2.2 轮轨系统共振成因及耦合振动模态识别
为揭示轮轨系统共振成因,确定导致轮轨系统摩擦功率及垂向力共振的固有振动模态,建立单轮对/双轮对-钢轨耦合动力学模型,见图4。对于每个轮对,考虑转臂定位和一系悬挂的横向和摇头约束作用,并将其简化为与全局坐标系相连、和实际力学参数一致的线性弹簧-阻尼力元来模拟。由车体和构架传递给轮对的垂向静荷载等效施加在轮对端部轴箱位置处,并考虑与整车模型相同牵引力矩的作用。
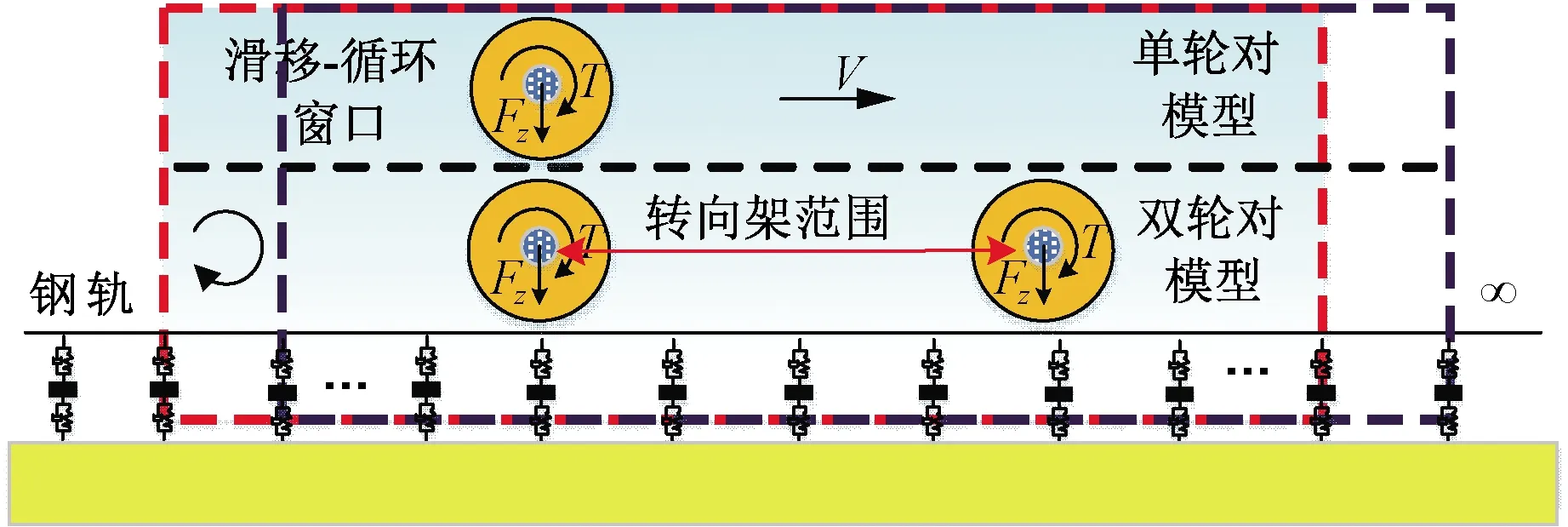
图4 单轮对/双轮对-钢轨耦合动力学模型
仿真得到单-双轮对作用下摩擦功率和垂向力,并和整车模型仿真结果进行对比,见图5、图6。
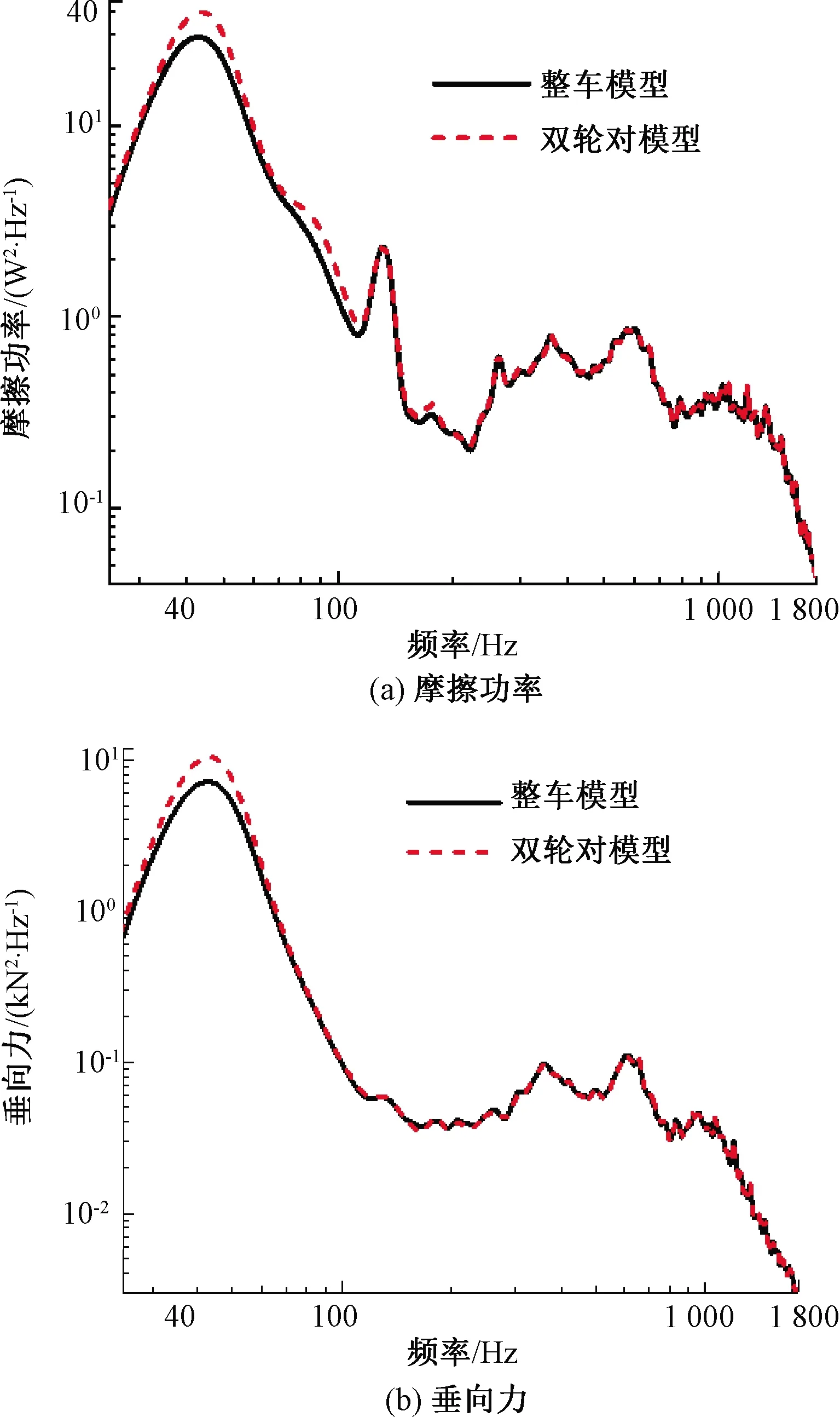
图5 整车/双轮对模型下轮轨动力响应
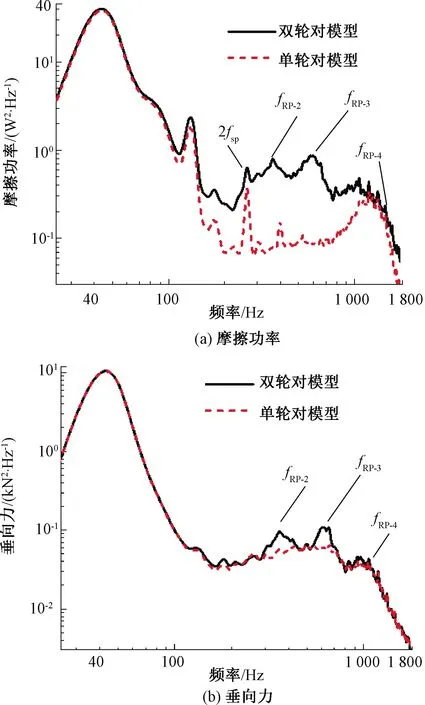
图6 双轮对/单轮对模型下轮轨动力响应
由图5可知,相比双轮对模型,整车模型由于车辆上部结构的刚体运动及无砟道床-桥梁柔性振动的阻尼耗能作用,降低了其第1共振的响应峰值,但对200 Hz以上的高频动态响应影响较小。此外,双轮对模型与整车模型仿真得到的轮轨动力响应共振频带分布相吻合,表明车辆上部结构及无砟道床-桥梁柔性体的振动不是造成轮轨系统显著共振的根本成因。由图6可知,单轮对模型较双轮对模型仿真得到的中低频动力响应无变化而高频动力响应特征差异明显:其第2、3共振带消失,第4共振响应峰值减小,表明轮轨系统的第2、3、4共振带的形成与转向架车轮间钢轨局部振动模态相关。值得注意的是,单轮对模型垂向力550 Hz处较为显著共振峰是由轮轨P1共振诱发的。
进一步建立转向架范围内双车轮-钢轨耦合振动模态分析模型,见图7。该模型中钢轨简化为梁模型并被考虑铁垫板振动的改进扣件模型周期离散支撑,车轮简化为仅保留其惯性属性的质点,车轮与钢轨间的约束简化为线性化Hertz弹簧,其刚度为
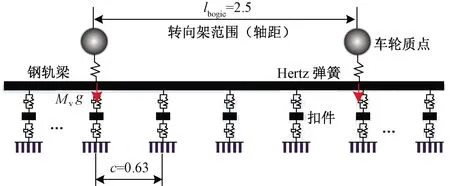
图7 轮轨耦合振动模态分析模型(单位:m)
1.5×(3.86×0.43-0.115×10-8)-3/2×
(6.7×10-5)1/2≈1.4×109N/m
(7)
式中:G为轮轨接触常数;δ为静轮载下轮轨压缩量。
以静轮载下钢轨变形为初始条件,求解得到轮轨耦合振动模态特征见图8。

图8 轮轨耦合振动模态
轮轨耦合振动模态共有4种模式:P2共振模态以及转向架车轮间钢轨2阶弯曲、3阶弯曲和4阶弯曲模态,其模态频率分别与轮轨动力响应的4个共振频带相匹配,可以推断这4种模式的轮轨耦合振动模态是诱发轮轨系统共振的根本原因。进一步说明:①P2共振模态为单车轮与钢轨的等幅同相振动模态,与轮对个数无关,在单轮对模型和双轮对模型中该模态均存在,因此在单-双轮对模型的轮轨动力响应中存在相一致的第1共振。②对于转向架车轮间钢轨2阶弯曲、3阶弯曲模态,其在单轮对模型中不存在,这是单轮轨相互作用下摩擦功率和垂向力无第2、3共振带的内在原因。③对于转向架车轮间钢轨4阶弯曲模态,由于转向架轴距约为扣件间距的4倍,其模态振型半波长基本等于扣件间距,此时钢轨振型像被钉在扣件节点上,实质为钢轨pinned-pinned振动模态。但该模态与传统单轮轨作用下钢轨pinned-pinned振动模态不同的是轮轨接触点不在钢轨弯曲振型的波节位置,且前后轮轨接触点的振动相位相反,这是造成单-双轮轨作用下第4共振响应存在差异的原因。转向架车轮间钢轨pinned-pinned振动模态是转向架双轮间波传递及反射、扣件离散支撑共同作用的结果,其不仅与扣件离散支撑间距有关,还与转向架轴距有关。
对轮轨耦合振动模态特征进一步分析发现,P2共振模态特征的出现是由于车轮位于钢轨弯曲振型的波腹处,造成车轮与钢轨明显的等幅同相振动,且影响范围广(约8个扣件间距)、模态频率低,这容易造成振动能量分别向车辆上部结构、轨下基础传递并耗散,使得考虑车辆上部结构及轨下基础的振动后P2共振响应峰值相比不考虑时有所降低。转向架车轮间钢轨2阶弯曲、3阶弯曲及pinned-pinned振动模态为钢轨局部弯曲振动模态,车轮位于或接近钢轨弯曲振型的波节处,且模态频率高,主要造成振动能量沿钢轨纵向在车轮间传递及反射,容易激化轮轨表面的短波磨耗。综上,轮轨耦合振动模态可归为两类:一类是单车轮和钢轨作等幅同相振动的P2共振模态;另一类是转向架范围内双车轮约束下钢轨的局部弯曲振动模态。
2.3 轮轨耦合振动模态对轮轨周期磨耗影响
对高速铁路现场出现的钢轨波磨及车轮多边形病害调研结果可知,钢轨波磨的波长多为125~160 mm和65~80 mm(列车速度300 km/h),此时对应的波磨通过频率为521~667 Hz和1 040~1 282 Hz[24];车轮多边形的阶数为22~24阶(列车速度250 km/h),对应的激扰频率约为590 Hz。钢轨波磨和车轮多边形的激扰频率与转向架车轮间钢轨3阶弯曲、pinned-pinned振动模态频率相吻合,推断这两种模态对车轮多边形、钢轨波磨的形成具有重要影响。
进一步分析轮轨耦合振动模态对轮轨周期磨耗的影响,可基于多边形增长率[25]、波磨增长率[26]作简要讨论。多边形或波磨增长率的数值衡量着某一频带粗糙度的增长或削弱情况,增长率为正表现为粗糙度增长而负值表现为削弱。不同轮对作用下轮轨周期磨耗形成特征见图9。由图9可知,单轮对模型较双轮对模型仿真得到的多边形和波磨特征差异显著,且基于双轮对模型获得的结果与高铁现场调研结果相吻合,表明车轮多边形、钢轨波磨等轮轨周期磨耗的形成与转向架车轮间钢轨局部弯曲共振密切相关。综合单-双轮轨作用下轮轨动力响应对比结果可以推断转向架车轮间钢轨3阶弯曲及pinned-pinned共振对轮轨周期性磨耗形成具有重要贡献。

图9 不同轮对作用下轮轨周期磨耗形成特征
需要指出的是,基于传统Kelvin扣件模型仿真得到的转向架车轮间钢轨3阶弯曲模态频率约为650 Hz[25],这个频率与现场发生的多边形激扰频率(590 Hz)存在约2阶的差异(一阶频率等于车轮旋转频率f=V/(2πR) =30.8 Hz),无法准确解释车轮多边形的常频现象[27]。采用考虑铁垫板振动的改进扣件模型获得的转向架车轮间钢轨3阶弯曲模态频率(592 Hz)与多边形激扰频率相吻合,解决了基于传统Kelvin扣件模型获得的钢轨局部弯曲共振与典型多边形存在2阶频率差异的问题。
3 轮轨耦合共振响应影响因素分析
轮轨耦合振动模态决定轮轨系统共振响应。我国高速铁路由于车型、轨道板类型及复杂运营环境影响,扣件间距、扣件刚度、轴距等存在差异,本节基于车辆-无砟轨道系统动力学模型分析这些因素对轮轨耦合共振响应的影响规律。
3.1 扣件间距
不同轨道类型的扣件间距有所差别,以扣件间距0.63、0.65 m作对比,扣件间距对摩擦功率和垂向力的影响规律见图10。
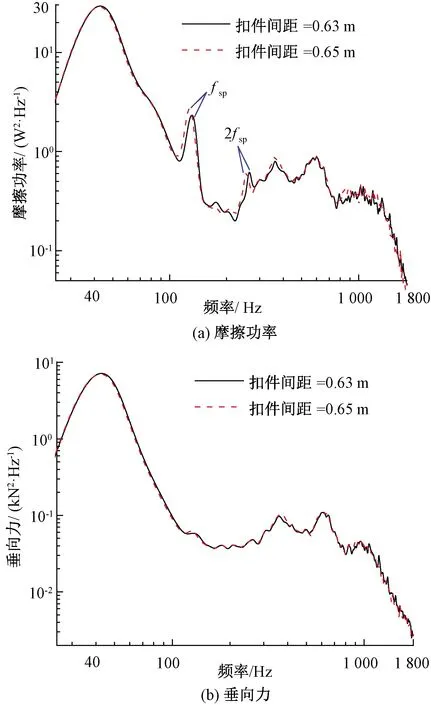
图10 不同扣件间距下轮轨耦合共振响应
由图10可知,轮轨动力响应除在扣件通过频率及其倍频处存在一定差异外,在其他频带处的变化不明显,可以推断扣件间距对轮轨耦合共振响应影响较小。
3.2 扣件刚度
扣件胶垫是温度敏感性材料,温度越低扣件刚度越高[28]。对比分析扣件刚度为30、90 kN/mm条件下的轮轨耦合共振响应,见图11。
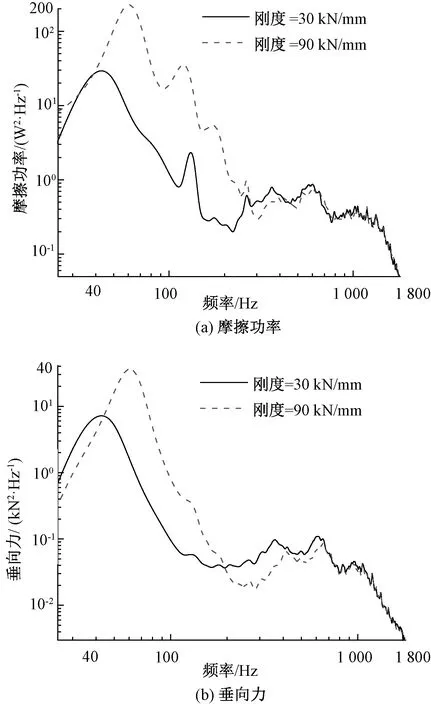
图11 不同扣件刚度下轮轨耦合共振响应
由图11可知,提高扣件刚度可大幅提高P2共振响应峰值及共振频带,同时会降低钢轨2阶、3阶弯曲共振响应并使相应共振频带向高频转移,而对pinned-pinned共振响应影响较小。因此,扣件刚度的提高虽增大P2共振响应峰值,但可降低钢轨3阶弯曲共振响应,减弱600 Hz附近轮轨周期磨耗的萌生。
3.3 轴距
轴距是影响钢轨局部弯曲模态的重要参数,参照我国动车组两种轴距参数:2.5、2.7 m,分析轴距对轮轨动力响应的影响,见图12。
由图12可知,当轴距由2.5 m增大至2.7 m时,P2共振保持不变,钢轨2阶和3阶弯曲共振响应减小并使得共振频带向低频转移,钢轨pinned-pinned共振响应在峰值上无显著差异仅在频域分布上有所不同。破坏单一波长磨损累积发展的基本条件可抑制轮轨周期性磨耗的形成,因此当不同轴距列车在同一线路上混合运行时,可降低钢轨上单一波长磨损的累积,将有助于减缓高速铁路上涌现的钢轨长波长波磨(激扰频率在600 Hz附近)的形成。
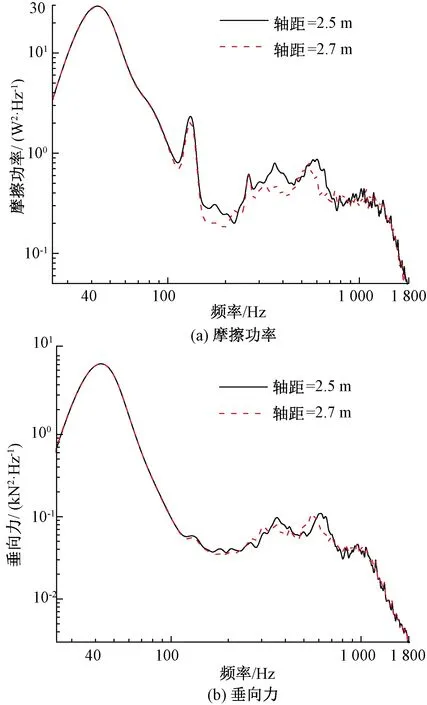
图12 不同轴距下轮轨耦合共振响应
4 结论
本文建立了车辆-无砟轨道系统动力学模型,求解了轮轨摩擦功率、垂向力在宽频范围内的分布特征,并和不同轮对作用下的仿真结果进行对比,确定了导致轮轨系统共振的轮轨耦合振动模态,并进一步分析了扣件间距、扣件刚度及轴距等因素对轮轨耦合共振响应的影响规律。具体结论如下:
(1)决定轮轨系统共振的轮轨耦合振动模态共有4种模式:P2共振模态以及转向架车轮间钢轨2阶弯曲、3阶弯曲和pinned-pinned振动模态,其分别导致摩擦功率在40~50 Hz、350~400 Hz、550~650 Hz、950~1 250 Hz处产生共振;垂向力在40~50 Hz、350~400 Hz、550~650 Hz、900~1 200 Hz处产生共振。
(2)轮轨耦合振动模态可分为两类:一类是车轮与钢轨作等幅同相振动的P2共振模态,其容易造成振动能量向车辆上部结构、轨下基础的传递,在全频段其共振响应峰值最显著;另一类是由于双车轮的约束作用使得转向架范围内钢轨产生了2阶弯曲、3阶弯曲及pinned-pinned振动模态,为钢轨局部弯曲模态,主要造成振动能量沿钢轨纵向在车轮间的传递及反射,其中钢轨3阶弯曲及pinned-pinned振动模态对诱导轮轨周期性磨耗的形成具有重要贡献。
(3)扣件间距对轮轨耦合共振响应影响较小;增大扣件刚度可大幅提高P2共振频率及响应峰值,而降低钢轨2阶、3阶弯曲共振响应并使得相应共振频带向高频转移;轴距对P2共振响应无影响,但轴距的增大可减弱钢轨2阶和3阶弯曲共振响应并使得相应共振频带向低频转移。扣件刚度及轴距的变化对钢轨pinned-pinned共振响应峰值影响不大。
综上所述,控制P2共振响应对降低车辆系统及沿线环境的振动具有积极意义,削弱高频区钢轨局部弯曲共振响应可在一定程度上抑制轮轨周期性磨耗的形成,而不同轴距列车在同一线路上混合运行将有助于降低高速铁路上涌现的钢轨波磨现象。此外,本文将车轮考虑成刚体,考虑轮对柔性对轮轨耦合振动模态及其动力响应的影响如何,下一步将重点进行研究。
