考虑地震动水力的高速铁路跨海斜拉桥行车安全性研究
2022-01-09雷虎军孙昱坤
雷虎军,刘 伟,孙昱坤
(福建工程学院 土木工程学院,福建 福州 350118)
近年来,随着我国高速铁路建设从陆地逐渐延伸到海洋,跨海桥梁已成为高速铁路线路的重要组成部分,尤其是斜拉桥结构,跨越能力强、刚度大,是高速铁路跨海桥梁的首选,例如正在建设中的福厦高铁泉州湾跨海大桥、安海湾跨海大桥都采用了斜拉桥结构[1]。我国东部和东南部沿海位于东南沿海地震带,且毗邻台湾海峡地震带,地震区密集。历史上在泉州、晋江、惠安等海域都发生过强震,给该地区造成了巨大的人员伤亡和经济损失。因此,沿海的高速铁路跨海斜拉桥及桥上列车面临地震的严重威胁。
关于地震引起的车桥耦合振动问题,近年来从简化的车辆模型到复杂车辆模型、从轮轨密贴假设到新型轮轨关系、从地震一致激励到多点激励,众多学者进行了系统研究,成果显著[2-6]。其中,对于铁路斜拉桥,熊建珍等[7]以天兴洲斜拉桥方案为例,分别针对货物列车、中速旅客列车和高速旅客列车进行了地震-车-桥仿真计算。韩艳等[8]通过建立地震作用下的列车-桥梁空间耦合振动模型,对列车通过某斜拉桥的全过程进行了仿真计算。朱志辉等[9]以某独塔斜拉桥为研究对象,采用等效荷载法计算车桥系统的地震响应,研究了桥上列车的行车安全性。相比普通铁路斜拉桥,高速铁路跨海斜拉桥面临深水环境,一旦发生地震,在桥梁下部结构会产生附加动水力,众多研究表明地震引起的附加动水力会改变结构的自振频率,对桥梁的动力响应影响显著[10-12]。然而,地震附加动水力对斜拉桥-列车系统动力响应的影响究竟如何,目前鲜有报道。
因此,要研究地震作用下高速铁路跨海斜拉桥的行车安全性,首先应解决车桥系统中地震动水力的计算问题。黄信等[13]基于辐射波浪理论,推导了深水桥墩的地震动水力计算公式,探讨了水底柔性反射边界的影响。王丕光等[14]推导了椭圆柱体地震动水力的精确解析解,并进行了验证。杜修力等[15]基于不可压缩水体辐射理论得到了圆形桥墩地震动水力的解析解,探讨了刚性柱法、Morison法和基频近似法3种简化方法的计算精度,研究表明刚性柱法的误差最小。郭婕等[16]从频域传递函数的角度探讨了上述3种地震动水力近似求解法的计算精度,并推荐使用刚性柱法。由于地震-列车-桥梁耦合系统模型规模大、非线性强,在系统中采用简化方法来模拟水-结构间的相互作用、计算地震动水力较为合理。
本文在以往研究的基础上[17],基于原有的地震-车-轨-桥耦合振动分析程序Ttbsas,采用刚性柱法模拟下部结构的地震动水力,并将其转换为节点附加质量,建立了考虑地震动水力的地震-车-轨-深水桥梁耦合振动模型,同时作为对比建立了不考虑地震动水力的耦合振动模型。以某跨海斜拉桥为例,通过输入3条实测地震波进行仿真计算,研究了地震动水力对车-轨-桥系统动力响应的影响,在此基础上分析了桥上高速列车的行车安全性。本文的研究成果可为高速铁路跨海斜拉桥的设计提供理论支持。
1 地震动水力简化计算方法
如图1所示,假设底部固定的悬臂圆柱体位于理想无黏性不可压缩水体中,水平地震波作用于柱底,忽略水体表面的自由波,则其运动方程为
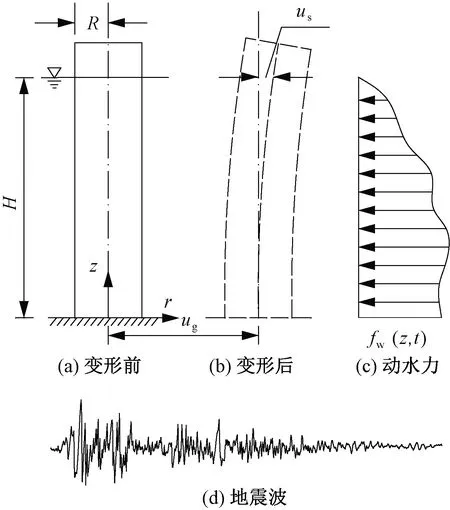
图1 水平地震力作用下的悬臂圆柱体
(1)
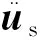
根据水体的控制方程和上述边界条件,即可推导该圆柱体在深度z处的精确地震动水力解[18]为
(2)
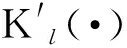
由此可知,精确的地震动水力是结构变形的函数。采用有限元法进行数值求解,则式(1)可采用向量和矩阵表达为
(3)
式中:
(4)
其中,Mw为动水力等效质量矩阵;N为单元的形函数。
将式(3)带入式(1)即可得到考虑地震动水力作用的结构运动方程为
(5)
采用刚性柱法进行简化计算[18]。在刚性柱法中,假设结构为刚体,则Mw中的项可简化为
(6)
Wang等[19]为便于工程应用,将式(6)中的级数求和进行了拟合,进一步简化为
(7)
(8)
式中:L=2R/H为圆柱体直径与水深之比。
将式(7)、式(8)计算的节点附加质量项带入式(5),即可求解考虑地震动水力作用的结构运动方程。由于上述推导是基于悬臂圆柱体,而实际工程中,矩形承台或桥墩应用非常广泛。赖伟[20]通过试验并采用最小二乘法拟合,得到了单位高度矩形截面的动水力附加质量与圆形截面动水力附加质量的等效换算系数为
(9)
式中:K为矩形截面换算系数,适用于0.1≤D/B≤10;D为矩形截面垂直于水流方向的宽度;B为平行于水流方向的宽度。
根据式(7)~式(9)即可计算圆形和矩形截面的动水力附加质量。
2 地震-车-轨-深水桥梁耦合振动模型
地震作用下的车-轨-深水桥梁耦合振动模型是在原有地震-车-轨-桥动力模型的基础上考虑地震时水与桥梁下部结构的相互作用形成的。因此,该模型包含原有的车辆、轨道、桥梁、轮轨关系、桥轨关系和地震力边界等模型以及新增的水-结构相互作用模型,见图2。
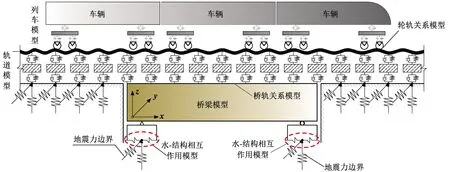
图2 地震-车-轨-深水桥梁耦合振动模型
在以往研究中基于新型轮轨关系假设和桥轨间的静力平衡条件建立了非一致地震激励下的车-轨-桥空间耦合振动模型,同时利用Compaq Visual Fortran平台编制了列车-轨道-桥梁-地震仿真分析程序Ttbsas[21],可以实现地震作用下任意桥型的车桥耦合振动仿真计算。基于此,将水-结构间的相互作用采用前述刚性柱法进行简化考虑,即可建立起地震作用下的车-轨-深水桥梁耦合振动模型,其运动方程可统一表达为
(10)
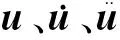
由式(3)~式(9)计算,联立求解方程式(10)即可得到地震作用下考虑地震动水力的深水桥梁-列车系统的耦合振动响应。
3 算例
3.1 计算参数
以某主跨400 m的双塔双索面半漂浮体系跨海斜拉桥为例进行仿真计算。桥梁全长940 m,跨度布置为(70+70+130+400+130+70+70) m,结构总体布置见图3。其中,桥上轨道采用CRTSⅡ型板式无砟轨道;主梁采用混凝土桥面板加槽型钢箱梁的叠合梁,宽16 m、高4.5 m;桥塔采用钻石型混凝土塔,塔高169.3 m,桥塔承台为矩形截面,尺寸为40 m×25 m,桥塔群桩基础的桩柱为圆形截面,直径为2.8 m;斜拉索采用镀锌平行钢丝索,按扇形对称布置72对。二期恒载取133.4 kN/m。
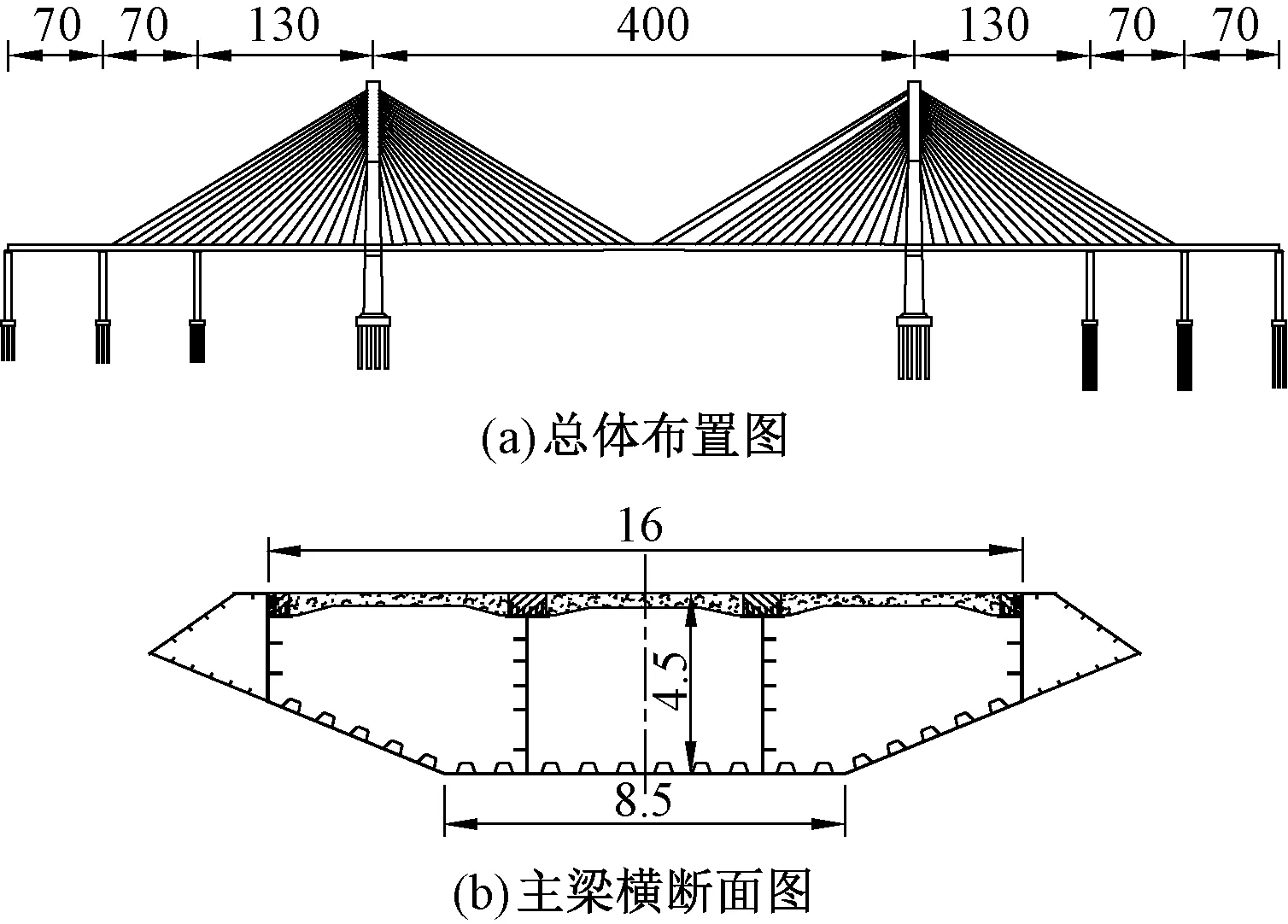
图3 主跨400 m高速铁路跨海斜拉桥(单位:m)
采用Midas Civil 2019分别建立两种斜拉桥有限元模型,即:考虑地震动水力(模型1)、不考虑地震动水力(模型2)。在模型1中,桥梁的局部冲刷线以上至最高水位线以下采用刚性柱法计算承台、桩柱的地震动水力附加质量,主塔的动水力附加质量计算结果见表1。
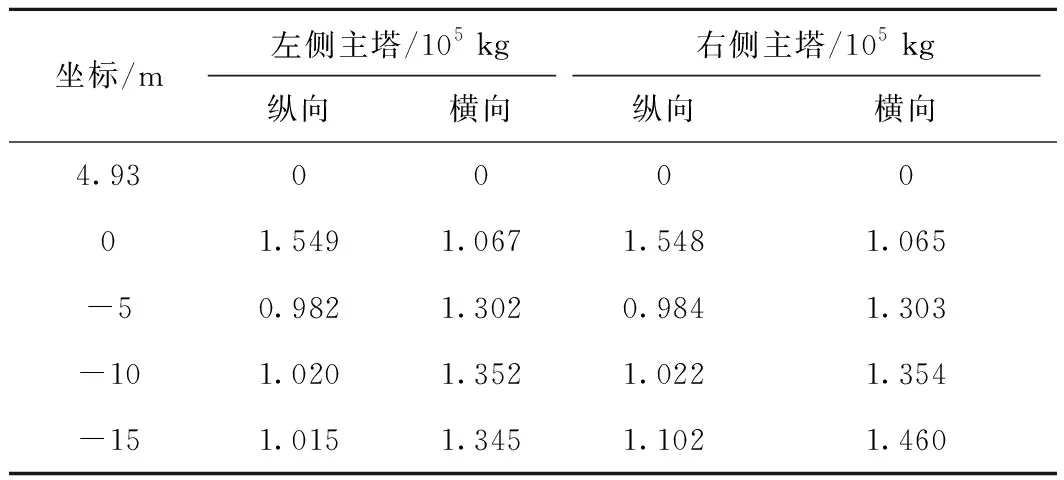
表1 动水力附加质量计算结果
采用子空间迭代法分别计算两种模型的自振特性,其自振频率对比见图4。由图4可知,两种模型的基频相同,均为0.145 Hz,且前10阶自振频率相差很小;考虑地震动水力后斜拉桥高阶模态的自振频率明显低于不考虑地震动水力时,且模态40~100为桥塔底部群桩的振型,这是由于考虑地震动水力后群桩的刚度不变而质量增大了。由此可见,地震动水力会显著影响斜拉桥的频率分布。将建立的两种斜拉桥模型导入Ttbsas程序,即可得到车桥计算的桥梁模型。
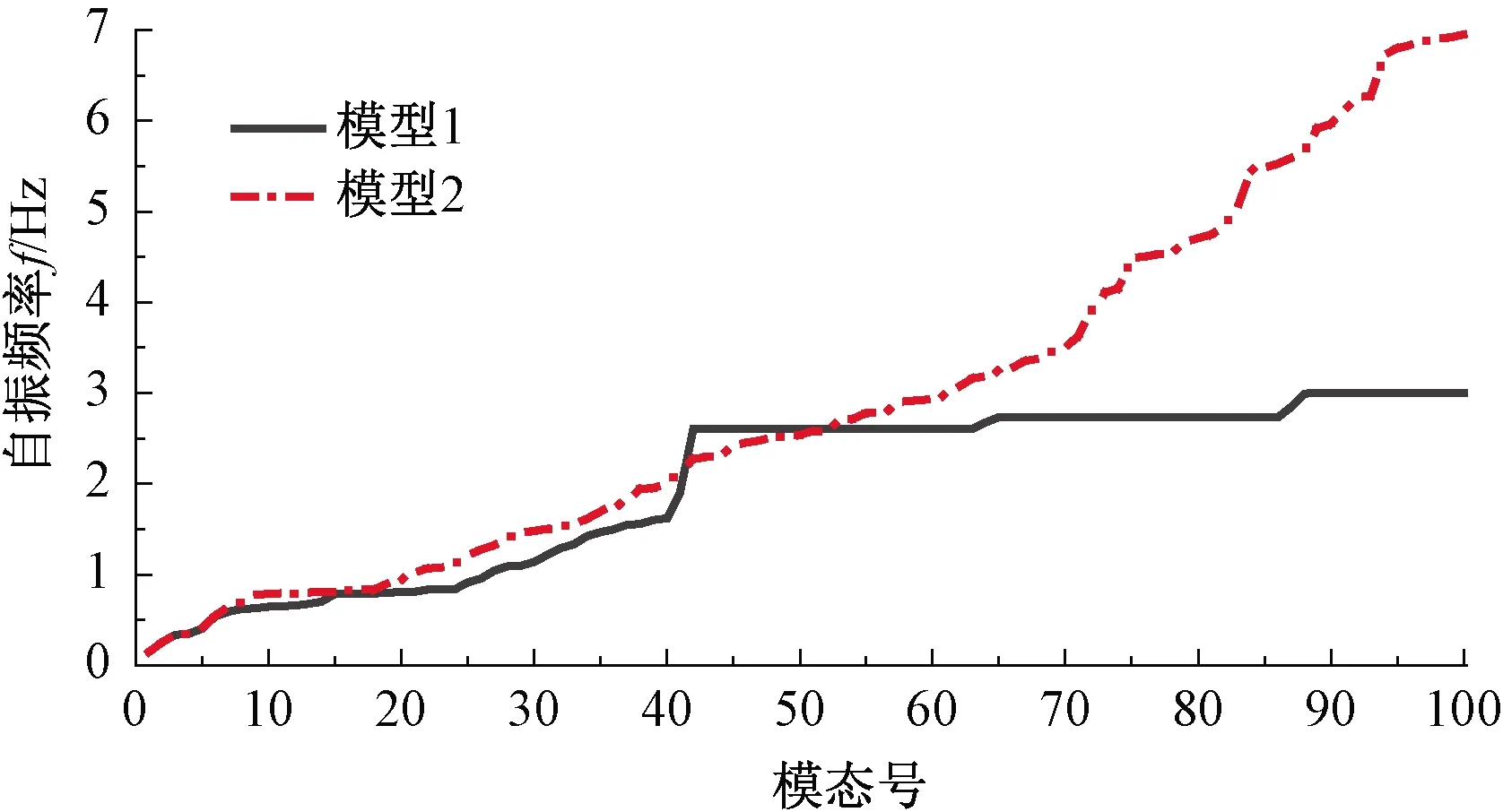
图4 两种模型自振频率对比
根据场地条件(Tg=0.45 s,设计地震PGA为0.15g),在太平洋地震工程研究中心选取3条典型地震记录作为输入,主要参数和加速度分别见表2、图5。
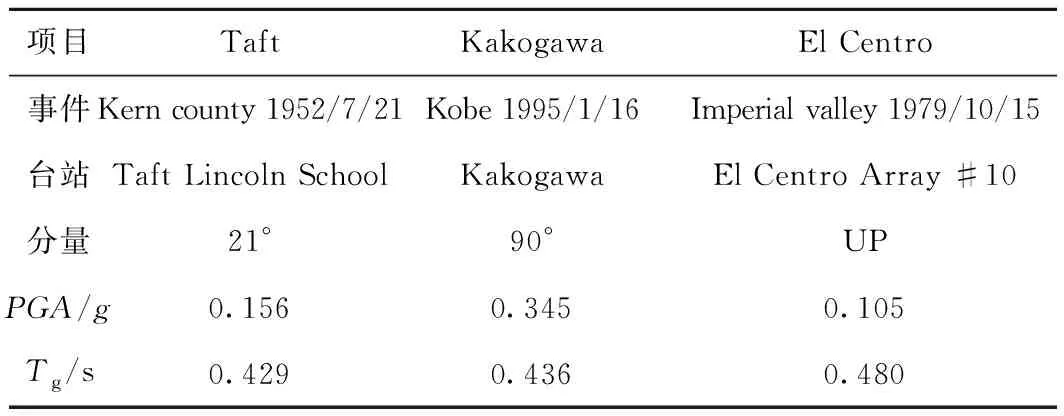
表2 地震波信息
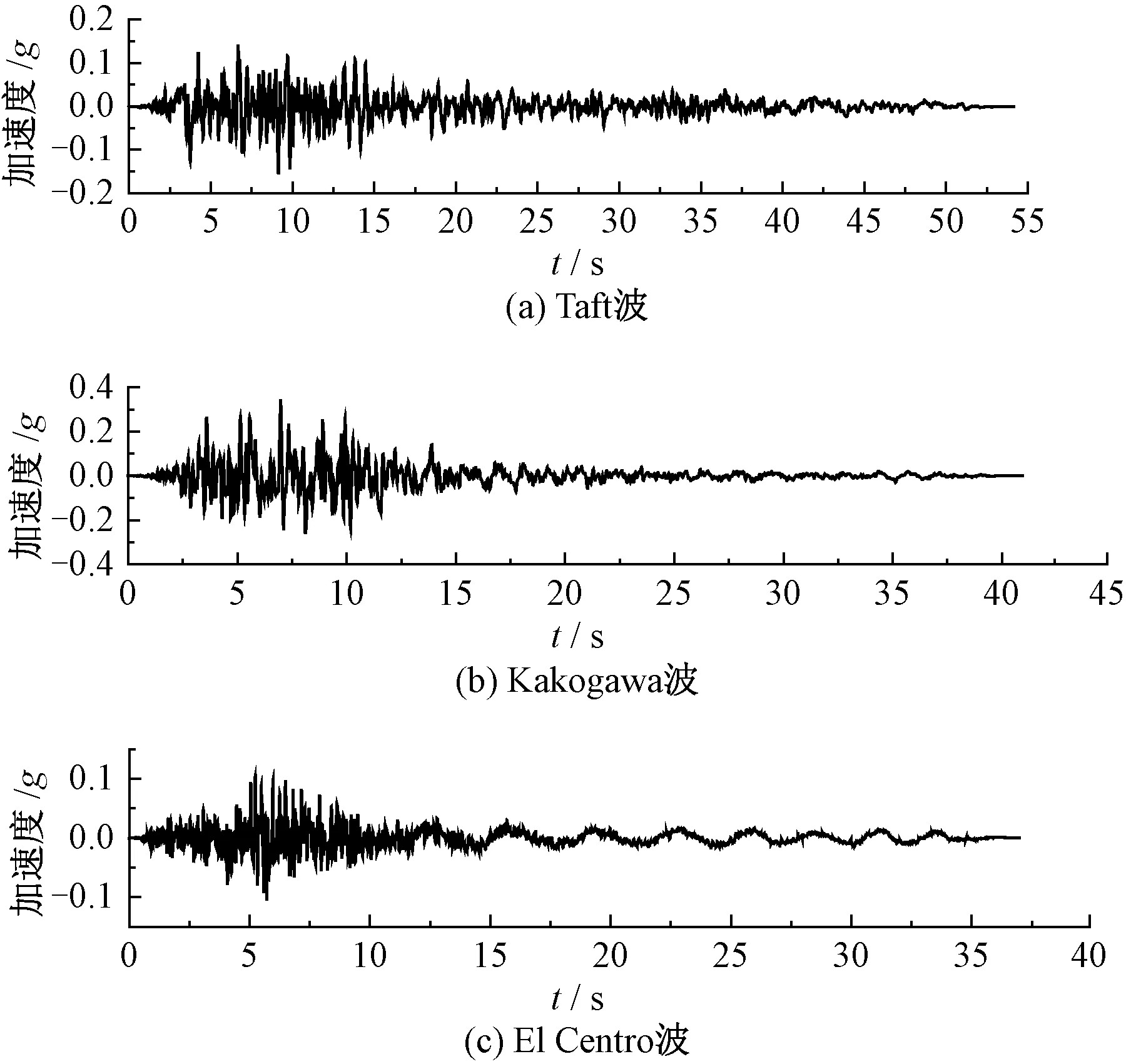
图5 地震波加速度时程
3.2 地震动水力的影响分析
根据建立的两种斜拉桥模型,首先输入Taft地震波,考察CRH3高速列车以时速350 km/h过桥时地震动水力对车桥系统动力响应的影响。横向和竖向地震动峰值加速度分别取0.1g和0.065g,假设地震发生时刻与列车上桥时刻相同。斜拉桥主梁跨中的横向位移和竖向位移时程见图6,主梁跨中断面左侧钢轨的横向位移和竖向位移见图7,列车的脱轨系数、轮重减载率和轮对横向力时程见图8。
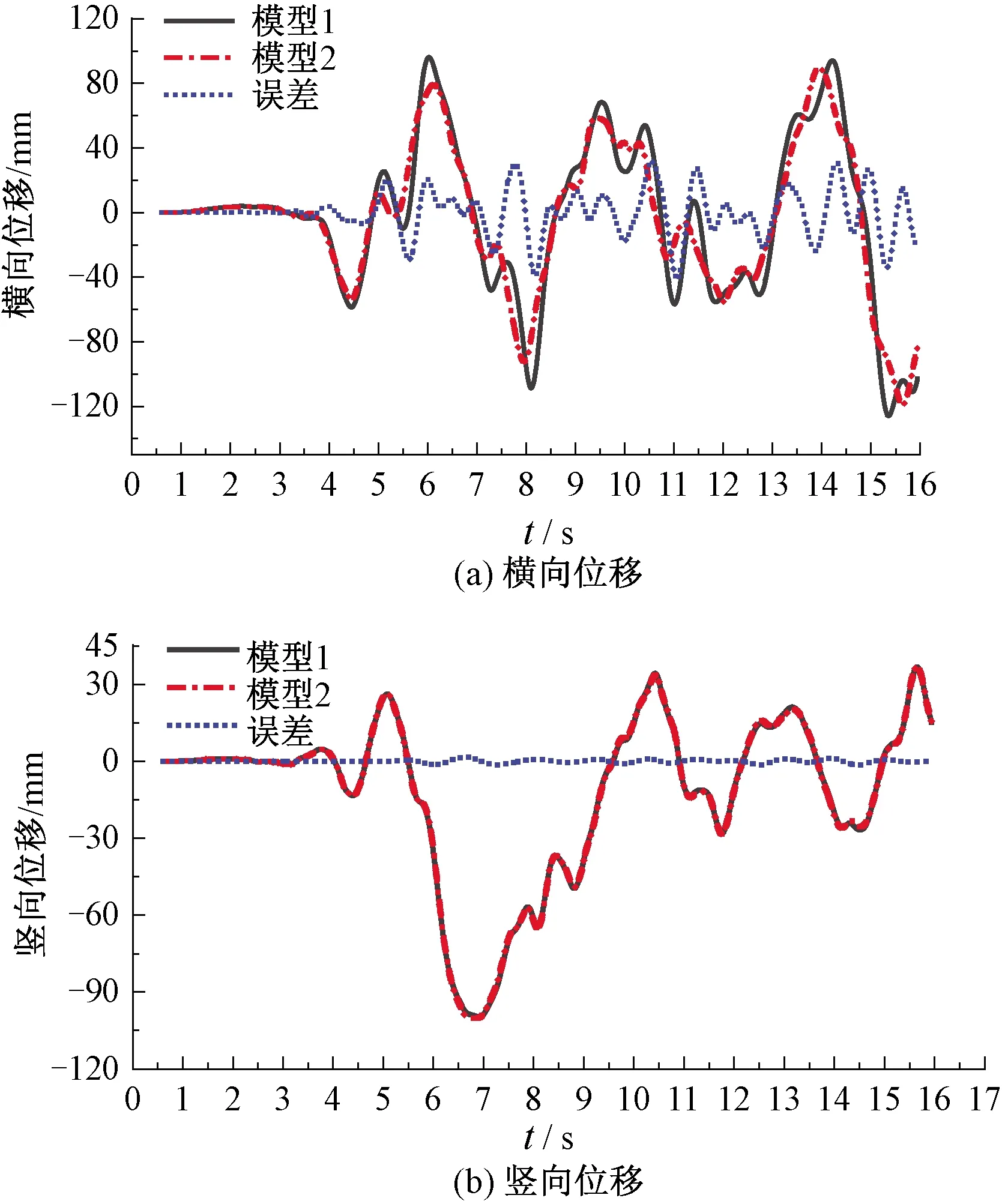
图6 主梁跨中位移时程对比
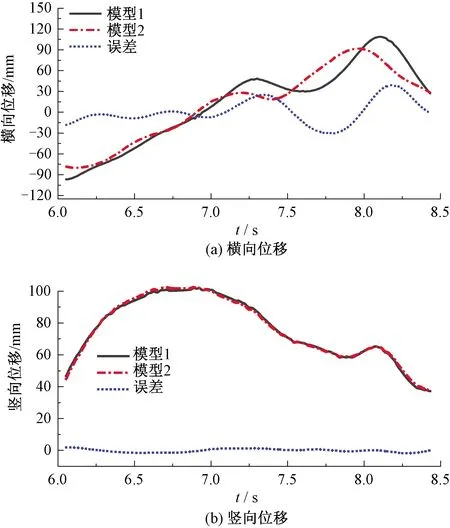
图7 主梁跨中左侧钢轨位移时程对比

图8 列车行车安全性指标时程对比
由图6可知,考虑地震动水力后斜拉桥主梁跨中的横向位移时程与不考虑时波形相似,但幅值不同,且考虑地震动水力后的幅值大于不考虑时。而对于斜拉桥主梁跨中的竖向位移,两种模型的差值趋于0。由此可见,地震动水力对斜拉桥主梁的横向位移影响较大,而对其竖向位移几乎无影响。
由图7可知,地震动水力对桥上钢轨的横向位移影响显著,且考虑动水力后,桥上钢轨的横向位移幅值大幅增加。此外,地震动水力对桥上钢轨的竖向位移影响不大,两种模型计算的钢轨竖向位移时程相差很小。
由图8可知,考虑地震动水力后轮轨间的脱轨系数、轮重减载率和轮对横向力的波形和幅值均差异较大,且考虑地震动水力后的幅值均大于不考虑时。由此可见,对于高速铁路跨海斜拉桥,不考虑地震动水力会低估列车过桥的行车安全性指标。
按照同样的方法对Kakogawa、El Centro地震波进行规格化处理,进一步考察不同地震波作用下地震动水力对车桥系统动力响应的影响。两种斜拉桥模型主梁跨中的动力响应幅值对比见表3,列车的行车安全性指标幅值对比见表4。

表4 列车行车安全性指标幅值对比
由表3可知:①不考虑地震动水力会使计算得到的桥梁横向位移、桥梁横向加速度和钢轨横向位移偏小。对于本文的计算条件,主梁跨中断面的横向位移、横向加速度和钢轨横向位移的平均值分别偏小6.4%、30.0%和17.7%。②两种模型的竖向动力响应幅值的相对误差均小于1%。分析原因可知,考虑地震动水力后,斜拉桥下部结构与水接触部分的纵横向质量增加了,而其竖向质量无变化,这会改变斜拉桥的纵横向自振特性,而对其竖向振型几乎无影响。
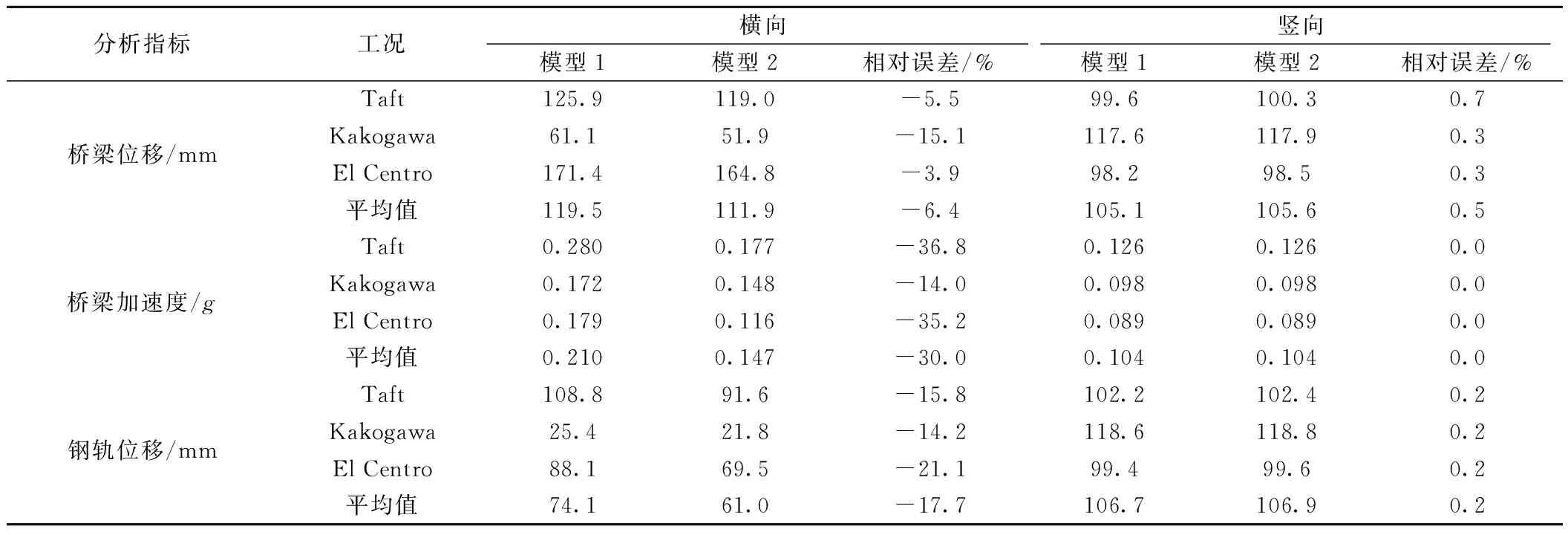
表3 主梁跨中断面动力响应幅值对比
由表4可知:①不同地震波作用下,不考虑地震动水力会使计算得到的脱轨系数幅值、轮重减载率幅值和轮对横向力幅值偏小。对于本文的计算条件,3条地震波作用下的平均值分别偏小4.5%、4.4%和6.0%。②不同地震波作用下,地震动水力对桥上列车的行车安全性指标的影响大小不同。例如,不考虑地震动水力时Taft、Kakogawa、El Centro地震波作用下的脱轨系数分别偏小7.8%、3.4%、1.8%。这是由于地震动水力改变了桥梁结构的纵横向自振频率,而不同地震波包含的频率成分不同,因此其影响大小也不一样。由此可见,在研究地震作用下高速铁路跨海斜拉桥的行车安全性时需输入多条地震波进行综合评判。
综上所述,对于高速铁路跨海斜拉桥,不考虑地震动水力会低估桥梁、桥上轨道的横向动力响应以及列车的行车安全性指标,可能造成对桥上列车行车安全的误判。
3.3 行车安全性讨论
根据前述分析,对于高速铁路跨海斜拉桥,地震动水力的影响不可忽略。本节考虑地震动水力的影响,以模型1为分析对象,考察不同水平地震发生时过桥车辆的行车安全性。分析中,列车过桥的车速取275~375 km/h、间距为25 km/h,地震动峰值加速度分别取0.05g、0.10g、0.15g以及无震4个水平。根据TB 10002—2017《铁路桥涵设计规范》[22],采用指标1~指标3来评判列车过桥时的行车安全性,其限值为
(11)
式中:Q为轮轨横向力;P为轮轨垂向力;ΔP为轮重减载量;P0为车轮静轮重。根据车辆参数,Q的限值为57.69 kN。不同强度地震作用下脱轨系数、轮重减载率和轮对横向力幅值随车速的变化曲线见图9,图9中幅值为3条地震波计算的绝对最大值。
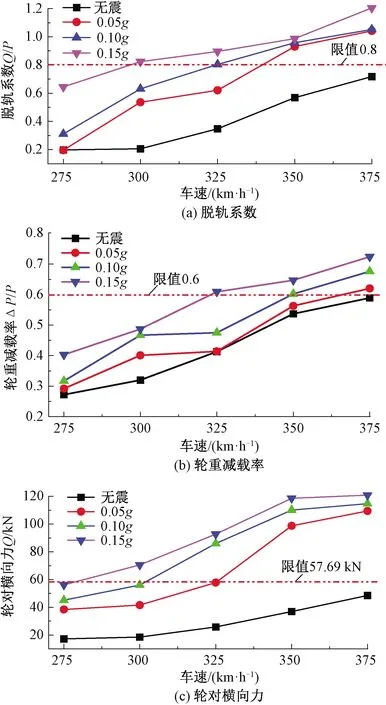
图9 列车行车安全性指标随车速的变化曲线
由图9可知,列车的脱轨系数、轮重减载率和轮对横向力幅值均随地震动峰值加速度的增大而增大,且列车过桥的车速越快,其幅值也越大。由此可见,对于高速铁路跨海斜拉桥,地震动峰值加速度和车速是影响桥上列车行车安全的两个主要因素。根据各个指标的限值,可以得到高速列车过桥时的安全车速阈值,见表5。
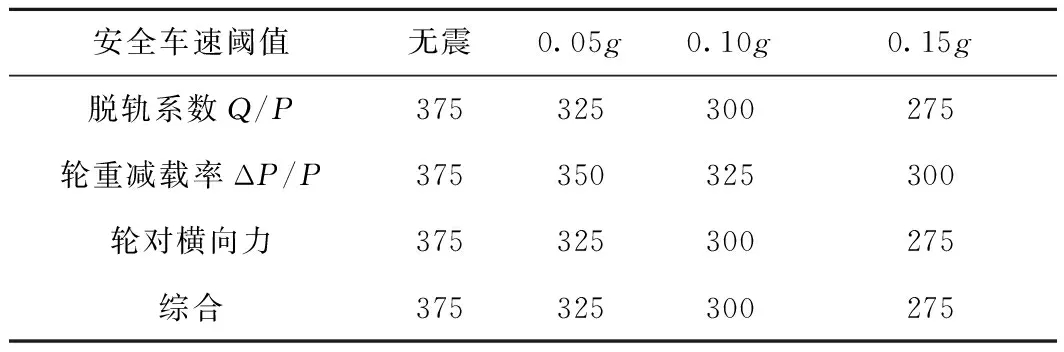
表5 列车安全车速阈值
在表5中,采用不同指标得到的安全车速阈值有差异,因此可综合3个指标来共同评判列车过桥时的行车安全性。其中,无震时的安全车速阈值为375 km/h,而0.05g、0.10g、0.15g三个水平地震作用下的安全车速阈值分别为325、300、275 km/h。由此可见,无震时高速列车以设计车速350 km/h通过该跨海斜拉桥是安全的,而多遇地震(0.05g)和设计地震(0.15g)下高速列车过桥时的安全车速分别降低到设计车速的92.9%和78.6%。
4 结论
本文在已有程序Ttbsas的基础上,采用刚性柱法计算地震动水力,研究了地震作用下高速铁路跨海斜拉桥的行车安全问题。得到了以下几点结论:
(1)地震动水力对高速铁路跨海斜拉桥及桥上钢轨的横向动力响应影响显著,而对其竖向动力响应几乎无影响。对于本文的计算条件,不考虑地震动水力会使主梁跨中断面的横向位移、横向加速度和钢轨横向位移分别偏小6.4%、30.0%、17.7%。
(2)对于高速铁路跨海斜拉桥,不考虑地震动水力会使桥上的列车行车安全性指标偏小,可能造成对桥上列车行车安全的误判。对于本文的计算条件,列车的脱轨系数、轮重减载率和轮对横向力会分别偏小4.5%、4.4%、6.0%。
(3)对于高速铁路跨海斜拉桥,桥上列车的安全车速阈值随地震动强度的增加而降低。对于本文的计算条件,无震时的安全车速阈值为375 km/h,而0.05g、0.10g、0.15g三个水平地震作用下的安全车速阈值分别为325、300、275 km/h。
本文针对高速铁路跨海斜拉桥分析了地震动水力的影响,但研究中忽略了水面波浪的作用。这对于大部分浪高小、波浪作用不突出的海湾桥梁是适用的,但对于一些波浪作用不能忽略的高速铁路跨海桥梁,还需研究地震-波浪联合作用下的车桥耦合振动问题。
