市域快速轨道交通快慢车运行组织下越行站设置方法及模型研究
2022-01-09高国飞张星臣陈修全
高国飞,张星臣,陈修全,郑 汉,2
(1.北京交通大学 交通运输学院, 北京 100044;2.北京城建设计发展集团股份有限公司 城市轨道交通绿色与安全建造国家工程实验室, 北京 100037)
随着城市化进程的加快,城市从中心向外逐步扩张,卫星城及新城不断发展,居民的出行范围日益扩大,进而引发了出行时间较长的问题。为满足居民在城市中心区与郊区之间便捷出行,减少居民出行时间并带动市郊城市化发展,近年来各大城市开始规划建设市域快速轨道交通。快慢车组合运营方案是市域快速轨道交通常用的运营组织模式,相比传统的站站停方案,在提高旅行速度、加快车底周转、提高乘客出行效率等方面具有较大优势。慢车主要满足沿线各站点乘客的出行需求,快车主要满足长距离乘客的出行需求。减少快车停站可有效缩短旅行时间,但为吸引更多客流还需设置必要数量的停靠站。越行站选择规则是一系列离散的判断准则,当同时考虑通过能力、发车间隔以及快慢车开行数量时,如何设置越行站成为难点。合理的越行站数量及位置,对于压缩行车间隔、提高运输效率、合理配置资源、充分发挥城市轨道交通大运量运输的优势具有重要意义。
国外对于快慢车组合运营的研究起步较早,主要分析快慢车组合运营优缺点,以及结合各类客流特点设计不同的快慢车停站方案及列车时刻表。Lee等[1]研究了快慢车运营的优缺点,利用遗传算法建立快慢车停站模型。Jamili等[2]研究了不同客运需求情况下快慢车的运营模式,以旅客最小出行时间为目标,考虑客流波动,提出一种新的鲁棒数学模型和模拟退火算法求解快慢车停站方案。Nomura等[3]提出考虑快慢车最小发车间隔时间的列车时刻表优化方法。Mignone等[4]在保证线路上各站列车到发时刻基本不变的前提下,优化分时段开行快慢车的跨站停站方案,以满足沿线各站在时间上分布不均衡的旅客乘降量。国内对快慢车运营组织的研究方法主要有运行图铺画法、理论计算法和模型优化法3种。运行图铺画法直观精确,但效率较低,宋键等[5]、刘丽波等[6]等利用该方法确定了越行站的合理位置;理论计算法根据起终点的距离及时间目标要求,计算旅行速度,再根据车型和站间距的相互关系确定站间距,并根据线路条件确定越行站的位置,具有方便快捷的特性,在现场广泛应用。张国宝等[7]研究了3种行车组织方案及其适用的客流特征,提出了一种判定列车是否越行及越行站设置数量和位置方法。汤珏等[8]认为快慢车发车间隔、开行密度为市域线采用快慢车运输组织方式时越行站的确定的主要影响因素,并提出快慢车开行比例1∶1且快车均匀发车的情况下越行点的设置公式,其他开行比例的情况下,在此基础上进行调整。谭小土[9]、祝晓波[10]使用该方法提出了越行的判定条件以及越行站数量和位置的确定框架。第3种方法是考虑车辆运用、运输成本、总体时间效益等因素,建立模型进行站点的优化和选择,如张鹏等[11]以乘客总节约时间最大为目标函数,以运营成本和客流量为约束条件建立模型并求解。张香明等[12]建立越行站的工程造价、乘客的总出行时间和企业运营成本构成的总成本最小的目标函数,研究市域快速轨道交通越行站设置的数量及位置,以确定快慢车运输组织方案,得出越行站设置方案。唐禄林等[13]以地铁快慢车运输组织模式下乘客总出行时间和企业运营成本最小为目标函数建立模型获得停站方案。
既有研究还存在一些不足之处。通过铺画运行图确定越行站位置的方法在方案设计阶段由于部分因素未完全确定,参数的简单变动也将导致重新铺图,工作量大,在方案设计阶段一般不采用;而模型优化的方法操作复杂,求解难度大,不适合设计阶段大量方案的快速比选。因此对理论计算法进行补充和发展较符合设计实际需求。本文以市域快速轨道交通单向线路为对象,研究客流需求分布和快车停站方案基本确定情况下的越行站设置算法,以列车最小间隔时间、快慢车开行数量、快车越行节约时间、列车在各站的停站时间以及通过能力等因素对快慢车越行站位置的影响为输入,明确给出越行站设置的判定规则。综合考虑预设的快车停站方案,设计确定越行站数量及各越行站位置的启发式算法。研究成果可为设计阶段越行站的布置提供理论依据和方法。
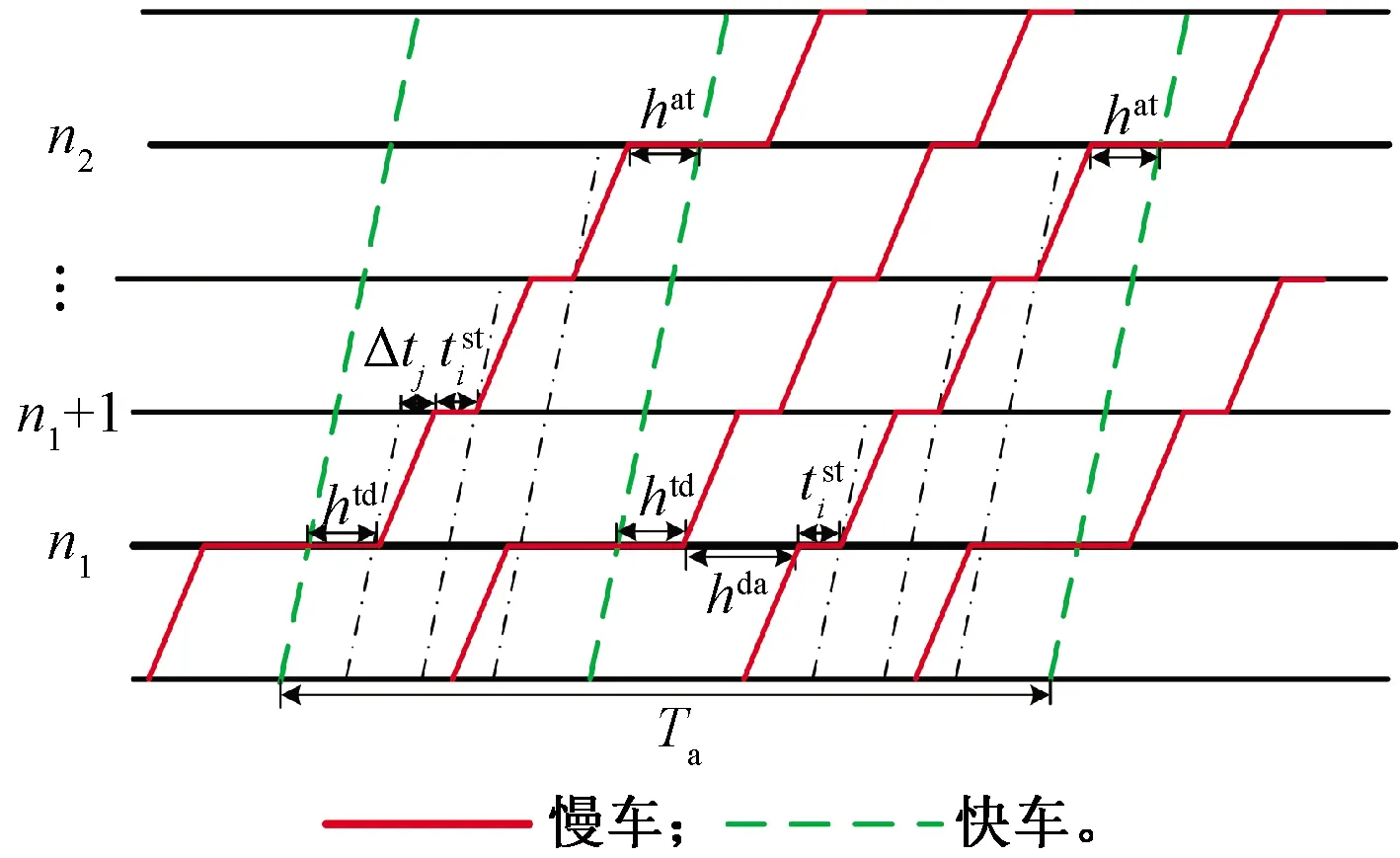
1 快慢车越行站设置规则
快车越行慢车时,会造成慢车在越行站的等待,降低乘客的出行体验,而且设置较多的越行站会提高建造成本,所以越行站布局设置的目标是在满足客流需求的条件下,尽可能地减少越行站数量,增大越行站间距。又由于快慢车在越行站受到车站间隔时间的约束,二者必须在车站保证一定的到达和发车间隔时间。下面在通过能力、列车到达和出发间隔时间等条件的约束下,分析越行站设置的具体规则和方法。
1.1 越行的判断规则
一般情况下,在线路上开行的快车和慢车是同一种车型,快车比慢车节省的时间主要是慢车的制动时间、停站时间和启动时间,而与区间长度无关,因此快车和慢车在第j个区间运行的时间差Δtj可以认为是相同的[14],tj为列车在区间j的运行时间。
快慢车越行时间关系见图1。如图1所示,列车在车站A和B之间运行,如前行列车为站站停慢车,后行列车为快车,tl为站站停慢车在该区间的运行时间,该运行时间由区间纯走行时间和停站时间组成,即
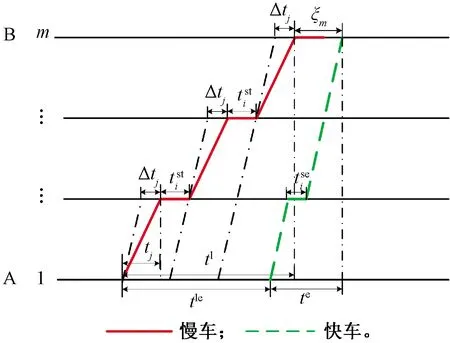
图1 快慢车越行时间关系
(1)
(2)
式中:ai为0-1变量,若快车在第i个车站不停车为0,否则为1。
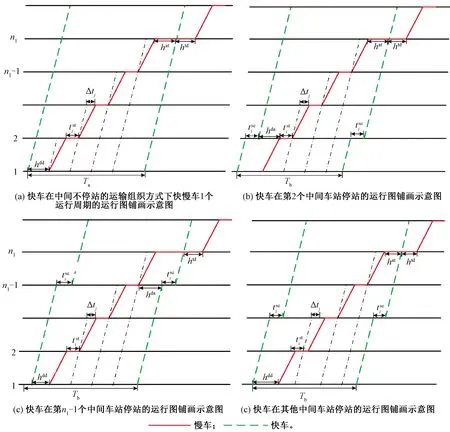
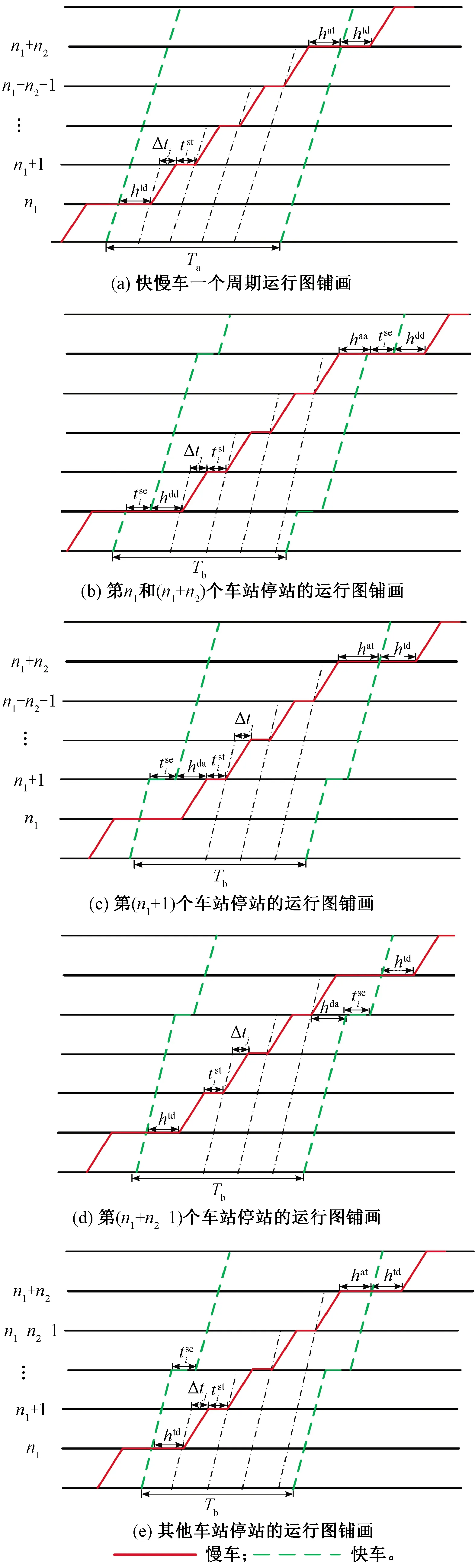
判定后行列车是否会越行前行列车,应判断慢车和快车在车站的到达间隔是否能满足列车在车站的最小间隔时间。ξm为快车和慢车在车站m的到达间隔时间,ht为列车在车站的最小间隔时间,包括最小到通间隔时间、最小发通间隔时间、最小到达间隔时间、最小发车间隔时间等。当ξm≥ht时,后行列车在A—B站间不发生越行;当ξm-1≥ht且ξm (3) 式中:Ile为慢车与快车的发车间隔时间。 假定快慢车开行数量比为q:p(q,p均为整数),当快车开行数大于慢车时(q>p),会出现快车连续铺画的情况,这种情况实际很少存在。本文仅研究快车开行数小于等于慢车(q≤p)且快车不连发的情况。这种情况下,有快车在中间站不停站和快车在中间站停车两种组织方式。 1.2.1 快车在中间不停站 慢车与慢车的发车间隔为Ill,快车与慢车的发车间隔为Iel,最晚出发的快车和最晚出发的慢车发车间隔时间为Ile,见图2。当快车少于慢车时,快慢车交替铺画方案见图3。 图2 越行站位置与快慢车越行的关系 图3 快车少于慢车时快慢车交替铺画(q∶p=2∶3) 假定快车在第n1车站越行慢车,则慢车与快车的最小发车间隔Ile为 (4) (5) 根据推算,这种情况下的线路通过能力为[15] Na=3 600(q+p)/Ta 1≤q≤pn1>2n2≥2 (6) 式中:Na为快车在中间站不停站运输组织下,单位时间内通过的列车数量;Ta为快车在中间站不停站运输组织下,1个快慢车组合的运行周期时间;hda为前车出发,后车到达的最小发到间隔时间。 要确定越行站的位置,就是在已知发车间隔时间Ile和线路通过能力N的前提下计算n1和n2的值,则需按照式(4)~式(6)进行计算。应从前行方向第2个越行站位置开始,可将前一越行站位置记为n1,然后对照式(5)和式(6)来计算后一越行站的位置,直到后续没有符合条件的车站为止。 (7) 同理由式(5)和式(6)可得n2为 (8) 式中:⎣·」表示向下取整。 1.2.2 快车在中间停站 图4 快车不同停站方式运行周期对比 a2·(hdd+Δt1-hda)-an1-1· (hat+Δtn1-1-hda)n1>2 (9) 式中:hdd为在同一车站,前车出发,后车出发的最小发车间隔时间。 图5 越行组织方式下快车不同停站方式周期对比 (10) an1+1·(Δtn1+htd-hda)-an2-1·(Δtn2-1+hat-hda) n1,n2>2 (11) 式中:Nb为快车在中间站停站运输组织下,单位时间内通过的列车数量。 以列车最小间隔时间、快慢车在各区间的时间差等运行图参数,根据客流情况确定的快慢车开行数量、列车在各站的停站时间等客流因素为输入条件,研究越行站设置模型和算法。模型以设置最少的越行站数量(即最大越行站间隔)为目标,目标函数为 (12) 式中:nx为决策变量,表示第x个越行站的位置,nx-nx-1表示相邻越行站的间隔x∈[2,θ],nx≠0。 由于计算前无法确定越行站具体数量,模型中引入越行站的上限θ,则模型的解为向量Nx={nx},x∈[1,θ]。 模型的基本约束为 (hdd+Δt1-hda)-an1-1·(hat+Δtn1-1-hda)≤Ile (13) anx+1·(Δtnx+htd-hda)-anx+1· (14) 2≤nx≤m-1 (15) 1≤x≤θ (16) 上述约束中,快车停靠站的确定应以客流预测为基础,综合考虑车站周边规划,车站功能及级别、各时段总客流乘降量、换乘量等因素,将组团中心站点、换乘站、特殊功能站点、重要客流集散点确定为快车停靠站。同时可根据发挥特定速度效率需要的站间距以及越行站个数进行适当增减。 由于初始越行站位置、与快车停站的位置关系和越行站数量均难以确定,且相互关联的变量多,因此适合采取启发式方法求解。基本思路是从第2个车站开始(n1=2),沿线路方向对车站进行搜索,逐步累加nx的取值,若nx的设定能满足模型中的通过能力及发车间隔等约束,则继续向前搜索;若nx的取值无法满足约束,则设定新的越行站,使快慢车可以在此交汇,并更新x→x+1。该过程一直迭代,直到搜索至终点站m或设置的越行站数量达到上限θ。 对于快车在中间站不停站组织方式,可以直接通过式(4)~式(6)得到越行站设置方案。 具体算法如下: Step2初始化。车站计数从第1个车站开始,即i=1;区间计数从第1个区间开始,即j=1;以nx代表列车的越行站位置,令x=1,根据2.2小节中的越行规则寻找n1的位置;记初始累加总计为hat+Δt1,即sum=hat+Δt1。 Step3确定第1越行站初始解。当累计总加sum小于等于期望发车间隔Ile时,即sum≤Ile: Step3.1车站计数加1,即i=i+1;区间计数加1,即j=j+1。 Step4在考虑快车是否停站的情况下,验证第1越行站是否需要更新。 Step4.1将结果记为第1越行站初始解,n1=i。 Step5重新确定第1越行站。当累计总加sum小于等于期望发车间隔Ile时,即sum≤Ile: Step5.1车站计数加1,即i=i+1;区间计数加1,即j=j+1。 Step6将第1越行站的位置更新,n1=i。若与Step4确定的位置相同,则n1为第1越行站的最终解;否则,回到Step4重新对于第1越行站位置进行修正。 Step7确定后续越行站,当越行站设置数量仍在预设范围内时,即nx≤m,x≤θ: Step7.2.1车站计数加1,即i=i+1;区间计数加1,即j=j+1。 Step7.4重新回到Step7.2,重新计算得到i值,若与上次相同,则在第i站设置越行站,nx+1=i;若两次不同,则重复Step7.3、Step7.4,直至两次i值相同,记nx+1=i。 Step7.5x=x+1。 Step8输出结果。越行站序列Nx={nx},nx∈[2,m-1] 设计的算法经Python语言实现,以通用计算工作站为平台,在解决不同线路(包含10至20座车站)的越行站设置问题时平均计算时间在2 s左右,符合设计业务的计算效率要求。 可知,若该线快车不越行,慢车与快车的发车间隔应大于12.5 min。该发车间隔会让乘客等待时间太长,同时不满足市域快速轨道交通的服务水平要求,因此,该线需要组织快慢车运输组织。 根据线路实际客流情况、各站OD量及断面量情况,取快慢车开行数量比为1∶4,N=24对/h,根据断面客流情况,取慢车和快车的发车间隔时间Ile=180 s。 3.1.1 计算第1越行站位置 根据算法Step1—Step6,将N=24对/h、Ile=180 s、p∶q=1∶4时,代入式(9)计算可得n1=3,由于a2=0,始发站与第1越行站n1之间无快车停站,所以无需对n1进行修正,第1越行站设置在车站3。 3.1.2 计算第2越行站位置 根据算法Step7,将N=24对/h、Ile=180 s、p∶q=1∶4、n1=3和ai=0代入式(10)、式(11),计算可得n2=7,由于a6=1,第1越行站与第2越行站之间存在快车停站,所以进行系数修正。将a6=1、a4=a5=0重新代入式(10)、式(11),第2次计算结果n2=8,第1次与第2次计算结果不同,所以继续修正系数。将a6=1、a4=a5=a7=0重新代入式(10)、式(11),第3次计算结果n2=8,第2次与第3次计算结果相同,所以将车站8设置为第2越行站。 3.1.3 计算其他越行站位置 从第2个越行站位置开始,都可将前一越行站位置记为n1,然后对照式(10)、式(11)来计算后一越行站的位置,直到后续没有符合条件的车站为止。计算可得:当N=24对/h、Ile=180 s、p∶q=1∶4时,需在车站3、8、13依次设置越行站。 对于3.1节中的案例,取快慢车开行数量比为1∶4,N=24对/h,慢车和快车的发车间隔时间Ile=390 s。分别考虑快车不停站与快车停站(仅停站6和站11)两种情况,计算越行站设置方案,快车在中间站不停站时,需在车站7、11、15依次设置越行站;快车在中间站停站时,需在车站8、13依次设置越行站。由此可见,当有快车在中间站停站时,始发站与第1越行站,以及后续相邻越行站之间的间隔均会增大。这是由于在有快车在中间站停站的情况下,通过式(9)与式(11)计算得到的发车间隔Ile与周期T相较于不停站情况均更小,所以当单位小时列车开行数量一定时,可以允许更大的越行站设置间隔。 为研究提出算法与不同参数的关联特性,进行灵敏度分析。由于实际运营中快慢车开行数量差别不宜过大,本文选取快慢车开行数量比分别为1∶5、1∶4、1∶3、1∶2、2∶4、2∶3、3∶4、1∶1,慢车和快车的发车间隔时间Ile变化范围为2~8 min,线路通过能力N∈{22,24,26}对/h为例对越行站位置进行计算和分析。通过依次变化快慢车开行数量比、慢车和快车的发车间隔时间Ile以及线路通过能力N,计算得到不同情况下越行站设置位置,总结归纳不同因素对于越行站设置的影响规律。 3.3.1 固定慢车与快车发车间隔时间Ile和线路通过能力N 将慢车与快车发车间隔时间Ile和线路通过能力N固定,分析快慢车开行数量比对于越行站设置数量以及位置选择的影响,计算结果见图6。 图6 固定Ile和N情况下的越行站设置方案 当慢车发车数量一定,快车发车数量逐渐增加时,可以看出第1越行站n1的设置位置并没有随快车数量的增加而变化;之后的越行站位置随着快车数量的增加布置越来越紧凑,不过快车数量增加到一定程度时,对越行站位置的影响也越来越小。此外,随着快车数量逐渐增大,相同区间内需设置的越行站数量也越来越多。当快车的发车数量一定,慢车发车数量逐渐增多时,可以看出第1越行站n1的设置并没有随慢车数量的增加而变化;之后的越行站随着慢车数量的增加,相邻越行站之间的间隔也越来越大。此外,随着慢车数量逐渐增大,相同区间内需设置的越行站数量也越来越少。 综上,在慢车与快车发车间隔时间Ile和线路通过能力N一定的情况下,快慢车数量的变化不会对第1越行站n1位置的设置产生影响,但越行站的数量和紧密程度会随着快慢车数量的变化而变化,快车数量的增加和慢车数量的减少都会使越行站设置数量越来越多,相邻越行站之间的间隔越来越小。相反,快车数量的减少和慢车数量的增加会使越行站设置数量越来越少,相邻越行站之间的间隔越来越大。 3.3.2 固定快慢车开行数量比和线路通过能力N 将快慢车开行数量比和线路通过能力N固定,分析快慢车发车间隔时间对于越行站设置数量以及位置选择的影响,计算结果见图7。 由图7可知,随着慢车与快车发车间隔时间Ile的逐渐增大,第1越行站n1的设置位置距离始发站越来越远,后续越行站的位置也随着第1越行站n1的位置而向后推移。此外,相邻越行站的间隔没有随着慢车与快车发车间隔时间Ile的变化而变化,所以随着慢车与快车发车间隔时间Ile的逐渐增大,在同一区间内越行站的数量也越来越少。 图7 固定快慢车开行数量比和N情况下的越行站设置方案 3.3.3 固定慢车与快车发车间隔时间Ile和快慢车开行数量比 将慢车与快车发车间隔时间Ile和快慢车开行数量比固定,分析线路通过能力N对于越行站设置数量以及位置选择的影响,计算结果整理见图8。 图8 固定Ile和快慢车开行数量比情况下的越行站设置方案 随着线路通过能力N的逐渐增大,可以看出第1越行站n1的位置始终保持不变,后续越行站之间的间隔越来越小,布置越来越紧凑,因此越行站的数量也随着线路通过能力N的增大而增加。 3.3.4 相邻越行站间隔的灵敏度分析 在慢车与快车发车间隔时间Ile和线路通过能力N一定的情况下,研究快慢车数量对相邻越行站之间的间距产生的影响,计算结果见图9。 图9 固定Ile和N情况下的相邻越行站间隔设置 显然,随着快车数量的增加以及慢车数量的减少,相邻越行站之间的间隔也会逐渐变小。并且,当快车数量较少时,快慢车数量的变化对于越行站间距的影响比较明显,随着快车数量的增加,这种影响变得越来越小。 在慢车与快车发车间隔时间Ile和快慢车开行数量比一定的情况下,研究线路通过能力N对相邻越行站间距产生的影响,计算结果见图10。显然,线路通过能力N越大,相邻越行站间隔越小,因此,必须缩短越行站间距来满足较高通过能力的要求。 图10 固定Ile和快慢车发车情况下的相邻越行站间隔设置 越行站设置的主要控制性指标包括越行站数y、第1越行站n1以及越行站间隔Δn。设三者均与能力N、发车间隔I、快慢车开行数量比π有关,即y(N,I,π)、n1(N,I,π)、Δn(N,I,π)。根据快车停站方案及以上参数确定越行站后,配线增加后不能更改,为尽可能检验和适应不同的开行方案,所以对三者的具体公式进行拟合,得出经验公式,以防止后面由于客流条件变化,开行方案变化后,越行站不适应的情况。所使用的数据为灵敏度分析结果见表2。 表2 越行站灵敏度分析结果 假设越行站控制性指标的设置规律的基本形式分别服从二次多项式方程,有a0+a1N+a2I+a3π+a4N·I+a5I·π+a6N·π+a7N2+a8I2+a9π2。使用最小二乘法对y(N,I,π)、n1(N,I,π)、Δn(N,I,π)分别进行拟合,有 y(N,I,π)=10.55-1.38·N+0.042 8·N2+ 0.022 5·I-0.001·N·I-5.65×10-6·I2+ 6.73·π+0.099 4·N·π-0.005 78·I·π- 4.404·π2 (12) n1(N,I,π)=-0.736+0.051 4·N-0.001 055·N2+ 0.013 5·I+2.31×10-5·N·I+ 1.67×10-5·I2+0.293·π-0.010 1·N·π+ 1.67×10-4·I·π-0.064 7·π2 (13) Δn(N,I,π)=36.99-1.577·N+0.014 6·N2- 0.002 9·I+1.28×10-4·N·I- 1.452×10-6·I2-28.62·π+0.638·N·π+ 0.001 06·I·π+8.30·π2 (14) 使用R2检验所提出的越行站设置规律方程的拟合程度见表3。 表3 越行站设置规律方程的拟合程度 根据所提出的规律方程,越行站数的拟合程度较好(R2>0.85)第1越行站和越行站间隔的拟合程度较优(R2>0.90)。说明所建立的规律方程可用于越行站设置的检验和校对。 本文分析总结了市域快速轨道交通组织快慢车运行的基本规则,针对快慢车是否发生越行及越行站设置位置分别建立了数学计算公式,并设计了基于规则的越行站位置设计算法。通过调整不同参数,发现越行站的设置规律,可总结为: (1)第1越行站n1的设置与快慢车开行数量比无关,也与区间通过能力无关;n1随着慢车与快车发车间隔时间Ile增加呈单调递增趋势。 (2)随着快车比例的上升,相邻两越行站间隔逐渐减小,并且在快车比例较小时变化较为明显,变化曲线类似于二次函数。因此,出现图中同一Ile情况下,n1值相同,而随着快车比例增加,越行站的布置越来越紧密的趋势。 (3)随着线路通过能力N的增大,相邻两个越行站之间的间隔越来越小,越行站位置还会受到快、慢车在各站停站时间的影响。因此,在规划越行站之前需要明确快慢车发车比例、列车停站方案以及最小停站时间的大小。 最后,使用多项式拟合方法总结越行站数y、第1越行站n1以及越行站间隔Δn的计算公式,为组织快慢车越行提供了较为全面的理论计算依据。结果表明本文提出的方法适用于实际轨道交通线路越行站位置计算,可以为线路设计及运营组织提供有效的理论支撑。1.2 越行站位置确定方法
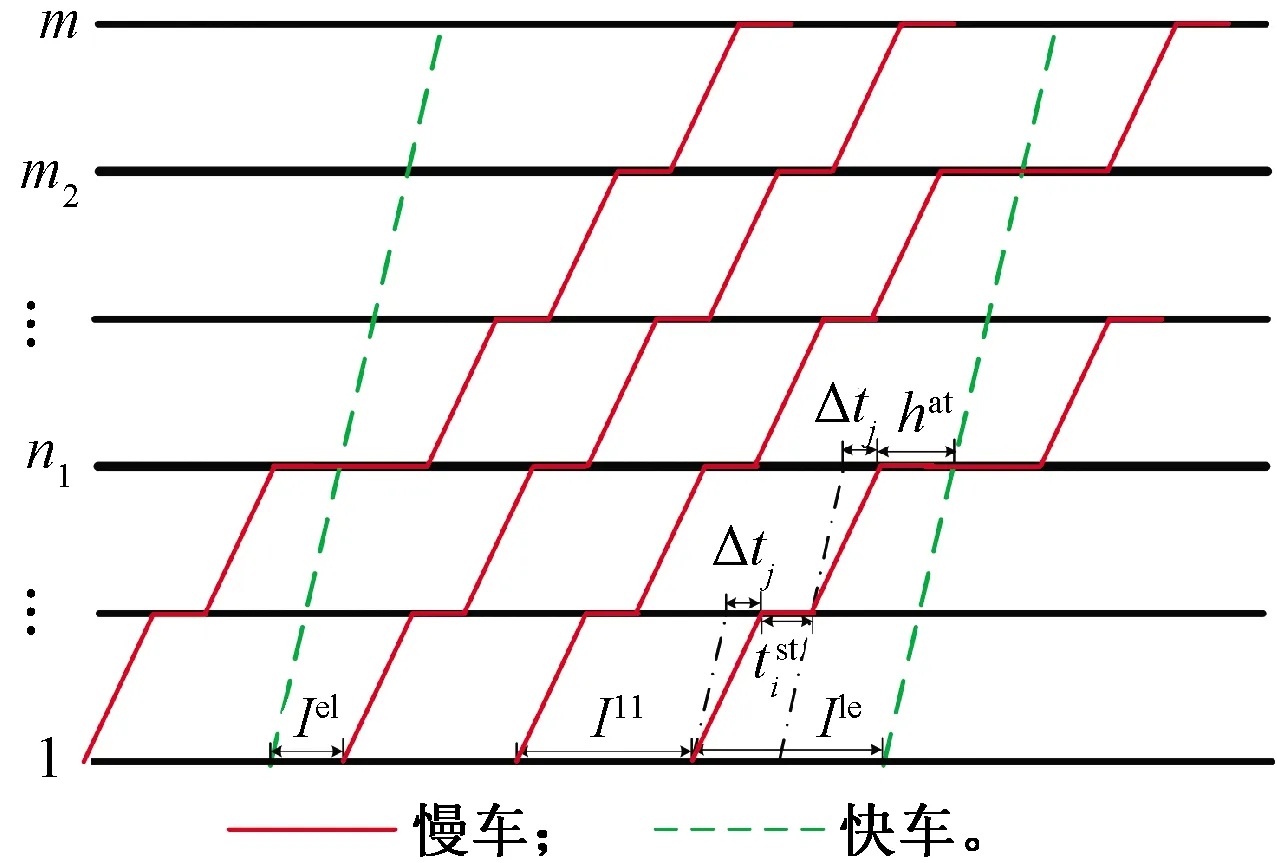
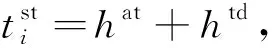
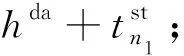
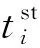
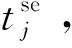
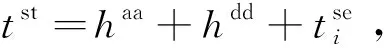
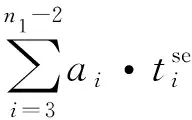
2 基于选择规则的越行站设置模型及启发式算法
2.1 越行站设置模型
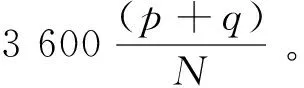
2.2 启发式算法设计
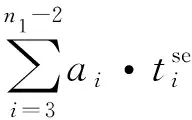
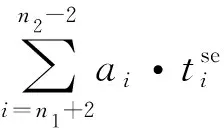
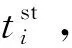
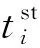
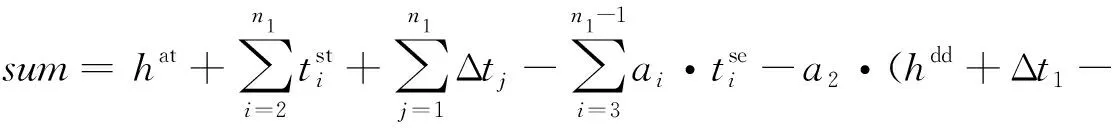
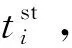
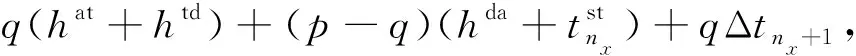
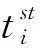
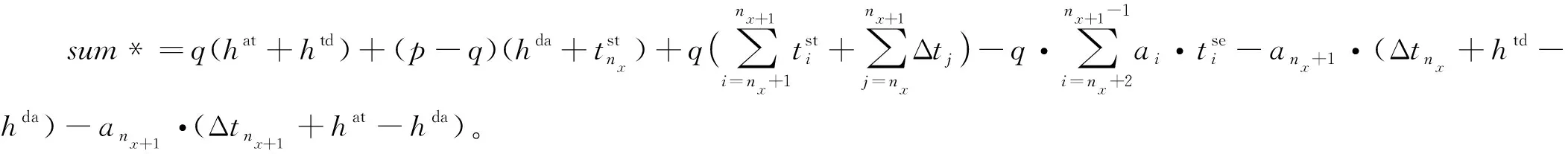
3 案例分析
3.1 案例设计与求解
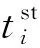
3.2 快车不停站与停站情况下越行站设置方案对比
3.3 越行站设置灵敏度分析
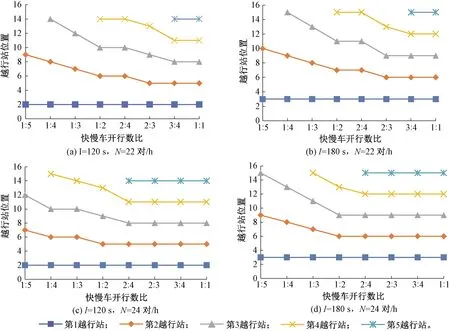
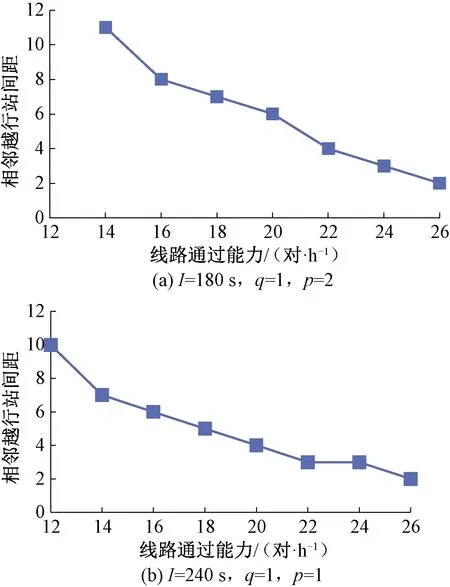
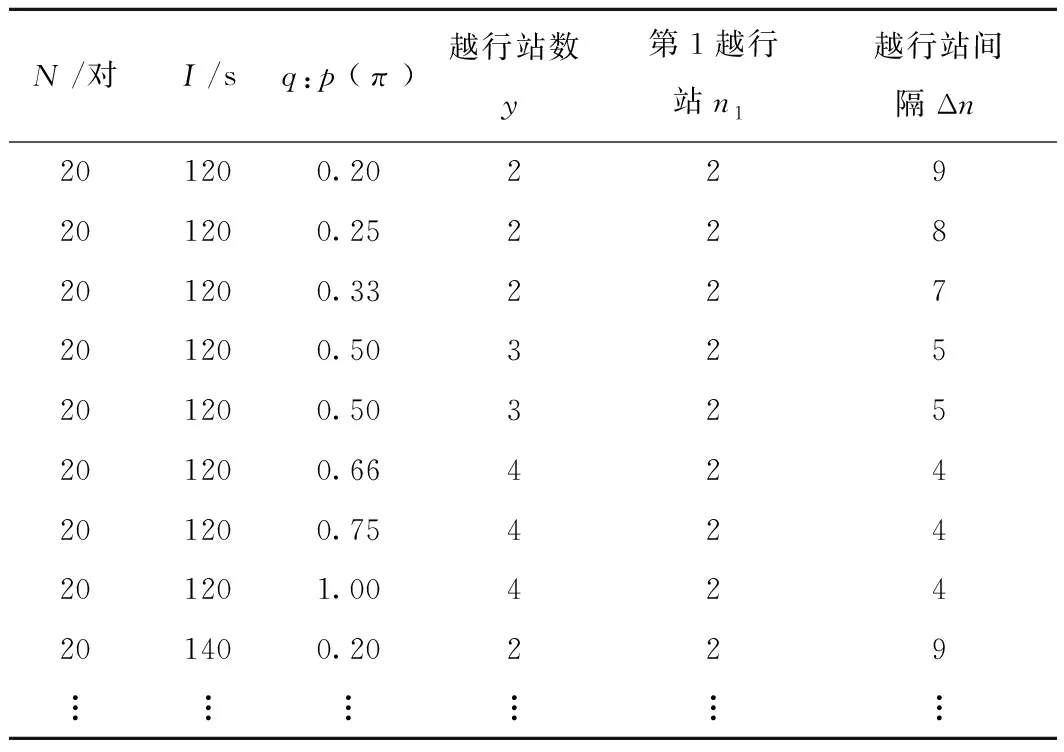
3.4 越行站设置定量公式研究

4 结论
