基于点融合的多跑道进场航班排序*

王 宁 翟文鹏

（中国民航大学空中交通管理学院 天津 300300）

0 引 言

点融合系统（point merge system，PMS）是基于性能导航技术与雷达管制相结合在空域和飞行程序方面的集成应用，主要用于解决进场交通流汇聚问题并优化间隔管理。相较于标准仪表进场程序的雷达引导过程，PMS的引入主要简化了管制员指挥调度的指令，然而进场效率的提升从根本上依然需要进场排序和调度的研究为管制员提供有效的航班序列作为支持，所以针对在PMS运行的基础上的航班进场排序与调度开展相关研究对于终端区空域效率有重要意义。

Liang等[1-3]率先针对PMS的进场航班排序展开相关研究，设计新的点融合程序，通过模拟退火算法和滑动时间窗对点融合进场过程进行排序以及4D航迹的优化。Hong等[4-5]提出了1种基于混合整数线性规划（MILP）的点融合排序算法以最小化飞行时间为目标优化着陆时间；后续针对航班下降期间的不确定性因素，提出带有鲁棒性解决不确定性规划的方法。You等[6]针对并行结构的PMS根据带有精英策略的遗传算法解决排序和调度问题。后续的关于PMS下的进场航班排序研究主要针对多个目标的动态求解问题，Hong[7-8]等针对PMS以最小延误和最小管制员负荷为目标利用蒙特卡洛分析和混合整数规划进行优化。Zhang等[9]以最小化总延误时间、最大总飞行时间和单航班的最大飞行时间为目标构建多目标模型进行航班进场的排序调度优化。张军峰等[9-10]针对进场多目标优化问题利用帝国竞争算法进行排序与调度优化。夏正洪等[11]利用雷达管制模拟机对点融合程序进行排序验证点融合程序相较于传统程序的有效性。关于进场航班排序的算法方面，包括模拟退火算法[12-13]、蚁群算法[14]、贪心算法[15-16]等。

标准进场程序的航班优化一方面从约束条件和目标入手，选择更先进的优化算法；另一方面对进场的航迹进行优化选择更为有效的下降航迹。PMS的应用适应于终端区空域范围广、容量大的大型国际机场，而且针对国空域划分的特殊性，点融合程序是与标准仪表进场程序混合同时运行导致航班的进场程序更为复杂。航班在进场时首先要考虑的是从哪条程序下降进近，其次才能确定排队序列和进场下降的航迹。而对于混合程序运行的终端区来说，还要同时考虑是否选择点融合程序，选择程序后才能考虑排队序列。针对结合PMS具有复杂进场程序的终端区，考虑通过将进场程序和跑道分配给进场航班并结合点融合程序优化进场排序来达到提高终端区进场运行效率的目的。

选取上海浦东机场进场程序，通过0-1整数规划将不同进场程序分配给航班，以最小总延误时间和最小总飞行时间为目标函数，建立多目标进场航班优化排序模型，并结合非支配排序遗传算法对模型进行求解，确定航班的落地序列和进场程序，并与实际运行结果对比分析，实现通过利用点融合程序缩小飞行时间和延误的目的。

1 点融合系统

点融合系统[17]的运行流程可概括为3个步骤：准备排序、建立排序、按序下降。如图1所示，准备排序：在航班进入排序边之前，管制员先检查确定航班序列、进入条件（高度/速度/间隔）并发布指令。可以通过自动化系统中图形工具（测距）或基于进场管理系统给出着陆次序。建立排序：航班沿排序边水平匀速飞行，管制员监控已排序航班之间的间隔。一旦排序边上的航班与前机达到间隔配备，发布“直飞”指令。排序下降：管制员在考虑平行于排序边上的下降航班之间的间隔配备后，下达下降指令，然后通过改变速度优化间隔并考虑退出系统。

图1 点融合进场程序图Fig.1 Procedure of point fusion approach

传统进场程序运行过程中，管制员是通过改变航班的航向和飞行速度来调整航班的安全间隔，也就导致了航班的飞行间隔主要依靠管制员的经验来调控。尤其在进场航班数量较多时，管制员很难判断如何调度航班来提高整体运行效率，调度的主要目标是使航班满足安全间隔安全着陆，也就导致航空航班的实际运行间隔要远远大于安全间隔，这也是产生航班延误的重要原因。引入PMS后，融合点代替了传统的起始进近点，排序边和下降到融合点的过程代替了进场过程。排序边上个点到航班的距离相同，所有管制员可以通过调整多架航班在排序边上的飞行时间来调整航班之间的间隔，航班在排序边排序下降的时刻差值就是航班之间的时间间隔。因为航班可以严格按照程序飞行，所以航班之间的时间间隔可以很大程度上的逼近最小安全间隔，达到减少航班延误的目的。

2 基于PMS的多跑道进场航班排序模型

考虑到进场程序在加入PMS后，航班的进场过程变得更为复杂。即是否选择PMS进场、是否在排序边上排序后进场。不同进场过程的飞行时间范围不同，航班选择不同的进场过程会导致不同的落地时间窗。所以考虑航班可选择的进场程序，根据选择不同的进场程序确定落地时间窗对航班进行优化排序，还可以通过PMS可以优化安全间隔的优点对航班的飞行时间进行优化。

2.1 PMS下多跑道进场航班排序方法

2.1.1 PMS下多跑道进场航班排序规则

航班在实际运行过1个进场程序过程依次要经过进场点、进场路径、起始进近点、中间进近点、最后进近点、接地点和跑道，而PMS的融合点一般设计在在标准仪表程序的起始进近点。由于航班在融合点的高度确定，航班在融合点汇聚，所以将融合点的序列作为航班着陆次序，即假设在起始进近点以前将航班的的次序和间隔调度好。

假设有2条独立平行进近跑道，每个航班的进场时刻，预计到达时刻，最早、最晚到达时刻和机型已知（见图2），先将进场航班根据进场时刻安排在1条跑道上，将其中时刻紧密的的航班分配到另1条跑道上，这样做的好处是能够在随机排序的过程中尽可能的将其中1条跑道的时隙资源充分利用将航班排的更加紧密以达到目标更优。再根据将进场程序随机分配给航班，根据进场程序、航班性能等确定航班的着陆时间窗，对各个航班进行排序确定着陆次序。

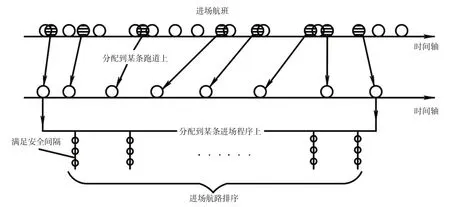
图2 PMS下多跑道进场航班排序规则Fig.2 Sequence rules of multi-runway approach flights under PMS

2.1.2 进场航班排序方法

假设机场有r条独立平行进近跑道，每个航班的进场时刻，预计到达时刻，最早、最晚到达时刻和机型已知。根据航班的进场点和进场时刻，考虑目标函数的要求下，将合适的进场程序的不同航路分配给航班，再将航班安排到第1条跑道上，根据航班在航路上的飞行时间，计算航班的落地时刻，若不满足安全间隔要求，将不满足的安排在第2条跑道上，若第2条跑道上的航班也不满足要求，则重新分配航路。

通过对实际运行的大量数据可以统计从不同航路进场的航班选择不同排序边即不同进场程序的飞行时间范围，据此为飞行时间约束，分析航班之间的最大调整量和最大调整飞行时间。也就是说航班选择何种进场程序进场影响整个终端区的运行情况。可以通过0-1整数规划来将某1个时间段的航班能够选择的进场程序进行合理分配，在满足约束的条件下将延误降到最低。也就是说，在实际运行过程中，通过即将到达终端区的航班的进场时刻，通过系统的计算可以提前分析出最佳的着陆次序并为管制员提供有效的管制指令建议。

2.2 点融合程序下多跑道进场航班排序模型建立

2.2.1 目标函数

1）总延误时间最小。航班的进场延误时间是综合机场、航空公司双方的效益诉求，即所有航班与预计到达时间的总和最小，即

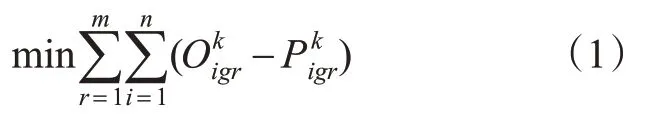
2）总飞行时间最小。由于航班选择不同进场程序的预计到达时间不同，在满足最小延误的基础上还要考虑到管制员管制时间和飞行员飞行时间的工作负荷需求，选择所有航班的飞行时间最小为另一个目标函数，即

2.2.2 约束条件

1）尾流间隔约束。关于连续的前后2架航班，由于航班在飞行时的机翼上下表面会产生由于压力差产生的涡流，航班向前运动则形成航班尾流，对后续的航班正常飞行造成影响。尾流的大小与前机的机型大小和重量有关，一般来说是成正相关。所以，航班的进场排序必须满足尾流间隔的约束。

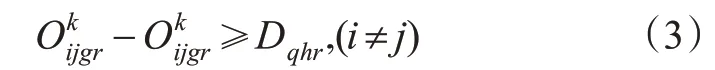
式中：Dqhr为前机机型为q后机机型为h且进场程序为r前后机的尾流安全间隔。由于PMS的进场过程，管制员可以在进入点融合程序之前可以调配安全间隔，然后根据优化后的序列通过点融合程序再进行排序调度，所以假设所有航班的落地次序与间隔为航班通过融合点的次序与间隔。

2）着陆时间窗约束。航班的着陆存在最晚和最早着陆时间[18]，最晚着陆时间主要根据航班的燃油消耗和燃油储备；最早着陆时间主要根据航班的飞行性能和选择的进场程序，即下降速度越快，航程越短，着陆越早。

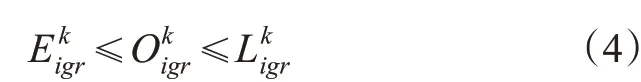
3）进场程序约束。航班从进场到着陆的整个过程只能选择1条进场程序（包括PMS）和跑道，不存在在运行过程中临时修改进场程序和跑道；由于实际运行中有些进场程序不存在交集，即从某一进场点g进场的航班只能选择所能可以经过的程序r，r的个数根据终端区实际进场飞行程序确定。设进场点为g的航班的可选进场程序集合为Rg。

2.2.3 基于0-1规划的PMS进场航班排序模型

假设航班在终端区的进场点为g。各个进场点在经过一段非等距的进场航路后会汇聚到多个汇聚点，也就是各个航班可能发生冲突的点，管制员需要提前对各个不同进场点进场的航班进行调度，可以通过安排到不同高度的高度层，或者到达汇聚点的时间不同来避免航班在汇聚点发生冲突。假设在确定进场时间的情况下对各个刚进场的航班1个最优化的着陆序列，管制员可以通过利用到达汇聚点的早晚来决定着陆次序。但是当航班进场较为密集的情况下，航班数量较多，管制员无法及时对各个航班进行到达前后时间的调度，还要通过不同高度层的分配。这就会导致实际排序与优化序列不同。引入点融合程序后，管制员可以仅通过发布航向指令就可以调度航班序列，省掉了高度层分配和调速指令。

在点融合程序的基础上，将点融合程序的排序弧分为λ个阶段，第λ阶段的起止时间为[(λ-1)θ,λθ]，θ为将点融合均分λ阶段的每一阶段的飞行时间。通过这种方式，可以确定从各个进场点进入的航班可选择的进场程序。图3表示从进场程序r进场的航班i可选择的进场程序与其他航班的机场程序进行优化排序，根据选择的程序、进场时刻在满足约束调价下得到航班的着陆次序。

图3 航班排序流程Fig.3 Flight sequencing process

设多个进场航路点共计m个进场程序，以0-1规划为基础，假设决策变量为Xikr，xikr=1为i分配程序r进场程序给k进场点进场的航班i。

约束式（7）～（8）表示1个航班仅且只能分配1个进场程序进场且所有航班不能在中途改变进场程序。

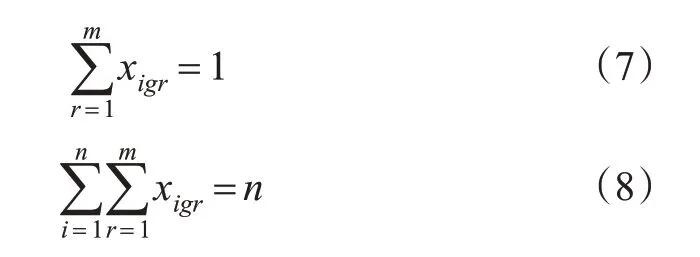
设某时间段进场航班有n架，以进场航班为行向量，进场程序为列向量，则航班i的其他程序为，航班i选择进场程序r的决策变量为=(0,…,1,…,0)（Xigr为1×r矩阵，1位于第r列），所经程序r的飞行时间为Fkr，据此可以得到进场航班和航班选择进场程序的0-1变量矩阵。

则所有航班的选择进场程序r的优化落地时间为

结合式（1）～（10），基于0-1规划的点融合多跑道进场航班排序模型的目标式为（1）和（2），约束条件式为（3）～（9）。

3 基于0-1规划的NSGA-II算法

进场航班的优化排序具有多目标多约束的特点，所以选取带有精英策略的快速非支配遗传算法（NSGA-Ⅱ）对模型进行求解。

考虑到模型的优化排序首先是对进场航班的进场程序进行随机分配，随机生成初始解的范围根据进场程序的个数随机生成，另外还要考虑到初始解生成后转化为0-1矩阵模型进行求解。其次在交叉变异的过程中，由于不同进场点的可选择的进场程序不同会产生不满足约束或者改变程序范围的情况，需要对交叉变异过程进行修改。所以针对以上考虑的情况，对NSGA-Ⅱ的算子重新定义，对交叉变异过程根据约束条件不同进行范围修订。

3.1 算法修改

3.1.1 基于0-1规划初始算子的生成

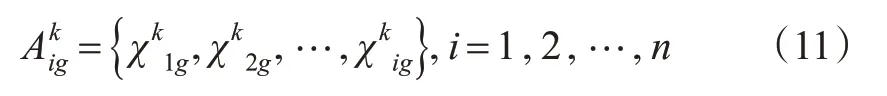
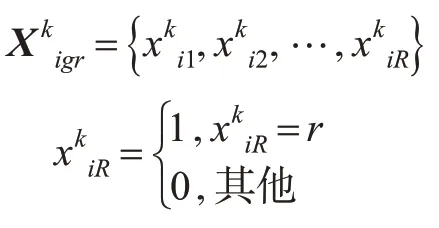
3.1.2 基于进场程序启发式交叉变异

为了避免某一进场点航班在交叉过程中产生的解导致该航班运行到另一进场点的进场程序中去，首先将各个进场航路点归类，对同一进场点的航班的染色体进行交叉变异操作，这样产生的新的解不会改变原来某一进场点航班运行的进场程序范围。

3.1.3 对不满足约束的解筛选修复

重新利用0-1规划模型对新的种群的每个个体（解）进行计算，求得各个解相应的优化落地时间集合。对每个个体依据落地时间进行由小到大排序，依次对各个航班的的落地时间相减，得到各个相邻航班的时间间隔。在求差过程中若某2架相邻航班的时间间隔不满足间隔约束条件，则计算后1架航班的最晚落地时间与与前1架航班的落地时间的间隔是否满足间隔约束。若满足，则后1架航班的优化落地时间改为前1架航班的落地时间加上时间间隔；若不满足，则认定此个体为残次品，重新对该个体进行交叉变异。

3.2 算法流程

基于上述修改，算法步骤如下。

步骤1。获得本场进场航班的进场时刻。

步骤2。根据各航班的进场点分配进场程序，并根据选择的进场程序得到预计到达时刻并分配跑道。循环N次得到N组数据。

步骤3。根据航班的进场程序生成第一代种群，个体数为N。

步骤4。对整群所有个体进行非支配排序，得到1组非支配解。对这1组解进行交叉变异生成新的子代，将上1组非支配解和子代合并，再进行1次非支配排序，根据拥挤度计算规则计算个体拥挤度，将优良个体作为新的父代。

步骤5。对新的父代交叉变异产生新的子代返回步骤4循环，直至循环至最大迭代次数。最后输出结果。

算法流程图见图4。

图4 算法流程Fig.4 Algorithm flow

4 实例分析

4.1 仿真场景构建

选取上海浦东机场进场向南运行为例，根据17R和16L2条独立平行进近跑道的运行情况，对某天高峰时段01：35—02：35（方便计算，时间换算为秒，以00：00为0计算）的38个进场航班进行优化排序。浦东机场的进场程序见图5。SANAN进场点的航班有2条进场程序的航迹；BK进场点的航班可以左转通过BK-83A标准仪表进场程序进场着陆或通过BK-81A、BK-82A点融合程序进场；AND进场点的航班进场过程与经过BK的相同；DUMET进场点的航班有2条点融合进场程序航迹和1条连续下降运行（continuous descent operations）的进场程序航迹；MATUN进场点的航班有2条进场程序航迹。在这里将程序依次从1～13编号，点融合程序总数共计6条，程序编号分别为6、7、8、9、10、12、13，4个进场点中有3个进场点可以选择通过PMS进行优化排序。由于PMS上航班飞行高度层和飞行速度不变，航班的飞行轨迹一定，可以精确让实际间隔逼近安全间隔，所以通过PMS排序的航班的安全间隔设为最小安全间隔，最小安全间隔以文献[19]为标准，并做简单化处理，即前机机型为轻型机，与后机的时间间隔为90 s，前机为中型机，与后机间隔100 s，前机为重型机，与后机间隔为115 s。不通过PMS的间隔设为最小安全间隔的1.2倍。

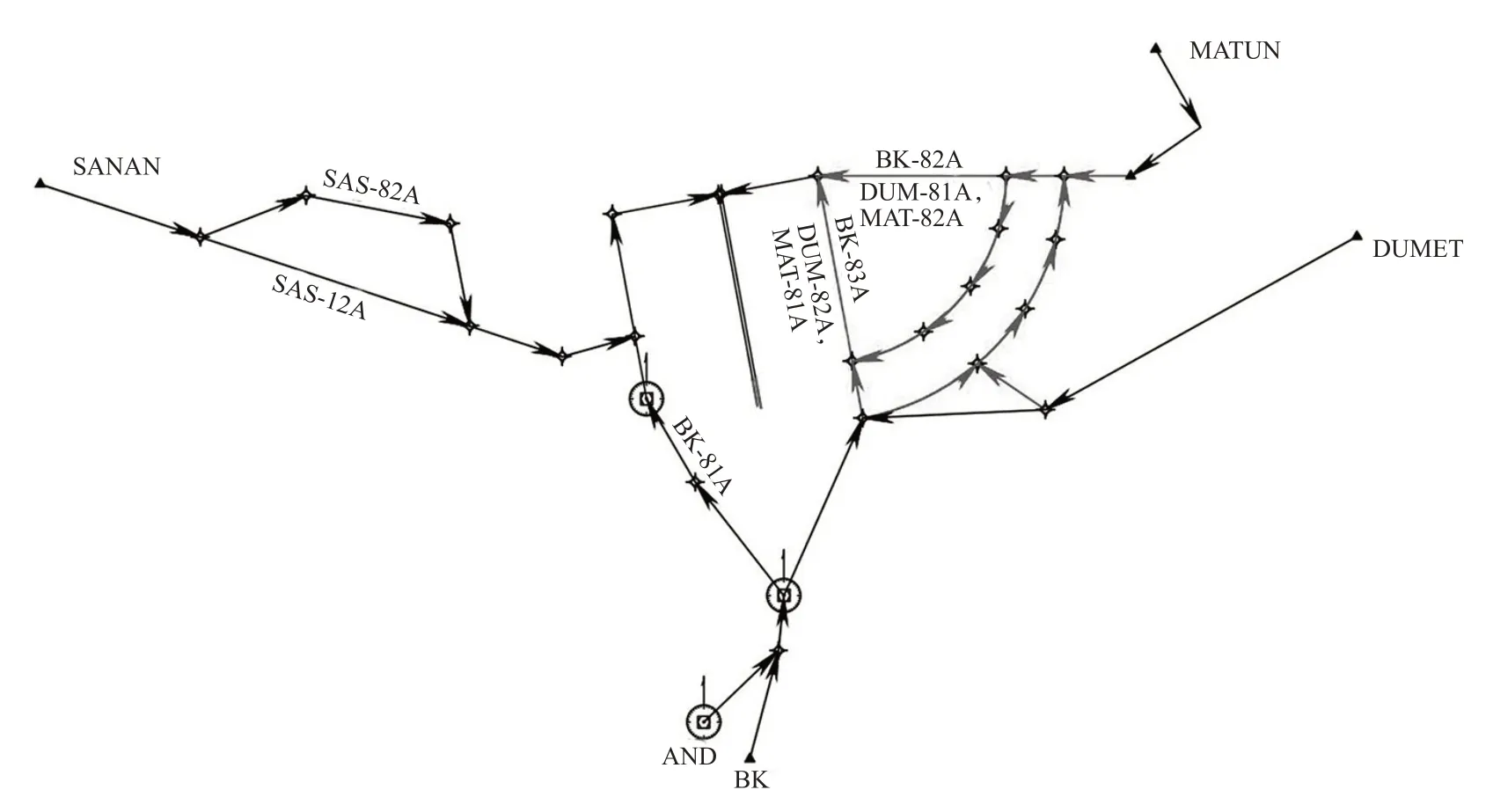
图5 浦东进场程序图Fig.5 Standard approach procedure of PudongAirport

统计浦东机场1 d的航班进场时刻、进场程序以及到达时刻，得到不同进场程序航班飞行时间的四分位数。如表1所示，航空的最早、预计、最晚着陆时间分别为代表不同航班选择不同进场程序对应的百分比进场飞行时间。

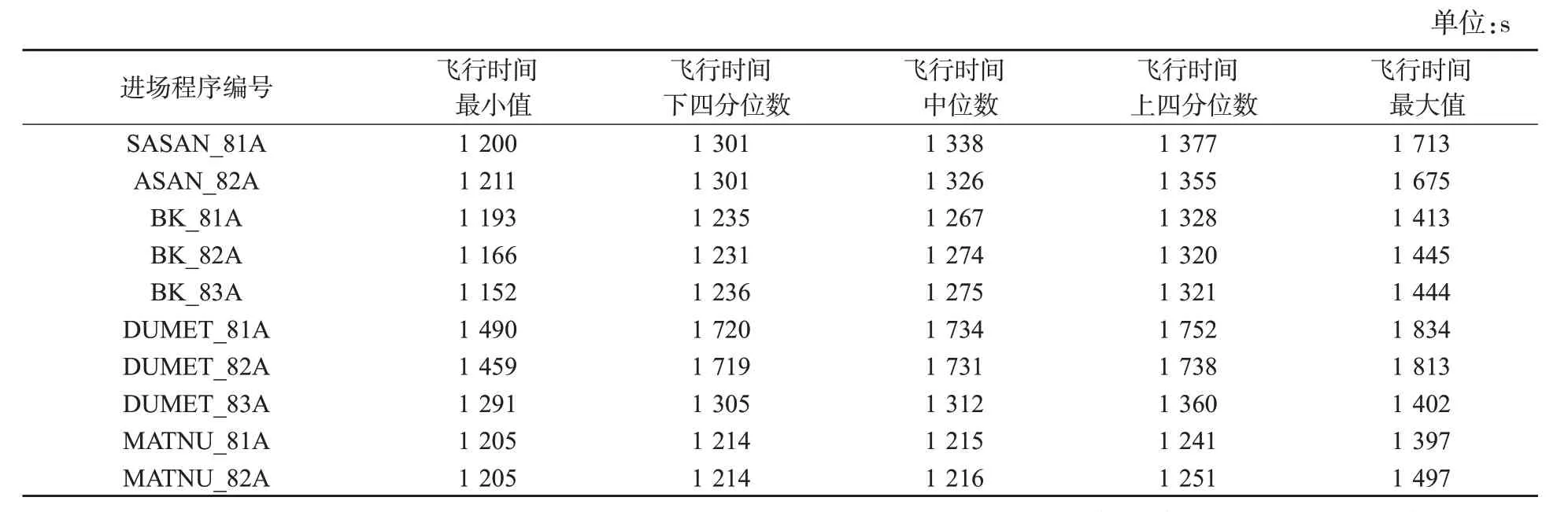
表1 各程序进场飞行时间Tab.1 Approach flight time of each procedure

4.2 优化结果分析

基于软件Matlab2017b，设置种群规模设为50，交叉、变异概率设为0.8和0.03，迭代次数200次。

由表2可知，通过优化后得到的结果明显好于实际的结果。经计算，优化后总飞行时间为49 582 s，相较于实际的总飞行时间52 149 s降低了5%，；优化后总延误时间1 774 s，比实际延误时间2 872 s降低了38.2%。可以看出，总飞行时间的降低也就是终端区的运行效率和容量提高了2.1%，延误时间降低了38.2%是由于优化后的进场航班通过点融合程序排序边调整安全间隔来逼近最小时间安全间隔，然后最大化的使航班进场飞行的时间最短，来达到延误的最小化。

表2 优化排序结果Tab.2 Optimized sorting results

统计基于0-1整数规划的NSGA-II优化和实际过程中的所有航班的着陆时间结果见图6，优化后大部分航班整体的着陆时间都要早于实际式着陆的航班。实际运行过程中，管制员对航班的前后间隔主要考虑安全性，且不考虑根据排序序列优化进场航班来减少不必要的延误。而优化过程通过0-1整数规划模型，在确定落地序列之后通过程序分配和PMS优化了前后航班的安全间隔，使得航班的着陆时间分配更加均匀、合理，从而达到减少航班延误、提高终端区运行效率的目的。

图6 优化结果图Fig.6 Optimized results

图7～8是各条跑道的优化结果和实际结果对比，结果得出优化后跑道1着陆的航班提高到25架，相较于实际航班的基础上提高了7架，证明延误时间和飞行时间的目标都得到了优化，跑道时隙资源被充分利用，跑道容量大大增加。因为研究对象是静态进场航班，选取的基础数据是1 h内实际的进场航班，跑道2的航班数相应减少了7架，使得跑道的流量压力大大减少，为跑道容量的提高提供了支持。

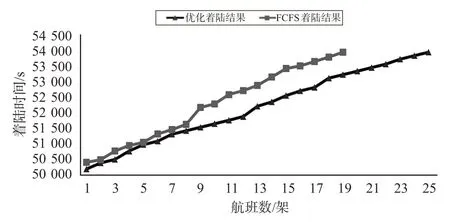
图7 跑道1着陆结果图Fig.7 Landing results of runway 1

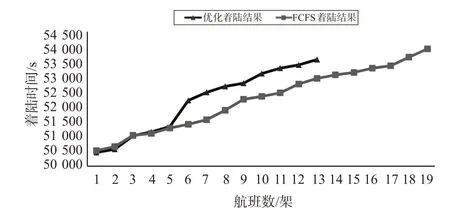
图8 跑道2着陆结果图Fig.8 Landing result of runway 2

与其他的进场排序方式相比，由于点融合程序下的进场程序为航班的进场下降提供了多种程序引导，通过0-1整数规划利用分配进场程序对航班进行排序的方式主要依靠将进场航班分配到不同进场程序，可以使航班的进场航迹不同来避免航班之间的冲突，来达到充分利用有限的空域和时隙资源提高运行效率的目的。通过分配不同的进场程序对航班进行排序，一方面解决了进场程序在引入点融合程序的情况下，航班应该通过何种程序进场下降来提高进场效率的问题；另一方面可以为管制员提供各个航班的既定进场程序和序列的决策建议。

5 结束语

论文针对最新引入的PMS，通过分析PMS优化飞行时间和安全间隔的特点以及、PMS下复杂的终端区进场程序中航班进场后能够选择的进场程序（各个标准程序或点融合程序），为航班选择有效的进场程序，再通过优化排序提高航班的进场效率。

1）分析点融合程序下，管制员发布指令调度航班排序着陆的运行过程，考虑航班准点率和终端区运行效率确定最小延误时间和最小飞行时间的目标函数。考虑到所选进场程序不同引起的飞行时间不同，并结合PMS优化安全间隔的特点，将不同进场程序和跑道分配不同航班确定航班落地时间。以此建立基于0-1整数规划的双跑道进场航班排序模型。

2）根据多个目标函数的线性规划模型，选取非支配遗传算法进行迭代求解，并将0-1整数规划的0、1变量解转换成适合优化算法迭代的常数变量解，设计基于0-1整数规划的排序算法。

3）选取上海浦东机场进行实例仿真计算，与实际排序结果对比，证明了优化后的排序结果能够有效减少进场航班的飞行时间和延误时间，且优化后的着陆航班的着陆时间间隔更合理、均匀，对提高机场的延误率和运行效率有重要作用。

由于论文是针对点融合程序和标准进场程序混合运行的具有复杂进场结构的终端区的进场航班，对进场程序和航班序列优化，只与先到先服务的实际结果进行对比分析，且未考虑航班在点融合程序中详细的四维航迹。未来在结合四维航迹、其他排序模型和优化算法等情况值得更深入的研究。