基于小波变换的电力营配系统暂态稳定性智能分析方法

2022-01-08王登峰陈银江张军喜雷鹏举李学斌

电子设计工程 2022年1期

王登峰，陈银江，张军喜，雷鹏举，李学斌

（1.国网宁夏电力有限公司，宁夏银川 750001；2.北京中电普华信息技术有限公司，北京 100085）

电力营配系统的主要任务是处理电力营销过程中出现的故障、营销权限等一些具有争议性的问题，提高电力企业的营销效果以及应用效果[1-2]。系统在运行过程中容易出现错误，因此电力营配系统暂态稳定性尤为重要，一旦系统失去暂态稳定性，那么电力营配系统将不具有任何意义[3]。

传统的电力营配系统暂态稳定性智能分析方法只对电力营配系统的暂态特征进行一次提取，导致电力营配系统暂态特征的有效性降低了，使电力营配系统暂态稳定性智能分析结果出现偏差，极易出现无法挽回的损失[4]。

该文基于电力营配系统暂态稳定性的原理，对电力营配系统暂态进行两次特征提取，并构建系统暂态稳定性评估模型，保证电力营配系统暂态稳定性智能分析结果的准确性。

1 暂态稳定性智能评估分析

1.1 分折电力营配系统暂态稳定规律

电力营配系统的稳定性是平衡电力各种发电机的输入机械转矩和输出电磁转矩之间的稳定性，保证电力设备按照一定的转速进行工作，促使电力系统稳定运行，如果电力设备的转速或者其他参数发生微小变化，就会导致电力营配系统的暂态稳定性出现波动，一旦波动持续，电力营配系统会失去稳定性，产生周期性混乱[5]。电力营配系统暂态稳定规律如图1 所示。

图1 电力营配系统暂态稳定规律

电力运行与配电系统暂态稳定原理的实质是电力运行与配电系统的运行特性，主要表现为摆动曲线形式。当电力运行和配电系统处于暂态稳定状态时，摆动曲线将根据电力设备的转速和功角形成周期性的摆动曲线，即当系统处于非暂态稳定状态时，电力设备的摆度曲线为非周期曲线[6-7]。电力营配系统暂态不稳定轨迹如图2 所示。

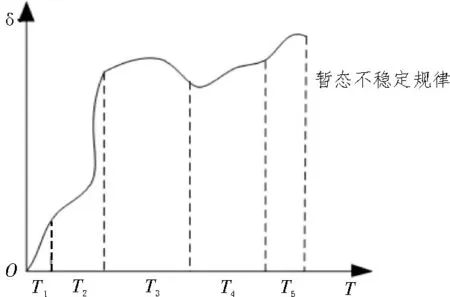
图2 电力营配系统暂态不稳定轨迹

电力设备在运行过程中，原动机对轴系施加机械转矩，使发电机产生电磁转矩，当受到外界干扰后，若机械转矩大于电磁转矩，则存在加速转矩。在设备加速转矩形成的同时，会出现设备间的摩擦力、空气阻力、摩擦损耗，进而加快或者降低设备的运转速度，所以根据机械质量守恒原理，综合设备运行影响因素，设计电力营配系统设备的净加速转矩计算公式，如下所示：

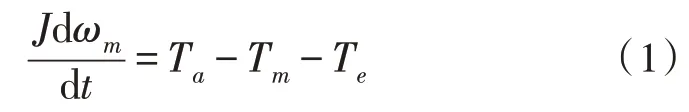
其中，Tm表示原动机对轴系施加机械转矩；Te表示电磁转矩；J表示设备转子惯量；Ta表示设备加速度；ωm表示发电机转子的机械角速度[8]。

电力营配系统的功角对系统暂态稳定性起到一个约束的作用，当功角的数值在摇摆曲线的极值处，则表示电力系统内部处于一个暂态稳定性的状态，但是一旦功角处于摇摆曲线的其他位置，则系统处于暂态稳定性失衡的状态。功角的有效范围为0°～180°，功角为90°时系统处于最佳暂态稳定性，电力营配系统的功角趋近于90°表示系统的暂态稳定性平稳，趋近于0°表示系统的暂态稳定性失衡于电力系统机械功率，当功角趋近于180°时，代表系统暂态稳定性失衡于电力功效。具体功角的计算公式如下所示：

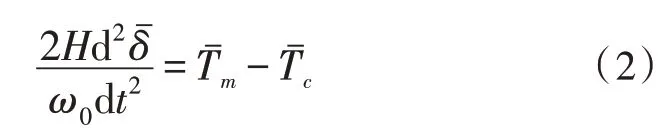
其中，H表示惯用时间常数；ω0表示转子角速度；表示相对于同步旋转坐标系的转子角位移；表示设备平均机械转矩；表示平均电磁转矩。

综合对电力营配系统加速转矩的转速和功角计算分析，最终摇摆曲线的规律公式如下所示：

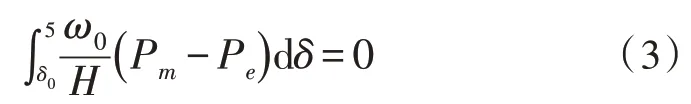
其中，Pm表示电力营配系统总输出功率；Pe表示电力营配系统有效功率；其他参数与上文意义相同[9-10]。

1.2 构建智能评估模型

该文通过支持向量特征方法完成电力营配系统暂态稳定性特征的提取，提取过程如下：

在电力营配系统的所有特征中随机提取一个特征输入，训练出一个特征向量形式，然后将此特征在电力系统特征序列表中清除，则支持向量额特征的的权向量将发生变化，根据电力系统参数的变化大小确定相应特征的重要程度[11-12]。将各个全变量进行递归处理，每个周期去除一个多余的特征向量，以此得出剩余的特征向量，再重复此操作，计算出其他的特征向量，最终得到系统暂态稳定性特征的排序列表。

根据支持向量特征提取原理，得出的提取目标函数如下所示：

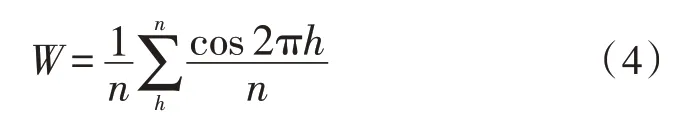
其中，n表示系统特征个数；h表示信号频谱幅值。

综合电力营配系统暂态稳定性目标特征函数和评估错分率，归纳出最终的状态评估模型如下所示：

其中，α表示正确的分辨率；k表示kappa 的统计值；u表示特征向量所表示积分的面积；∈1、∈2表示错分率。

根据以上评估模型可得出4 种电力暂态稳定性状态结果，如表1 所示。

表1 暂态稳定性状态结果

既然是评估模型就一定存在评估正确和错误两种结果，所以该文为了提高评估模型的准确率，在特征目标函数的基础上增加一个错分率叠加判断。错分率是评估结果的一个界限，并且该文采用两次评估的共同结果作为最终的评估结果，它可以有效地避免评估模型在评估过程中出现误差情况的发生。文中设计的错分率有两种类型，第一类错误概率是初次评估电力营配系统暂态为稳定性，而第二次评估电力营配系统暂态为非稳定性[13-14]。第二类错误概率是初次评估电力营配系统暂态为非稳定性，而第二次评估电力营配系统暂态为稳定性，具体表现公式如下所示：

其中，p(x|ω1)表示第一类样本分布概率密度函数；p(x|ω2)表示第二类样本分布概率密度函数。

2 暂态稳定性智能分析方法

2.1 小波变换算法分析

小波变换算法也被称为CWT，物理学家根据小波变换理论和函数可以自由平移和伸缩的特点，将小波函数根据实际情况进行不同尺度的信号变换，变换计算公式如下所示：

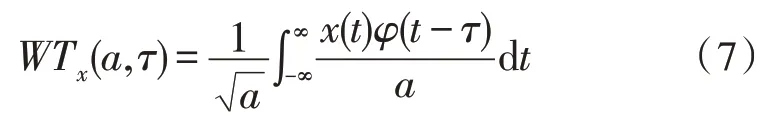
其中，a表示函数的不同尺度；φ表示函数的极值；τ表示函数移动位移的长度；x（t）表示小波变换函数的待分析信号。

小波变换函数的对应频域函数公式如下所示：

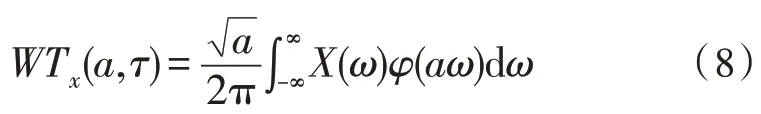
其中，X（ω）表示小波变换后傅里叶函数；ω表示函数的相位。

小波变换算法的应用要满足一定的函数条件，小波变换函数面向的对象无论是什么，变换函数尺度越小表示信号变化过程中的冗余信息量越小，变换效率越高，对应函数的变化频域范围越大[15]。

2.2 智能分析流程

根据小波变换算法和电力营配系统暂态稳定性原理以及电力营配系统暂态稳定性智能评估模型，该文总结出完整的基于小波变换的电力营配系统暂态稳定性智能分析方法流程，具体过程如图3 所示。

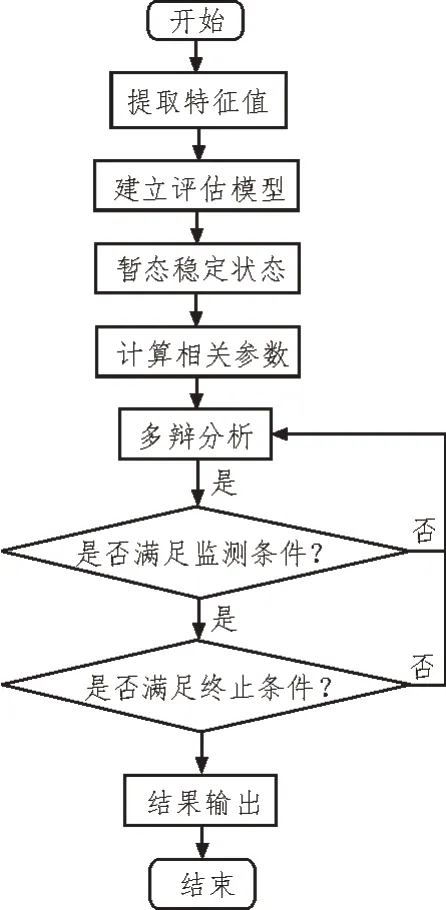
图3 基于小波变换的电力营配系统暂态稳定性智能分析流程

1）对需要分析的电力营配系统通过支持向量特征方法提取特征值，将提取的特征列表带入文中构建的电力营配系统暂态稳定性评估模型中，评估电力营配系统所处的暂态稳定状态；

2）根据实际情况采集电力营配系统的模拟信号以及离散数字信号，计算出小波变换函数谐波的振幅、相位等相关参数，构建小波变换函数；

3）根据小波变换函数完成电力营配系统信号的智能分析，分解出信号的频带和基波分量，利用小波变换函数和系统暂态评估模型完成电力营配系统暂态稳定性的评估[16]。

3 实验分析

通过以上分析，完成基于小波变换的电力营配系统暂态稳定性智能分析方法的研究，为了检验此分析方法是否具有意义，该文进行了对比实验完成验证，文中采用的对比实验是基于多属性决策树的电网暂态稳定规则提取方法（传统方法），共同完成实验分析。

为了保证实验的公正性和科学性，该文将对同一个数据库中的两个电力运行和配电系统同时进行相同情况下的暂态稳定分析实验。用两台计算机将新的分析方法输入到每台计算机的数据库中。工作人员将提前检查两种分析方法的运行环境，以防止实验过程中的事故和影响，实验结果如图4 所示。由于人工记录的数据会有一定的误差，该文通过两种分析方法连接的计算机，记录和监控了智能化电力运行和配电系统暂态稳定分析方法的分析过程。测试结束后，自动汇总测试的相关数据，如分析时间、分析准确度等，评价结果以表格的形式呈现。

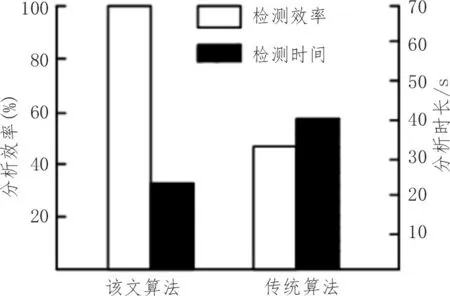
图4 分析时长实验结果

分析结果实验误差如表2 所示。

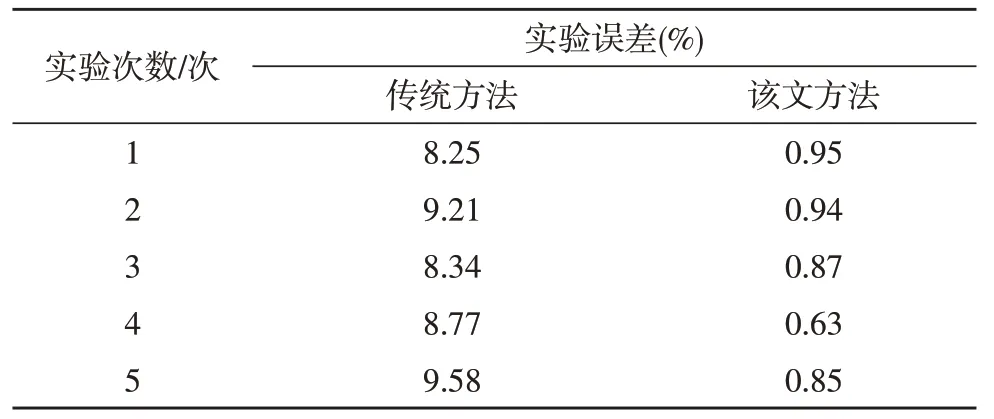
表2 分析结果实验误差

实验结果表明，两个分析方法都提交分析结果为指令，结束实验，开始清算实验数据，最终得出的实验结果是基于小波变换的电力营配系统暂态稳定性智能分析方法比传统的基于多属性决策树的电网暂态稳定规则提取方法用时短，并且分析结果准确性高。

该文在实验前，最大限度地排除了影响实验的干扰因素，使实验结果具有一定的意义。总体而言，基于小波变换的智能暂态稳定分析方法的各个过程具有很强的相关性，提高了分析方法的效率。产生这种结果的主要原因是在传统分析方法的过程中，该文加入了一种智能化的电力运行与配电系统暂态稳定评估模型，将特征选择法和权向量算法相结合，完成了电力运行与配电系统暂态稳定的初始特征评估，为电力系统暂态稳定的智能分析方法提供了准确的分析数据。此外，该文还利用小波变换算法建立了配电系统暂态稳定评估模型的混淆矩阵。如果在评估中存在误差，通过该过程可以检测出误差，提高了配电系统暂态稳定智能分析结果的准确性。综上所述，基于小波变换的智能暂态稳定分析算法意义重大，分析结果准确有效。