基于神经网络的电厂磨煤机运行状态智能分析技术

宿星会，张宝国，吴家伟，韩建刚，闫超

（华电国际十里泉发电厂，山东枣庄 277103）

近年来风力发电、太阳能发电等新能源发电技术的发展速度较快，应用前景也较为广阔。但火力发电作为我国目前的主要发电方式，目前仍占据着全国总发电量的70%以上[1]。发电厂中的设备产生故障将会中断正常供电，损害社会经济效益。因此，对火力发电厂设备的运行状态进行检测和分析，是保证电网稳定、可靠运行的必要条件，也是电网技术改革的进一步目标[2]。

磨煤机作为电厂辅机，是发电系统的重点监测对象之一。目前对于设备的状态预测分析方法主要分为三类，即基于数学模型、基于信息处理和基于知识的方法。文献[3]在电力设备状态分析中，使用了振动诊断法。但这种方法只适用于设备在故障已发生且故障状态较为明显的情况，并不能起到状态预测的作用；文献[4]将证据理论用于电子设备状态分析，但该方法不能较好地处理两个证据冲突时的情况，从而导致预测结果的可信度不高。而神经网络在具有迅速寻求最优解能力的同时，还能够根据历史情况对数据的未来发展趋势作出准确预测。鉴于神经网络具有以上优势，该文将其应用于电厂磨煤机运行状态分析领域。

1 磨煤机常见故障分析

研究对象选取的是由长春发电设备总厂生产的MPS225HP-II 型中速磨煤机。该机组主要由基础电机、齿轮减速机、动态分离器、磨盘、液压系统、送风及密封系统、磨辊等部分组成。

1.1 主要监测参数

1）磨出口温度。其是指一次风口处输出物的温度，是表示磨煤机干燥性能的一个特征参数。

2）磨煤机电流与排粉机电流[5]。这两个电流的大小决定了输出功率的大小，是表示磨出力情况的一个特征参数。

1.2 常见故障分析

在实际的复杂运行条件下，导致磨煤机发生故障的原因众多。文献[6]中分析了磨煤机可能出现的常见故障，并结合某发电厂的磨煤机机组的大量实际数据对各种故障出现的概率进行统计，如表1 所示。

表1 不同故障发生次数及概率

从表1 中可以看到，煤量异常和磨出口温度过高这两类故障发生次数超过了总故障次数的70%。因此着重对这两种故障进行分析，并从中确定典型的运行特征参数以建立神经网络模型。

1）煤量异常[7]。发生煤量异常的情况有两类：煤堵塞、少煤或断煤，故障主要由风量不足或传送装置故障导致。当少煤或断煤时，磨煤机电流相应减小；机器内部出现轻微煤堵塞时，磨煤机电流会相应增大；但当堵塞程度继续增大至磨煤机不能工作时，磨煤机电流将会减小到0。因此，磨煤机电流变化足以实现对磨煤机运行状态的准确分析[8]。

2）磨出口温度过高[9]。引起磨出口温度过高的原因有一次热风口开度过大、煤的初始湿度过低等。磨出口温度过高可能造成煤粉堵塞，进而引起煤粉自燃或爆炸。因此将磨出口温度作为监测变量来评估和预测系统的运行状态，对于磨煤机的安全、稳定运行是必要的。

2 基于神经网络的状态分析方法

2.1 BP神经网络原理

考虑到神经网络在处理数据时具有强大的自学习能力，能够通过对历史数据的分析达到对数据未来的发展趋势作出预测，因此适合处理状态分析这种复杂非线性系统中的预测问题[10]。故在该节中，将从能够反映上述两种常见故障的典型运行特征参数出发，搭建单个特征参数的神经网络预测模型。

在目前种类繁多的神经网络中，当属BP（Back Propagation）神经网络应用最为广泛，其尤其适用于智能故障诊断方面[11]。在结构上，BP 神经网络的结构如图1 所示。其包括输入层、隐藏层和输出层，每一层均包含若干个神经元。神经元之间的连接代表着权值系数，权值系数是根据网络的调整而不断变化的。BP 神经网络的本质思想是比较正向传播过程计算得到的输出与期望值之间的误差。在不满足误差条件时，转向反向传播过程。将误差逐层逆向传播，从而不断调节各节点的权值系数。通过多次迭代，不断调整权值系数使输出的误差最小，得到相应的模型，即完成了模型的训练。

图1 BP神经网络结构示意图

2.2 BP神经网络模型构建

2.2.1 算法设计

最基础的BP 算法在实际应用中存在易于陷入局部极小值、收敛速度不够快等缺点，从而导致网络的泛化能力不足。因此该文采用LM（Levenberg-Marquardt）算法[12]对BP 算法进行优化，具体算法步骤包括：

1）初始化。将网络中的权值系数、阈值及最大误差允许量ε赋予初始值。

2）正向计算。利用已设条件计算网络的输出误差E，当E＜ε时，学习计算结束。

3）反向计算。若计算误差大于ε，则需进行反向误差传播计算。通过LM_BP 算法计算网络的局域误差、梯度和海塞矩阵确定搜索方向，进而修正网络参数并返回执行正向计算，直至输出满足误差要求。算法流程如图2 所示。

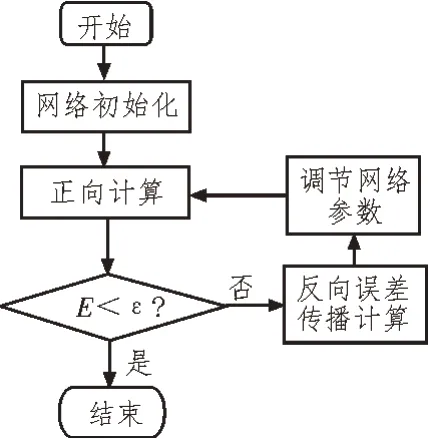
图2 LM_BP算法计算流程示意图

2.2.2 数据处理与网络结构

1）样本选取。该文将根据时间序列预测理论[13]，使选取的数据之间的相关性更强，实现更准确的状态预测。时间序列预测理论的基本原理是根据过去所获得的数个样本点拟合出下一时刻的数据值。再将预测值作为已知量用于下一点的拟合中，从而实现状态的连续预测。所选取的样本点数过少会造成部分特征丢失，而选取的样本点数过多则会引入更多的噪声，这两种情况均使模型的预测精度降低。文中以磨出口温度预测为例，将输入数据长度分别设为5、10、15、20点。其均方根误差情况如图3所示。

图3 输入数据长度对预测结果的影响

由图3 可知，在输入数据长度为10 点时，均方根误差最小，效果最为理想。因此，可以将样本数据按表2 所示划分。

表2 训练样本选取

2）归一化处理。选取样本后，对样本进行恰当的数据预处理将成为网络训练效果是否能达到预期的关键。考虑到在神经网络中隐藏层与输入层的传递函数将使用Sigmod 函数[14-15]，因此要将样本进行归一化处理。采用Matlab 工具箱中的Mapminmax 函数进行处理，其函数式可以表示为[Y,PS]=Mapminmax（X,0,1）。其中，X、Y分别为归一化前后的数据；PS 为包含原数据峰值、谷值等特征信息的数据结构体，可以用于数据的归一化与逆归一化。

3）网络节点数的选取。由于输入数据长度为10，故输入层的节点数选为10 个；仅需预测下一个点的数据，故输出层的节点数选为1 个；隐藏层的节点个数可以由式（1）和式（2）计算得到：

式中，m为输入层节点数，n为输出层节点数，α为1～10 内的常数，i为所求隐藏层节点数。综合考虑式（1）和式（2）后，可求得模型中隐藏层节点数为4。因此，文中所构建的BP 神经网络为10-4-1结构的三层网络。最终在Matlab 中以Tansig 函数作为网络传递函数；以Learngd 函数作为学习函数；以Trainlm 函数作为训练函数，完成BP 神经网络的构建。

2.2.3 模型训练

构建完成BP 神经网络的预测模型后，为进一步提高网络的泛化能力，需要通过训练样本对网络进行训练，从而调整网络中的权值系数来优化网络模型以达到减小预测误差的目的。神经网络中的各参数设置如下：学习率Lr=0.01，最大迭代次数Epochs=100，训练要求精度ε=0.001，动量因子Mc=0.9。网络的训练结果如图4 所示。

由图4 可知，神经网络训练的均方根误差结果在第60 次迭代后就趋于稳定，且其误差能够满足要求。

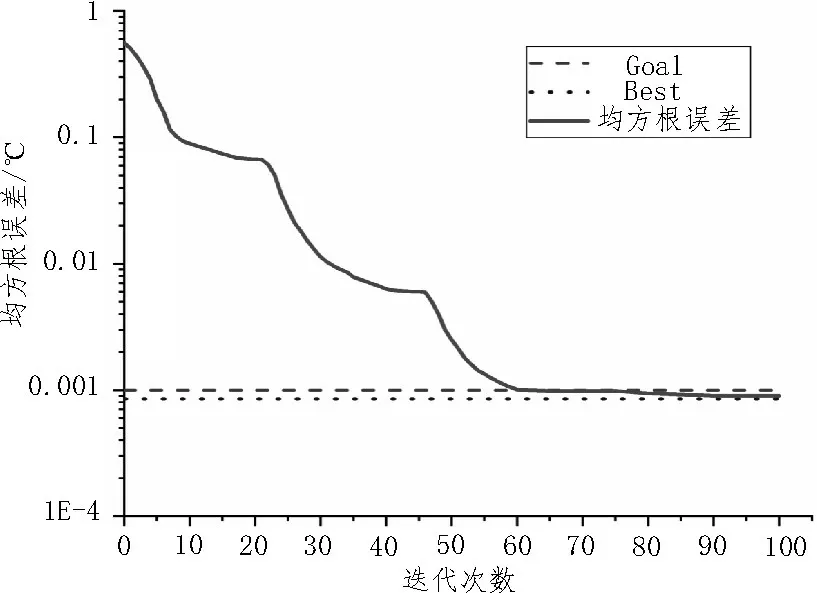
图4 神经网络训练均方根误差图

3 不同状态下的模型预测及分析

3.1 磨出口温度预测

在磨煤机正常运行的情况下，对其进行磨出口温度预测。在100 min 的测量时间内，共采集50 个数据点信息。将其中25 个数据按照2.2.2 节中所述的方法进行处理，并将其作为训练样本输入。通过磨出口温度预测的神经网络训练结果如图5 所示。另外，25 个数据点构成的曲线代表在测量过程中得到的实际值。可以看到，预测值与实测值的变化趋势是相同的。

图5 磨出口温度预测结果

3.2 磨出口温度预测模型误差分析

利用均方根误差法[16]对预测模型的准确度进行分析。均方根误差（RMSE）的计算方法如下：

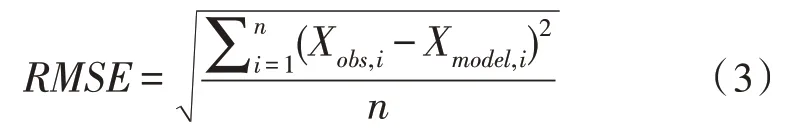
式中，Xobs,i为第i个点的实测值，Xmodel,i为第i个点的预测值，n为测点数量。计算可得，磨出口温度预测模型的预测值与实测值的均方根误差RMSE（T）=0.23 ℃。测量值的平均温度Xobs,av=95.12 ℃，根据均方根误差率的计算方法：

可以得到，磨出口温度预测模型的均方根误差率γ（T）=0.24%。因此基于该文提出的状态分析方法所建立的神经网络模型，可以准确地预测正常工作情况下的磨出口温度的状态变化。

3.3 煤量异常预测

上述磨出口温度预测模型所用数据样本是在正常工况下得到的，只能说明该文提出的状态分析方法能够准确预测磨煤机在正常工作时的未来状态，并不能说明该方法是否能根据早期问题数据准确判断磨煤机将要发生的故障。因此，有必要再建立一个故障状态下的预测模型。

在检验模型预测故障的能力时，需要使磨煤机在故障状态下持续工作以获得相应实测数据作为评判标准。考虑到少煤情况对磨煤机的损坏相对较小，故该实验将模拟少煤故障。为了兼顾故障持续时间和样本采集量，将采样频率变为原来的两倍，时间则减少二分之一，采集点数量不发生改变。采用同样的神经网络对样本进行处理和训练，得到结果如图6 所示。

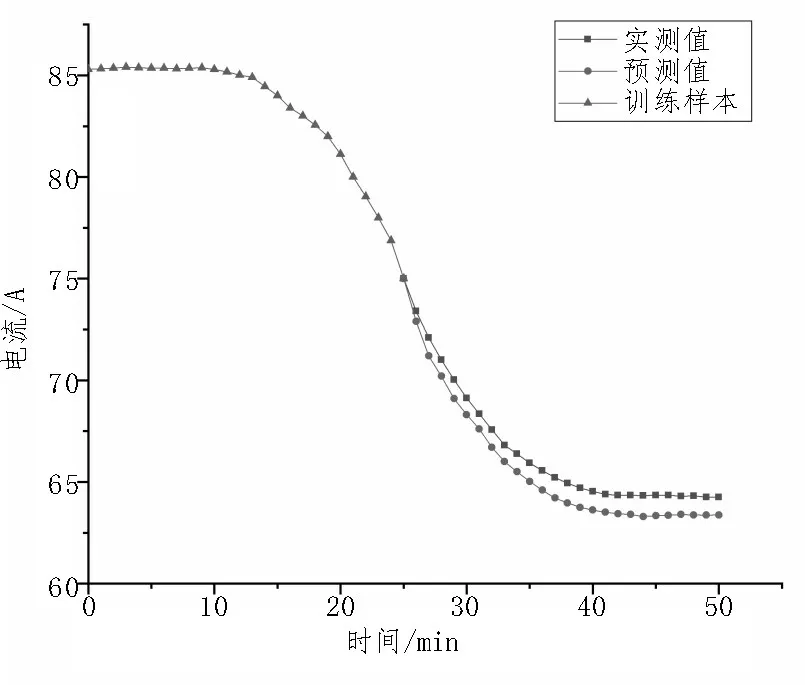
图6 少煤故障预测结果

3.4 煤量异常预测模型误差分析

当进煤量减少为正常煤量的3/4 时，磨煤机电流也变为额定情况下的约3/4，预测结果的趋势与实际情况是相符合的。通过计算可以得到少煤故障模型预测的均方根误差RMSE（I）=1.17 A，测量点的平均电流为Xobs,av（I）=74.59 A，模型的均方根误差 率γ（I）=1.57%。相比于正常运行状态下，模型的均方根误差率虽有所增大，但仍小于2%。因此，该模型可以准确预测煤量异常故障状态下的磨煤机电流变化。

4 结束语

该文以MPS225HP-II 型中速磨煤机为研究对象，选取正常运行状态下的磨出口温度和少煤故障状态下的磨煤机电流作为运行特征参数。以时间序列预测理论和LM_BP 算法为基础，完成BP 神经网络预测模型的构建[17]。将样本数据经过重构与预处理输入到已训练的预测模型中得到训练结果，使用均方根误差法分析模型预测的准确度。实验结果表明，无论是对于正常状态的预测还是故障状态的预测，模型的误差率均在2%以内。因此该神经网络预测模型可以对磨煤机的运行状态进行实时分析，从而对未来状态作出正确判断。

基于该文的研究方法所建立的模型虽能较好地对磨煤机的运行状态进行分析，但选取的单个特征参数难以做到全面地反映整个制粉系统的运行状态。具体到电厂磨煤机中则体现为影响因素更复杂的少煤故障状态预测模型所产生的误差率要大于正常温度状态预测模型[18]。所以要实现更为精确的运行状态预测，必须尽可能多地考虑系统中多个特征参数对于运行状态的影响。建立更为全面的多物理量预测模型，将是进一步的研究方向。