集成多种PWM 调制的直流无刷电机控制系统设计

张 洁，何文涛，3，刘 亚，3

（1.中国科学院微电子研究所，北京 100029；2.中国科学院大学，北京 100864；3.杭州中科微电子有限公司，浙江 杭州 310053）

直流无刷电机（BLDCM）控制系统一般采用脉冲宽度调制（PWM）技术实现电机调速[1]，常见的PWM调制方式有5种：H_PWM_L_PWM、ON_PWM、PWM_ON、H_PWM_L_ON、H_ON_L_PWM[2-3]。采用H_PWM_L_ON 调制模式时，直接比较端电压和电源负极电压即可得到反电动势过零信号，极大简化了反电动势检测电路的设计[3]，但该方法在换相时引起的转矩脉动较大[2]。文献[4]分析了SPWM 的基本原理及实现方法，采用SPWM 调制方法的控制系统实现简单、成本低，适用于低性能场合。SVPWM 技术的电压利用率高，能有效降低电机转矩脉动，转子旋转磁场接近圆形，是一种理想脉宽调制方法[5-6]，然而其原理复杂，实现步骤繁琐。文中针对上述问题，建立直流无刷电机的数学模型，提出H_SPWM_L_ON和H_SVPWM_L_ON 两种新型调制技术，并将该调制技术集成到一个实验平台进行对比实验。

1 数学模型分析

1.1 驱动方程

假设电机三相绕组完全对称，同时忽略定子齿槽、电机磁路不饱和及电枢反应对气隙磁通等的影响，得到BLDCM 三相绕组电压平衡方程如下[7]：

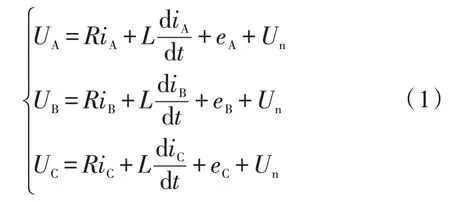
其中，UA、UB、UC为定子绕组的相电压，iA、iB、iC为相电流，eA、eB、eC为反电动势，R为各相电阻，L为各相自感，Un为中性点电压。根据式（1）建立电机的等效电路模型如图1 所示。

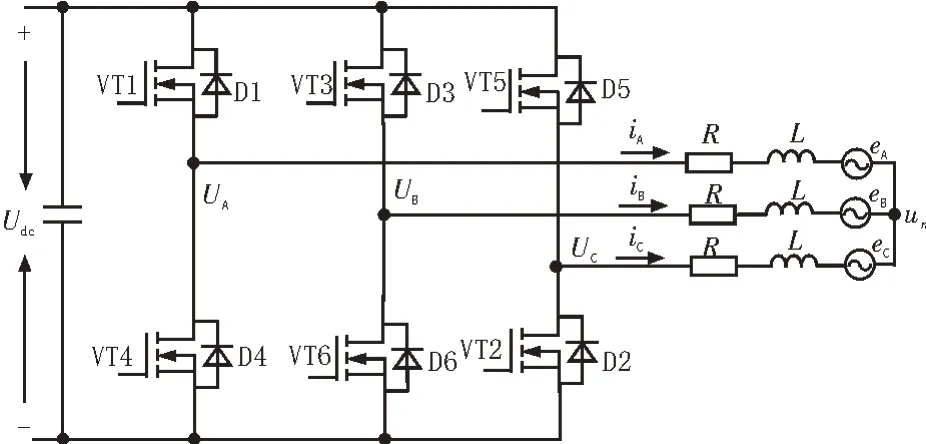
图1 直流无刷电机等效模型

1.2 反电动势方程

设计的驱动电路采用两两导通方式工作。假设AC 相导通，B 相关断，此时VT1、VT6 开关管导通，有iA=-iC，iB=0，代入方程（1）得：

又因为eA=-eC，得到中性点电压Un及B 相反电动势eB的值为：

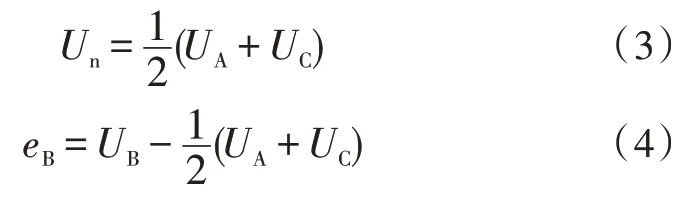
同理，当AB、BC 导通时，C、A 的反电动势为：

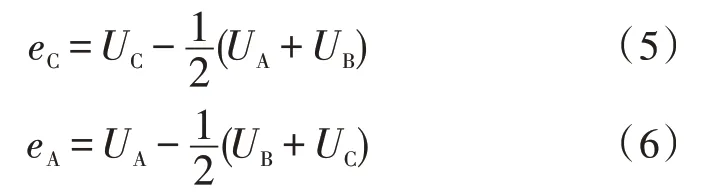
根据式（5）、（6）可知反电动势和相电压成正比，因此可以将反电动势过零检测电路转换为相电压检测电路。BLDCM 控制系统工作在两两导通方式时有6 种工作状态，反电势为底宽120°的梯形波[8]。假设反电动势幅值为E，C 相反电动势波形的数学表达式为：

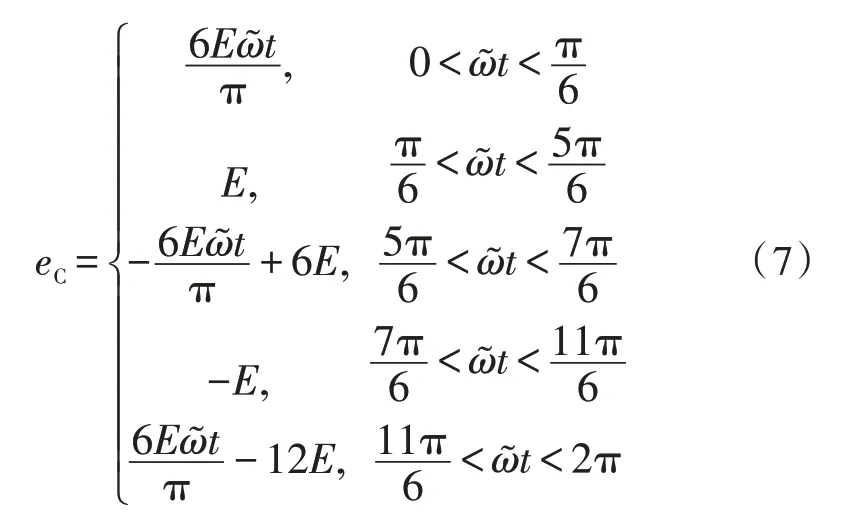
A、B 相反电动势和C 相反电动势幅值相等，相位分别相差120°和240°。

2 电路设计

BLDCM 控制系统可以根据位置信号分为有位置传感控制系统和无位置传感控制系统，文中设计了可同时支持上述两种控制系统的电路，结构框图如图2。该系统主要由数字控制电路、驱动电路和采样电路组成，文中重点阐述数字电路部分，其中包括启动电路、换相电路、速度检测电路以及PWM 调制电路等。

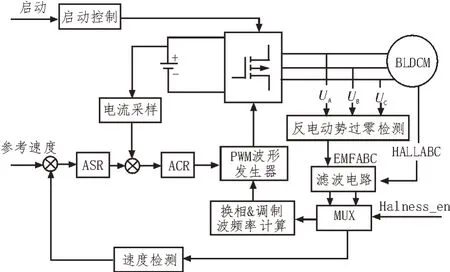
图2 直流无刷电机控制系统结构框图

2.1 换相电路

电机换相电路由驱动桥、换相逻辑和位置检测电路组成，通过控制电机定子绕组的导通顺序和导通时间控制电机的转速和转向。当电机工作在带霍尔传感器的BLDCM 控制系统时，可通过检测霍尔信号控制开关管的导通顺序，文中根据实验电机设计的六步换相规则如表1 所示。

表1 六步换相规则

根据式（7）可画出BLDCM 方波控制系统产生的反电动势波形图，其和霍尔传感信号对应关系如图3所示。当电机工作在无位置传感的BLDCM 控制系统下，反电动势过零点延迟30°就是电路的换相点，因此可根据反电动势过零信号设计无位置传感控制系统的换相逻辑。

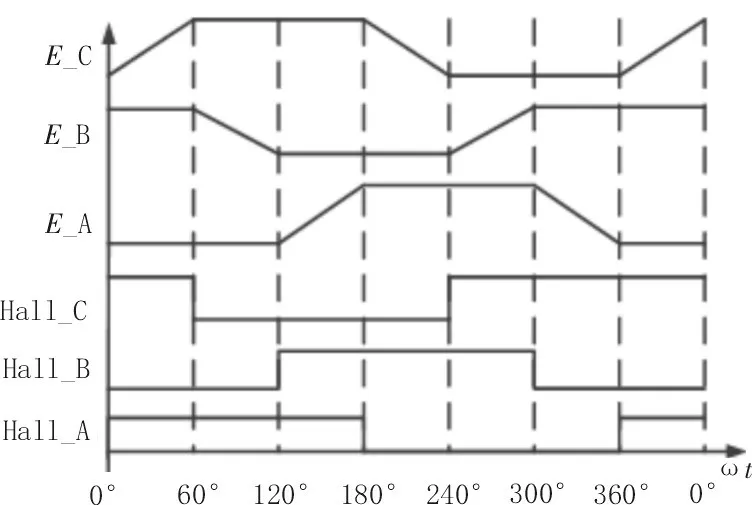
图3 反电动势和霍尔信号对应图

2.2 启动电路

BLDCM 工作在无位置传感控制系统时，电机在启动时转速极低，无法检测到反电动势过零点，因此需要设计启动电路控制电机转动至可连续检测到反电动势过零点的状态。文中采用传统三段式启动方法，首先选择并固定导通电机的一相，对电机转子进行预定位，然后根据电机的两两导通换相逻辑对电机驱动电路功率管进行通电，使电机旋转一周，最后根据反电动势过零信号切换到电机自控同步运转状态，完成电机自启动。

2.3 速度检测电路

速度检测电路的设计不仅影响换相时刻，还影响电机运行的平稳性，一般采用脉冲计数法来实现，即在规定的时间内对产生的脉冲进行计数，从而估算实际转速的大小。脉冲计数常用的方法有3 种：M法、T 法和M/T 法[9]。其中M 法和T 法分别在低速和高速运转时存在较大误差，而M/T 法弥补了M 法和T法的不足，同时结合了两者的测速优点，保证电机在高速和低速转动时都具有较高的精确度，原理如图4所示。M/T 法是在固定时间T内同时对电机转子转动圈数M1和频率为f的高频脉冲周期数M2进行计数，通过结合两个计数值得出实际转速的大小，转速计算方程如下：

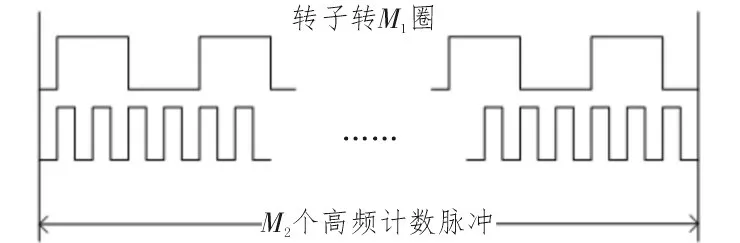
图4 M/T法转速测量

2.4 PWM调制电路

定子绕组在磁场中的感应电动势为[2]：

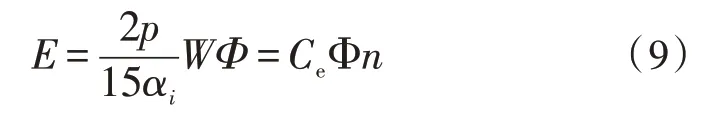
式中，p为电机极对数，αi为计算极弧系数，W为每相绕线组匝数，Φ为电枢绕组磁通量，Ce为电势常数，n为电机转速。

两两导通时电机的电磁转矩Te为：

式中，CT为转矩常数，I为绕组相电流。

假设U为电枢端电压，r为电枢回路电阻，将式（9）、（10）代入BLDCM 电压平衡方程U=E+2Ir中，得到电机转速方程如下：

式（11）表明，电机的转速由U、Φ以及r3 个变量控制。改变端电压调速法因应用范围广、调节简单被广泛使用[10]，通常采用PWM 调制技术调节端电压实现电机调速。PWM 调制方式有调制波为直流斩波的方波脉宽调制技术、调制波为正弦波的正弦脉宽调制（SPWM）技术和调制波为马鞍波的空间矢量脉宽调制（SVPWM）技术。马鞍波是通过对基波正弦信号注入三次谐波形成的，和正弦波相比，马鞍波的电压利用率更高，可有效减小负载电流中的谐波成分，降低转速波动[10]。采用正弦波或者马鞍波调制时，通过改变调制波的频率和幅值来改变电压的大小，达到调速的目的。文中将H_PWM_L_ON 调制法（图5）融入SPWM 和SVPWM 调制（如图6）理念，得到两种新型PWM 调制方式：H_SPWM_L_ON 和H_SVPWM_L_ON 调制。

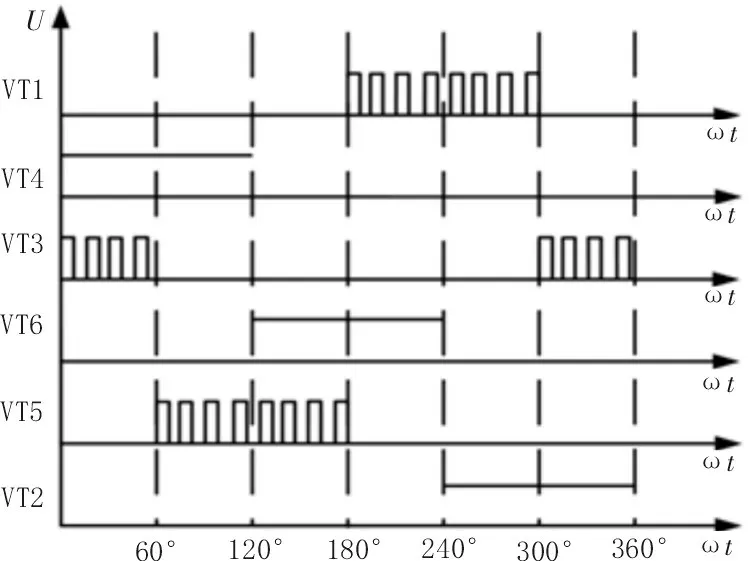
图5 H_PWM_L_ON调制方式

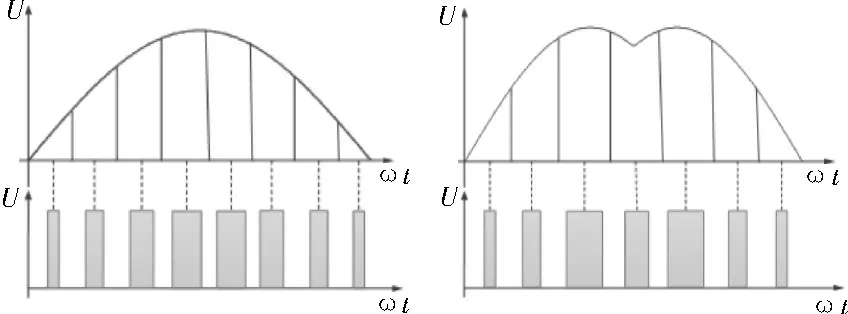
图6 正弦波、马鞍波调制PWM原理

为简化电路设计，减小电路面积，文中将正弦波和马鞍波幅值数据保存在表格中，采用查找表的方法确定3 个调制管的占空比，查找表格频率和输出幅度由实际速度决定。引入查找表代替复杂的矢量计算，可有效减少BLDCM 控制系统的计算量，加快PWM 占空比的加载速度。

3 实验结果分析

以上电机控制系统的设计方案均采用verilog 硬件描述语言实现，搭建如图7 所示的FPGA 实验平台进行系统功能验证。

图7 FPGA实验平台

实验使用的BLDCM 具体参数如表2 所示。电机转速为600 r/min 和3 000 r/min 时，分别对工作在3 种不同PWM 调制方式下的BLDCM 控制系统进行转速测量。由波特率为9 600 bps 的UART 串口采样实际转速，并通过上位机显示。

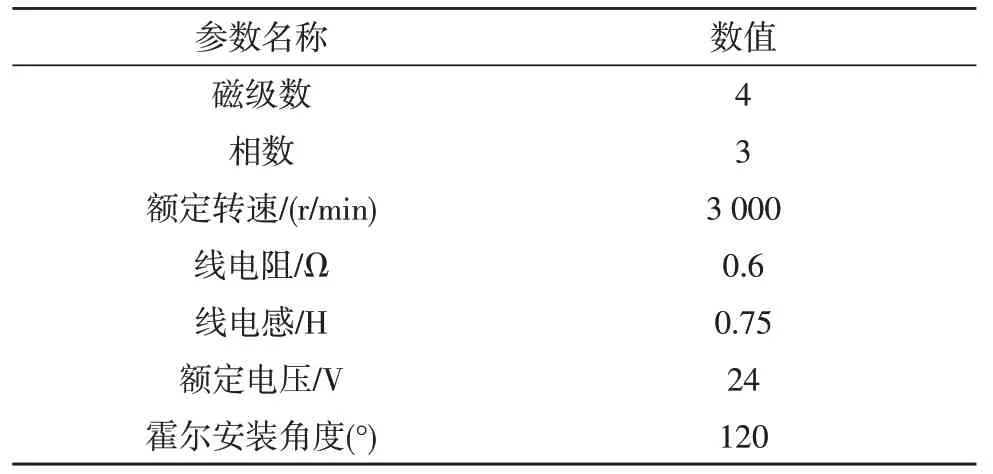
表2 实验主要参数

图8 为三相端电压测试波形，图9 为采用H_PWM_ L_ON 调制时的3 个上管PWM 波形，图10上为采用马鞍波调制时的PWM 波形，下为采用正弦波调制时的PWM 波形，实验波形和设计理论均相符。

图8 端电压波形

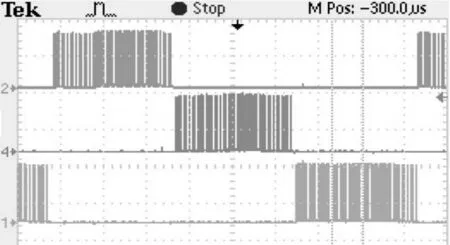
图9 PWM波形

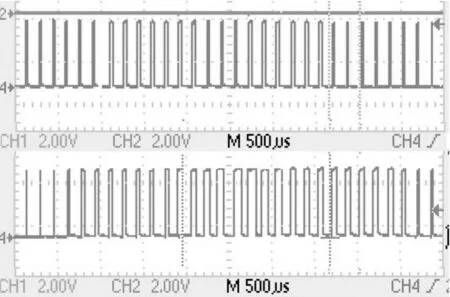
图10 正弦、马鞍波调制PWM波形

图11～13 为分别是电机转速为600 r/min 和3 000 r/min，采用3 种不同PWM 调制方式时的转速测量结果。

图11 H_PWM_L_ON调制时的转速曲线

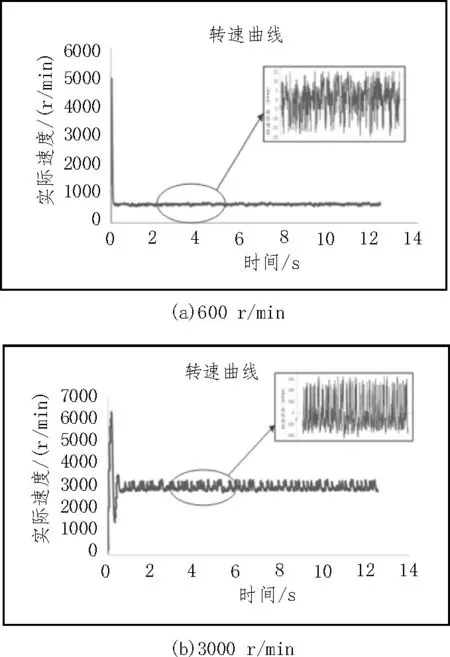
图12 H_SPWM_L_ON调制时的转速曲线

对图11～13 的实验结果整理得到表3，采用H_PWM_L_ON 调制的调速系统在保持高速转动时较稳定，但在低速时出现明显转速波动；采用H_SPWM_L_ON 调制的调速系统在低速转动时较稳定，但在高速时出现明显转速波动；然而采用H_SVPWM_L_ON 调制的调速系统，无论在低速还是高速转动时的转速波动都很小，调速系统最平稳。

表3 实验结果

4 结束语

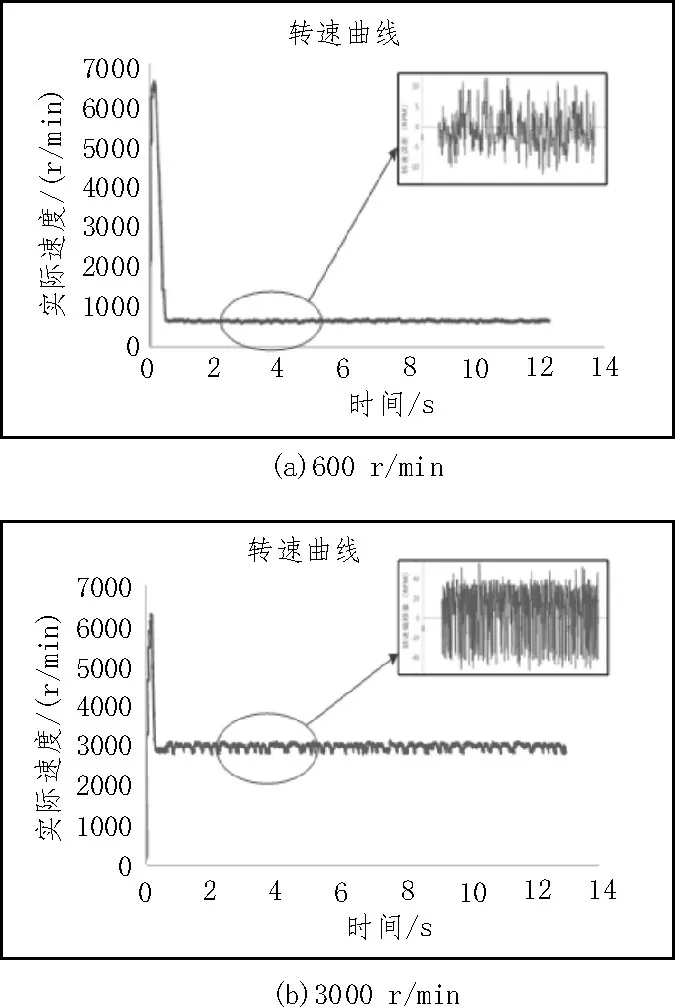
图13 H_SVPWM_L_ON调制时的转速曲线

文中将正弦波和马鞍波PWM 调制和H_PWM_L_ON 调制方式结合并应用到一个直流无刷电机方波驱动系统中[11-15]，分别在高速和低速转动时对3 种模式下的速度曲线进行测试和分析比较。通过实验结果可知，采用马鞍波脉宽调制方式的BLDCM 控制系统无论在高速还是低速运转时的转速波动都相对较小，大概保持在2%以内，和其他两种控制系统相比，调速系统最为稳定。