基于扩展状态观测器的随机隐Markov正跳变系统有限时间异步控制

任乘乘 宋 军 何舒平

(1.安徽大学人机共融系统与智能装备安徽省工程实验室,安徽合肥 230601;2.安徽大学电气工程与自动化学院,安徽合肥 230601;3.安徽大学人工智能学院,安徽合肥 230601)

1 引言

实际工程应用中,常常会出现如系统组件的随机故障、环境干扰以及非线性特性等导致操作点的突然变化等现象.这些突变现象一定程度上改变了各个子系统的工作状态.作为一类特殊的随机系统,Markov跳变系统常常被用来描述此类现象,并刻画各子系统之间的关联;基于此,学术界产生了许多创新性成果[1-2].然而,当前关于Markov跳变系统的研究成果中,大部分都是假设系统所设计的控制器可访问系统的模态信息,以实现控制器模态和系统模态之间的同步[3].实际上,由于系统信号延迟、信息测量不及时等原因,完全同步往往难以实现,进而导致设计结果的保守性.在此情况下,采用隐Markov建模[4-5],构建异步控制策略,不失为一种可行的方法.文献[6]针对时变Markov跳变系统,研究了有限时间区间内的异步输出反馈控制问题.在此基础上,作者进一步讨论了时变隐Markov跳变系统的异步滑模控制问题[7].文献[8]设计了非线性隐Markov跳变系统的异步滤波器.结合T-S模糊方法,文献[9]对连续时间隐Markov跳变系统的有限时间L2异步控制问题进行了分析.

另一方面,人们在研究动态系统时发现很多系统状态会出现一种非负现象,而且系统的初始状态和控制输入均非负时,其系统状态以及控制输出也是非负的,此类特殊的动态系统被称为正系统[10-12].实际上,学术界对含随机跳变参数的正系统的研究也日益广泛.针对含有输入饱和的Markov正跳变系统,文献[13]研究了其事件触发控制问题.文献[14]探讨了具有时变延迟的非线性Markov正跳变系统的非脆弱饱和控制问题.文献[15]采用线性规划的方法对具有饱和单输入的Markov正跳变系统的稳定性进行了分析.实际上,如果在正跳变系统设计过程中,控制器不能及时访问系统的模态信息,导致控制器模态和系统模态无法做到同步,如何进行分析与设计呢?更进一步,如果系统中含有未知不匹配扰动,导致对系统综合分析产生一定的影响,如何进行深入的控制与综合研究呢?基于这两个问题,本文引入扩展状态观测器(extended state observer,ESO)方法.

ESO不仅可用于实时估计系统的未测量状态,还可用于估计由系统未知参数或无法建模的动力学等造成的未知扰动[16-17].ESO方法不仅对系统模型的依赖性较小,而且对外部非线性扰动具有较强的鲁棒性[18-19].文献[20]结合ESO方法对三相功率变换器的滑模控制问题进行了研究.针对非线性反推液压系统,文献[21]利用ESO方法探讨了其输出反馈鲁棒控制问题.此外,ESO技术还被广泛用于电液伺服系统的自适应控制[22]以及DC-DC降压电源转换器系统的滑模控制[23]中.

本文针对一类含不匹配扰动的随机隐Markov跳变系统,研究基于ESO的有限时间异步控制问题.与现有结果相比,本文的主要创新点如下:

1) 首次结合ESO技术,研究随机隐Markov跳变系统的有限时间控制问题.放松现有成果中系统模态和控制器模态严格同步的限制,本文构建隐Markov模型,解决观测器/估计器与系统切换难同步问题;

2) 基于ESO方法通过引入一组扩展变量处理系统中的未知不匹配扰动,并设计合适的扰动补偿增益,补偿不匹配扰动在控制输出中的影响;

3) 结合随机Lyapunov-Krasovskii泛函方法,设计合适的基于ESO的异步状态反馈控制器和观测器,使得闭环随机隐Markov增广跳变系统是正系统,且有限时间有界.

符号说明:在本文中如果没有特殊说明,所有矩阵和符号都是标准的且具有兼容的维数.文中其他的数学符号含义如表1所示.

表1 本文符号含义Table 1 Symbols notations

2 系统描述

本文考虑如下定义在概率空间(Γ,Δ,Prob(·))的具有不匹配扰动的随机隐Markov跳变系统:其中x(t)=col[x1(t)x2(t)··· xn(t)]∈Rn是状态,y1(t)∈Rm是测量输出,y2(t)∈Rb是控制输出,u(t)∈Rp是控制输入,f(x(t),d(t),t)是不确定不匹配扰动函数,d(t)∈Rq是外部干扰,x0和r0分别为初始状态和初始模态.

定义1[10]对于任意给定的正初始状态x0>0、初始模态r0>0以及控制输入u(t)>0,如果对于任意时间t>0,随机隐Markov跳变系统的状态以及控制输出满足x(t)>0,y2(t)>0,则称该随机隐Markov跳变系统为正系统.

引理1[10]对于任意的r(t)=i ∈N,称随机隐Markov跳变系统(3)为正系统,当且仅当Ai为Metzler矩阵,Bi,Gi,C1i和C2i为正矩阵.

引理2[10]对于任意的r(t)=i ∈N,称矩阵Ai为Metzler矩阵,当且仅当存在一个随机正常数αi>0满足Ai+αiI ≽0.

由定义1和引理1知,如果隐Markov跳变系统(3)是正系统,那么系数矩阵满足:A(r(t))∈Rn×n是依赖于随机过程r(t)的Metzler 矩阵,B(r(t))∈Rn×1,G(r(t))∈Rn×1,C1(r(t))∈Rm×n,C2(r(t))∈Rb×n是依赖于随机过程r(t)的正矩阵.

考虑到随机隐Markov正跳变系统(3)中的不确定不匹配扰动,基于扩展状态观测理论[16,18],引入如下扩展变量:

注2实际工程应用中,由于系统信号延迟、数据丢包等不确定原因,往往设计的控制器无法直接访问系统模态.基于此,本文采用式(6)所示的观测状态ϵ(t)来获取控制器模态,系统模态则由隐藏状态r(t)表示.另一方面,由于本文设计的观测器通过观测系统的估计输出值进行反馈,观测值由隐Markov跳变系统的隐藏状态r(t)和观测状态ϵ(t)共同决定.因此,设计的观测器增益依赖于Z(t).

注3由于随机隐Markov跳变系统(3)的系统模态则由隐藏状态r(t)表示,此时测量输出y1(t)和控制输出y2(t)依赖于隐藏状态r(t).另一方面,本文设计的观测器增益依赖于Z(t),此时测量估计输出¯y1(t)和控制估计输出¯y2(t)同时依赖于隐藏状态r(t)和观测状态ϵ(t).

在系统分析与设计前,首先给出如下定义、引理和假设.

定义2[24]对于给定的常数T>0,c1>0,如果存在常数c2>c1>0、对称正定矩阵～Rik>0,使得对于任意t ∈[0T],下式成立:

3 主要结论

本文的目的是引入适当的扩展变量,设计合适的依赖于ϵ(t)的异步状态反馈控制器和观测器,使得相应的闭环随机隐Markov增广跳变系统为正系统,且有限时间有界.同时,设计并选择合适的扰动补偿增益K2k,补偿不匹配扰动在控制输出中的影响.

定理1 基于假设1,对于任意的r(t)=i ∈N,如果依赖于ϵ(t)的异步状态反馈控制器(6)使得(Ai+BiK1k)是Schur矩阵,且所设计的扰动补偿增益K2k满足

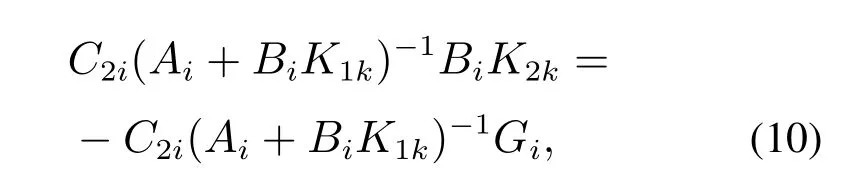
那么,异步状态反馈控制器(6)可以补偿随机隐Markov跳变系统(3)中不确定不匹配扰动f(x(t),d(t),t)对控制输出y2(t)的影响.

证 对于任意的r(t)=i ∈N,将依赖于ϵ(t)的异步状态反馈控制器(6)代入到式(3)中,可得

由式(13)可以看出,不确定不匹配扰动f(x(t),d(t),t)对增广跳变系统的影响在控制输出y2(t)中被补偿,并且扰动补偿增益K2k=−[C2i(Ai+Bi K1k)−1Bi]−1C2i(Ai+BiK1k)−1Gi.证毕.

注4定理1给出了保证不确定不匹配扰动f(x(t),d(t),t)对随机隐Markov增广跳变系统的影响在控制输出y2(t)中被衰减时的充分条件.在下面的定理2中,将给出充分条件保证基于ESO的闭环随机隐Markov增广跳变系统(8)是正系统、且关于(c1,c2,T,～Rik,ϖ)有限时间有界.

那么,称基于ESO的闭环随机隐Markov增广跳变系统(8)是正系统,且关于(c1,c2,T,～Rik,ϖ)有限时间有界.

进而,对于任意的t ∈[0T],对式(20)从0到t进行积分,可得

注5由式(18)知,不确定不匹配扰动f(x(t),d(t),t)及其变化率b(t)对增广跳变系统具有一定的影响.为了分析并得到基于ESO的闭环随机隐Markov增广跳变系统(8)是正系统且有限时间有界的充分条件,本文假设不确定的不匹配扰动函数f(x(t),d(t),t)及其变化率b(t)和外部干扰d(t)是未知有界函数,且满足假设1和假设2给定的有界条件.

注6定理2给出了保证基于ESO的闭环随机隐Markov增广跳变系统(8)是正系统、且关于(c1,c2,T,～Rik,ϖ)有限时间有界的充分条件.需要指出的是,由于矩阵不等式(14)中含有非线性项,不能直接利用MATLAB工具箱求解.在定理3中,本文将结合矩阵不等式转换法将式(14)中的非线性项进行处理,得到可直接求解Eik,K1k和K2k的线性矩阵不等式.同时,定理3将对系统(8)的正性进行分析,给出满足随机隐Markov增广跳变系统为正系统的充分条件.

因此,利用Schur补引理和特征值转换法,可由式(34)得到式(27)-(28).

接下来,证明基于ESO的闭环随机隐Markov增广跳变系统(8)是正系统.由式(29)-(30)可知(¯AiLiQk+¯BiSk)和¯AiLiQk是Metzler矩阵,−¯BiSk是正矩阵,并考虑到Sk=KkLiQk,可知(¯Ai+ ¯BiKk)LiQk和¯Ai LiQk是Metzler矩阵,−¯BiKkLiQk是正矩阵.因此,式(8)中的～Aik是Metzler矩阵.同时,由于～Gik和～C2i是正矩阵.结合定义1和引理1知基于ESO的闭环随机隐Markov增广跳变系统(8)是正系统.证毕.

4 数值算例

例1 考虑如下的具有两个模态的含有不匹配函数的二阶随机Markov跳变系统:

其中各模态参数的选取如表2所示.

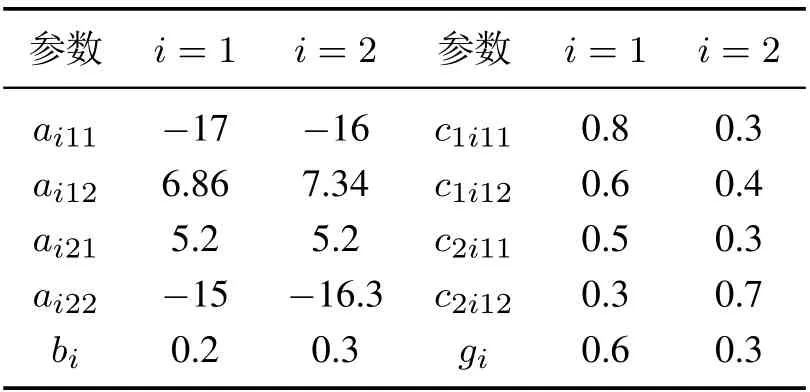
表2 二阶随机Markov跳变系统(35)参数Table 2 The parameters of the second-order stochastic Markov jump systems(35)

由式(35)和表4可知随机隐Markov正跳变系统的隐藏状态r(t)在集合N:={1,2}中取值,其系统参数矩阵为

不确定的不匹配扰动函数取f(x(t),d(t),t)=ex2(t)+sinx2(t).假设随机隐Markov正跳变系统的隐藏状态r(t)的转移率矩阵为

同时,考虑到控制器增益Kk依赖于观测状态ϵ(t),其中ϵ(t)∈M.假设随机隐Markov正跳变系统具有两种控制策略,即,M:={1,2},且依赖于Π的条件概率矩阵为

通过求解式(26)-(30),可以得到观测器增益Eik和控制器增益K1k为

同时,考虑到定理1,可以求解出扰动补偿增益分别为:K21=−2.7483,K22=−4.6064以及系统参数c2=3.3776.假设系统初始状态为:x(0)=col[0.6 0.6],c1=0.9,Rik=I.通过对系统在t ∈[0 3]内进行仿真,可以得到如下图1-5所示的仿真结果.

图1给出了隐Markov系统的跳变模态,其中图(a)是隐藏状态r(t)的跳变模态,图(b)是观测状态ϵ(t)的跳变模态.图2是基于ESO的闭环随机隐Markov增广跳变系统轨迹E{～ωT(t)～Rik～ω(t)},通过图2可以看出基于ESO的闭环随机隐Markov增广跳变系统(8)是正系统、且关于(0.9,3.3776,3,1,0.3)有限时间有界.图3-5分别给出了闭环随机隐Markov跳变系统的实际状态轨迹x(t)、估计状态轨迹¯x(t),估计误差轨迹e1(t),控制输出y2(t)、估计输出¯y2(t)和估计输出误差～y2(t).由图3-5可以看出本文所设计的异步状态反馈控制器和观测器的有效性.

图1 跳变模态Fig.1 The jump modes

图2 基于ESO的闭环随机隐Markov增广跳变系统轨迹E{～ωT(t) ～Rik～ω(t)}Fig.2 The state trajectory E{～ωT(t) ～Rik～ω(t)}of the closedloop ESO-based stochastic hidden Markov augmented jump systems

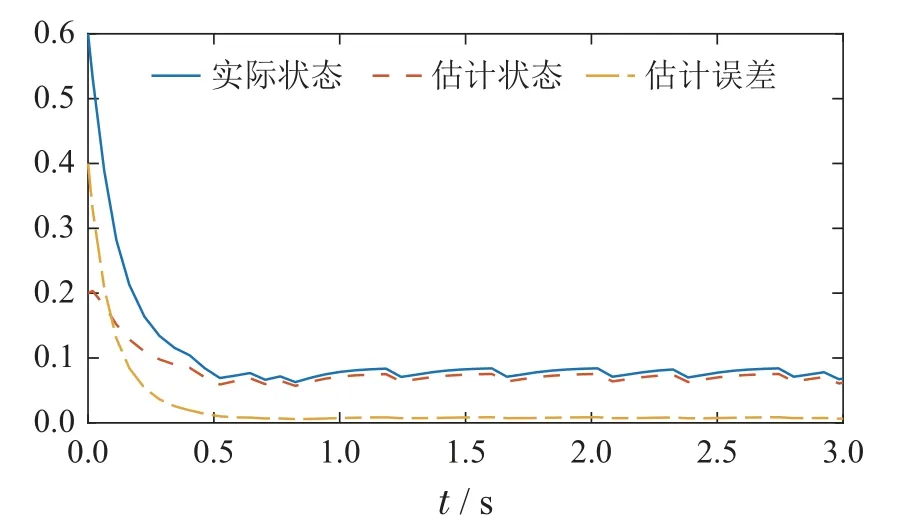
图3 闭环随机隐Markov跳变系统的实际状态x1(t)、估计状态¯x1(t)和估计误差e11(t)Fig.3 The real state x1(t),the estimated state¯x1(t)and the estimation error e11(t)of the closed-loop stochastic hidden Markov jump systems

例2 为了验证所设计的ESO方法的实用性,本文以RL电路系统为例,并考虑建模过程中的外部不确定不匹配干扰和随机故障影响,具体如图6所示.

假设图6所示的RL电路系统具有两个位置,以随机的方式从一个位置切换到另外一个位置且遵循隐Markov过程.外部不确定不匹配干扰和随机故障会影响电路系统的支路电流,进而会给整个电路的稳定性带来影响.为了解决外部不确定不匹配干扰和随机故障对整个电路系统的影响,本文采用ESO方法对RL电路系统进行分析与设计.由基尔霍夫定律,可由RL电路系统得

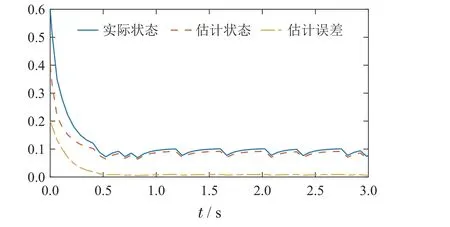
图4 闭环随机隐Markov跳变系统的实际状态x2(t)、估计状态¯x2(t)和估计误差e12(t)Fig.4 The real state x2(t),the estimated state ¯x2(t)and the estimation error e12(t) of the closed-loop stochastic hidden Markov jump systems

图5 闭环随机隐Markov跳变系统的控制输出y2(t)、估计输出¯y2(t)和估计输出误差～y2(t)Fig.5 The controlled output y2(t), the estimated output¯y2(t) and the estimation output error ～y2(t) of the closed-loop stochastic hidden Markov jump systems

图6 RL电路系统Fig.6 The RL circuit systems

由式(37)知Ai是Metzler矩阵,Bi,Gi和C是正矩阵.因此,RL电路系统(37)可建模为正系统.同时,考虑到如下表3所示的RL电路系统(37)各模态参数(R单位:欧姆,L 单位:亨):

表3 RL电路系统(37)参数Table 3 The parameters of the RL circuit systems(37)

不确定的不匹配扰动函数取f(x(t),d(t),t)=ei2(t)+sini2(t).对于任意的M:={1,2},选择与例1相同的的隐藏状态r(t)的转移率矩阵Π=[πij]和依赖于Π的条件概率矩阵ℵ1,ℵ2.通过求解式(26)-(30),可以得到观测器增益Eik和控制器增益K1k为

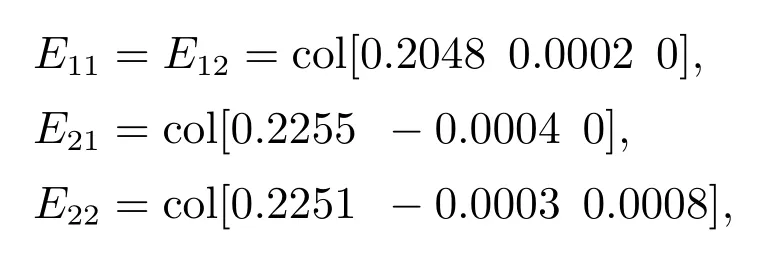
同时,考虑到定理1,可以求解出扰动补偿增益分别为

假设系统初始状态为:i1(0)=0.4,i2(0)=0.3,c1=0.6,Rik=I.通过对系统在t ∈[0 5]内进行仿真,可以得到如下图7所示的RL电路系统的控制输出、估计输出和估计输出误差仿真结果.

图7 电路系统的控制输出、估计输出和估计输出误差Fig.7 The controlled output,the estimated output and the estimation output error of the RL circuit systems

由图7可以看出本文所设计的基于ESO的异步状态反馈控制器和观测器可以补偿不匹配扰动在控制输出中的影响.

5 结论

本文研究了基于ESO的连续时间随机隐Markov正跳变系统的有限时间异步控制问题.为了补偿不匹配扰动对隐Markov跳变系统的影响,本文引入一组扩展变量将随机隐Markov正跳变系统转换成一组新的随机扩展系统.结合Lyapunov-Krasovskii泛函和线性矩阵不等式方法,给出了使得增广跳变系统是正系统,且有限时间有界的充分条件.同时,本文采用矩阵不等式转换法得到了可以直接求解观测器增益和控制器增益的充分条件.最后,通过数值算例和RL电路模型验证了本文所设计的异步状态反馈控制器和观测器的有效性和可行性.