离散时间部分状态反馈模型参考自适应控制
2022-01-08桑英丽张正强
桑英丽 张正强
(1.曲阜师范大学工学院,山东日照 276826;2.日照汇联众创智能技术研究院智能控制实验室,山东日照 276826)
1 引言
模型参考自适应控制(model reference adaptive control,MRAC)是自适应控制的重要研究方法之一,在连续时间系统和离散时间系统都有深入研究[1-2].模型参考自适应控制的目标是设计自适应律和控制器,使得被控对象输出渐近跟踪到参考模型输出,闭环系统所有信号有界.
由于系统状态难以获取,所以在实践中,满足一定假设条件下,大多采用容易获得的输出信号进行输出反馈控制,控制输入仅与输出信号和参考输入信号有关,不依赖状态信号.文献[1]基于观测器设计输出反馈MRAC结构


相对于输出反馈控制,状态反馈MRAC方案拥有更简单的控制结构.文献[4]对离散时间分段线性系统设计出切换自适应控制器,使闭环系统渐近稳定.文献[5]针对离散时间不确定性动态系统,提出了一种新的状态反馈模型参考自适应控制结构,有效地提高系统瞬态性能,并运用对数Lyapunov函数证明闭环系统的Lyapunov稳定性以及状态跟踪误差的渐近收敛性.但状态反馈控制依赖难以得到的全状态信息,限制了此控制方案的实际应用.
近年,针对连续时间系统,提出一种新的部分状态反馈控制方案[6-8].部分状态反馈控制以可测信号为反馈信号,巧妙地联系了全状态反馈控制与输出反馈控制,结合了两种反馈控制的优势,控制结构简单,受较少条件的限制,拓宽了反馈控制的应用前景,且可以实现闭环系统的稳定性以及对象与参考模型的渐近输出跟踪.文献[9]提出了新的离散时间模型参考自适应控制方案,采用部分状态反馈设计新的控制结构,实现线性不确定性系统的输出跟踪以及所有闭环信号的有界性,但文章缺乏相关引理、定理的证明.
本文提出部分状态反馈MRAC满足一定的输出匹配条件,通过引入辅助信号对离散时间部分状态反馈输出跟踪MRAC方案[9]作出严谨的输出匹配条件存在性、闭环系统稳定性以及渐近输出跟踪证明,对不同的反馈方式作出了仿真,证明离散时间部分状态反馈控制的有效性.
2 问题描述
考虑离散时间线性时不变系统

控制目标是设计部分状态反馈控制律使得闭环系统所有信号有界,对象(1)的输出y(t)渐近跟踪到参考模型输出ym(t).
参考模型定义为
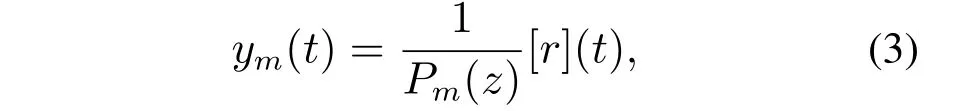
其中:Pm(z)是首项系数为1的稳定多项式(一般取为zn∗),r(t)是有界的参考输入信号.
在状态反馈输出跟踪控制问题中,作如下假设:
假设1Z(z)是首项系数为1的稳定多项式.
假设2P(z)的阶次n以及系统相对阶已知.
假设3 系统增益kp符号已知.
值得注意的是,输出反馈控制中反馈信号是状态信号的一个线性组合,也就是说,输出反馈是一类特殊的状态反馈;可测信号往往不仅是输出信号,得到的信息就不会局限于输出信号;另外,可测信号的阶次不大于系统阶次n.因此可测信号表述为

3 部分状态反馈标称控制设计
3.1 状态观测器设计
系统参数已知时,设计基于部分状态反馈的标称控制方案.在部分状态反馈控制中,本文将可测的信号y0(t)作为反馈信号进行控制设计,因此需要对状态信号进行处理.首先,增加假设
假设4 向量信号y0(t)=c0x(t),y0(t)是可量测信号并且满足(A,c0)能观测,rank(c0)= ¯n.
对于单输入单输出系统,y0(t)是¯n维信号,1 ≤¯n≤n,且y0(t)不一定包含输出信号y(t)或等于输出信号y(t).其次,作如下变换:


3.2 部分状态反馈控制器结构设计


3.3 部分状态反馈控制的输出匹配问题





同理,可以得到u(t)有界,ω1(t)有界.综上可知,控制器(18)可以实现输出匹配并且保证闭环系统所有信号的有界性,得证.证毕.
4 部分状态反馈模型参考自适应控制设计

4.1 自适应控制设计
采用直接自适应方法,通过估计标称控制器参数来处理系统的不确定性,得到以下自适应控制结构

4.2 稳定性分析
上节设计的自适应更新律有以下性质.
引理2 自适应律(50)-(51)保证了






5 仿真
考虑飞行器线性化动态模型系统如下:

仿真中,选取采样时间T=0.001 s,参考输入r(t)=0.01 sin(0.2t),Δ(z)=zn−¯n,Pm(z)=zn∗,x(0)=[0.1 0.1 0.1 0.1],ym(0)=0.01,γ=1.2,Γ=1.2I.自适应控制器参数的初始值选择为标称下控制器参数的90%.针对不同反馈信号,本文给出不同的仿真结果.本文采用部分状态反馈模型参考自适应控制方案,以二维信号y0(t)=[Qb/(rad·s−1);θ/rad]为反馈信号进行自适应控制,得到图1(a),图2(a),图3(a)所示的系统响应曲线.可以看出,控制信号和状态信号有界,实现了输出渐近跟踪,表明以一般可测信号进行反馈控制的有效性.
为突出新方案的优势,给出了状态反馈和输出反馈控制的系统响应曲线.图1是3种控制方案的输出跟踪误差信号曲线,部分状态反馈自适应控制相对输出反馈控制降低了振荡幅度,减少了响应时间;相对状态反馈控制虽增加了振荡幅度,但系统响应时间差别不大;图2是3种控制方案的控制信号,图3是3种控制方案的状态信号.

图1 部分状态反馈控制、状态反馈控制和输出反馈控制的跟踪误差信号Fig.1 Tracking error signals for partial-state feedback,state feedback control and output feedback control

图2 部分状态反馈控制、状态反馈控制和输出反馈控制的控制信号Fig.2 Control signals for partial-state feedback,state feedback control and output feedback control
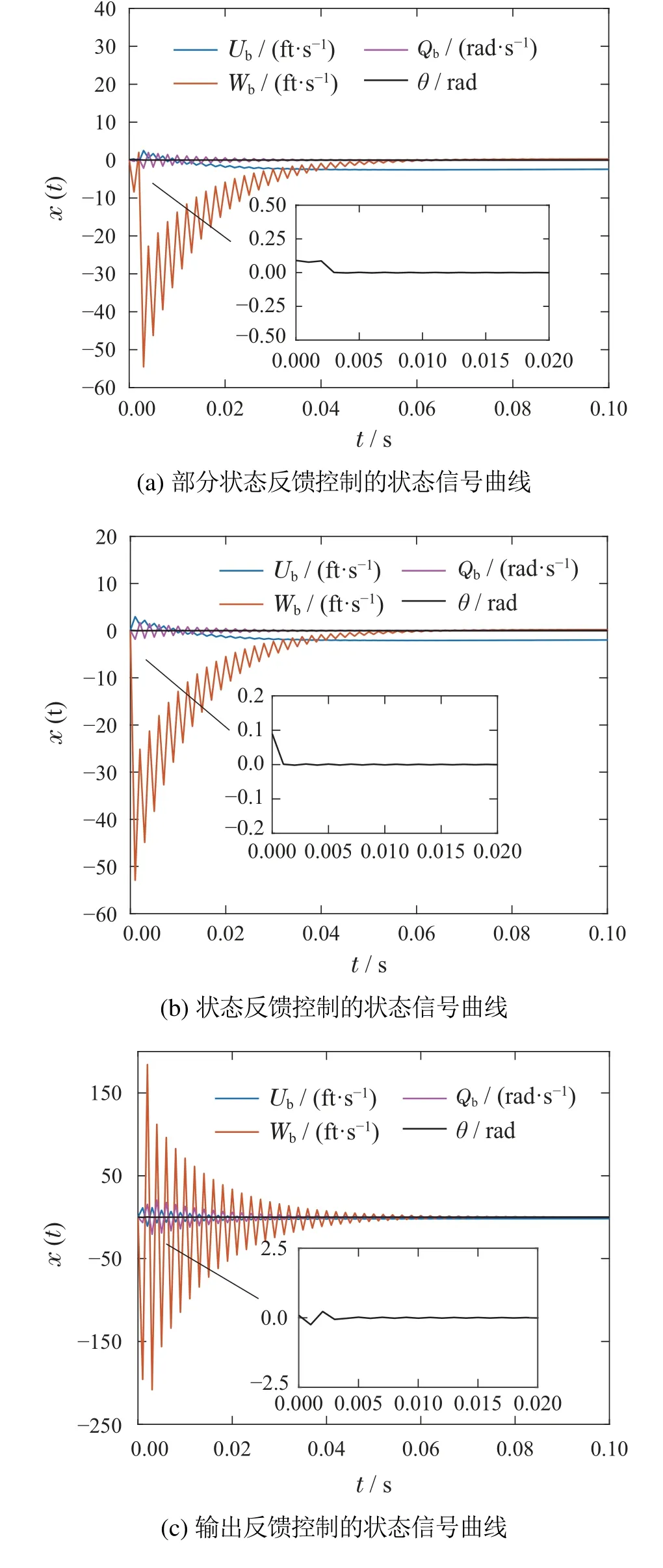
图3 部分状态反馈控制、状态反馈控制和输出反馈控制的状态信号Fig.3 State signals for partial-state feedback,state feedback control and output feedback control
新的控制方案相对输出反馈控制,具有更简单的控制结构,不依赖输出信号亦可以达到期望的控制结果.另一方面,新控制方案缓解了对状态信息的限制,依赖不超过系统维数的任意维可测信号进行控制,应用灵活.
6 结论
本文将部分状态反馈运用到离散时间系统,得到了更加灵活的模型参考自适应控制方案.本文不仅证明了输出匹配条件的存在性,还通过引入辅助信号,详细地证明了部分状态反馈模型参考自适应控制方案可以实现系统渐近输出跟踪以及所有闭环信号的有界性.仿真结果验证了这一控制方案的有效性.
