Enhanced active learning for model-based predictive control with safety guarantees
2022-01-08RENRuiZOUYuanyuanLIShaoyuan
REN Rui, ZOU Yuan-yuan, LI Shao-yuan
(Key Laboratory of System Control and Information Processing,Ministry of Education of China;Department of Automation,Shanghai Jiao Tong University,Shanghai 200240,China)
Abstract:This paper proposes an active learning-based MPC scheme that overcomes the shortcomings of most learningbased methods which passively leverage the available system data and result in slow learning. We first apply Gaussian process regression to assess the residual model uncertainty and construct multi-step predictive model.Then we propose a two-step active learning strategy and reward the system probing by introducing information gain as dual objective in the optimization problem.Finally,the safe control input set is defined based on robust admissible input set to robustly guarantee state constraint satisfaction. The proposed method improves the learning ability and closed-loop performance with safety guarantees.The advantages of our proposed active learning-based MPC scheme are illustrated in the experiments.
Key words:model predictive control;active learning;Gaussian process regression;dual control;information gain
1 Introduction
Model predictive control(MPC)[1-2],as the main control method to systematically deal with system constraints, has achieved remarkable success in many different fields, such as process control [3], autonomous driving[4-6]and robotics[7].MPC relies heavily on a suitable and sufficiently accurate model that describes the dynamics of the system. However, in many practical scenarios,models based on principles or data-driven approaches are subject to certain uncertainties due to incomplete knowledge of the system and changes in the dynamics over time,which can potentially lead to constraint violation, performance deterioration, as well as instability[8-9].
In the last few years,learning-based model predictive control (LB-MPC) [10-14] has become an active research topic, one direction of which considers the automatic adjustment of the system model, whether it is during operation or between different operation instances. Most researches on learning-based MPC focus on the automatic correction or uncertainty description of predictive models based on data, which is the most obvious component that affects the performance of MPC.Aswani et al.[10]firstly proposed a framework of LB-MPC which decoupled the safety and performance using two models: a model with bounds on its uncertainty and a model updated by statistical methods.This LB-MPC scheme improved the system performance through learning model while ensuring the robustness.Terzi et al.[12]constructed a multi-step predictive model with model uncertainties using set-membership, and proposed a robust MPC law in the control design phase.The authors in[13]obtained the predictive model using a nonparametric machine learning technique and then proposed a novel stabilizing robust predictive controller without terminal constraint.These studies require a prior strict bound on uncertainty,which is conservative in practice.To reduce conservatism,Di Cairano et al.[14]proposed a learning-based stochastic MPC for automotive controls using Markov chains. Cautious MPC was proposed in [15] that applied Gaussian process regression (GPR) to learn the model error between the true dynamic and prior model.To solve the problem of constraints, the author used chance constraints on both states and inputs. Based on this, Hewing et al. [4] applied GPR in the control of autonomous race cars which showed significant improvement on the performance in varying racing tasks.In [16],the authors reviewed these LB-MPC methods in detail and divided them into three categories:model learning,controller learning and safe MPC. As far as we are aware of, most LB-MPC techniques are passive learning methods. They account for the modeling challenge only by passively relying on available history process data,which cannot provide effective information as well as directly incentivizing any form of learning.In this work,we try to solve this problem by introducing the notion of active learning.
On the other hand, active learning or dual effect in control was first proposed by Feldbaum [17]that control inputs must have a probing effect that generates informative closed-loop data.[18-22]considered simultaneous identification and control of uncertain systems through dual MPC. Mesbah and Ali [19]summarized MPC with active learning and dual control. This article divided dual control into implicit and explicit methods: in implicit dual control, the optimal control problem is solved approximately;in the explicit one,the probing effect of the controller is directly taken into account in the control scheme in the form of additive cost function or persistent excitation.Heirung[20]presented two approaches to dual MPC, in which the controller is calculated based on minimization of parameter estimate variance and maximization of information. In [21], the authors not only considered MPC with active learning for systems with parametric uncertainty, but also dealt with the problem with modelstructure uncertainty. In terms of robust research, A robust dual MPC with constraint satisfaction was proposed for linear systems subject to parametric and additive uncertainty in [22]. In [23], the controller’s robustness was achieved through the multi-stage approach which uses a scenario-tree representation of the propagation of the uncertainties over the prediction horizon.A new development in dual MPC is the emergence of control-oriented methods to obtain model uncertainty descriptions related to pre-specified control performance [24-25], and we will not go into details in this work. However, these state-of-the-art approaches are limited to simple linear system dynamics which cannot be applied in complex systems, and most of them also fail to provide theoretical guarantees on safety and closed-loop performance.
In this paper, with the aim to improve the information quality of system operating data and enhance learning ability, we propose an active learning-based MPC (ALB-MPC) scheme based on information measures with safety guarantees.Contributions of our work are as follows: Firstly, the GPR mean function is used to learn the model error and construct the conventional LB-MPC scheme. Secondly, the state constraint satisfaction is robustly guaranteed by selecting control inputs from safety input set. Thirdly, we introduce information gain as dual objective in the optimal control problem and propose a two-stage procedure for ALBMPC. The next section presents the problem formulation and GPR method. Section 3 presents the common learning-based approach based on GPR and gives the notions of safety guarantee.Section 4 provides the definitions of relevant information measures and the twostep active learning control scheme. Finally, we illustrate the results with some numerical examples in Section 5 and end with the concluding remarks in Section 6.
2 Preliminaries
In this section,we define the notation,problem formulation and the basic content of Gaussian process regression.
2.1 Notation
A normally distributed vectorywith meanµand varianceΣis given byy~N(µ,Σ) and so a GP ofyis represented byy~gp().k∗∗is short fork(z∗,z∗)and[K]ijmeans thei-th row andj-th column element of matrixK. The superscriptdofmbmeans thatmhavedelements.xi|krepresents thei-step-ahead prediction of the state at the time stepk.ProjX(S)means the orthogonal projection of the setSontoX.ABis the set difference betweenAandB.I(z;D) denotes the information content of data setDafter adding new dataz.H(D)is the entropy of data setDandH(z,D)means the differential entropy at any data pointz.
2.2 Problem formulation
In this paper,we consider a discrete-time,nonlinear dynamical system
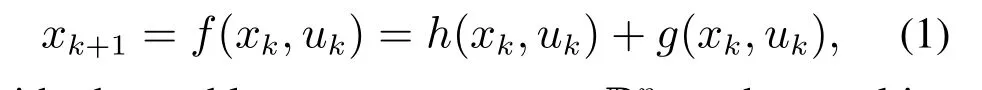
with observable system statexk ∈Rnxand control inputuk ∈Rnuat time stepk ∈N,wherenx,nuis the dimension of the state and input. We assume that the true systemfis not exactly known and use the sum of a prior nominal model and a learned model to represent it.Here,h(xk,uk)is a simple and fixed nominal linear model that could be achieved by first principles or people’s prior knowledge.g(xk,uk) is a learned part that represents the model error between the true behavior of the system and the prior model. We can use machine learning methods to model the learned part by collecting observations from the system during operation.Note that both the state and input are required to satisfy the following mixed constraints:

2.3 Gaussian process regression
Gaussian process regression(GPR)provides an explicit estimate of the model uncertainty that is used to derive probabilistic bounds in control settings. In this section, we will briefly introduce the concept of GPR and use it to learn the modelg.Gaussian process can be viewed as a collection of random variables with a joint Gaussian distribution for any finite subset.Given noisy observationsyof functiong:RnzRnd

Note that when GPR is applied in control, many research consider the propagation of uncertainty. In this paper, however, we employ the mean function to perform multi-step ahead predictions without considering the propagation of uncertainty for simplicity.Also,sparse Gaussian processes can reduce computation,but here we do not consider this method. For more specific knowledge about GPR, readers can refer to literature[26-27].
3 Learning-based MPC and safety guarantees
In this section, we apply GPR mentioned above to learn the model error and combine it with the prior nominal model to design learning-based MPC scheme.Also,we introduce the concept of robust control invariant set and safe control input set which guarantee the safety of the system.
3.1 Model learning and LB-MPC
The training dataykis generated from the mismatch between measurements ofxk+1and the prior nominal model during operation

wherezk=[xk uk]T.We then denote the recorded data set including all past control inputs and states available at time stepk
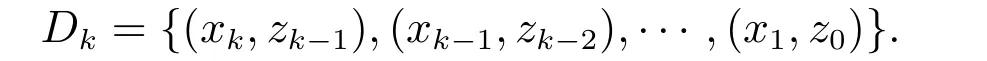
We use the data setDkto update the GPR model and make multi-step prediction combined with the nominal model at every time step.The model constructed is assumed to be equivalent to the true dynamics of the system.Then, the control inputs are determined knowing that the best prediction is available given the current system information.This method is a kind of certaintyequivalence approaches and the learning here is passive.
GPR mean function is used in the passively learning-based MPC approach.From equations(3)-(6)and the data setDk,the one-step-ahead predictive model can be constructed as follows:

x0|k=x(k).
Constraints on the inputs and states from(2)can be formulated as follows and these constraints are usually chosen based on physical hardware limitations,desired performance or safety considerations:

3.2 Safety consideration
In the LB-MPC problem, satisfaction of the state constraints cannot be guaranteed and the chosen input may not be safe. As illustrated above, we apply GPR mean function to learn the model error. Then, the confidence bounds of the GPR can be used to characterize model uncertainty.

Assumption 1 At every time stepk,the learned model satisfies constraintg(xk,uk)∈G(xk,uk)in(9)which is determined through offline learning.
Note that this assumption will not formally hold since the normal distribution has infinite support,but it is useful in practice and the confidence bounds are commonly used to model uncertainty.Combining it with the previous constraint on the state and input,we define set in(10):

It can be viewed as the subset of the graphGwhere the state and input constraints are both satisfied.Hence,we haveG= ProjX×U(Ω) which is the orthogonal projection of setΩ.Then the state-dependent set of admissible inputs can be defined as
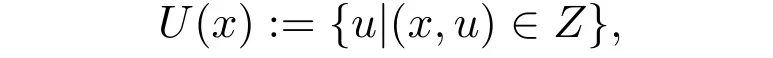
such that the set of admissible states is then
Based on these sets,we define the notions of robust control invariant set and safe control input set.
Definition 1 (Robust control invariant set) A setC ⊆Xis a robust control invariant set (RCI) for(1)(2),if for any,there exists au ∈U(x)such that

The setC∞⊆Xis the maximal RCI set if all other RCI sets are contained in it.Based on definition(1),we define the safe input set.
Definition 2 (Safe control input set) Given an maximal RCI,the safe control input set(SCIS)for statex ∈Xis

As a result,any control inputs can be chosen in the SCIS and keep the system safe.
Theorem 1 Based on Assumption 1,Definitions 1 and 2,at every time stepk,systemxk+1=h(xk,usk)+md(xk,usk)is safe that it always satisfies constraint(2)for any safe control inputusk ∈Πsafe.

For more details, some important and famous results that related to the recursion and the computation of invariant sets are in the surveys[28-29].The next main problem in this section is how to calculate predecessor set Pre(Υ).
Theorem 2 Given the set of admissible stateinput pairsΣ(Υ)and the set of tripletsΦ(Υ), the predecessor set ofΥis given by
Then the sets Pre(Υ) can be calculated and the proof can be referred to paper[28,32].Due to the confidence bounds in(9)are non-convex union of ellipsoids,

Given this polyhedral cover representations of the sets and the assumption that the nominal model is linear or piecewise affine, then the calculation of Pre(Υ)is outlined by the following procedures:
A)Compute the projection:Z=ProjX×U(Ω).B)Compute the inverse map:Φ=f−1(Υ).
C) Compute the projection:Ψ= ProjX×U(ΩΦ(Υ)).
D)Compute the set difference:Σ(Υ)=ZΨ.
E) Compute the projection: Pre(Υ) = ProjX(Σ(Υ)).
In order to achieve the results,we can use some important tools such as CPLEX,MPT3 for computing inverse images,set differences and projections.
4 Safety guaranteed active learning-based MPC
In this section,we propose a two-step procedure for active learning-based MPC.We first compute the most informative input sequence from the safety control set aiming to maximize the information of new data.Then,deviations from the desired input sequence are penalized in the constrained optimization problem. Specific methods are as follows.
4.1 Information gain and active dynamics learning
As previously presented, GPR is a non-parametric model which means we cannot use parameter estimate variance or Fisher information (FI) as the measure of model uncertainty reduction. So, we introduce an explicit information content objective to measure the reduction in estimated model uncertaintyI(xnew,unew;D), which denotes the information content of new dataxnew,unewadding to the history data setD.Here,we employ the concept of information gain which is commonly used to qualify reduction in estimated uncertainty.
Definition 3 Given the observation setD,when new dataznew= [xnewunew]Tis available, the information gain of the data is defined as

whereH(D) denotes the entropy before observation andH(D ∪znew)is the entropy when adding new data.I(znew;D), which is also known as mutual information, is often greater than zero. The greater the value is, the more information we have gained and the more uncertainty reduction is achieved.
As a result, we want to find the new data which maximize the information gain. Due to the fact that equation(13)is hard to be optimized[30-31]and needs to be approximated as follows:

this equation illustrates that the information gain approximates to the log value of the output variance at new data point.Furthermore, when a new data point is collected, both the GPR model and information gain change. We then define the active dynamics learning problem.

here,Nais the active learning horizon. Solving this problem at each time stepk, we get the most informative input sequenceUa:={ua,1,··· ,ua,Na−1}and guarantee the safety of active exploration because the control inputs are selected from the safety control input set.
4.2 Safe active learning-based MPC
In dual control paradigm,the control inputs not only need to satisfy control task performance but also have probing effect on system dynamics. So, we consider two objectives:one is the control task objectiveJtaskof equation(8)and the other is dual objectiveJdualwhich is achieved by penalizing the deviations from the desired input sequence.These two objectives are conflicting and we need to achieve a balance between them:J=Jtask+Jdual.
The safe active learning-based MPC optimization problem can be stated in(16)

whereαis a tuning parameter which determines the amount of dual effect. Whenα= 0, it means no dual effect or no active learning and it is a common control problem.Also,the control inputs are limited in the safe set which guarantees the safety of our ALB-MPC approach.
Remark 1The advantages of this two-step strategy lie that,(16)can still generates safe control inputs usingUaat timek−1 if(15)fails at time stepk.This optimization problem is simplified because we just penalize the deviations from the desired input sequence.
Remark 2The dual control problem can be divided into two phases: a control phase and an identification phase.Switch between the two phases is based on the model uncertainty that there is no need for active exploration when the uncertainty becomes small enough.
Finally,the safe active learning-based MPC(ALBMPC)strategy is outlined in Algorithm 1.
Algorithm 1 Safety guaranteed active learningbased MPC scheme.
Offline:Calculate(9)and determine the safe control input set in Section 4.2.
Online:Update data set,adjust the GPR model and design controller.
1)Initialize training datasetDk,control inputs and states,controller parameters
2)fori=1:N,do
3)Measure the current statexkat every time stepk;
4) Calculate the model errorxk −h(xk−1,uk−1)and update data setDk;
5)Learn the model and construct multi-step prediction model using(3)(4)(7);
6)Solve problem(15)according to the information content using predictive new data(13)(14);
7)Solve problem(16)and apply the first element of control input;
8)end for
5 Numerical examples
Two numerical examples are considered in this section. An Van der Pol oscillator and a cart-pole balancing task. Both examples are constructed such that we are able to illustrate advantages of our proposed active LB-MPC.
5.1 Van der Pol oscillator
The equation of the system dynamics is as follows:

In the model learning part, the initial states of the system arex1= 1,x2= 0 and the lower and upper bounds on the inputs areumin=−0.75,umax= 1.We first discretize this ODE equation to get a nonlinear discrete model. Then we also get a linear model of the system using successive linearization methods and treat it as the prior nominal model:xk+1=Axk+Buk,whereA= [1.4766−0.6221;0.6221 0.8544] andB= [0.6221;0.1456]. We use this nominal model to start the control process and collect related information to learn the model error.The initial training data is zero and updated online, then we learn a GPR model based on these data and the hyper-parameters are optimized by maximizing the marginal log-likelihood.Finally,we get the whole predictive model.In the MPC design,the modeling horizonNsis 20, the prediction horizon is chosen equal to control horizon:Np=Nt= 10, the weight matrices areQ= diag{[1 1]}andR= 1.The active learning horizon is selectedNa=5 and the tuning parameter of dual effectαis chosen 0 and 10(whenα= 0, it means no probing), then we will make comparison whenαis chosen these two different values.


Fig.1 Comparison of state trajectory in Vdp
5.2 Cart-pole balancing task
The schematic diagram of the inverted pendulum example is shown in Figure 2 and we aim to achieve an upright pendulum position of the pole by applying force to the cart. The continuous-time dynamics of the pendulum are given as follows:
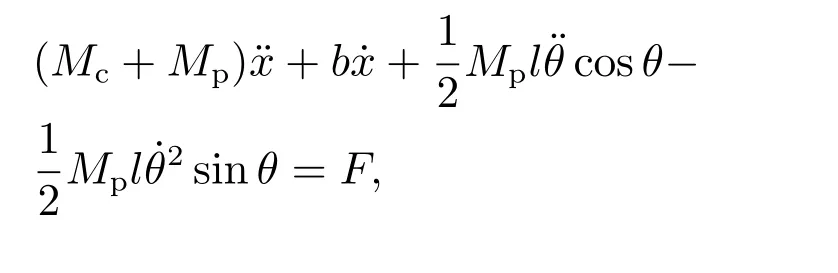


Fig.2 Schematic diagram of Cart-pole

The evolution of stateθis depicted in Fig. 3. We can see that these methods all enable adapting the model and stabilizing the system. The passive learning-based method in black color shows slower convergence than other active learning ones.When the parameter is chosenα= 5,the state converges faster than the one withα= 1. This result illustrates that our algorithm really introduces active learning and the tracking performance of the controller is improved effectively.The safety can also be reflected in this experiment that the inverted pendulum has not failed during the whole process.

Fig.3 Comparison of state trajectory in Cart-pole
6 Conclusion
In this work, we focus on the drawbacks of learning-based MPC methods that they lack effective data information and cannot excite any form of learning.we solve this problem by introducing active learning and dual effect,which enhances rapid learning ability and improves closed-loop control performance.The input and state constraints are also guaranteed in our method,and the advantages of the proposed method are illustrated in the simulations. Further research will be devoted to the control-oriented uncertainty description of the complex systems and the new form of dual objective.We will also study how to reduce the computational cost and focus on the application of our proposed method in process control.
