矩阵方程的分布式求解算法研究概述
2022-01-08李伟健曾宪琳洪奕光
邓 文, 李伟健, 曾宪琳, 洪奕光
(1.同济大学电子与信息工程学院控制科学与工程系;上海自主智能无人系统科学中心,上海 200092;2.中国科学技术大学自动化系,安徽合肥 230027;3.北京理工大学自动化学院,北京 100081)
1 引言
在被网络覆盖的大数据时代,基于多智能体网络的分布式计算和分布式优化方法的研究因其在自然科学和工程技术领域的广泛应用而受到了极大的关注.多智能体网络通常是对工程网络系统的抽象表示,用拓扑图节点代表网络中的智能体,节点之间的边代表智能体之间的信息交互关系,该网络结构既可能是固定的也可能是时变的.多智能体网络系统中的每个智能体具有一定的自主性,具有感知、计算和通信能力,分布式优化是通过多智能体利用自身局部信息和智能体之间的协调合作来实现全局优化目标[1-2].分布式优化问题中的一类主要研究方向是对全局目标函数的优化,而每个智能体仅已知其中一部分数据信息,允许智能体所计算的变量信息在邻居节点之间进行交互,从而实现全局求解.
一直以来,矩阵计算在数学理论和工程实践中都是至关重要的.矩阵方程求解是矩阵计算的一类典型问题,它与应用数学、计算技术以及工程控制领域的很多基本问题密切相关,例如,统计学和机器学习中针对数据的回归分析包括建模求解线性方程,或者在多目标预测、数据恢复等任务中建立低秩模型求解相应的矩阵优化问题;现实世界中大多数用于解释物理现象、进行仿真预测的建模分析会借助线性或非线性动态系统,而矩阵方程在线性动力系统的稳定性分析、控制器设计等问题中起着重要的作用,涉及Lyapunov方程、Sylvester方程等典型线性矩阵方程的求解问题;非线性矩阵方程Riccati方程在最优控制、鲁棒控制等相关理论的发展中也起到了重要的作用[3-7].矩阵方程的传统集中式解法在数值代数领域被深入研究,例如积分形式的解表达式和交替方向隐式(ADI)迭代方法[8-9],以及一些可以用来求解大规模矩阵方程的并行算法[10-11].但是在这类集中式算法和并行算法中,一般存在一个中心节点来收集、分发和处理数据和任务或者计算过程中需要直接利用整个数据矩阵,所以这些方法并不适用本文所探讨的基于多智能体网络的分布式矩阵计算情形.不同于并行算法的是,分布式算法中的智能体是平等且具有自主性的,它们各自掌控局部目标和相对的隐私数据,只需在其邻居智能体之间传递部分中间变量的信息.分布式网络的结构和去中心特征使得网络的灵活性和可扩展性增强,当网络中单一节点故障时,对整体系统造成的影响比较小.研究矩阵方程的分布式算法(不同于经典的并行算法),目前的主要方向是利用分布式优化方法来求解,本文将对现有的研究工作进行简要介绍:包括线性代数方程的分布式求解,几类典型矩阵方程的分布式求解,如Sylvester方程和Lyapunov方程等,以及其他类型的分布式矩阵计算问题,包括线性或非线性矩阵不等式等.
文中涉及的记号如下:Rm×n代表m×n的实矩阵空间.对于向量x,y和矩阵X,Y,〈x,y〉=xTy和〈X,Y〉F=trace(XTY)分别代表向量内积和矩阵Frobenius内积,‖x‖p和‖X‖F分别为其诱导的向量p范数和矩阵Frobenius范数.记0m和1m分别为零向量和全1向量,角标代表向量维数,0m×n和Im分别代表零矩阵和m×m的单位矩阵.Sm+和Sm++分别代表对称半正定和正定矩阵空间,其矩阵元素可以表示为X≥0m×m和X>0m×m.记PΩ(·)为凸集Ω上的正交投影算子.用图G(V,E)(可简记为G)描述多智能体网络的通信拓扑,其中节点集V={1,2,··· ,n}代表智能体集合,边集E ⊆V×V代表智能体之间存在通信,图的邻接矩阵和拉普拉斯矩阵分别记作[aij]和LG.不额外说明时,文中涉及的图默认为无向连通图.在矩阵数据的划分中,角标(上标或者下标)vi代表按行划分的第i个数据块,角标li代表按列划分的第i个数据块.
2 线性代数方程的分布式求解
线性代数方程作为矩阵方程的一种特例,一般表示为如下形式:

其中未知变量x是向量.关于方程式(1)的传统解法,在矩阵计算和数值代数领域的相关理论已经比较成熟,如Gauss消去法、Gauss-Seidel方法、Jacobi迭代法等[12].但由于网络系统的兴起,在相关应用的大规模计算中,集中式算法往往不再是第一选择,并且由于数据的分布式存储需求,集中式方法大多将不再适用.因此,在多智能体网络下探究线性方程的分布式解法有重要意义,近年来已经取得了不少的研究成果,参考文献[13-20].在多智能体网络中,通常假设每个智能体只能获取式(1)中的部分信息,可能包括但不限于矩阵A的某一行Ai和相应向量b的某个元素bi,然后通过与其邻居的信息交流(可以通讯状态变量但不交换原始数据)共同求解一致的未知变量x,即每个智能体对x的估计值xi最终达到一致.
方程式(1)的解有3种可能性:有唯一解、有无穷多解和无解.针对解的不同假设,学者们研究了多种类型的离散时间算法和连续时间算法来实现分布式计算.主要求解思路包括以下3类:
1) 借助各种投影算子结合一致性协议进行求解;
2) 转化成带等式约束的优化问题进行求解;
3) 特殊矩阵结构下的方程求解,如满足稀疏性.
关于第1种求解思路,重点在于寻找合适的投影空间以及确定投影算子的表达式.在联合强连通图的假设下,当方程至少存在一个精确解时,文献[14]提出了投影一致算法:


在连续时间算法的设计中,为了实现所有智能体i所求子问题的可行解xi ∈{y|Aiy=bi}趋于一致,通常有下列形式:

当网络通信图是无向连通图时,算法(5)-(6)都是指数收敛的.文献[22]针对满足联合强连通性的分段时不变切换图推广了算法(5).文献[16]利用一致算法和投影算子设计了两类求解按行分解数据A的分布式连续时间算法,分别是“一致+投影”方法和对投影项进行一致性操作的“投影一致”算法:
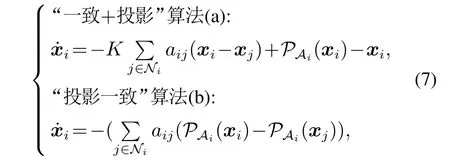
其中:xi(t)简记为xi,参数K为给定正常数,Ai表示仿射空间{x|Aix=bi}.文献[16]分析了这两种算法在通信拓扑为一致联合强连通的时变有向图时的收敛性.当方程式(1)存在唯一的最小二乘解时,文献[16]证明了式(7)中的算法(a)能够收敛到该最小二乘解的一个极小邻域内,在固定图前提下,算法(b)中所有智能体对解的估计值的均值将收敛到唯一最小二乘解.
在多数情况下,当线性方程式(1)有解时,求出其中任意一个解即可.如果线性方程式(1)的解的存在性未知或者该方程无解,那么寻找其最小二乘解[17,23-24]也是一类极其重要的问题.另外在某些情形下,需求出满足某些特殊性质的解,例如文献[25]在讨论压缩感知问题时,期望得到具有最小L1-范数的解,文献[18,26]期望得到最小L2-范数解.这类问题称作寻找正则解,相应的寻找正则解的分布式算法设计可参考文献[18,27]等.在寻求最小二乘解或者正则解时,常常用到第2类方法,把原问题转化成优化问题进行求解,可以灵活设置目标函数和约束条件,引入适当的变量进行求解.文献[17]中设计了Arrow-Hurwicz-Uzawa类型连续时间算法:

目前,大多数研究集中在对矩阵A按行划分再利用分布式方法求解式(1),也有一些研究考虑的是按列、按块或者求和形式等不同数据划分方式下的分布式解法.不同的数据划分方式可能由实际应用需求和不同网络节点的计算能力等多方因素决定,然后数据划分也直接影响着算法设计的适用性和不同算法的性能.文献[19]考虑的是每个智能体已知矩阵A的某一列或者多列的信息,求解的变量只是整体变量的一部分(所求方程解的形式为所有智能体估计变量的汇总,即x=col{x1,··· ,xN}),这种情况下也不需要所有智能体的决策变量达到一致.另外,文献[31]中的算法不需要对解是否存在做假设,可以验证出方程式(1)是否存在精确解,并且在解存在时能直接求出一个精确解,在精确解不存在时求相应的最小二乘解.文献[20]构建了一个双层网络结构,矩阵A的信息遵循先按行再按列或者先按列再按行的块状划分方式,在假设原方程有解的情况下,分别提出了“全局一致+局部守恒”和“全局守恒+局部一致”的两种对应的分布式算法,但是当不存在精确解时并不能直接用来求出最小二乘解.文献[20,31]中提出的算法也都可以从第2类型的分布式优化问题的层面来理解.
第3类求解思路是当求解方程中涉及的信息矩阵满足某些特殊结构时,会考虑一些有针对性的算法,例如针对稀疏矩阵特性的消息传递(message-passing,MP)算法.MP算法一般是指在通信过程中,通信拓扑图中的每条边上传递和更新信息变量,然后进行迭代计算.在与稀疏性相关的问题中,MP算法常被用来求解压缩感知问题[32-33].最近MP算法在求解稀疏的代数方程Ax=b问题中也有应用,文献[34]考虑矩阵A稀疏且满足广义对角占优条件的情况.在文献[34]的消息传递算法中,记A=[aij],与每个节点i有关的是对角数据aii和相应bi,若矩阵A中元素aij ̸=0,则代表其诱导的图结构中有一条边(i,j),由此获得的通信拓扑图为一个多圈图,选取其中任意一个节点作为根节点,把原本的多圈图展开为树结构再按顺序进行消息传递,每个节点根据树结构中所传递的消息来更新传递值和状态值,由此设计了离散的分布式算法.
现有的分布式求解代数方程的理论研究已经取得了很多优秀成果,但仍有一些不足限制了其实际应用:首先,现有算法对通信代价的分析较少,结合计算节点的通信和计算能力,研究通信效率和计算平衡的分布式算法设计可能是一个重要的研究方向;其次,矩阵的数据和迭代计算过程都可能存在一定误差,如何设计强鲁棒性的分布式不精确算法也是一个需要解决的问题.
3 线性矩阵方程的分布式求解方法
传统意义上,多以集中式方法来求解各类矩阵方程,当前很多实际应用中却关联着大规模网络系统,传统的集中式算法受限于整体数据的获取和所需要的计算能力和通信能力,而不能适应大规模方程计算的需求和分布式思想的发展,因此矩阵方程的分布式算法研究受到了研究学者们的广泛关注.线性代数方程可以看做矩阵方程的一种特例.
大多数线性矩阵方程可被概括为广义Sylvester方程的形式
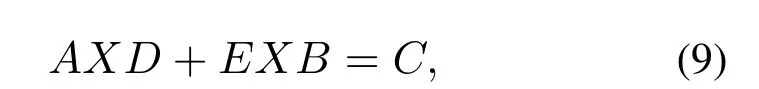
其中未知变量为矩阵X.还有其他多种类型的广义Sylvester方程在文献[9]中被研究.当矩阵E或B为零矩阵时,式(9)成为一类重要的矩阵方程AXD=C,求解其中变量X的计算问题在许多重要的应用中起着决定性的作用,例如矩阵的广义逆计算和广义Sylvester方程的求解[5,35-37],该方程的集中式算法在文献[37-40]等文中已有研究.另一类十分重要的线性矩阵方程是Sylvester方程AX+XB=C,即式(9)中矩阵D=E=I.在控制和自动化领域中,许多的Sylvester-型矩阵方程是其中一些基本问题和基本系统的原始模型.例如,通过设计机械振动系统的控制器,可以使用Sylvester方程实现特征结构配置[41-42];而当B=AT时,即为Lyapunov方程,该方程在线性时不变系统的稳定性分析中起着十分重要的作用[6].1884年,Sylvester提出了方程AX+XB=C有唯一解的条件[43],而后,众多研究学者们探讨了Sylvester方程及其广义形式的可解性条件[44-47],该方程有唯一解的充分必要条件为:矩阵A和−B没有公共特征值.到目前为止,学者们已经提出了该方程的许多集中式求解方法,例如,Hessenberg-Schur方法[48]、ADI迭代方法[49]以及Krylov-子空间方法[50]等.另外,考虑到求解大规模矩阵方程的需要,也有一些关于求解Sylvester类型方程的并行算法的研究[10-11].但是,注意到这些集中式算法和并行算法一般都要求有一个中心节点来处理和分发数据或者需要直接利用整个矩阵A,B,C,所以这些方法并不适合直接运用到本文所探讨的基于多智能体网络来求解的情形.
研究矩阵方程的分布式算法的动机主要来源于以下3个方面:
1) 把一般线性方程式(1)扩展到矩阵方程并不是一个平凡的推广,虽然向量化的矩阵方程也是可解的,但由于矩阵乘法带来的性质,具体的数据适用情况和算法形式还有待研究.基于多智能体网络下的矩阵信息的各种数据划分方式,分布式求解矩阵方程的过程与处理方程式(1)有较大差异.
2) 在大规模应用中,矩阵维数呈现爆炸性增长,如果采用集中式方法直接求解,对计算能力的要求是很高的.所以研究分布式求解矩阵方程算法的出发点在于缓解集中式计算的压力和构建去中心化的算法体系.
3) 针对某些应用情况比如在复杂网络中存在客观上独立的数据集,局部原始数据不能被他人所知,有着物理意义的这类矩阵方程所涉及的相关求解问题自然需求分布式求解方法.


对线性矩阵方程而言,方程的解有3种类型:唯一解、无穷多解和无解.当满足唯一性假设时,文献[51-52]等文献中研究其唯一解算法;当存在无穷多解时,有时候也只需要求解任意一个精确解即可[53-54],还可能需要求解的是满足特定条件(如范数最小)的精确解;当方程本身无解时,求解其最小二乘解通常也是值得研究的问题[55-56].有的方程会自带对未知变量的约束,如Lyapunov方程求解正定解,Stein方程求解某个凸集中的解.
关于分布式求解矩阵方程的工作,大多数是把解方程问题转化成标准的分布式优化问题后再进行求解的,其中的几个关键点在于:
1) 根据数据划分方式和参与计算的多智能体数目,待求解方程可以显式表示成包含局部数据的方程组;
2) 选取适当的目标函数,其形式为每个智能体的局部目标函数之和;
3) 按需添加一致性条件等约束,当约束中含有耦合等式约束时,需采取解耦方法,例如引入辅助变量列,把耦合约束拆分成多个单独的约束.
4) 对分布式带约束优化问题进行求解时,常用技巧包括原始对偶方法、投影算子、导数反馈等.
以下是现有工作中关于分布式求解几类矩阵方程的介绍,分别考虑不带约束和带约束的矩阵方程,以及其他几类矩阵相关的计算问题,包括线性矩阵不等式(linear matrix inequality,LMI)和非线性矩阵不等式等.
3.1 无约束的矩阵方程求解
考虑一般矩阵方程AXB=F或者Sylvester方程,未知矩阵变量X属于全矩阵空间,在无附加约束时求解其精确解或最小二乘解.
当方程式(9)的等式左边只有一项时,文献[57]首次用分布式方法求解了方程

并且分析了关于矩阵A,B,F的8种不同的行列数据划分方式.这里使用3个字母的组合代表数据矩阵A,B,F的划分方式,其中字母R和C分别代表行划分和列划分方式.这样3个矩阵则有不同的划分方式为RCC,RRR,RRC,CRC(另外4种划分可由以上4种划分经原方程的转置得到).针对每一种数据划分方式,文献[57]通过将方程等价转化成与个体局部信息相关的多个等式,并添加必要的一致性等式约束.以RCC划分为例,当利用包含n个节点的多智能体网络来进行求解时,引入辅助求解的变量Yi,满足关系式YiBli=Fli,AviXi=Yvii,其中数据Bli,Fli以及Avi为智能体i所知的局部数据信息.然后根据转化后的方程组设计相应的分布式优化算法,比如求解一个分布式优化问题
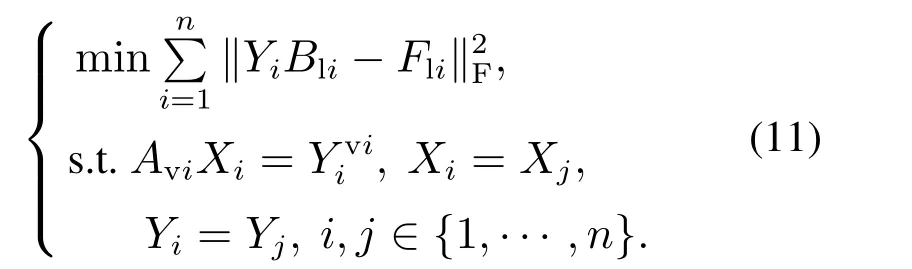
在网络通信图无向连通的假设下,X∗是方程式(10)的最小二乘解的充分必要条件是存在Y ∗=AX∗使得(1n ⊗X∗,1⊗Y ∗)是优化问题(11)的最优解.然后利用修正的拉格朗日函数L,即在一般的拉格朗日函数的基础上添加等式约束的最小二乘项,来设计分布式原始对偶算法,如图1.原始对偶方法(L函数的鞍点动力学)概述为

图1 RCC划分下的分布式原始对偶算法Fig.1 The distributed prime-dual algorithm under the RCC partition

其中:Zprimal表示Xi,Yi这类原始变量,Λdual表示优化问题(11)中根据等式约束引入的对偶变量.在某些情况下(如RRR,CCR划分),文献[57]中还添加了合适的导数反馈项来实现算法系统的稳定性.另外离散时间的算法也可以由类似方法写出.矩阵方程式(9)可以看做方程

在n=2时的情形.文献[53,55]中研究的是一般线性

文献[54,56]分别给出了Sylvester方程的精确解以及最小二乘解的分布式算法,实际上,按照数据矩阵A,B,C的行列划分情况,Sylvester方程式(15)等价于表1中的几种分布式形式.

表1 不同划分下Sylvester方程的分布式表达Table 1 The distributed forms of the Sylvester equation under different partitions

以上考虑的3类方程式(10)(13)(15),文[53-57]中都是采用“将求解问题转化成优化问题”的思路,对应于求解线性代数方程中的第2类方法.但是对比代数方程,矩阵方程中由于形式更复杂,会引入更多的对偶变量或者其他辅助变量来实现求解.
为了引入更少的变量,在同样的存在精确解的假设下,文献[58]求解的是式(15)的向量化的代数方程

特别地,考虑矩阵为方阵且行列数等于网络节点数m=r=n的情况.针对矩阵B和C的列划分,即每个智能体拥有局部数据A,Bli和Cli,智能体i求解子方程的解空间

在这个意义下,求解全局方程的解也就是求解多个凸集解空间的交集,即分布式凸交问题,对应于求解代数方程的第一类投影方法.因此,根据“一致+投影”的分布式算法,智能体按照各自动力学

更新变量,其中xi=vec(Xi)是智能体对未知变量的估计.式(19)与上一节求解线性代数方程式(7)中算法(a)一致,只是此处借助向量表示了矩阵变量和基于局部矩阵数据的投影子空间Si.文献[58]还证明了该算法的指数收敛速率随参数K的增加而单调非减的规律,当K趋于无穷时,明确了收敛速率的极限表达式.除此以外,文献[58]也考虑了行列划分中的RCC划分以及双层网络结构下的块状数据划分,在辅助变量的帮助下也分别提出了分布式算法和讨论了相应的收敛性质.
文献[56,58-60]都研究了Sylvester方程最小二乘解的分布式算法.其中,文献[56,59]在转化问题时选取了不同的等式关系改写了分布式优化问题,再利用原始对偶方法设计相应的连续时间算法来求解.文献[60]利用分数阶方法来设计分布式算法,其阶次设计有更高的自由度.
将求解无约束线性矩阵方程转化成分布式优化问题再设计算法的思路具有一定代表性,是可以适用于大多数常见的数据划分类型的,同时也可以统一处理精确解和最小二乘解的情形.虽然该类算法理论上可以达到指数收敛,但由于问题转化过程会产生多个等式约束从而需要引入多个辅助变量,导致每个智能体计算的变量规模变大,通信复杂度也会相应增加.文献[58]虽然表面上没有引入过多的辅助变量,但其讨论的数据划分方式受限,且需要假设精确解的存在性.未来考虑分布式矩阵计算的实际应用场景时,变量规模和通信代价的优化也将是值得研究的问题.
3.2 带约束的矩阵方程求解
部分矩阵方程的求解是带有约束条件的,一方面可能是由于方程本身的约束,比如Lyapunov方程是求正定解;另一方面是人为对解的选取,比如需得到对称解、核范数较小的解或者较为稀疏的最小二乘解等.而针对这类问题的一般策略是利用正交投影算子,在常规的变量动力学或者迭代关系式中额外添加一步投影.Lyapunov方程在系统稳定性分析中有着重要意义,一般带约束问题在如低秩矩阵数据恢复或推测中广泛应用.
针对Lyapunov方程,文献[51-52]分别考虑了离散时间Lyapunov 方程(discrete time Lyapunov equation,DTLE)和连续时间Lyapunov 方程(continuous time Lyapunov equation,CTLE)在某种特定数据划分下的分布式算法.实际上,当文献[51-52]中假设方程具有唯一解时,该解的正定性约束可以自然忽略.
DTLE的一般形式为

其中A,X,Q ∈Rn×n且矩阵Q和未知X都应是对称正定矩阵.文献[51]在假设方程式(20)有唯一解的前提下,讨论了矩阵A按行划分、矩阵Q按列划分后的分布式离散时间算法,对每个计算智能体引入辅助变量Yi,把式(20)改写成方程组

然后,根据方程组(21)中前两个的最小二乘残差以及一致性误差取定优化问题的目标函数.当等式满足唯一解假设时,该无约束优化问题的目标函数为严格凸函数,有全局最优解.每个智能体依照更新迭代规则更新变量Xi和Yi:

CTLE的一般形式为

文献[52]则考虑了连续时间Lyapunov方程(CTLE)的一种数据划分下的分布式算法,具体来说,CTLE的数据划分满足

其中Ω是矩阵空间Rm×n的一个闭凸子集.DTLE可以看作约束集为对称正定矩阵集的一类特殊的Stein方程.文献[61]针对Stein方程提出了一个基于投影和鞍点动力学的连续时间分布式算法.同样以数据矩阵A,B,C的RCC划分为例,式(25)等价于数据划分后的方程组形式,然后根据方程组写出相应的分布式优化问题之后,利用修正的拉格朗日函数L的鞍点动力学来设计算法,与第3.1小节中无约束解方程问题不同的是,因为变量Xi是限制在约束集里的,所以Xi的动力学需要借助投影算子:

文献[61]证明了所设计的分布式算法可以收敛到Stein方程的一个最小二乘解,特别地,当约束集Ω为全空间时,该算法(不带投影)满足指数收敛性.
另一种带约束的矩阵方程问题包括求方程的正则解,比如寻找一个稀疏解或者低秩解.文献[56]考虑了Sylvester方程的正则解问题

其中正则函数g(·)可以是非光滑凸函数,如‖X‖1.类似求最小二乘解的方法,把式(27)转化成一个非光滑函数的分布式凸优化问题再设计分布式算法求解.当假设Sylvester方程存在对称解时,为了解出一个对称解,文献[58]中针对向量化的代数方程,在“一致+投影”方法的基础上添加了一项新的对称化投影来实现求解.
为了寻找低秩解,文献[62]研究了满足矩阵线性关系式的核范数最小的解,文中模型可以用来求解满足代数方程的稀疏向量问题,低秩矩阵的补全问题等.文献[62]采取的方法是根据矩阵分析的有关性质把最小化非光滑的核范数转化成最小化另一个半正定矩阵的迹的问题,利用新的分布式优化问题设计原始对偶算法进行求解,部分变量还需要被投影到半正定矩阵空间.
针对带约束的矩阵方程求解问题,现有算法的关键在于引入投影操作,由于矩阵变量的维数可能较大且约束集合可能比较复杂,因此,投影的代价不能一概而论.为应对实际应用中投影代价高可能带来的挑战,研究无投影的分布式矩阵方程求解方法是一个重要的研究方向,其中一个可能的方法是借鉴优化中的条件梯度法.
4 其他分布式矩阵计算问题
除了上述线性矩阵方程的分布式求解问题,还有其他的矩阵计算相关的分布式算法的研究,包括分布式求解线性矩阵不等式(LMI)问题和非线性矩阵不等式问题等.
4.1 分布式LMI问题

即现在所说的Lyapunov不等式,它是LMI的一种特殊形式.Lyapunov还证明了这种方程可以被显式求解.通常,LMI有如下一般形式:

它表示了一类矩阵负定(或半负定)的不等式,其中系数矩阵均为对称矩阵,同时也可以看作变量x=col(x1,··· ,xm)的一个凸集约束条件.LMI问题应用广泛,在系统理论、控制理论和系统辨识等领域的很多问题都与LMI问题相关[63-64],例如非线性矩阵不等式(如代数Riccati方程)可以利用Schur补转化成一个新的LMI,特征值问题和半定规划问题都可以表述成是在LMI约束下的优化问题等等.
LMI问题的集中式解法包括椭球算法、内点法等[63].而在分布式设定下,比较有效的方法也是类似上一小节中求解矩阵方程的分布式凸优化方法.文献[65]研究了一类线性矩阵不等式组(LMIs)的分布式求解方法.参与计算的n个节点网络中的智能体i只能获取各自独立的一个LMI:

最终所有智能体需估计出同时满足n个LMIs的一致解[xi,1··· xi,m]T.首先,针对每个不等式,文献[65]中引入了两类松弛变量:半正定矩阵变量Yi和不小于某个负常数的实变量θi.借此把LMIs求解问题转化成带有等式约束和正定集合约束的分布式凸优化问题,然后通过添加一致性约束写出相应的拉格朗日函数,并设计了基于投影算子的分布式原始对偶算法.
半定规划问题(semi-definite programming,SDP)是一类实线性函数的极小化问题,在组合优化、控制理论和统计学等领域都有着重要的意义和应用价值[66].通常考虑的模型是变量同时满足一个LMI约束,具有的一般形式为

其中F(x)是满足式(29)中形式的LMI约束[67].在适当的形式转化下,SDP问题也可以直接表示成一个正定矩阵优化问题.文献[68]研究了关于SDP问题的分布式算法,具体考虑了以下形式的问题:

并采用带投影和导数反馈的分布式原始对偶算法进行求解,其中正定矩阵空间上的正交投影的计算是利用矩阵的特征分解给出确切表达式.值得一提的是,在已有的工作中,很多关于SDP的研究都是围绕稀疏矩阵的情况展开的,参考文献[69-72].在稀疏SDP的分布式算法研究中,文献[70]基于SDP的弦稀疏性提出了一阶分裂算法,文献[72]利用弦分解将大规模的SDP以原始或对偶形式进行降阶表述,应用了交替方向乘子法(alternating direction method of multipliers,ADMM)来进行求解.文献[71]依托一个固有的树结构,采用了消息传递方法来计算搜索方向和步长,收敛速度较快,但它要求了信息传递的顺序性.在文献[68]中,针对稀疏情况,数据矩阵中的局部数据F0,Fi均有相应的稀疏表达

其中EJi代表单位矩阵中相应非零行列组成的子矩阵,同时稀疏的正定变量Z也有弦图Gz和相应子矩阵ZCk的划分,从而矩阵Z的正定性可以由所有子矩阵ZCk,k=1,··· ,n的正定性给出[69].然后经过分布式设定下的矩阵处理,稀疏SDP情形下式(32)可以转化成如下分布式形式:


4.2 非线性矩阵不等式的分布式计算
除了线性矩阵方程和不等式问题,与非线性矩阵方程相关的求解问题[74-76]也一直受到研究关注.但由于非线性问题没有一般规则和统一形式,研究难度较大,通常会考虑和研究具有特殊形式的非线性方程或者不等式,典型问题包括代数Riccati等式和不等式问题.
Riccati方程是系统控制领域中的一类重要问题,在最优控制和鲁棒控制[77-78]等方面都有应用.该类方程的集中式解法例如不变子空间方法、基于牛顿的方法、ADI方法和加倍算法等[79-82]都需要利用全局信息来求解,不能直接处理分布式情况.在研究用分布式方法求解非线性矩阵等式或不等式的两种常用思路是:1)拆解集中式算法中的步骤,把其中的子问题转化成可以分布式求解的问题并设计相应算法;2)利用矩阵理论中的相关等价性把非线性问题转化成更高维的线性矩阵问题,再考虑进行分布式求解.
文献[83-84]分别研究了一类重要的非线性矩阵等式和不等式--连续时间的代数Riccati等式(continuous time algebra Riccati equation,CARE)
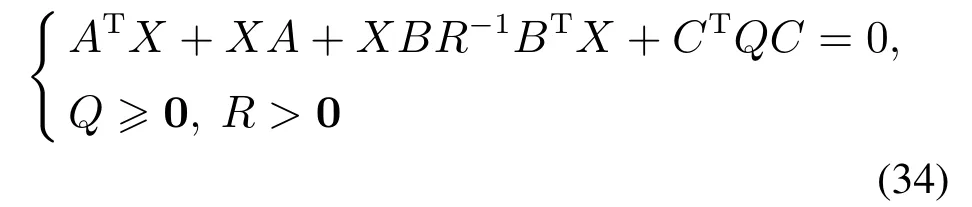
和代数Riccati不等式(algebra Riccati inequality,ARI)

并针对这两类方程各自的数据划分提出了相应的分布式算法.
文献[83]是以一类集中式算法--迭代细化方法(iterative refinement method,IRM)[80]为出发点来设计求解非线性矩阵方程式(34)的分布式算法,具体做法是把集中式IRM算法中的3个步骤拆分成3个子问题,再根据分布式数据划分下每个参与求解的智能体利用局部信息依次使用分布式迭代的离散时间算法来分别求解这3个子问题.IRM的算法步骤以及对应的分布式算法模块示意图如图2.其中,第1个子问题是包含非光滑项的耦合不等式约束,文中采取分布式邻近点梯度法来处理,避免了使用非光滑函数的次梯度信息;第2个子问题利用的是交替更新的原始对偶方法;第3个子问题采用了常用的分布式平均算法得到网络智能体合作估计的均值,最终3个子问题整合起来实现CARE的分布式求解.

图2 分布式IRM的算法结构示意图Fig.2 The structure of the distributed IRM algorithm
而文献[84]是利用Schur补定理把非线性问题(35)等价转换成了一个较高阶的LMI问题,同时通过引入松弛变量把不等式关系变成等式,然后针对新转换的分布式带约束凸优化设计了严格收敛、可求解ARI的分布式连续时间的带投影原始对偶算法算法.
现有的研究成果在计算效率方面仍存在一定改进空间,一方面是由于矩阵变量通常需要是正定矩阵,而维数较大的矩阵向正定矩阵集合投影的运算复杂度较高.另一方面是很多问题具有低秩等结构,现有的方法并未很好利用其特殊结构.因此,通过Burer-Monteiro分解方法或者流形优化等研究分布式矩阵求解算法,可能更好的利用矩阵的低秩等结构并避免正定矩阵的投影预算带来的复杂性,从而提高计算效率.
5 总结与展望
本文从矩阵方程类型、数据划分形式、方程解的类型、分布式算法等角度对矩阵方程的分布式计算方法的相关工作进行了简要介绍.当前矩阵相关问题的分布式计算仍然是一个重要的研究方向,但目前的算法中应用矩阵本身特殊性质的比较少,多是基于一般的分布式优化模型,由此会引入较多的辅助变量.如果能够进一步发掘矩阵特性并将其合理利用到分布式算法中,对优化计算复杂度等方面会有重要意义,在实际应用中也会有较大的提升空间.未来的研究方向可能还会包括:
1) 矩阵方程的随机和在线分布式求解方法.一方面,大规模矩阵数据中存在随机性和不确定性,利用随机优化算法可以降低算法计算复杂度,并求解概率意义下的未知矩阵变量;另一方面,矩阵中的数据可能随时间改变,或者是以数据流的形式获取,需要可以处理在线增量矩阵方程的方法.
2) 结构化大规模矩阵方程的低计算和通信复杂度的分布式求解方法.大规模矩阵方程常常具有一些稀疏性或特殊结构,研究这些情况下如何降低求解过程中的计算和通信复杂度以建立更高效的分布式算法,比如利用矩阵的稀疏或其他特殊结构和性质进行降维变换.
3) 针对矩阵优化问题的分布式高效求解算法.针对更一般的矩阵优化问题,如何结合矩阵的代数或者几何意义和分布式优化理论来设计有效的分布式算法具有重要的研究意义.
猜你喜欢
杂志排行
控制理论与应用的其它文章
- 基于扩展状态观测器的随机隐Markov正跳变系统有限时间异步控制
- Average cost Markov decision processes with countable state spaces
- 任意相对阶下非线性切换系统的事件触发漏斗控制
- 基于输出反馈和滑模控制的一类二阶非线性系统有限时间镇定方法
- Enhanced active learning for model-based predictive control with safety guarantees
- State-flipped control and Q-learning algorithm for the stabilization of Boolean control networks
