基于模板匹配的孔位与法矢检测算法
2022-01-07庄志炜石瀚斌杜兴华
庄志炜,田 威+,李 波,石瀚斌,杜兴华
(1.南京航空航天大学 机电学院,江苏 南京 210016;2.中国空间技术研究院 北京卫星制造厂有限公司,北京 100094)
0 引言
在产品数字化设计与制造过程中,数控系统根据产品的理论数学模型进行加工,但由于加工制造及工装定位等各方面的误差,被加工工件与其理论数模的一致性往往难以保证,因此若仅依靠理论数模来定位加工孔位,精度将不能满足装配要求。在实际加工过程中,需要根据工件的实际安装位置对加工孔位进行位置与法矢修正。例如在飞机部件自动化装配中,产品表面通常开设有若干组基准孔,作为产品定位的参考,在加工之前需要自动测量出基准孔的实际位置,从而实现飞机部件的精确定位[1-4]。准确识别和定位产品上的基准孔是自动化装配系统的关键技术之一,目前,多数装备采用工业相机或者2D激光轮廓仪进行孔位检测。
基于单目视觉的孔位检测技术已较为成熟,设备简单,且算法容易实现。杨小丹等[5]采用视觉系统进行机器人制孔设备的基准孔找正,但该方法只适用于检测孔在X、Y方向上的位置,在深度Z方向上的检测精度不高,且不能测量出孔的轴线方向(即孔的法矢)。例如在飞机自动钻铆过程中,在将铆钉自动插入曲面上的一个铆钉孔时,需要同时测量出该铆钉孔的位置和法矢信息,才能精确地将铆钉插入孔中,因此基于单目视觉的孔位检测技术便不再适用。Electroimpact与Boeing共同研制了机器人自动制孔系统ONCE(one-sided cell end effector), 用于F/A-18E/F超级大黄蜂机翼后缘襟翼蒙皮到底座的连接制孔,其采用相机视野中心十字准线与基准孔对齐来完成定位,但检测过程需人工干预[6]。而其第二代产品则实现了对基准孔特征的自动识别,并计算基准孔实际位置与理论位置的偏差从而进行修正[7],但该方法容易受环境光源的干扰,从而导致测量结果不准确。
为了更精确地检测孔的位置,出现了基于2D激光扫描的孔位检测技术。将2D激光轮廓仪安装在直线运动机构上即可获取到孔周边的三维点云,对点云进行一定的处理可计算出孔的位置和法矢信息。孙海龙等[8]利用2D激光轮廓仪扫描得到待测平面的点云,通过设置所有点云数据点到拟合平面的距离阈值达到滤除孔边缘噪声点的目的,该滤波算法只适用于平面,不适用于曲面。另外,他通过在X、Y方向上提取孔的边缘点,最终拟合出孔位圆并计算出孔中心坐标,这种基于边缘检测的孔识别算法只有在2D激光轮廓仪能扫描出理想的点云时才能适用,当点云有瑕疵时,不能很好地识别出孔特征。将三维点云与二维图像相结合是计算机视觉领域中一个很有前景的方法[9],谭小群等[10]提出一种基于线激光扫描与图像处理结合的基准孔检测方法,将线激光扫描获取的三维点云数据转换为二维灰度图,再使用边缘检测算子提取轮廓,从而获得基准孔的中心位置。但该方法同样仅适用于理想情况下无表面缺陷的点云,当出现大面积噪点时,边缘提取算法无法识别出基准孔的边缘,只能通过手动选取感兴趣区域,以提高孔的识别度,因此该算法无法满足自动化装配的需求。
随着复合材料在飞机上的大面积使用,自动钻铆系统对孔位检测提出了更高的要求[11]。采用2D激光扫描孔时,由于复合材料的强吸光特性,扫描得到的待测表面点云存在大面积瑕疵,传统的基于边缘检测的孔位检测算法已无法在复合材料飞机部件上使用。另外,目前基于2D激光扫描的孔位检测技术只能用于孔的位置测量,还不能测量出孔的法矢,必须采用一种新的算法来精确检测出孔的位置和法矢。
针对上述问题,本文提出一种基于模板匹配的孔位与法矢检测算法。首先利用2D激光轮廓仪扫描获取待测平面的初始点云信息,接着采用改进型中值滤波算子对获取的点云进行滤波降噪等预处理,然后将点云的z坐标值二值化,自适应构造出孔模板,并执行模板匹配以识别出孔特征,最后计算出孔的位置和法矢。
本文主要有以下创新点:
(1)提出采用模板匹配法进行三维点云中孔的识别定位,并利用感兴趣区域(Regions of Interest ,ROI)进行孔特征最终判别,提高了孔的识别率;将三维点云进行二值化处理,简化了模板匹配的计算,提高了匹配效率。
(2)提出孔模板自适应构造算法,算法可根据实际扫描得到的点云特征以及给定的孔径自适应构造孔的模板,省去了人为构造孔模板的繁琐程序,提高了孔的匹配度。
(3)采用奇异值分解(Singular Value Decomposition,SVD)的方法拟合孔邻域内的点云,以邻域平面的法向作为孔的法矢,实现了孔的法矢测量,利用改进型中值滤波算子对孔边缘进行降噪处理,提高了孔的法矢测量精度。
1 点云获取与预处理
1.1 点云数据的获取
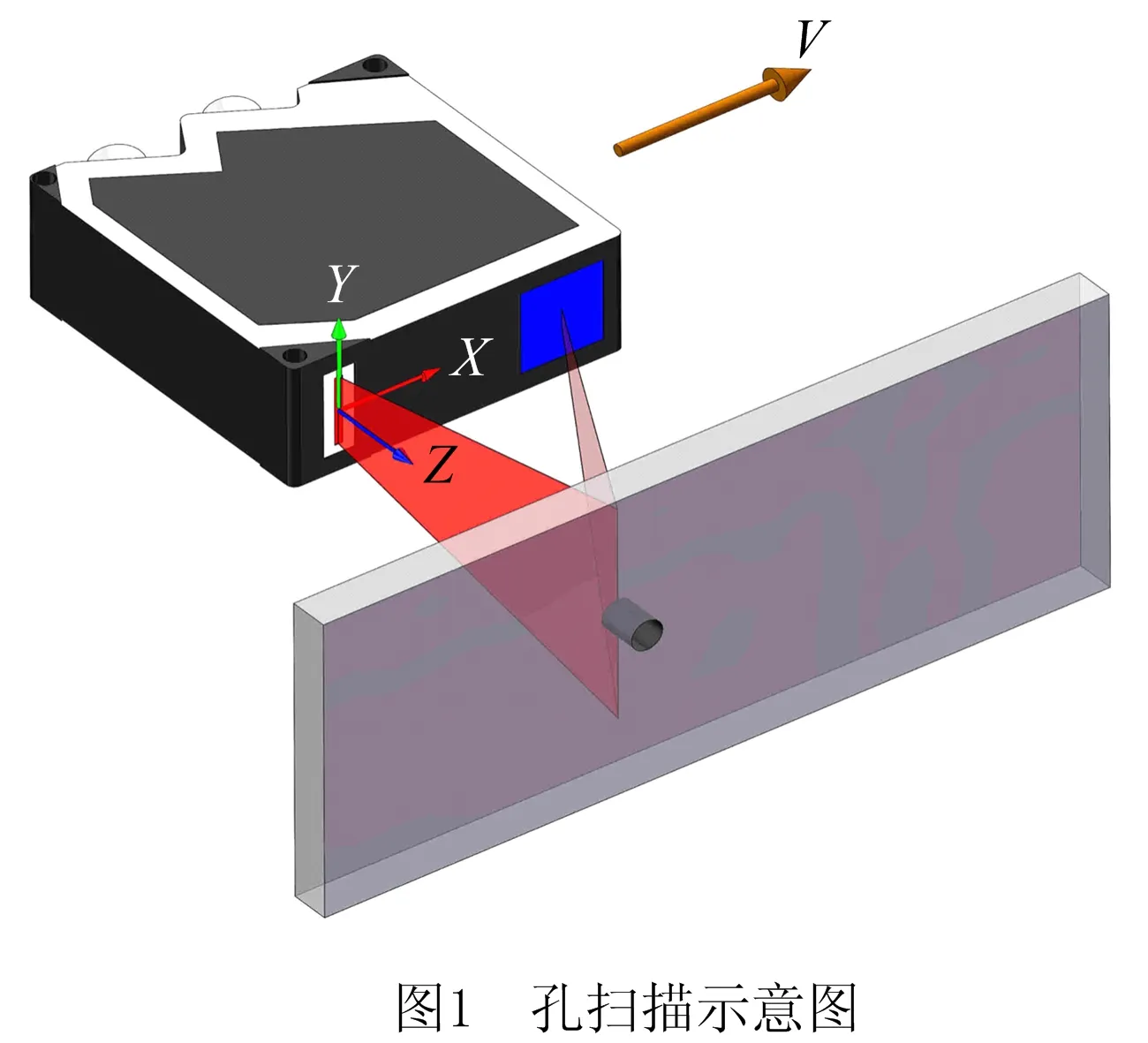
利用2D激光轮廓仪对孔进行扫描,如图1所示。2D激光轮廓仪搭载在直线电机上,可沿着X方向以速度V匀速直线运动,通过电机编码器的数值可计算得到X方向的位移x。轮廓仪可以测量出到被测表面的距离信息(Z方向)以及沿着激光线的位置信息(Y方向),以轮廓仪发射中心为原点的二维坐标系内,轮廓仪测量输出一组二维坐标值(y,z)。同时,采集直线电机编码器数值与轮廓仪测量数值,便可扫描得到被测表面的三维点云的坐标(x,y,z),最终可得到3个row×col的矩阵X0、Y0、Z0(其中row为矩阵行数,即每条线轮廓采集的点数;col为矩阵列数,即采样次数),分别记录了点云在X、Y、Z三个方向的位置。对点云进行处理,可得到孔在轮廓仪坐标系下的位置和法矢信息,通过坐标变换,可计算出孔在机器人基坐标系下的位姿,从而控制机器人运动到指定的位置。
以两种不同材料的待测工件为例,分别对这两种工件的表面进行扫描,其中工件1为表面喷漆的材料,工件2为表面铺设铜网的复合材料,扫描两种工件表面得到的原始点云数据如图2所示。
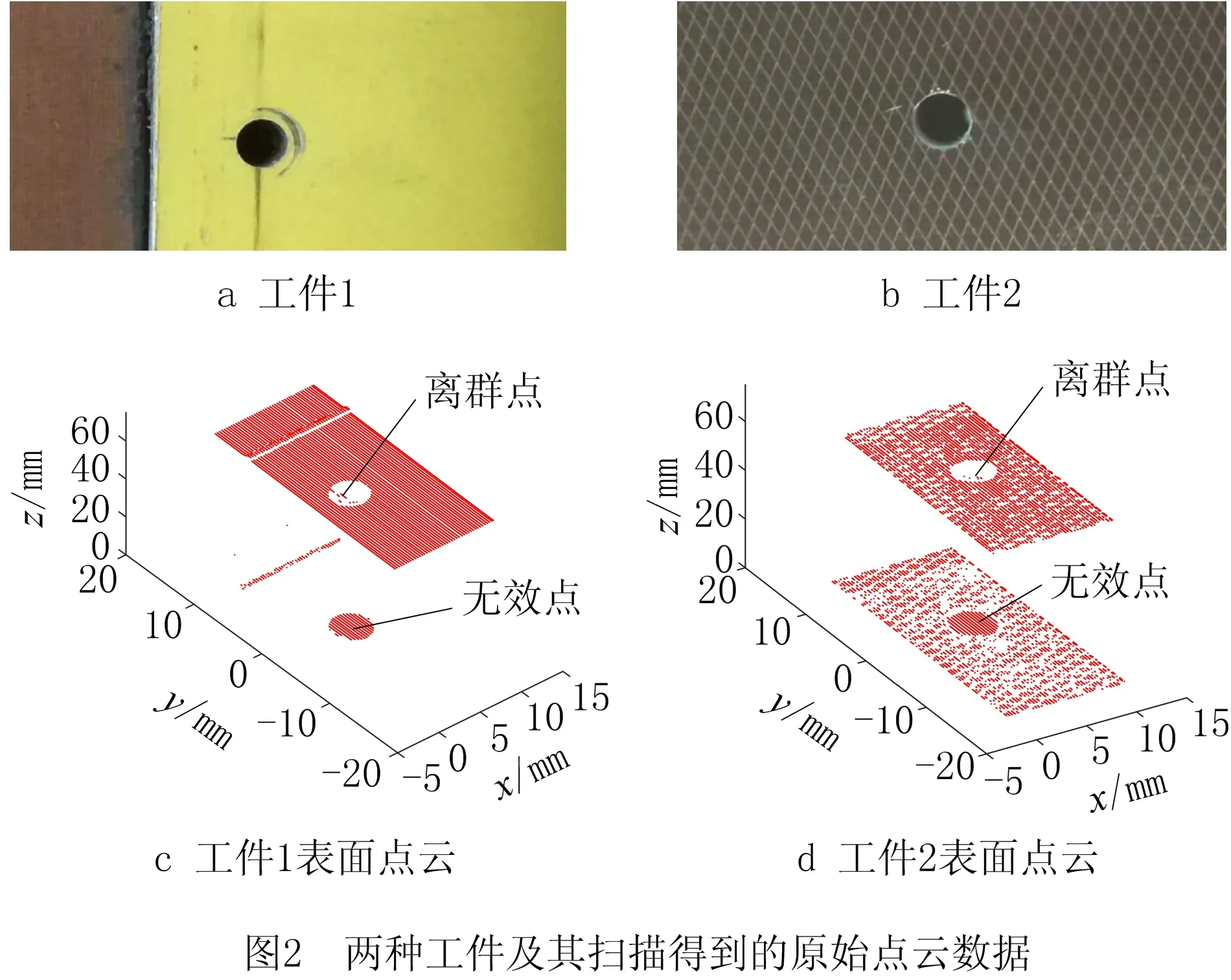
1.2 点云预处理
由于测得的点云数据密度高、数量大,且存在大量的无效点,针对这类点云数据首先要进行简化即去除无效点[12]。由图2c可以看出,工件1的表面点云较完整,仅在凹坑、裂缝处存在一些无效点,而工件2由于复合材料对激光的吸收率高,表面仅在铜网区域有反光,工件2的点云存在大面积的无效点,最终扫描得到的点云呈现网格状,如图2d所示。另外,由于孔边缘存在毛刺,以及基于三角法测量原理的2D激光轮廓仪的测量特点,不可避免地会扫描到孔的内壁部分区域,因此孔边缘会存在一些噪点和离群点,这些噪点会为孔的位置和法矢检测精度带来较大的影响。
为了提高孔的位置与法矢测量精度,必须先对点云进行预处理,以去除无效点和离群点。无效点的z坐标值默认为0,在实际测量时,无效点处虽然也存在y值,但此时的y值并非真实值,应将其去除。由于无效点的z坐标值都为0,根据该条件便可以将无效点的y值置零,去除无效点的方式如下:
(1)
采用中值滤波可以有效去除脉冲噪声,同时又能保留点云的边缘细节。基于中值滤波原理创建一个改进型中值滤波器F,滤波器内核B为矩形形状,核的尺寸为15×3。滤波器F的作用就是将点云S与核B进行卷积,对点云S的每个点进行逐一扫描。例如,当扫描到第i行、第j列的点P时,在点云S中取出以P点为中心的15×3邻域内的所有有效点(即z坐标值不为零的点),统计该邻域有效点的数量m,以及这些有效点的z坐标值的中值zm,然后求出Z0(i,j)与zm的差值的绝对值Zd=|Z0(i,j)-zm|。点P邻域内的有效点数量m的大小可用于判断点P是否为孤立点,在本例中,当m≤10时,该点判定为孤立点;Zd的大小反映了点P在Z方向上的离群程度,点P偏离群体越远,Zd的值越大,当Zd≥0.05mm时,该点判定为离群点。滤波器F的工作过程即为将孤立点和离群点的z值置零的过程,如下所示:
(2)
以工件1和工件2为例,去除无效点和离群点后的点云如图3所示。对比图2的原始点云与图3预处理后的点云可以看出,采用本文的预处理方法,可有效滤除基准孔边缘的噪点和离群点。

1.3 z坐标二值化
二值化是图像分割的一种方法,可以将灰度图像转换成二值图像。将大于某个临界灰度值的像素灰度设为灰度极大值,将小于这个值的像素灰度设为灰度极小值,从而实现二值化。
在执行孔扫描时,2D激光轮廓仪的激光发射方向与被测表面法向的夹角较小,即被测表面点云的z坐标值分布在一个较小范围内。可将点云的z坐标值进行二值化处理,即将空间三维点云投影到XY平面上。通过二值化处理,便将三维空间中的点云配准问题转化为二维平面的点云配准问题,降低了匹配复杂度,提高了计算效率。二值化处理方式如下:
(3)
以工件1和工件2为例,二值化后的点云如图4所示。

2 孔位检测算法
模板匹配是一种最原始、最基本的模式识别方法,研究某一特定对象物的图案在图像中的位置,进而识别对象物,这就是一个匹配问题[13]。它是图像处理中最基本、最常用的匹配方法。模板就是一副已知的小图像,而模板匹配就是在一副大图像中搜寻目标,已知该图中有要找的目标,且该目标同模板有相同的尺寸、方向和图像元素,通过一定的算法可以在图中找到目标,确定其坐标位置[14]。对z坐标值进行二值化处理后的点云,可以看作是一幅二值化后的平面图像,应用模板匹配的方法可以找出孔的位置。
2.1 孔模板的自适应构造
进行模板匹配之前,首先要构造孔的模板。在本例中,孔的形状为圆形,故构造的模板为外方内圆的形状,由m行n列的点构成,即模板尺寸为(m,n)。模板的自适应构造过程,即为确定模板尺寸(m,n)并构造出内圆外方形状的点云模板的过程。
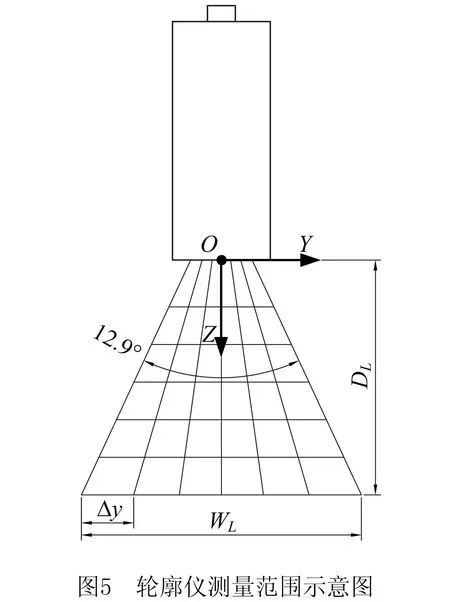
图5为2D激光轮廓仪测量范围示意图,2D激光轮廓仪的激光光束为发散式,发散角约为12.9°,由于激光线上采集点的数量为固定值row,测量距离DL越大,测量范围WL也越大,相邻两个采集点的间隔Δy也相应增大,即采集点越稀疏。对于同一尺寸的孔(本文例子中孔的直径为D=4 mm),测量距离DL越大,孔所包含的采集点的数量越少,孔模板的尺寸(m,n)也越小,在执行模板匹配之前,需要根据实测值计算出(m,n)。例如,在执行孔检测时,本文选用的轮廓仪Z方向量程为53 mm~78 mm,为使被测表面尽可能地落入测量量程内,将测量距离DL设定为65 mm。但由于存在工件安装误差和机器人运动误差,2D激光轮廓仪无法准确运动到距离被测表面65 mm的位置,测量距离难免存在一偏差,因此待测孔所包含的采集点数量也会相应地发生变化。为了构造出与基准孔实际尺寸相匹配的模板,需要知道X和Y方向上相邻采集点的距离Δx和Δy,其计算方法如下:
X方向:Δx=(X0L-X0R)/(col-1),
(4)
Y方向:Δy=(Y0U-Y0D)/(row-1)。
(5)
其中,X0L为第一列点云的x值;X0R为最后一列点云的x值;Y0U为第一行点云的非零y值的平均值;Y0D为最后一行点云的非零y值的平均值;col为点云的列数;row为点云的行数。则待测孔包含的点云的行数Hrow和列数Hcol分别为:
Hrow=D/Δy,
(6)
Hcol=D/Δx。
(7)
其中D为待测孔直径。
所构造的模板为外方内圆的形状,外边方形的尺寸略大于内圆的尺寸,外边方形的尺寸(m,n)即为模板的尺寸。模板的尺寸在保证能囊括孔的前提下,应尽可能的小,若模板尺寸设定过大,测量曲面上的孔时,与之匹配位置的曲面已经不能近似作为平面处理,后续进行法向计算时精度将降低。本文根据点云的密度,将模板尺寸设定为:
m=Hrow+6,
(8)
n=Hcol+2。
(9)
为方便处理,将模板的尺寸调整为奇数,调整方法如下:

(10)
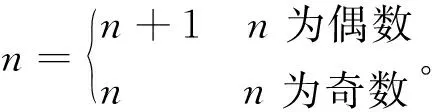
(11)
当被测表面为平面,且与激光发射方向垂直时,被测表面上的圆孔经过z坐标二值化后仍然是圆形;而当被测表面为平面但与激光发射方向不垂直时,或者被测表面为曲面时,被测表面上的圆孔经过z坐标二值化后可能变为椭圆或者不规则的椭圆,如图6所示。为了构造与之匹配的孔模板,需要先计算出被测表面的法向,根据该法向数值在三维空间中构造孔模板,该孔模板与被测表面平行。构造好三维孔模板后,再将孔模板进行z坐标二值化处理,转化为二维的孔模板,此时的孔模板便能够适应倾斜平面(倾斜角度小于60°)和曲面(曲率半径至少为待测孔半径的10倍,且待测孔法向与激光的夹角小于45°)的测量要求。考虑到实际应用中,轮廓仪激光束与被测面法向的最大夹角一般要求小于45°,本文的算法已经可以满足实际需求。
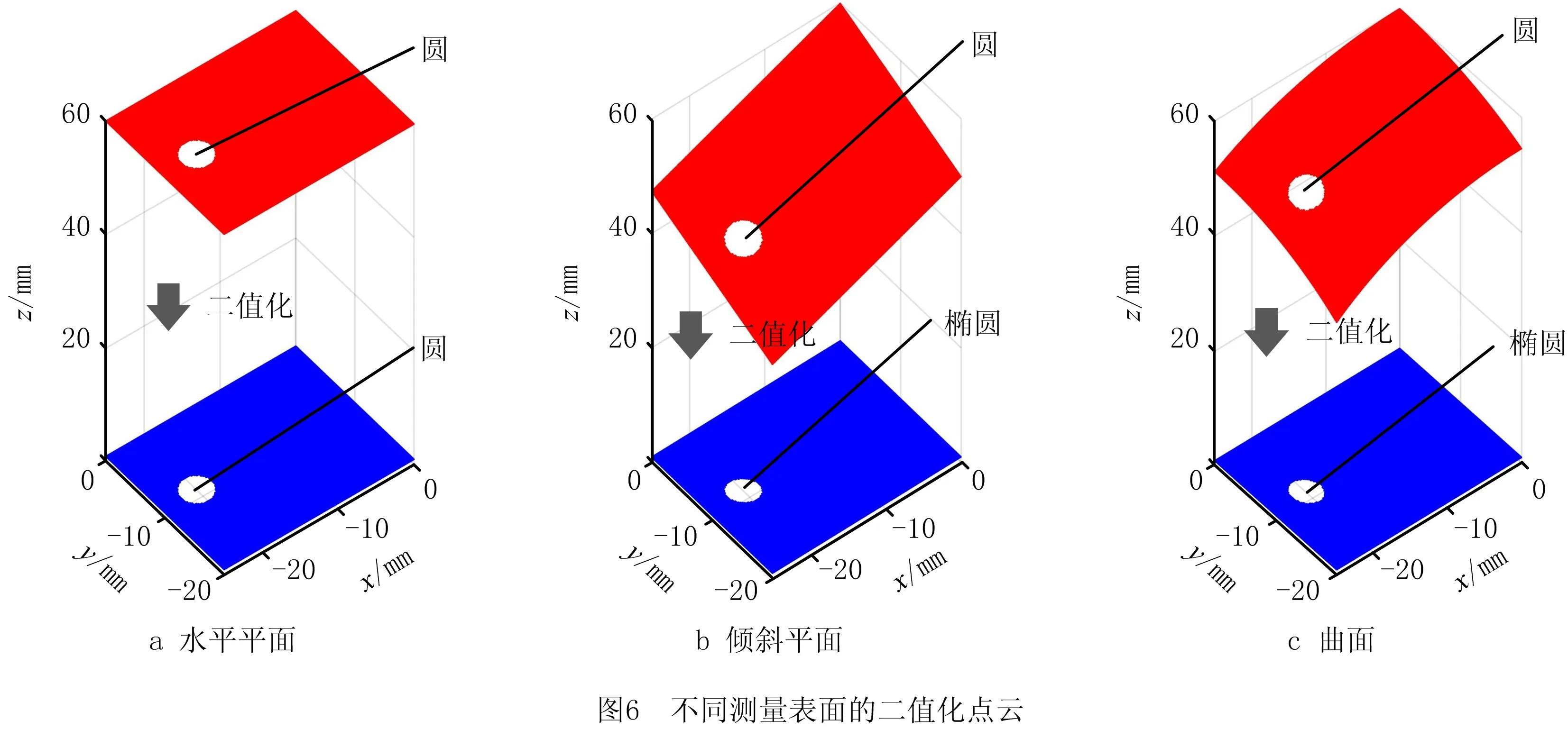
采用最小二乘法或者SVD法拟合平面即可求出被测表面的法向。由于参与拟合点云的数量较多,导致计算量偏大,需要先对点云进行降采样。将点云沿X、Y方向均分为10等分,利用拉丁超立方采样,既可以保证采样的随机性,又能避免采样点过于聚集的问题。采样完成后,利用采样点拟合出平面并计算该平面的单位法向N(a0,b0,c0),并构造m×n三维平面状点云作为模板,该模板的法向为N(a0,b0,c0)。然后去除离模板中心点的距离小于基准孔半径的点,最后将该三维孔模板进行z坐标二值化处理,转化为二维的孔模板。以工件2为例分别扫描水平平面、倾斜平面和曲面上的一个待测孔,根据上述方法自适应构造的待测孔的模板T(m,n)如图7所示,模板尺寸(m,n)分别为(59,17)、(45,17)和(53,17)。可见,在不同倾斜表面上相同尺寸和形状的待测孔,构造出来的孔模板的尺寸和形状并不相同,待测孔所处表面的斜度越大,孔模板的尺寸越小,且孔的形状越扁平。

2.2 模板匹配
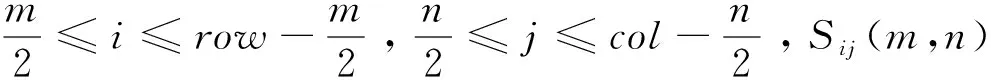
其中E(i,j)最小值处即为匹配到的目标孔的位置。模板越大,匹配速度越慢;否则,匹配速度越快。以工件2为例,待测孔的匹配结果如图8b所示,匹配率K越高,说明匹配的可信度越高。模板匹配的匹配率K:
(13)

2.3 ROI孔特征判别
由于待测孔边缘和表面难免存在一些缺陷,扫描得到的待测孔点云不可能与模板100%匹配,通常需要设定一个模板匹配率阈值Kt。在执行模板匹配过程中,首先找出匹配率K最高的位置,然后判断K是否大于所设定的模板匹配率阈值Kt,只有满足K>Kt时才认为检测到了孔特征。在实际扫描测量时,如果待测孔的表面质量很稳定,可以将阈值Kt设定为90%以上,从而降低误识别的可能性。但在本例中,工件2的表面点云存在大量瑕疵,孔特征匹配率K≈60%~80%,非孔特征匹配率K≈0%~65%,孔特征与非孔特征的界线模糊,若模板匹配率阈值Kt设置过大,则孔特征容易被误判为非孔特征;否则,则容易将非孔特征误判为孔特征。以工件2为例,将Kt设定为70%时,孔特征的误判率高达35%,因此无法单纯地通过设定模板匹配率阈值的方法判断待测区域是否有孔特征。
分析孔特征与非孔特征的点云特点可以发现,孔特征的点云在中心圆形区域内为空集,而非孔特征的点云在中心圆形区域内存在采集点,将待测孔模板T(m,n)的中心圆形区域设定为感兴趣区域(ROI),计算ROI的匹配率Kr。以工件2为例,孔特征的ROI匹配率Kr≈90%~100%,非孔特征的ROI匹配率Kr≈0%~45%,孔特征和非孔特征的ROI匹配率Kr有明显的区别。通过设定ROI匹配率的阈值Krt可有效地判别孔特征,将模板匹配率阈值Kt与ROI匹配率的阈值Krt同时作为孔特征的判别条件,可准确地检测出孔特征。以工件2为例,Kt设定为60%,Krt设定为85%,可将孔特征的误判率降低到1%以下。
2.4 待测孔的位置与法矢计算
模板匹配只是找出了待测孔在被测面点云上所处的序列位置(i,j),待测孔的具体空间坐标值C(xC,yC,zC)还是个未知数。匹配位置下的子图Sij(m,n)中心位置的坐标值即为孔中心的坐标值,但由于待测孔内部不存在采集点数据,即匹配位置(i,j)处并不存在点云,无法直接读出(i,j)处的坐标,需通过子图Sij(m,n)间接计算出圆心的坐标,将子图Sij(m,n)上的所有点的坐标值的平均值作为圆心的坐标C(xC,yC,zC):
(14)
式中N为子图Sij(m,n)包含的有效采集点的数量。
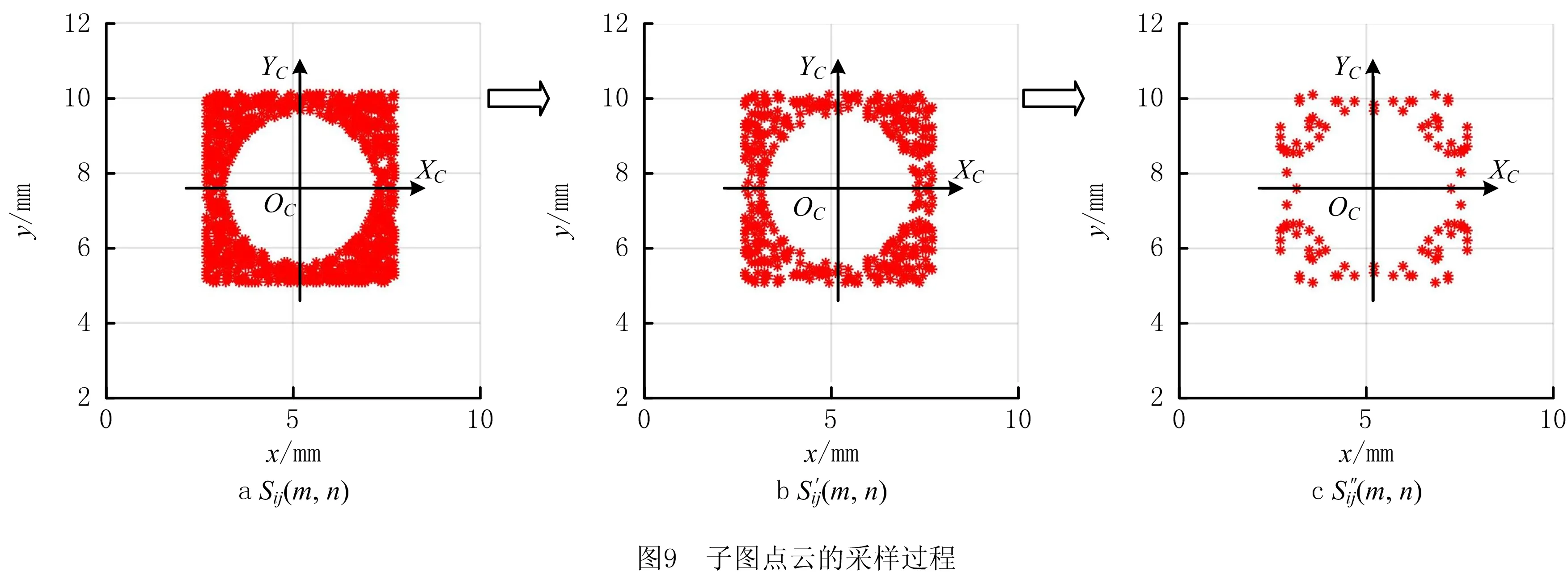
当遇到不理想的网格状点云时,匹配位置下的子图Sij(m,n)存在点云残缺的情况,按式(14)计算出来的圆心坐标将会向点云较多的方向偏移,导致较大的测量误差,因此,需要对该方法作进一步优化。如图9所示,首先以子图Sij(m,n)的中心为原点建立一个坐标系OC-XCYCZC,方向与点云的坐标系方向一致;接着以XC轴为对称轴对子图Sij(m,n)中的点进行筛选,只有关于XC轴对称的一对点能够保留,利用该条件得到新的子图S′ij(m,n);然后以YC轴为对称轴对子图S′ij(m,n)中的点进行筛选,只有关于YC轴对称的点云对能够保留,利用该条件得到新的子图S″ij(m,n);最后再利用式(14)计算出圆心坐标C(xC,yC,zC)。经过筛选后,子图S″ij(m,n)中的点云呈中心对称分布,对称中心即为圆心,因此可以利用式(14)准确计算出圆心坐标。
被测表面可能为平面,也可能为曲面,但由于孔尺寸较小,曲面曲率较小,可将孔邻域的曲面近似看作平面。采用SVD分解可利用子图Sij(m,n)上的点拟合出一个平面,协方差矩阵的SVD变换中,最小奇异值对应的奇异向量就是该平面的单位法向向量M(a,b,c)。以该平面的单位法向向量近似代替待测孔的法矢。
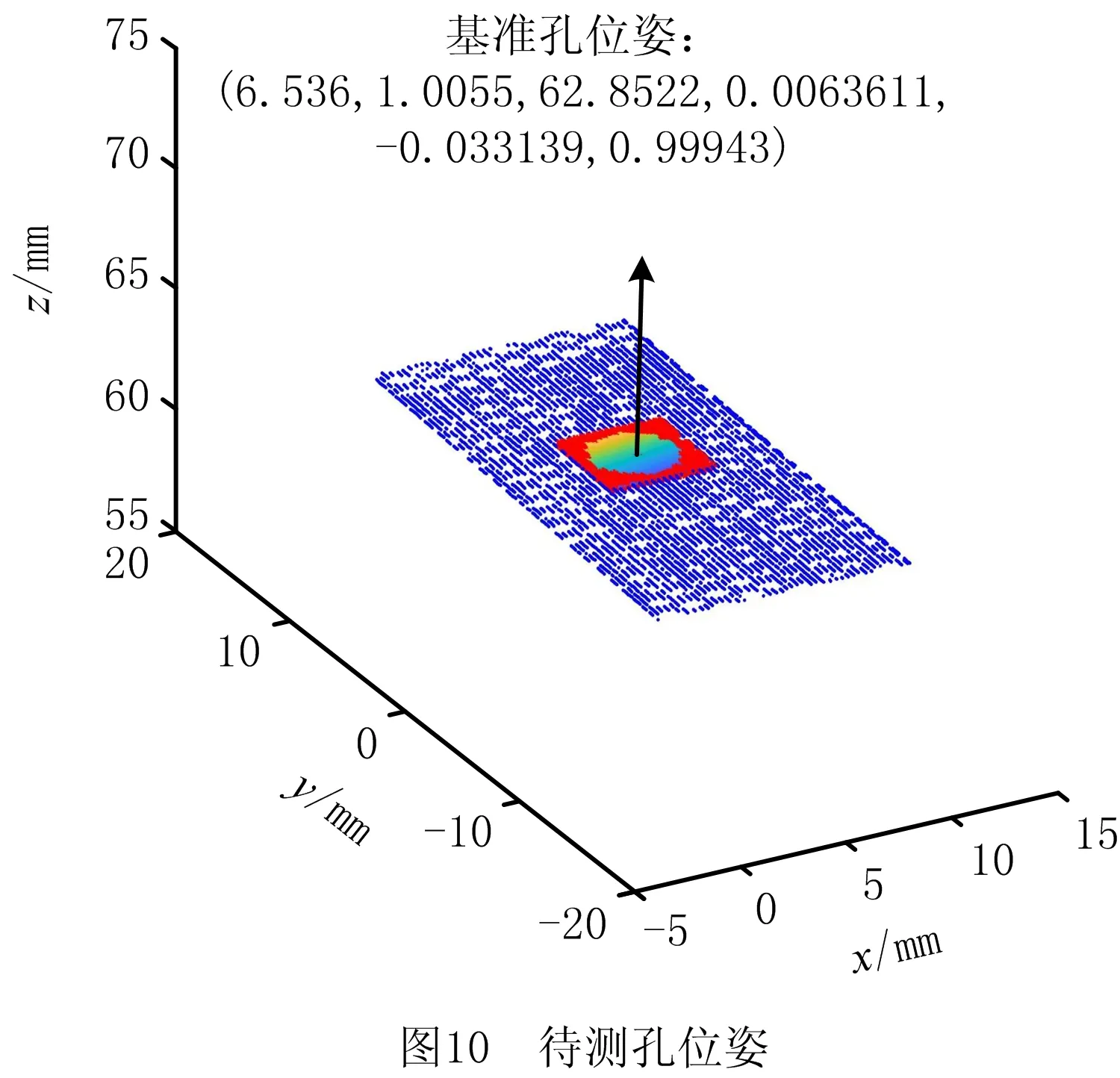
综上所述,待测孔在2D激光轮廓仪坐标系下的位姿为P(xC,yC,zC,a,b,c),以工件2为例,计算得到的待测孔位姿如图10所示。
3 实验对比与分析

3.1 实验平台
为验证本文提出的孔位与法矢检测算法的可行性和测量精度,搭建了孔位检测实验平台,如图11所示。平台由2D激光轮廓仪(也称为外轮廓传感器)和西门子伺服电机等组成,其中,2D激光轮廓仪的型号为米铱scanCONTROL 2900-25,激光线可采集320个点。西门子伺服电机与精密丝杠组成的直线运动机构,其定位精度可达5 μm,因此,在本实验中,运动机构的精度对孔位测量结果的影响可以忽略不计。然而,伺服电机编码器的采样周期直接影响X方向上的孔位测量精度,采样周期越短,点云越密集,相应的测量精度越高。但随着点云数量的增多,计算量将成倍增加,导致计算效率下降,因此在实际应用时,应根据测量精度需求合理设置采样周期。实验中,设置伺服电机的速度V=100 mm/min,2D激光轮廓仪的采样周期设置为T=0.15 s,每间隔0.15 s同时采集2D激光轮廓仪的数值和伺服电机编码器的数值,通过编码器的数值可计算得到X方向的位移,最终可得到3个row×col的矩阵X0、Y0、Z0(其中row为矩阵行数,即每条线轮廓采集的点数;col为矩阵列数,即采样次数),分别记录点云在X、Y、Z三个方向的位置。
3.2 孔位检测精度实验
在工件2上钻出2列10行共20个孔,每行的2个孔为一组,孔的直径为4 mm,孔间距为10 mm,如图12所示。首先用中心距游标卡尺测量出每一组2个孔的中心距L。接着将工件2固定在实验平台上,分别对每一行孔进行扫描,可得到10组点云数据Ai(i=1,2,…,10)。然后在工件2的表面喷涂显影剂(喷涂显影剂可有效改善工件表面光泽,扫描得到的点云完整无瑕疵),并分别对每一行孔进行扫描,可得到10组点云数据Bi(i=1,2,…,10)。最后,采用传统的基于边缘检测的孔位检测算法和本文提出的基于模板匹配的孔位检测算法,对扫描得到的点云进行孔位检测并计算2个孔的中心距。实验结果如表1所示,其中L为用中心距游标卡尺测量出的孔中心距,L1为采用传统的基于边缘检测的孔位检测算法测量的孔中心距,L2为采用本文提出的基于模板匹配的孔位检测算法测量的孔中心距。L1、L2与L的差值即为孔位检测误差,如图13所示,其中ΔLH1为喷涂显影剂后采用传统的基于边缘检测的孔位检测算法的检测误差,ΔLQ2为喷涂显影剂前采用基于模板匹配的孔位检测算法的检测误差,ΔLH2为喷涂显影剂后采用基于模板匹配的孔位检测算法的检测误差,各检测误差的流计数据如表2所示。


表1 孔中心距的测量结果

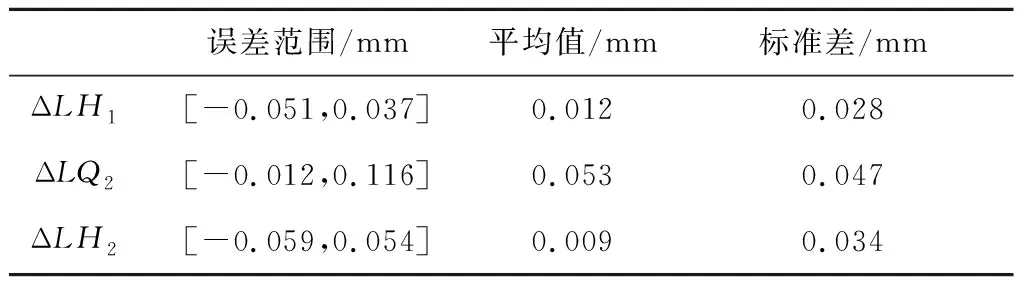
表2 两种孔位检测算法的测量结果统计数据
3.3 实验结果分析
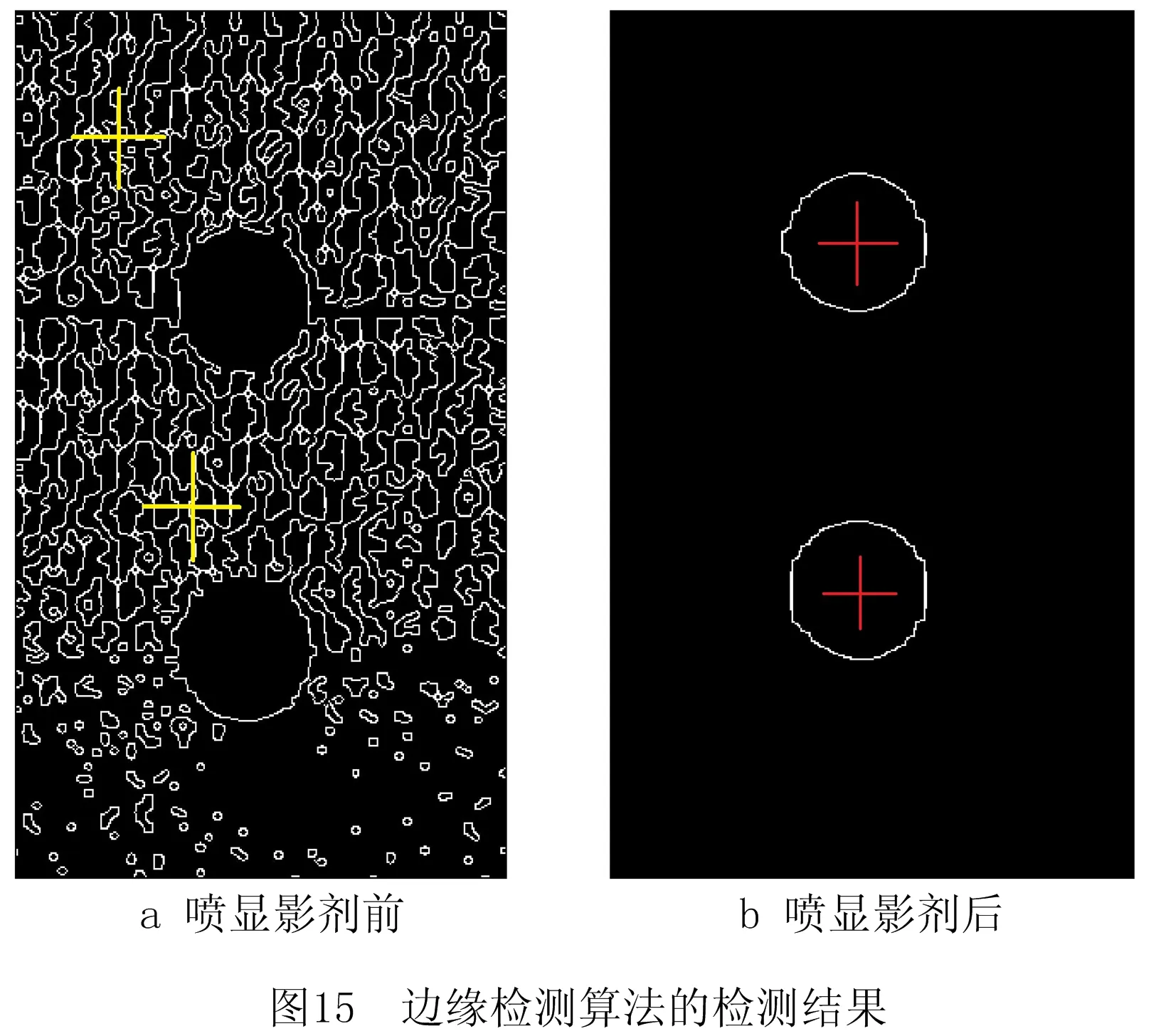
喷涂显影剂前后扫描得到的点云如图14所示。可以看出,喷涂显影剂前,工件2表面扫描得到的点云存在大量缺陷,整体呈现网格状。传统边缘检测算法利用canny算子进行边缘检测,并采用霍夫变换找出圆轮廓。对于网格状的点云,由于边缘检测检出了大量的网格轮廓边缘,霍夫变换找出的圆心位置已完全偏离了实际位置,如图15a所示,因此该算法不再适用,中心距的测量实验结果也没有实际的意义。而喷涂显影剂后,点云较理想,基于边缘检测的孔位检测算法可以识别出孔边缘从而进行孔位计算,如图15b所示。

在飞机部件自动钻铆中,基准孔检测精度要求在±0.5mm以内,从实验结果可以得到如下信息:
(1)通过比较表1中两种算法对于喷涂显影剂前后的孔位检测成功率,可以看出,喷涂显影剂前,基于边缘检测的孔位检测算法对于孔的识别成功率为0%,说明基于边缘检测的孔位检测算法只适用于很理想的点云,鲁棒性较差;而本文提出的基于模板匹配的孔位检测算法在喷涂显影剂前后的检测成功率均为100%,说明本文的算法具有较强的鲁棒性。
(2)通过比较喷涂显影剂后两种孔位检测算法的测量误差ΔLH1和ΔLH2,可以看出两种算法的测量误差接近,证明了对于理想的点云,采用基于模板匹配的算法与采用基于边缘检测的算法测量精度相当,且均满足飞机部件装配精度要求。
(3)通过比较喷涂显影剂前后采用基于模板匹配算法的测量误差ΔLQ2和ΔLH2,可以看出尽管未喷涂显影剂时测量精度有所降低,但依然可以满足飞机部件的装配精度要求,意味着采用本文提出的基于模板匹配的孔位检测算法之后,可以省去喷涂显影剂这个工艺步骤,进而提高了飞机装配的效率。
4 结束语
针对高反光金属、强吸光复合材料等不理想表面的孔位与法矢检测困难的问题,本文提出一种基于模板匹配的孔位与法矢检测算法,将图像处理中的模板匹配方法应用于三维点云中孔位与法矢的检测,鲁棒性较强。经实验验证,算法可有效检测出不理想表面的孔位和法矢,对于不理想表面的孔位检测精度达0.12 mm,满足飞机部件装配要求;另外,采用本文提出的基于模板匹配的孔位与法矢检测算法之后,可以省去喷涂显影剂这个工艺步骤,进而缩短了产品的生产周期,在产品的自动化制造装配过程中具有良好的应用前景。未来将针对复杂工况下的孔位识别进行研究,如识别的孔为沉头孔或抽芯铆钉,扩展自动钻铆系统孔位识别的应用场景,提升系统的鲁棒性和稳定性。
