基于二维二元语义和前景理论的改进FMEA法
2022-01-07孙延浩袁志明
孙延浩,张 琦,袁志明, 李 智
(1.中国铁道科学研究院 研究生部,北京 100081;2.中国铁道科学研究院集团有限公司 通信信号研究所,北京 100081)
0 引言
故障模式及影响分析(Failure Mode and Effects Analysis,FMEA)是一种分析系统潜在故障或失效模式,及其对系统造成影响的方法[1]。该方法通过分析故障模式的发生概率( Occurren-ce,O) 、严重程度( Severity,S) 和检测难易程度( Detection,D)3个风险因子来获取风险优先数(Risk Priority Number,RPN),并依照RPN的大小进行风险排序。FMEA方法由于快速、高效、简单而被广泛应用于各种领域,然而传统FMEA法在实际应用中却存在着一些问题:①风险因子评估具有很强的模糊性和不确定性,难以用精确数字表征;②没有考虑风险因子的权重;③RPN计算只是简单地通过风险因子的乘积来获取,造成RPN对故障模式的评价结果过于敏感,使得风险排序相对粗糙。
为克服上述缺陷,不少专家学者对FMEA方法进行了改进。针对问题①,众多学者将模糊集引入FMEA方法中,文献[2]运用三角模糊数来刻画风险因子评估中的模糊性;在此基础上,文献[3]又结合软集的优点,提出三角模糊软集的评价方法;文献[4]提出一种基于犹豫模糊集的评价方法,该方法在表示专家评估信息时,更好地传达了专家在评估时的犹豫性;文献[5]采用直觉模糊集来评估风险因子,并利用直觉模糊集成算子来对评估信息进行集结,进而对故障模式进行风险排序;为了更好地减少评估信息集结中的损失,文献[6-7]运用二元语义作为评估语言,二元语义既能克服评估信息的模糊性,又便于集结,降低了风险排序的难度。上述方法对于风险因子评估中的模糊性和不确定性都有较好的处理,但大部分研究对于模糊性和不确定性的处理基本集中在评价语言本身,如犹豫模糊集,它允许专家采用多个评语来进行描述,但该方法在后期数据处理上容易丢失部分决策信息,以(s1,s2,s3,s4)和(s1,s3,s4)为例,在进行计算时,一般将两者均转换为区间数[s1,s4],但前者包含的信息多于后者,这样的转换导致信息丢失[8]。
对于问题②,为降低计算难度,文献[9]和文献[10-11]分别采用层次分析法(Analytic Hierarchy Process, AHP)和改进的AHP来计算风险因子的权重,但AHP对专家的知识和经验度依赖较大,导致权重的计算结果具有很大的主观性,这极大地影响了故障模式的风险排序的准确性。因此,目前采用综合赋权法的研究较多,综合赋权法同时考虑风险因子的主客观权重,相较于单方面因素的赋权法,权重计算更为准确,但由于大部分改进方法基本将FMEA视为一种群决策的行为,这就导致专家和风险因子权重出现了耦合性,两者相互制约和影响,为了获取风险因子权重,大部分研究直接赋予专家权重,这降低了风险排序的准确度。
针对问题③,常见的优劣解距离法(Technique for Order Preference by Similarity to an Ideal Solution, TOPSIS)[2]、折衷排序法(VlseKriterijumska Optimizacija I Kompromisno Resenje, VIKOR)[12]、决策实验和评价实验室法(Decision-making Trial and Evaluation Laboratory, DEMATEL)[13]和证据推理[14]等多属性决策方法多被广泛应用于FMEA中,但是这些决策方法一般较为单一,排序的鲁棒性不强,同时大部分研究方法基本都是假定决策者完全理性,事实上决策者在面临决策时总是有一种趋利避害的心理趋势,常用的多属性决策方法对于决策者在面对决策时的心理特征刻画不足,导致FMEA法在实际运用中具有较大的局限性。
可以看出,对于FMEA的改进还有一些需要优化的地方,为克服以上不足,本文在前期既有研究的基础上,采用二维二元语义来描述风险因子O、S和D的信息,二维语言变量[15]是近几年发展起来的一种新型模糊语言变量,它在传统模糊语言信息的基础上增加一维反映专家评价确定程度的第Ⅱ维语言信息,二维二元语义在表达信息上更为全面,更符合现实决策情况,二元语义[16]作为一种评价语言具有灵活性强、信息丢失少的优点,采用二维二元语义评价风险因子O、S和D,不仅可以有效表征评价的模糊性和不确定性,还能尽可能减小信息丢失。对于风险因子的权重,考虑专家和风险因子权重之间的耦合性,本文首先获取专家权重,再在此基础上计算风险因子权重。在进行风险排序的过程中,由于决策者往往是非完全理性,在面对得失时,经常表现出不同的心态,考虑到前景理论可以很好地反映不确定环境下决策者的心理特征[17],将前景理论和二维二元语义相结合,提出一种基于二维二元语义和前景理论的改进FMEA法。最后将本文所提改进FMEA法用于高速铁路 (简称高铁)信号系统的集成电路板回流焊接风险评估,验证了该方法的有效性。
1 二维二元语义表示模型
二维二元语义是对传统二元语义的一种拓展,在传统二元语义的基础上,增加一个维度来描述专家自己对评价信息的确定程度,以更为全面的形式来表述决策者意见。下面给出二维二元语义的相关概念。
1.1 二元语义
定义1[16]设S=(si|i=0,1,2,…,g)为一个自然语言术语集,β为S的下表集成值,即为S的符号集成运算值,β∈[0,g]为符号集成运算值,设i=round(β)(“round”是四舍五入取整运算),α=β-i,使得i∈[0,g],α∈[-0.5,0.5),称α为sp的符号平移。则可通过函数Δ得到β的二元语义:
(1)
定义2[16]设S=(si|i=0,1,2,…,g)为一个自然语言术语集,(si,α)为S上的一个二元语义,则存在逆函数Δ-1将二元语义转换成相应的数值β∈[0,g],即
(2)
定义3[18]设S=(si|i=0,1,2,…,g)是一个自然语言术语集,(si,α)为S上的一个二元语义,则其得分函数为:
(3)
式中g为二元语义的粒度。二元语义的大小可以根据得分函数来进行判断,得分函数越大,则二元语义越优。
1.2 二维二元语义集
定义4[15]设S=(si|i=1,2,…,g)和H=(hp|p=0,1,2,…,l)为两组自然语言术语集,Si=(si,αi)和Hp=(hp,φp)分别为S和H上的两个二元语义,则[(si,αi),(hp,φp)]表示为一个二维二元语义。特别地,当αi=φp=0时,[(si,αi),(hp,φp)]简记为[si,hp]。
定义5[19]设Sip=[(si,αi),(hp,φp)]为一个二维二元语义,则其期望值为:
(4)
期望值常用来分辨二维二元语义的大小,文献[19]认为期望值越大,则二维二元语义越优。但期望值实际上只是得分函数简单的相乘,无法体现两个维度的重要性。例如[(s2,-0.2),(h2,-0.4)]、[(s2,0.4),(h1,0.2)]、[(s4,-0.4),(s1,-0.2)]和[(s1,0.2),(s2,0.4)],假定第Ⅰ维二元语义粒度为6,第Ⅱ维二元语义粒度为4,其期望值均为0.12。若按期望值进行比较,四者是等优的,显然不符合逻辑。文献[20]提出一种比较方法,但是该方法会出现二维二元语义无法比较的情形,考虑到不同维度之间的差异,为克服以上缺点。本文提出一种新的比较方法。
为了能更好地说明比较方法,本文先从几何角度来说明二维二元语义。如图1所示令η为维度比例系数,横坐标表示第Ⅰ维二元语义,坐标长度表示其粒度与η的乘积,纵坐标表示第Ⅱ维二元语义,坐标长度表示其粒度与(1-η)的乘积,若0.5<η≤1,表明决策者更为重视第Ⅰ维的决策信息,若0≤η≤0.5,则表明决策者更为重视第Ⅱ维的决策信息,图1中A点坐标表示二维二元语义[(si,αi),(hp,φp)],由于αi=φp=0,A点简记为[(si,hp)];B点坐标表示二维二元语义[(sj,αj),(hq,φq)]。
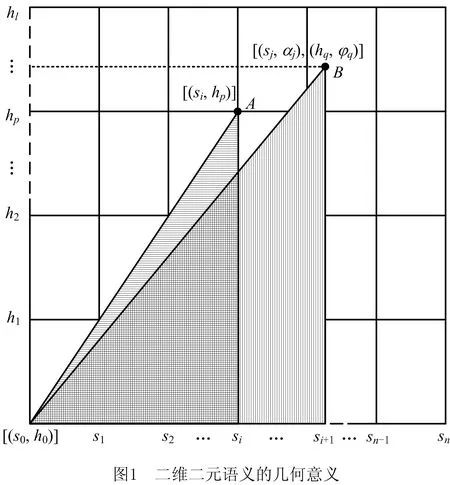
设Sip=[(si,αi),(hp,φp)]为一个二维二元语义,对其进行标准化后表示为:
N(Sip)=[ηT(si,αi),(1-η)T(hp,φp)]
=[ηx,(1-η)y]。
(5)
式中:x=T(si,αi),y=T(hp,φp)。
为了使分函数的区分度尽可能高,本文采用面积与周长之和表征二维二元语义的得分函数。
设Sip=[(si,αi),(hp,φp)]为一个二维二元语义,其得分函数为
T(Sip)=η(1-η)xy+ηx+(1-η)y+
(6)
为简化计算,对式(6)中的面积和周长作一些改变,由于在乘法运算中维度系数不再发挥作用,去掉面积中的维度系数,对于周长,由于所构成三角形为直角三角形,只计算横、纵坐标之和。将得分函数简化如下:
T(Sip)=xy+ηx+(1-η)y,x,y≥0。
(7)
本文采用得分函数对两个二维二元语义进行比较,设Sip=[(si,αi),(hp,φp)]和Sjq=[(sj,αj),(hq,φq)]为两个二维二元语义,则两者的比较规则如下:
若T(Sip)>T(Sjq),则Sip≻Sjq;
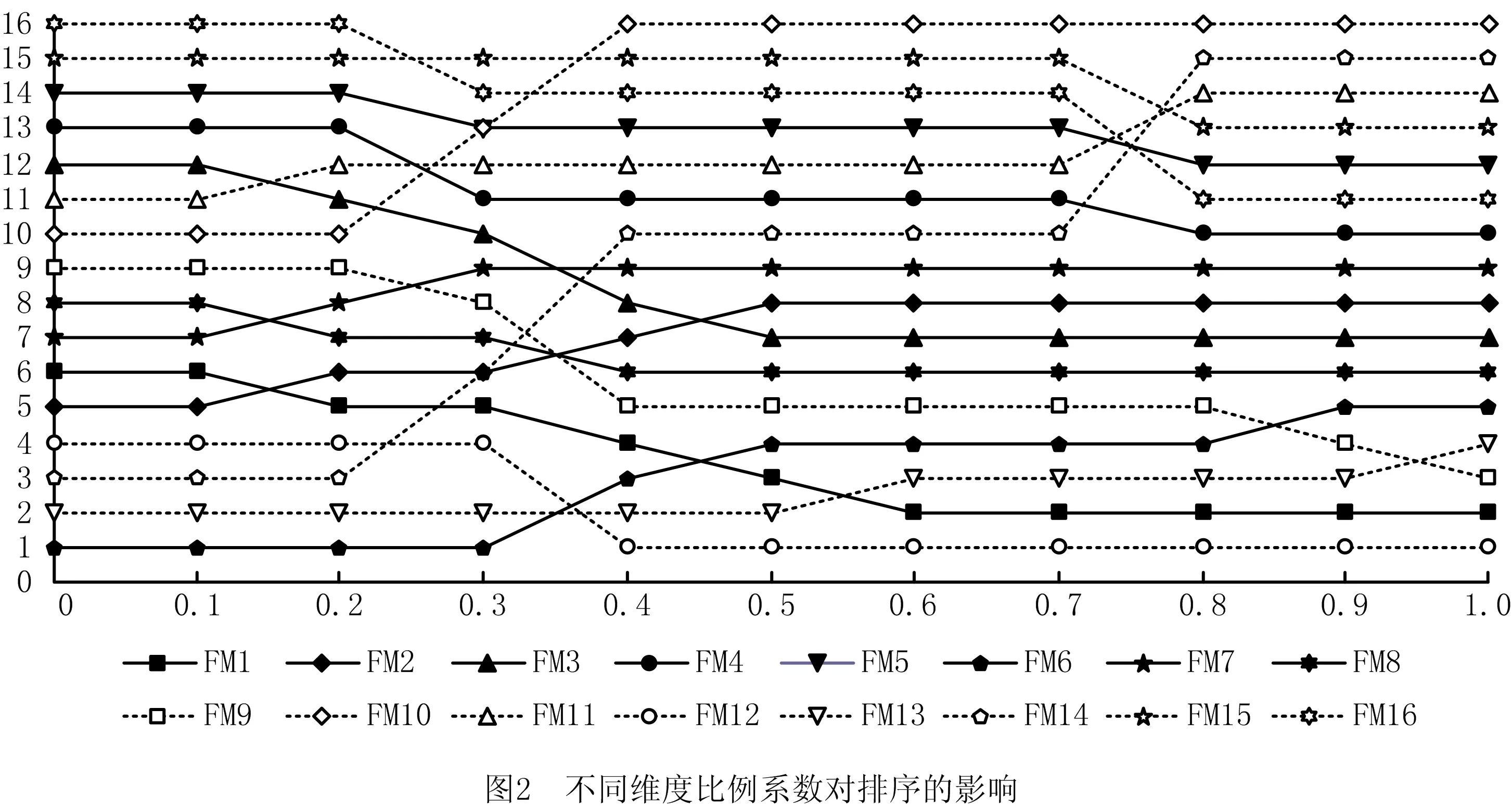
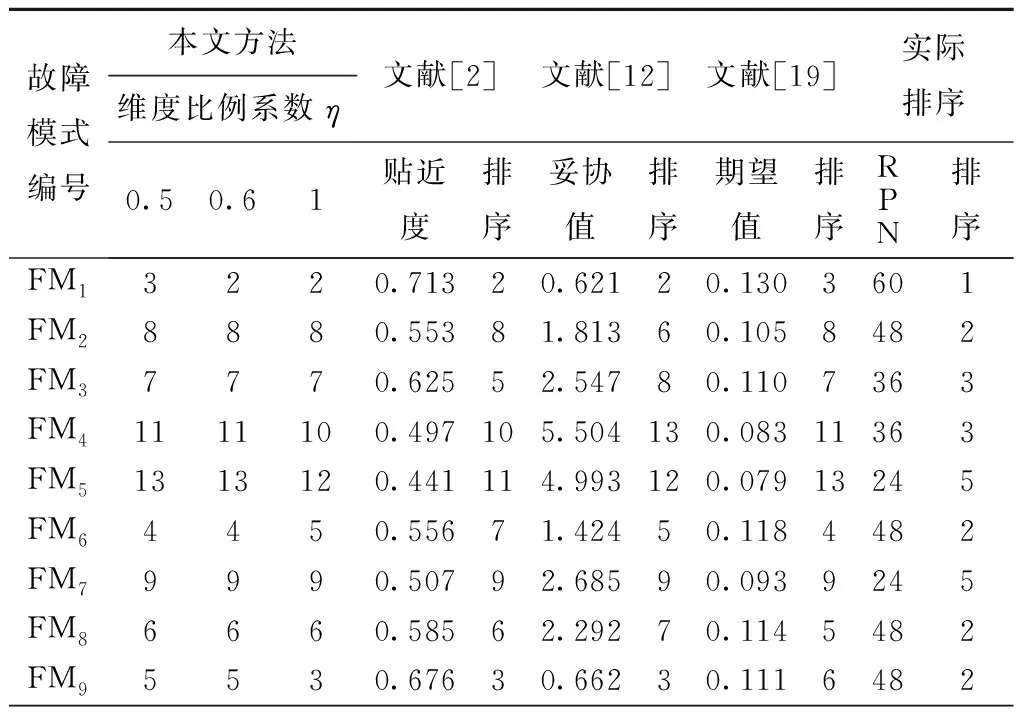
若T(Sip) 若T(Sip)=T(Sjq),则Sip~Sjq。 定义6设Sip=[(si,αi),(hp,φp)]和Sjq=[(sj,αj),(hq,φq)]为两个二维二元语义,分别对应于坐标上的A点和B点,则两者之间的距离为: (8) (9) 群决策中个体决策不论以哪种方法集结,都会涉及到属性(风险因子)和专家的权重,风险因子权重和专家权重互相耦合,相互影响。专家作为具有主观能动性的个体,其权重相对于风险因子权重,具有较大的灵活性,由于专家专业知识和经验度有差异,并不是每个专家对所有属性都熟悉了解,因此不同风险因子下,专家的权重是变化的[21]。风险因子作为故障模式的固有属性,其属性权重应该较为稳定,它不应随专家的不同而变化。基于此,本文先获取专家权重,再在此基础上计算风险因子权重。 二维二元语义的第Ⅱ维度是专家对自己评测的一种主观评价,一个专家的评价越确定,则应赋予他的权重越高。因此,本文用它来表征专家的主观权重。专家的主观权重公式为: (10) 群决策反映的是专家组集体协商最终达成共识的过程,它反映专家意见的妥协,最终结果应当趋于一致,若个体与群决策差异大越,说明他与群体的共同意愿越远,则应赋予该专家较小的权重,从而削弱其影响。香农在信息论中指出熵可以用来表示系统紊乱程度,熵越大系统越紊乱,否则系统越稳定,越趋于一致。 当系统可能处于几种不同状态, 每种状态出现的概率为pi(i=1,2,…,m)时, 系统的熵为: 当系统所处的状态为等概率状态时,此时系统最紊乱,熵值最大。即 E(f1,f2,…,fm)≤E(1/m,1/m,…,1/m)=ln(m)。 (11) (12) 求解上述模型,得到专家Dk在风险因子Cj下的客观权重为: (13) 证明构建拉格朗日函数: 最后,对专家的主、客观权重进行合成,得到专家的综合权重,即 (14) 式中ρ(0≤ρ≤1)为偏好系数,ρ越接近1,则综合权重越倾向于主观权重;ρ越接近0,则综合权重越倾向于客观权重。 专家权重的计算过程中,采用距离来表示信息熵的大小,在属性计算过程中,本文采用评价分值来表示信息熵,在群决策中,专家对故障模式的风险因子进行评价,通过计算各故障模式的风险因子得分对故障模式进行评价排序,不同的风险因子对故障模式具有不同的重要度,风险因子的重要度可以用属性的熵来衡量。 通过式(11)和熵的极值性可以看出[22],若风险因子Cj在不同方案上的评价值越接近,风险因子Cj的熵值越大,说明风险因子Cj在各方案上的取值与该风险因子均值之间的差异度越小,越接近最优值,则该属性在决策中起的作用越小,其权重越小。各属性熵值 (15) (16) 传统FMEA法不关心专家在评估风险因子时的心理因素,默认为专家在决策时是完全理性的,但在实际决策过程中,决策者通常会表现出有限理性的心理特征。前景理论[17]认为决策者在进行不确定决策过程中,决策结果与决策者的主观偏好具有一定的关系,该理论认为个人基于参考点的不同,会有不同的风险态度,在参考点上,人们有时会更加重视结果与预期的差距。而不是结果本身。因此,参考点的选择是前景理论的关键,受TOPSIS方法的启发,根据式(4)比较两个二维二元语义的大小,进而确定正、负理想方案: (17) 由于风险因子均属于成本型属性,则 (18) 由各评价值到参考点的距离,得出故障模式的前景决策矩阵: (19) (20) 群体决策关于方案FMi的正、负前景值为 (21) 方案FMi的综合前景值为 (22) 最终根据各方案的综合前景值进行排序。 高铁信号系统是我国高速列车安全、正点和高效运行的重要保障。其设备一旦出现故障,轻则造成运输效率下降,重则造成重大行车安全事故。相较于普速铁路时代,如今的信号控制技术是以集成电路控制为核心,对于其中的核心硬件集成电路来说,其硬件的可靠性尤为重要。信号设备厂商在设备生产时需要大量的裸板、芯片等元器件进行焊接作业。如某高铁信号设备项目中需要大量的集成电路板,集成制造商在采购裸板、芯片等元器件结束后需要进行一系列的生产活动,其中主要是焊接作业,包括波峰焊、回流焊等,回流焊主要针对贴片元器件进行作业,将元器件可靠地焊接到印制电路板(Printed Circuit Board,PCB)上,不但需要专业回流焊机进行自动化焊接,而且部分辅助工作作业也需要人为参与,整个过程对环境、人、机器有较高要求,各个因素会对最终的焊接质量起到至关重要的作用。为了追求更高的产品质量,该设备集成制造商邀请3位不同经验和知识度的专家组成FMEA专家组,对回流焊接过程中存在的16种潜在故障模式(如表1)进行风险分析排序,专家组对上述潜在故障模式下的O、S、D进行评价。第1维评语集选用言术语集S={s0(极低),s1(很低),s2(低),s3(稍低),s4(一般),s5(稍高),s6(高),s7(很高),s8(极高)},第2维评语集选用术语集H={h0(不确定),h1(基本不确定),h2(不太确定),h3(一般),h4(比较确定),h5(基本确定),h6(十分确定)},3位专家给出的评估信息如表2。 表1 回流焊接过程中存在的16种潜在故障模式 表2 3位专家给出的评价矩阵 对高铁信号设备的集成电路板回流焊接进行风险分析,其步骤如下: 步骤1文献[24-25]认为在实际中第Ⅱ维评价信息重要度小于第Ⅰ维评价信息。基于此,设本文维度比例系数η为0.6。根据式(10)~式(14)获取专家的权重,为不失一般性,将主客观权重系数ρ取0.5,得到不同风险因子下的专家权重值,如表3所示。 步骤2根据式(15)和式(16)计算风险因子的权重w=(0.299 3,0.377 6,0.323 1)。 步骤3计算各方案的综合前景值。 首先,通过对二维二元语义进行比较,获得专家对于方案的正、负理想方案,如表4所示。 其次,参考文献[23]。令参数δ=μ=0.88,θ=2.25,κ=0.61,σ=0.69计算各专家关于故障模式的正、负前景决策矩阵(表5和表6)和风险因子权重概率函数: 表3 不同风险因子下的专家权重 表4 3位专家的正、负理想方案 表5 3位专家给出的正前景矩阵 续表5FM110.191 60.132 20.102 30.102 30.102 30.132 20.257 10.242 60.132 2FM120.279 30.203 90.132 20.203 90.243 30.354 10.279 30.243 30.203 9FM130.375 20.257 10.000 00.447 90.191 60.000 00.375 20.188 30.092 3FM140.191 60.242 60.132 20.132 20.102 30.132 20.191 60.257 10.132 2FM150.257 10.000 00.188 30.092 30.102 30.102 30.169 80.102 30.188 3FM160.169 80.092 30.203 90.000 00.132 20.203 90.000 00.000 00.188 3 表6 3位专家给出的负前景矩阵 风险因子的权重概率为:π+(w)=(0.402 7,0.454 2,0.422 3),π-(w)=(0.465 9, 0.496 9, 0.476 0)。 最后,求得各故障模式正、负前景值: V+=(0.264 3,0.242 1,0.222 8,0.211 8,0.146 9,0.267 1,0.270 8,0.258 1,0.310 5,0.135 4,0.205 6,0.287 4, 0.298 2,0.217 8,0.173 9,0.133 3); V-=(-0.531 1,-0.739 9,-0.702 2,-0.767 9,-0.771 7,-0.584 8,-0.778 6,-0.623 2,-0.652 2,-0.907 9,-0.790 9,-0.515 9,-0.505 9,-0.771 7,-0.850 7,-0.787 9) 将正、负前景值相加,得到各故障模式综合前景值: V1=-0.228 5,V2=-0.497 8,V3=-0.479 4,V4=-0.556 1,V5=-0.624 8,V6=-0.317 7,V7=-0.507 7,V8=-0.365 1,V9=-0.341 7,V10=-0.772 6,V11=-0.585 3,V12=-0.207 7,V13=-0.266 8,V14=-0.553 9,V15=-0.676 9,V16=-0.654 6。 步骤4根据综合前景值的大小进行风险排序: FM12≻FM1≻FM13≻FM6≻FM9≻FM8≻FM3≻FM2≻FM7≻FM14≻FM4≻FM11≻FM5≻FM16≻FM15≻FM10。最高失效模式为FM12(锡球/锡溅)故障模式,因此在实际生产过程中应对其优先关注,对锡球/锡溅危害进行提前重点防护。 二维二元语义中的比例系数η反应了两个维度在参与决策时的重要程度,它对距离的计算、权重的获取以及正、负理想方案都有重要的影响,因此比例系数η是十分重要的参数,为了检测比例系数η对排序结果的影响。从η=0开始η依次增加0.1,直至η=1,不同η取值排序结果如图2所示。 可以看出,当η=0至η=0.2时的排序比较稳定,说明此时第Ⅱ维信息对决策产生的影响较大,η=0.2至η=0.5时,排序较无规律,说明随着第Ⅰ维信息的比例增大,η对排序的影响开始增强,当比例系数η>0.5以后,随着η的增大,排序的变化幅度逐渐减小,其中FM12始终是最优方案,体现了该方法的稳定性。同时,从图中可以看出随着第Ⅰ维信息影响不断加强,第Ⅱ维信息影响持续降低,失效模式的排序变化始终是单向的,从侧面反映了比例系数η对排序的影响性。 为验证本文方法的可行性和有效性,将本文方法排序结果与文献[2]中的TOPSIS法、文献[12]的VIKOR法、文献[19]采用的二维二元语义法和实际故障模式的风险排序(目前对于集成电路板回流焊接风险排序方法,现场依然采用传统的FMEA法)进行对比,对比结果如表7所示。 表7 不同方法排序结果 续表7FM101616160.228166.679160.06816304FM111212140.317145.883140.08112363FM121110.77210.57610.1391601FM132340.65441.12640.1352601FM141010150.266156.203150.09010363FM151515130.365133.526100.07015245FM161414110.408124.734110.07614245 可以看出,本文方法(η=0.6)及文献[2]和文献[12]排序差异较大,这是因为文献[2]在集结专家评价信息时采用了算术平均算子,等同于各专家具有相同的重要性,但在实际评价中,每个专家的专业知识和经验是不相同的,权重应该有所差异。同时,TOPSIS法未考虑专家的主观风险态度,未能反映专家的决策心理;文献[12]中与本文方法也存在差异,主要因为文献[12]认为风险因子重要性是相同的,如FM2的排序较之前有所变化,是因为润湿不良发生频率较高,当发生频率权重变大时(相对于本文权重),导致其排序上升。文献[12]虽然认为不同的专家具有不同的重要度,但是专家权重却是事先赋予的,主观性较强。同时文献[2]和文献[12]均是一维语言变量,没有考虑专家自身评价的确认度,当η=1时,排序情况差异有所降低,这是因为当η=1时,二维二元语义降为传统的一维语言变量,不再考虑第Ⅱ维的评价信息。文献[19]的方法和本文方法η=0.5时的排序相差不大,说明本文方法的有效性,但文献[19]的专家权重依然是直接赋权的。本文方法不但能在专家和风险因子完全未知的情况下进行排序,同时还能反映两个维度重要性变化对排序的影响。 作为一种常用的风险评估方法,FMEA法虽然应用领域广泛,但由于其本身存在的不足,导致其风险排序结果较为粗糙。为了使FMEA法更好地适用于高铁信号系统的风险分析,本文在既有研究的基础上,提出一种新的改进FMEA法,相较于现有方法,具有以下优点: (1)二维二元语义的表示模型可以较好地表征风险因子的综合评估信息,它既考虑了评估信息的模糊性,又兼顾了评估信息的不确定性,为了使风险排序更加准确,提出一种新的二维二元语义的比较方法,该方法具有更好的区分度。 (2)与之前权重获取方法不同的是,本文提出一种先获取专家权重,继而确定风险因子权重的方法,使FMEA法可以适用于权重信息完全未知的群决策问题,扩大了其适用范围。同时,熵值法的运用也保证了权重的准确性。 (3)为使FMEA法更加符合真实的决策情景,将前景理论引入到FMEA法中,前景理论充分考虑了专家在决策过程中的心理特征,降低专家的主观偏好对排序结果的影响。 目前,随着企业对安全和质量重视程度的不断加深,风险管理越来越成为大家关注的重点,在未来FMEA的研究中,专家评估信息缺失、动态风险评估,以及异构评测信息融合等情况下的风险评估需要更进一步关注和探索。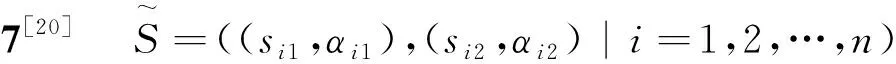
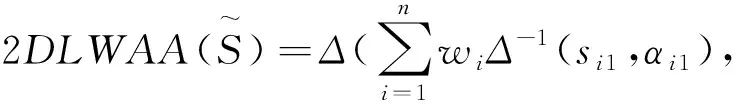
2 基于二维二元语义和前景理论的FMEA法
2.1 问题描述
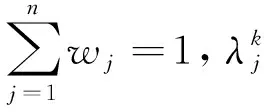
2.2 专家权重的确定


2.3 风险因子的计算

2.4 基于前景理论的风险排序
3 案例分析
3.1 集成电路板回流焊接风险分析







3.2 参数对结果的影响
3.3 对比分析

4 结束语
