一种基于SEPIC结构的非耦合电感高增益变换器

邵珠雷

(许昌学院电气与机械工程学院，河南许昌 461000)

随着新能源技术的不断发展，直流变换器被广泛应用于风电系统、光伏系统以及电动汽车系统。在光伏系统中，系统将光能转换为电能通常需要进行最大功率点跟踪且输出电压较低。这就需要光伏系统所采用的直流变换器具有连续的输入电流及较高的电压增益[1]。隔离型直流变换器通过采用变压器可以获得较高的电压增益。但是变压器增加了电路系统的体积和质量，并且其漏感会使变换器开关管两端产生尖峰电压，增大开关管的电压应力[2]。针对上述问题，非隔离型高增益直流变换器相对于隔离型直流变换器在体积、成本和功耗方面更具优势。

SEPIC 变换器具有输入电流连续的特点，适用于光伏发电等新能源系统。目前基于SEPIC 结构的非隔离型高增益直流变换器多采用耦合电感。文献[3]在SEPIC 结构中引入了耦合电感，并与二极管-电容倍压单元相结合，在提高输出电压增益的基础上，通过二极管-电容支路吸收漏感能量。文献[4]在传统SEPIC 变换器的基础上，引入耦合电感单元，并通过有源开关电感单元吸收漏感能量，减小开关管电压应力。文献[5]将BOOST 变换器与SEPIC 变换器相结合，并将电路中的电感换为耦合电感，耦合电感二次侧与倍压单元结合组成桥式倍压单元，以提高电压增益并减小开关管电压应力。在SEPIC结构中引入耦合电感能够有效地提高电压增益，但耦合电感的漏感会增加变换器开关管的电压应力。若采用钳位电路或能量吸收电路则又会增加电路的复杂度及功耗[6]。因此，本文基于SEPIC 结构提出了一种采用非耦合电感的高增益变换器。

1 电路拓扑

本文提出的基于SEPIC 结构的非耦合电感高增益变换器的电路结构如图1 所示。该变换器在SEPIC 结构的基础上加入了开关管S2、电感L2、二极管D1和电容C2。开关管S1与S2在变换器工作过程中总是同时导通和关断，电感L1和L2则以并联或串联的方式存在于变换器不同的工作模态中。电感L1、电感L2、电容C2以及二极管D1在电路中的连接结构可提高电压增益。为了便于对电路的工作过程进行分析，假设开关管与二极管为理想器件，电容足够大，电感L1与电感L2完全相等[7]。

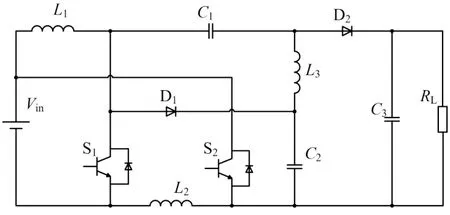
图1 基于SEPIC结构的非耦合电感高增益变换器

2 工作原理

基于SEPIC 结构的非耦合电感高增益变换器可工作于连续模式(continuous conduction mode，CCM) 和断续模式(discontinuous conduction mode，DCM)。下面将对变换器的这两种工作模式进行详细分析。

2.1 CCM

当变换器工作于CCM 时，在一个开关周期内，变换器共存在两种工作模态，其主要工作波形如图2 所示。

图2 变换器CCM的主要工作波形

工作模态1(t0≤t＜t1)：当变换器处于工作模态1 时，工作模态等效电路如图3所示。开关管S1与开关管S2同时导通，使得电感L1与电感L2以并联方式存在于电路中，电感L1两端电压及电感L2两端电压等于电源电压Vin，表达式如公式(1)所示：

图3 变换器CCM的工作模态1

二极管D1与二极管D2处于截止状态。电感L1、电感L2及电感L3充电储能，电感电流iL1、iL2及iL3线性上升。电容C1处于充电状态，电容C2处于放电状态，因此电感L3两端电压表达式如公式(2)所示：

电容C3处于放电状态，为负载提供能量，电压VC3线性下降。

工作模态2(t1≤t＜t2)：当变换器处于工作模态2 时，工作模态等效电路如图4 所示。开关管S1与开关管S2均处于截止状态，二极管D1与二极管D2均处于导通状态，使得电感L1与电感L2以串联方式存在于电路中。由于电感L1与电感L2的匝比相等，电感L1两端电压及电感L2两端电压的表达式如公式(3)所示：

图4 变换器CCM的工作模态2

电源及电感L1、L2通过二极管D2为负载提供能量，并通过二极管D1为电容C2充电，电感电流iL1、iL2线性下降，电容电压VC2线性上升。电容C1与电感L3同样通过二极管D2为负载提供能量，电感电流iL3线性下降，电容电压VC3线性上升。电感L3两端电压的表达式如公式(4)所示：

根据基尔霍夫定律及伏秒平衡原理可得，变换器工作于CCM 时的增益如公式(5)所示：

式中：Vo为输出电压；Vin为输入电压；D为占空比。

2.2 DCM

当变换器工作于DCM 时，在一个开关周期内，变换器共存在三种工作模态，其主要工作波形如图5 所示。

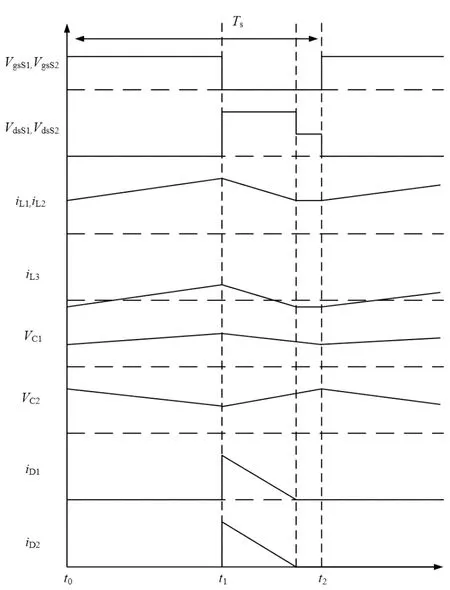
图5 变换器DCM的主要工作波形

变换器工作于DCM 的三种工作模态中，工作模态1 和工作模态2 与变换器工作于CCM 时相同。当开关管S1与开关管S2截止，流过二极管D2的电流降为零时，变换器进入DCM的工作模态3，其工作模态等效电路如图6 所示。

图6 变换器DCM的工作模态3

在DCM 的工作模态3 中，开关管S1、开关管S2、二极管D1以及二极管D2均处于截止状态。电感L1、电感L2以及电感L3两端的电压均为零。电容C1处于放电状态，电容C2处于充电状态。电容C3处于放电状态，为负载提供能量。二极管D1两端电压的绝对值与电容C1两端电压相等，二极管D2两端电压为输出电压与电容C2两端电压的差值。变换器工作于DCM的条件如公式(6)和(7)所示：

式中：RL为负载电阻值；fS为变换器工作频率；L3为电感L3的电感值。

变换器工作于DCM 时的增益如公式(8)所示：

式中：Vo为输出电压；Vin为输入电压；D为占空比。

3 变换器性能分析对比

变换器虽然能够工作于CCM 和DCM 两种模式，但工作于DCM 时变换器存在较多的弊端。比如，系统的动态响应速度较慢以及电路元件要承受更大的电流。因此，使变换器工作于CCM 是一种较为合适的应用方式[8]。下面也将针对变换器工作于CCM 时的状态进行分析与对比。

3.1 电压增益

当变换器工作于CCM 时，根据基尔霍夫定律可得：

化简可得：

根据伏秒平衡原理可得：

由公式(10)和(11)可得：

由公式(12)和(13)可得变换器工作于CCM 时的电压增益M：

由公式(15)可知，随着占空比D的不断增大，变换器的电压增益不断提升。

为了进一步了解本文所提变换器的性能的优劣，将本文所提变换器与BOOST、SEPIC、文献[9-11]进行了对比。

文献[9]所提变换器在SEPIC 结构的基础上增加了二极管DM和电容CM。电容CM连接于电感L2与地之间，有效提高了输出电压，进而提高了变换器的电压增益。二极管DM分别连接开关管S 的漏极和电容CM的正极，在提供能量通路的同时，又减小了开关管S 的电压应力。文献[9]所提变换器的电路结构如图7 所示[9]。

图7 文献[9]所提变换器的电路结构

文献[10]所提变换器为一种新型非隔离升降压直流变换器，该变换器的输入电路部分引入SEPIC 结构，以获得连续的输入电流及升降压能力。电容C2、电容C3、电容Co1、电容Co2、电容Co3、电感L3及电感L4连接构成输出电路部分，以提高电压增益，并使开关管S1的电压应力低于输出电压。文献[10]所提变换器的电路结构如图8所示[10]。

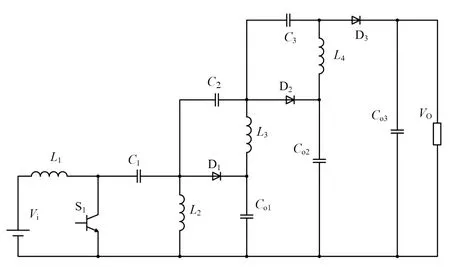
图8 文献[10]所提变换器的电路结构

文献[11]所提变换器为一种新型BUCK-BOOST 变换器，包含一个开关管、两个电感、三个电容及两个二极管。该变换器的电压增益大于传统BUCK-BOOST 变换器、CUK 变换器及SEPIC 变换器。在开关管S 关断时，二极管D1、二极管D2、电容C1及电容C2的连接结构避免了电容C1与电容C2突然转为并联，而是先分别进行充放电，有效间少了尖峰电流的出现，进而减小了电路中开关管、二极管及电容的电压应力。文献[11]所提变换器的电路结构如图9 所示[11]。

图9 文献[11]所提变换器的电路结构

本文所提变换器与BOOST、SEPIC、文献[9-11]的电压增益的对比如表1 及图10 所示。

由表1 可知，本文所提出的变换器相对于所列其他变换器具有较大的电压增益。

表1 变换器电压增益对比

由图10 可知，参与对比的变换器随着占空比的增加，其电压增益均不断提升，本文所提出的变换器在不同占空比阶段，均具有相对较高的电压增益。

图10 变换器电压增益与占空比关系对比

3.2 电压应力

当变换器工作于CCM 时，开关管S1和开关管S2的电压应力为：

二极管D1和二极管D2的电压应力为：

本文所提变换器与BOOST、SEPIC、文献[9-11]的元器件电压应力的对比如表2 及图11 所示。

表2 变换器电压应力对比

图11 开关管电压应力与占空比关系对比

由表2 可知，本文提出的变换器相对于所列其他变换器，其具有最小的开关管电压应力以及相对较小的二极管电压应力。文献[10]提出的变换器具有与本文所提变换器相近的电压增益及电压应力，但本文所提变换器所用元件总数要小于文献[10]提出的变换器。

由图11 可知，参与比较的变换器的开关管电压应力随着占空比的增大而减小，即均与占空比成反比。本文所提出的变换器在不同的占空比阶段均具有最小的开关管电压应力。

4 实验结果及分析

根据本文提出的基于SEPIC 结构的非耦合高增益变换器，试制了一台200 W 的样机，实验样机平台如图12 所示。

图12 实验样机平台

其中，输入电压Vin=20 V，输出电压Vo=250 V。变换器工作于CCM，工作频率fS=40 kHz，占空比D=74.2%。电感L1、L2、L3的电感值分别为125、125、246 mH，电容C1、C2、C3的电容值分别为4、4、15 mF。开关管S1与S2均采用IRFP260，二极管D1与D2均采用UG8GT，开关管控制芯片采用STM32F103C8。实验所得波形如图13～图20 所示。

图13 为变换器的输入电压Vin和输入电流iin的波形。由图13 可知，变换器输入电压Vin为20 V，输入电流iin连续，其平均值为1.75 A。图13 所示实验结果证明了变换器具备连续的输入电流，适用于光伏发电等新能源系统。图14 为变换器的输出电压Vo和输出电流io的波形。由图14 可知，输出电压Vo为250 V，输出电流io为0.8 A。可知，变换器输出功率达到了200 W。由图13 和图14 中的输入电压Vin和输出电压Vo可知，当占空比D为74.2% 时，电压增益为12.5，与理论分析值相近，但略微偏低。实验所得电压增益略低于理论分析值的主要原因在于，理论分析中假定了变换器所用元件均为理想元件[12]。

图13 输入电压Vin与输入电流iin

图14 输出电压Vo与输出电流io

图15 为开关管S1漏源极间电压VdsS1和流过开关管S1的电流iS1的波形。图16 为开关管S2漏源极间电压VdsS2和流过开关管S2的电流iS2的波形。由图15 和图16 可知，当工作频率fS为40 kHz，占空比D为74.2% 时，开关管S1与S2两端的电压应力相等，均为77.5 V。且由电压VdsS1和电压VdsS2的波形可知，开关管S1与S2两端在工作过程中无明显尖峰电压出现，因此电路中无需加入钳位电路。上述实验结果与理论分析一致，证明了理论分析的正确性。

图15 开关管S1漏源极间电压与电流

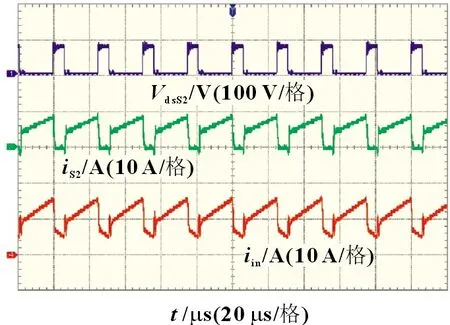
图16 开关管S2漏源极间电压与电流

图17 至图20 分别为电感L1、L2及L3两端的电压波形和流过电感的电流波形。由图17、图18 和图19 可知，当开关管S1和S2导通时，电感L1的电流iL1和电感L2的电流iL2线性上升，电感L1与电感L2两端电压相等，均为20 V。当开关管S1和S2截止时，电感L1的电流iL1和电感L2的电流iL2线性下降，电感L1与电感L2两端电压相等，均为-57 V。由图20 可知，当开关管S1和S2导通时，电感L3的电流iL3线性上升，电感L3两端电压为40 V。当开关管S1和S2截止时，电感L3的电流iL3线性下降，电感L3两端电压为-115 V。上述实验结果与理论分析一致，证明了理论分析的正确性。

图17 电感L1电流与电感L2电流

图18 电感L1电流与电压

图19 电感L2电流与电压

图20 电感L3电流与电压

5 结束语

本文提出了一种基于SEPIC 结构的非耦合电感高增益变换器，并对变换器CCM 和DCM 两种工作模式进行了理论分析。在CCM 下，将本文提出的变换器与结构相近的变换器进行了对比与分析。由对比分析结果可知，本文提出的变换器具有较高的电压增益，并具有较小的开关管电压应力和二极管电压应力。本文提出的变换器基于SEPIC 结构进行改进，在其基础上增加了四个元件，因此电路仍然具有较为简单的电路结构及较少的元器件总数。本文提出的变换器未采用变压器或耦合电感来提高电压增益，因此具有较小的体积及较小的电压应力。由于开关管的电压应力较小，使得电路中可以采用导通电阻较小的开关管，有利于降低系统的功耗[13]。由实验验证可知，本文提出的变换器在具有较高电压增益及较低电压应力的同时，又具连续的输入电流，因此非常适用于光伏发电等新能源系统。