粉土密实度对斜坡动力响应特性影响的振动台试验研究

2022-01-07李丞苏立君张崇磊蒋关鲁肖思友

中南大学学报（自然科学版） 2021年11期

李丞，苏立君,3,4，张崇磊,3，蒋关鲁，肖思友

(1. 中国科学院山地灾害与地表过程重点实验室，中国科学院·水利部成都山地灾害与环境研究所，四川成都，610041；2. 中国科学院大学，北京，100049；3. 中国科学院青藏高原地球科学卓越创新中心，北京，100101；4. 中国−巴基斯坦地球科学联合研究中心，巴基斯坦伊斯兰堡，44000；5. 西南交通大学土木工程学院，四川成都，610031)

近年来，斜坡稳定性问题引起了学者们的广泛关注。诱发斜坡失稳的因素众多，而地震荷载是其中最重要的因素之一。据调查，2008 年汶川地震和2013 年芦山地震时，土质地震滑坡在地震滑坡灾害中占比较大[1−3]。因此，开展地震作用下土质斜坡的动力响应特性的研究，对土质斜坡的抗震设计具有重要意义。

振动台试验是深入研究地震作用下土质斜坡动力响应特性的重要方法。人们利用振动台试验分析了影响土质斜坡动力响应特性的因素，如坡体形状[4]、地震波形[5]、地震波频率[6]、土体材料[7]、土体含水率[8]等。上述研究对工程师理解土质斜坡的动力响应特性起到了关键的作用[4−8]。然而，由于土质斜坡动力响应特性复杂，许多规律尚需进一步研究，如土体密实条件对斜坡动力响应特性的影响。土体密实度是评价土体物理力学性质的重要指标之一，大量室内土工试验表明土体密实条件改变了土体剪切模量和土颗粒间接触力，进而影响土体动力特征[9−11]。然而，土体密实度如何影响斜坡动力响应特性仍不明确，目前关于此方面的研究报道较少。

人们通过改变土体的压实度研究了粗粒土边坡的地震响应，但现有研究存在以下问题[12−14]：1)研究主要针对粗粒土压实度对边坡动力响应特性的影响，而对细粒土边坡的研究较少。2)使用较少的指标来研究斜坡的动力响应特性。林宇亮等[12−13]研究了4 个不同压实度边坡的加速度响应和频谱特性，分析了4个不同压实度边坡的地震残余变形特性。刘威[14]分析了2个不同压实度边坡的加速度响应规律和位移变化规律。3)林宇亮等[12]在4个不同压实度边坡表面安装了4 个加速度传感器，没有讨论斜坡内部加速度响应随坡高的变化规律。4)现有研究和规范缺乏直接定量判别土体压实度大小的分级指标，使工程师只能依靠经验判断土体压实度，给快速评价边坡的地震响应带来了一定的困扰。密实度可综合反映土颗粒的矿物组成、颗粒级配、颗粒形状等对工程性质的影响，可以直观地判断土体的工程性质，无论是粗粒土还是细粒土(仅含粉土)都有具体的分级指标[15]。因此，针对上述问题，深入研究粉土密实度对斜坡在地震荷载作用下动力响应的影响对土质边坡动力响应特性的研究具有一定价值。

为区分不同密实度粉土斜坡的动力响应特性差异，本文作者设计并完成2组不同密实度斜坡的大型振动台模型试验。试验采用不同峰值加速度的正弦波和人工波作为地震激励，研究不同密实度对粉土斜坡的自振频率和加速度响应的影响，揭示斜坡的频谱特性和动位移的变化规律，探讨不同地震强度作用下土体剪应力−剪应变曲线的响应形式和发展水平，以期为土质斜坡的抗震设计提供参考。

1 试验方案设计

1.1 试验设备

试验在西南交通大学单向电液伺服驱动式地震模拟振动台进行，振动台台面长×宽为4 m×2 m，最大荷载为25 t，最大加速度为1.2g，最大速度为0.4 m/s，频率范围为0.40～15.00 Hz，水平位移范围为[−100，100] mm。试验采用刚性模型箱，内部长×宽×高为3.7 m×1.5 m×2.1 m。为了减少地震波沿边界的反射，尽量减小模型箱效应，在箱的内壁衬以厚度为8 cm 的橡胶垫和聚乙烯泡沫塑料等柔性材料。此外，在平行于振动方向的两侧壁面涂抹凡士林，以减小模型土体与模型边壁的摩擦。

1.2 相似关系设计

在大多数振动台模型试验中，物理量的模型相似比主要受斜坡几何比的控制，故模型试验结果可以在一定情况下模拟多个原型边坡[5]。本文所模拟的斜坡是一种概化的斜坡模型，不针对具体斜坡。结合振动台尺寸和以往的研究[4−8,12−14]，本文的原型与模型的相似比为1∶15。为了使模型试验尽可能地反映原型的动力响应特性，通常需要考虑影响试验对象的主要因素，忽略次要因素，因此，在试验中保持原型与模型的土体密度相同，选取密度(重度)作为模型试验的主控因子可简化制样过程[15−16]，试验在重力场下进行。将几何比l、重度γ、输入加速度a、重力加速度g、黏聚力c、内摩擦角φ、应变ε、应力σ、时间t和频率f作为主要相似指标，由物理条件、几何条件和动态平衡条件间的相似关系得到以下相似准则：

式中：λl为几何比的相似因子；λγ为重度的相似因子；λa为输入加速度的相似因子；λg为重力加速度的相似因子；λc为黏聚力的相似因子；λφ为内摩擦角的相似因子；λu为位移的相似因子；λε为应变的相似因子；λσ为应力的相似因子；λt为时间的相似因子；λf为频率的相似因子。

以几何比l、重度γ、输入加速度a为主控因素，按照Bockingham π 定理推导物理量相似常数[17]，结果见表1。

表1 模型物理量相似常数Table 1 Similarity ratio of model’s physical parameters

1.3 试验工况设计

试验材料为粉土，颗粒级配曲线如图1 所示。试验材料的基本参数如表2 所示。在GB 50021—2001“岩土工程勘察规范”中，粉土根据孔隙比进行密实度分类[17]：1) 当孔隙比e<0.75 时，粉土为密实粉体；2) 当0.75≤e≤0.90 时，粉土为中密粉体；3)当e>0.90 时，粉土为稍密粉体。根据粉土密实条件的分类，共设计2组试验。1号斜坡的天然密度为1.65 g/cm3，孔隙比为0.88(中密)，2 号斜坡的天然密度为1.35 g/cm3，孔隙比为1.30(稍密)。2组试验材料的物理力学指标如表3 所示。2 组斜坡采用控制体积法分层填筑，每次填高5 cm。在填筑过程中，用恒定力对土体进行碾压以确保土体孔隙率尽可能均匀分布。模型填筑完成后，静置24 h。

表2 试验材料的基本参数Table 2 Basic parameters of test materials

表3 2组斜坡材料的物理力学指标Table 3 Physico-mechanical indexes of two cases

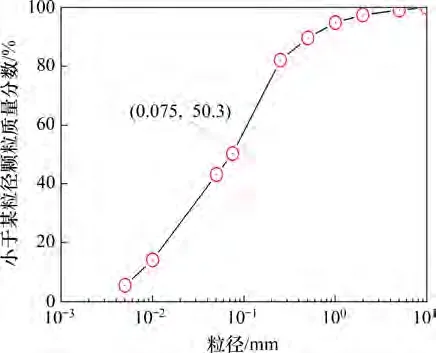
图1 颗粒级配曲线Fig.1 Distribution curves of particle-size

2 组试验斜坡概化模型的设计坡度为37°，模型坡高为140 cm，几何比l为15，即原型坡高为21.0 m，斜坡模型设计如图2所示。试验共布置15个加速度计和2 个水平位移计。加速度计A0 用于监测台面的水平向加速度。加速度计A1～A7 和A8～A14 分别监测斜坡内部和表面的水平向加速度。位移计D1 和D2 用于监测斜坡上部表面的变形。

图2 斜坡模型和传感器布置Fig.2 Slope model and sensors layout

1.4 地震波加载序列

2组试验采用单向水平输入，输入波为人工波和正弦波，真实地震记录的主频通常为0.10～10.00 Hz。输入正弦波的频率为5.00 Hz，持续时间为8.2 s，输入人工波第一阶自振频率为3.25 Hz，持续时间为52 s，典型的人工波信号如图3 所示。由图3 可见：输入地震波振幅从0.10g递增至0.30g，间隔0.10g。在加载波幅值或波形发生变化时输入幅值为0.05g、历时30 s 的白噪声，白噪声的频率范围为0.50～50.00 Hz。利用白噪声对斜坡进行扫频，测定斜坡的动力特性，具体的加载序列见图4，其中，aPGA为峰值地面加速度。

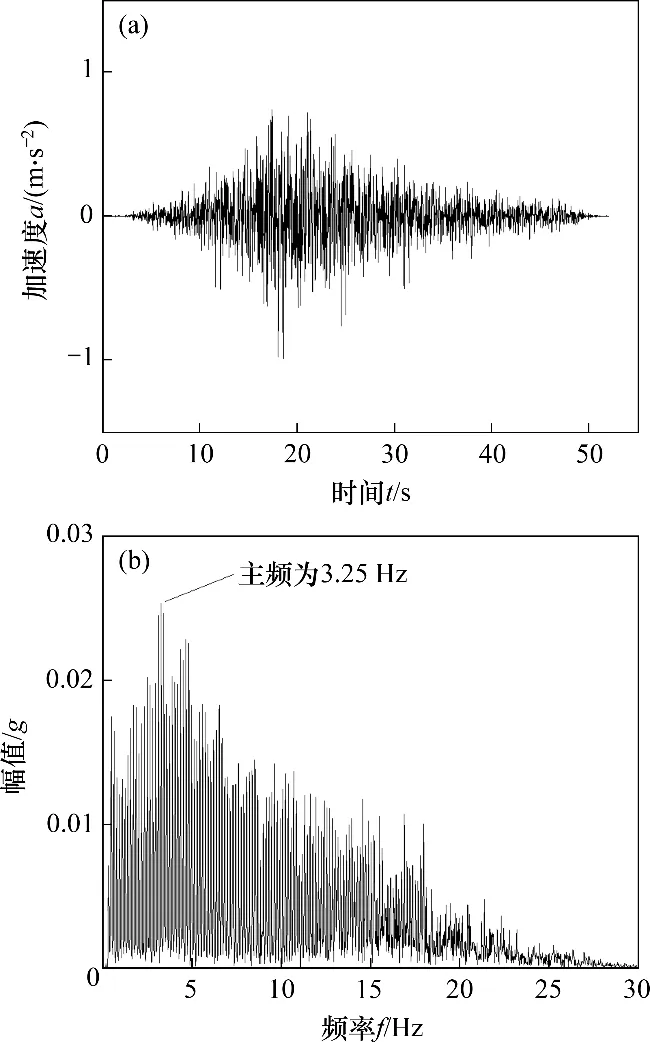
图3 输入典型人工波信号Fig.3 Typical artificial wave signals for input

图4 试验的加载序列Fig.4 Loading sequence employed during tests

基于2个斜坡在白噪声激励下的响应信号，利用Tfestimate 函数得到斜坡的传递函数虚部。图5所示为1 号和2 号斜坡在白噪声工况2 时不同监测点处的传递函数虚部计算结果，1 号和2 号斜坡的自振频率分别为31.25 Hz和24.41 Hz，自振频率为5 个测点(A1～A5 所在位置，下同)得到的主频的均值[18−19]。2 组试验的自振频率变化率随加载历程的变化如图6所示。得到第一个加载工况产生的自振频率与每一个加载工况产生的自振频率的差值，用此差值除以第一个加载序列产生的自振频率的比值即为自振频率变化率。由图6可知：随不同地震动序列的加载，自振频率变化率呈现上升趋势，但上升幅度有所不同。对比试验前后的自振频率变化率可知，1 号和2 号斜坡自振频率变化率升幅分别为4.36%和9.18%，这表明1 号斜坡的剪切模量比2号斜坡的剪切模量大，且2号斜坡的内部结构在持续地震荷载作用下比1号斜坡的恶化程度更大。以图6中A点和B点为例，1号和2号斜坡的自振频率变化率呈下降趋势，这是由于斜坡在较小地震作用下，振动使斜坡密实度增大[17−19]。

图5 白噪声工况2下2个斜坡的传递函数虚频特性曲线Fig.5 Characteristic curves of imaginary part of transfer function at different measuring points at white noise condition 2

图6 自振频率变化率随加载历程的变化曲线Fig.6 Curves of natural frequencies change rate with loading process

2 试验结果分析

2.1 加速度放大系数分析

定义斜坡加速度放大系数为各测点的加速度峰值与台面测点峰值之比的绝对值。不同地震波作用下2组斜坡各测点的加速度放大系数如图7所示。由图7可知：波形对1号斜坡的加速度放大系数无实质性影响。对2号斜坡而言，当峰值地面加速度aPGA≤0.20g时，正弦波加载的加速度放大系数比人工波的加速度放大系数略大；当aPGA=0.30g时，正弦波加载的加速度放大系数比人工波的系数大。

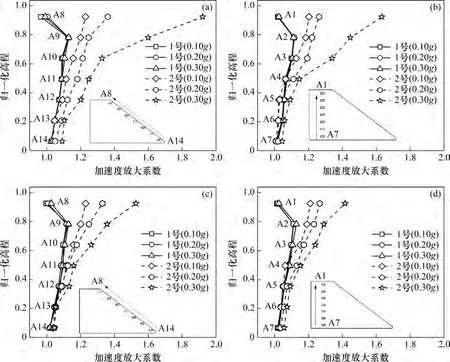
图7 加速度放大系数随高程和aPGA的变化关系Fig.7 Changes of acceleration amplification factor with elevation and aPGA

此外，坡体高程增加，1号斜坡加速度放大系数呈先增大后减小趋势，加速度放大系数数值均较小，为1.021～1.150，且最大值不在坡顶，而在0.78H坡高处。这是由于1 号斜坡整体性较好，在试验过程中尚处于线弹性阶段，传递到坡顶的地震能量较少[5]。对2 号斜坡而言，当aPGA≤0.20g时，随坡体高程增加，2号斜坡加速度放大系数呈缓慢增长趋势，这表明斜坡动力响应未被完全激发；而当aPGA=0.30g时，对正弦波而言，坡面和坡内的加速度放大系数随坡高的增大分别增加了43.1%和36.0%，对人工波而言，坡面和坡内的加速度放大系数随坡高的增大分别增加了31.3%和25.3%。这是由于2号斜坡结构松散，坡肩为坡面和坡顶的交汇点，该点会出现较多地震波反射(叠加)现象，其加速度响应剧烈，这表明稍密状态斜坡的上部应该受到更多重视。另一方面，1号斜坡的坡面加速度放大系数和坡内加速度放大系数的差异微小，为0.001～0.025。当aPGA=0.30g时，正弦波加载下的2号斜坡坡面加速度放大系数和坡内加速度放大系数的差异随坡高增加显著增大，表现为趋表放大效应，即越接近坡面与坡顶，放大效应越明显。

为加深土质斜坡动力响应的理解，对本文斜坡的加速度放大系数和国内外学者所得加速度放大系数进行比较[5,6,20−21]，如图8 所示，各组试验参数见表4。由图8 与表4 可知：当输入地震强度较小(点1)或斜坡刚度较大(点2)时，斜坡加速度放大系数随坡高先增大后减小，且加速度放大系数数值偏低，这与1号斜坡的加速度响应规律一致；增大地震强度或减小斜坡刚度，加速度响应规律发生改变，具体表现为加速度放大系数随坡高增大而增大[20−21]。据此可以推断，由于1 号斜坡具有较高的刚度，输入1号斜坡的地震能量((0.10～0.30)g)尚不足以改变其加速度响应规律，这与文献[5]中砂土边坡显示的规律一致，若持续增大地震能量((0.20～0.40)g)，1 号斜坡的加速度响应规律可能会发生改变。2号斜坡加速度放大系数与坡高的关系与文献所得研究结果一致[5,6,20−21]，表现为加速度放大系数随坡高增大而增大。以上分析表明：尽管斜坡形状、材料和地震激励可能存在差异，但不同斜坡的加速度响应呈现出相似的变化，即1号斜坡的加速度响应最大值受斜坡中、上部控制，而不是由斜坡顶部控制[5,20−21]，2号斜坡的加速度响应随坡高增大而增大，这种现象在模型试验和现场观测中更为常见[6,21−23]。

表4 图8中的试验参数Table 4 Experimental parameters in Fig.8

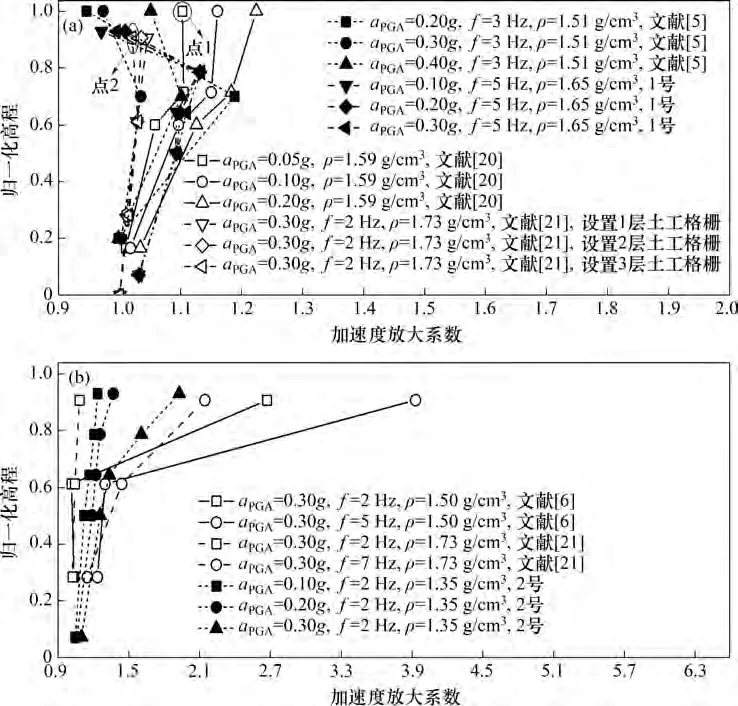
图8 以往研究结果与本研究结果的比较Fig.8 Results of previous studies compared with those of this study

2.2 加速度傅里叶谱分析

土体密实度对斜坡的加速度响应有显著影响。对2 组斜坡坡面测点的傅里叶谱变化规律进行探讨，结果如图9所示。从图9可知：傅里叶谱能量幅值随输入aPGA增大而增大。1 号斜坡傅里叶能量幅值随高程先增大后减小，在高程110 cm 处，能量幅值达到最大值。2号斜坡傅里叶能量幅值则随高程单调增加，在坡顶达到最大值。傅里叶谱能量幅值的分析结果与加速度放大系数分布结果一致。

图9 坡面测点的FFT能量幅值随加载aPGA和高程变化Fig.9 FFT spectrum of energy amplitudes change with aPGA and elevation at points of slope surface

图10 所示为不同能量幅值加载条件下2 个斜坡坡面测点(A8和A13所在位置)和坡内测点(A1和A6所在位置)的傅里叶谱曲线。由图10可知：地震能量和测点位置对1号斜坡的主频影响较小，保持在3.93 Hz 附近，与人工波FFT 谱的主频(3.25 Hz)差值仅为0.68 Hz；当aPGA分别为0.10g和0.30g时，2号斜坡下部测点的主频分别为3.93 Hz和4.06 Hz，与输入人工波FFT 谱的主频(3.25 Hz)差值分别为0.68 Hz和0.81 Hz。然而，坡体顶部的测点的主频分布在15.50～15.54 Hz 和16.98～16.98 Hz 附近的高频段，与人工波FFT谱的主频(3.25 Hz)差值分别达12.25～12.29 Hz 和13.67～13.73 Hz。这表明随高程增加，坡体会对中高频段产生选择性放大作用。以上分析表明，在地震波经坡体由下至上传播的过程中，1 号斜坡的内部结构保持了较好的完整性，频谱曲线没有发生实质性改变；而2号斜坡的内部结构变得更加松散，坡体顶部频谱曲线形状发生了显著变化。

图10 FFT能量幅值随PGA和测点位置的变化Fig.10 FFT spectrum of energy amplitudes change with PGA and position

2.3 动位移分析

阶段位移定义为单次地震波作用下位移计记录的位移增量，永久位移定义为多次地震波作用下阶段位移的和。2 个斜坡的D1 位移计所在位置(坡体上部，见图2)和D2 位移计所在位置(坡体中部)在0.10～0.30g正弦波作用下的位移−时程曲线如图11所示。从图11可知：1号斜坡的D1所在位置和D2 所在位置的永久位移分别为1.55 mm 和0.10 mm，而2 号斜坡的D1 所在位置和D2 所在位置的永久位移分别为3.27 mm 和1.13 mm。通过表1所示的相似关系将模型永久位移转换成原型的位移，得到正弦波加载下1号原型斜坡和2号原型斜坡D1 所在位置的永久位移分别为2.30 cm 和5.60 cm。使用相同方法得到人工波加载下2 个原型斜坡的永久位移。图12 所示为在0.10～0.30g正弦波和人工波作用下2 个原型斜坡D1 所在位置和D2 所在位置的永久位移。由图12 可知：1 号原型斜坡和2 号原型斜坡D1 所在位置的永久位移分别为6.39 cm和2.43 cm。

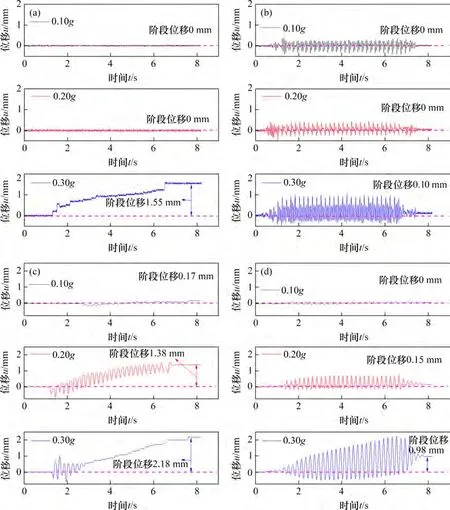
图11 正弦波加载下的斜坡位移−时程曲线Fig.11 Displacement−time history curves of slopes under sine wave loadings

图12 原型斜坡永久位移Fig.12 Permanent displacement of prototypeslopes

目前，国内规范对边坡永久位移的临界值没有明确界定，因此，参考JIBSON[24]关于边坡永久位移量的分级标准，即：当永久位移为[0，1)cm时，边坡处于低危险程度；当永久位移为处于[1，5)cm 时，边坡处于中危险程度；当永久位移为[5，15)cm时，边坡处于高危险程度；当永久位移大于15 cm时，边坡处于超高危险程度。根据此分级方法，当加载aPGA为0.30g的地震能量后，1号斜坡和2 号斜坡分别处于中危险程度和高危险程度。这也从侧面验证了2号斜坡表面的加速度放大效应比1号斜坡的放大效应大。

2.4 土体剪应力−剪应变分析

人们使用垂直阵列提供的实测加速度获得水平地面和斜坡的剪应力−剪应变曲线[25−26]。此方法考虑水平剪切波在土体中的垂直传播，假定土沿重力方向的动态变形符合一维剪切梁模型，且表面是剪应力−剪应变为零的自由表面。剪应力、剪应变和剪切模量的计算步骤参照文献[25−26]中的方法进行。图13 所示为A2 所在位置(斜坡上部)和A6 所在位置(斜坡下部)在aPGA分别为0.10g和0.30g，在正弦波作用下，2 组斜坡土体的剪应力−剪应变滞回曲线。由图13可知：1号斜坡的剪应力−剪应变滞回曲线呈单调线性往复循环发展，这说明土体仍处于线性发展阶段；当aPGA为0.10g时，2号斜坡的剪应力−剪应变滞回曲线表现出良好的对称性，这说明土体仍处于线性发展阶段；当aPGA为0.30g时，剪应力−剪应变滞回区面积逐渐增大，对角线斜率逐渐减小，剪切模量逐渐减小，这表明土体已进入非线性发展阶段。

图13 正弦波作用下斜坡的剪应力−剪应变变化曲线Fig.13 Shear stress−strain histories of slopes under loading sine waves

为了揭示剪切模量与剪应变之间的关系，利用图13 所示的剪应力−剪应变滞回曲线计算A2 所在位置和A6 所在位置的2 组斜坡剪切模量，结果如图14 所示。由图14 可知：2 组斜坡的剪切模量随aPGA和斜坡高度的增加而减小，且斜坡上部的剪应变比下部的剪应变大，斜坡上部的剪切模量比下部的剪切模量小。对于1号斜坡而言，当单次正弦波加载时，剪应变变化较小，以A2 所在位置aPGA为0.10g时为例，剪应变在0.150%～0.158%范围内变化。此外，当aPGA从0.10g加载到0.30g时，A2和A6处的剪应变分别增加了0.367%和0.254%。对于2 号斜坡而言，当aPGA为0.10g时，剪应变变化较小。当aPGA为0.30g时，A2 和A6 处剪应变迅速增大，A2 和A6 处的最大剪应变分别达1.650%和1.220%，与加载aPGA为0.10g时的剪应变相比，A2和A6处的剪应变分别增加了1.522%和1.078%。这说明2号斜坡已进入大应变发展阶段(大于1%的应变称为大应变[27])，土体的塑性变形不断产生和累积。此外，加载0.30g正弦波后，A2 处1 号和2号斜坡的剪切模量范围分别为86.83～91.00 kPa 和64～69.16 kPa，表明1 号斜坡的剪切模量比2 号斜坡的大，这与自振频率变化率的分析结果一致。