剪力键抗剪刚度对组合梁桥收缩徐变的影响分析

鹿俊杰， 赵 青

(安徽建筑大学 土木工程学院， 安徽 合肥 230601)

钢混组合梁桥在国外发展已久，随着经济水平和桥梁工程领域的发展在国内也得到了越来越多的应用。钢混组合梁桥是由两种性质差别较大的钢材和混凝土通过抗剪连接件组成的一个整体，能发挥组合结构的优势，拥有众多优点。同时，混凝土材料的存在，会导致结构受收缩徐变的影响[1]。收缩和徐变是影响混凝土力学性能和变形的两个重要影响因素[2-4]。混凝土收缩徐变产生变形，也会导致钢梁产生内力重分布和附加变形，研究钢混组合梁桥结构混凝土收缩徐变是一个很重要的问题。钢混组合梁桥剪力键抗剪刚度是影响梁桥收缩徐变的重要因素之一[5-7]。通过有限元软件Midas/Civil建立相应模型，探索剪力键抗剪刚度对挠度和应力的影响规律，为桥梁工程的设计与施工提供有益参考。

1 有限元模型

1.1 模型假设

(1)钢混组合梁桥不考虑相对滑移；

(2)模型不考虑组合梁桥坡度的影响以及温度应变的影响。

1.2 工程实例

某钢混组合梁桥的上部结构为三跨连续组合梁桥(35 m + 45 m + 35m)，总长度115 m，从上往下依次为0.3 m厚混凝土桥面板、4.5 m高钢梁和4.8 m高钢混组合梁桥断面。混凝土桥面板采用C50混凝土，上下分别铺设36根直径为25 mm的纵向钢筋。槽型钢梁材料采用Q345。桥梁跨度方向上均布φ20剪力钉。

1.3 有限元模型

用有限元软件Midas/Civil建立模型，该模型一共有个123节点，122个单元。有限元模型如图1所示。

图1 有限元模型

1.4 施工步骤

将模型分为7个施工阶段：第一阶段为钢梁架设，持续时间为3 d；第二阶段为钢梁拼接，持续时间为2 d；第三阶段为正弯矩部位混凝土的浇筑，浇筑时长为7 d；第四阶段为负弯矩部位混凝土浇筑，浇筑时长为7 d；第五阶段为去除临时支座，用时为2 d；第六阶段为混凝土桥面板上的防护层铺装，用时为15 d；第七阶段为混凝土收缩徐变，考虑研究目的假设用时为10 a。

1.5 收缩徐变本构模型

以粘弹性本构理论[8]为基础，水泥体是弹性水泥凝胶骨架。为了简化计算，忽略温度应变的影响，混凝土在应力、收缩下的应变公式为：

ε(t)=J(t,t0)σ+εcs(t)

(1)

(2)

其中：J(t,t0)是柔度函数,εcs(t)是收缩应变，φ(t,t0)是徐变系数。由式(1)和式(2)可知混凝土的应变为：

(3)

1.6 混凝土收缩模型

收缩是混凝土自身的特点，由材料内部水分变化引起。考虑混凝土的材料特性，混凝土的收缩应变为：

εcs(t,ts)=εcs0βs(t-ts)

(4)

εcs0=[1.6×10-4+10-5βsc(9-fcm/fcm0)]βRH

(5)

(6)

βRH=-1.55[1-(RH/RH0)3]

(7)

式(4)中，βs(t-ts)是收缩发展系数。式(5)中，βRH为环境年平均湿度系数。由式(4)～式(7)可知收缩应变为：

(8)

1.7 混凝土徐变模型

建立混凝土徐变模型的目的是为了准确衡量混凝土徐变，在所有的影响因素中徐变系数最为关键。混凝土徐变系数为：

φ(t,t0)=φ0βc(t-t0)

(9)

(10)

(11)

(12)

式(9)中，φ0是名义徐变系数，βc(t-to)为徐变随t变化系数。由式(9)～式(12)可知混凝土徐变系数为：

(13)

2 有限元模型的结果分析

2.1 剪力键抗剪刚度对挠度的影响

剪力键是钢梁和混凝土桥面板联系的关键，是构成整体结构的重要组成环节。剪力键在整体结构当中承担剪力，阻碍由剪力引起的变形，同时还能起到抗倾覆和相对滑移的作用。栓钉在剪力键中的应用最为常见，工程实例中采用均布φ20剪力钉。工程中剪力键刚度有限，取值不是无限大。有限元模型假设时不考虑钢混组合梁桥相对滑移，但是在实际情况中，钢梁和混凝土桥面板联系截面处会产生相对滑移，相对滑移量的大小受到剪力键抗剪刚度的影响。

为分析剪力键抗剪刚度对梁桥挠度的影响情况，取第一跨跨中、第二跨跨中截面为关键截面。剪力键抗剪刚度K分别取值为50 kN·mm-1、100 kN·mm-1、500 kN·mm-1。为了更好地研究混凝土收缩徐变，统计10 a的变化情况。第一跨跨中挠度变化和第二跨跨中挠度变化如图2和图3所示。

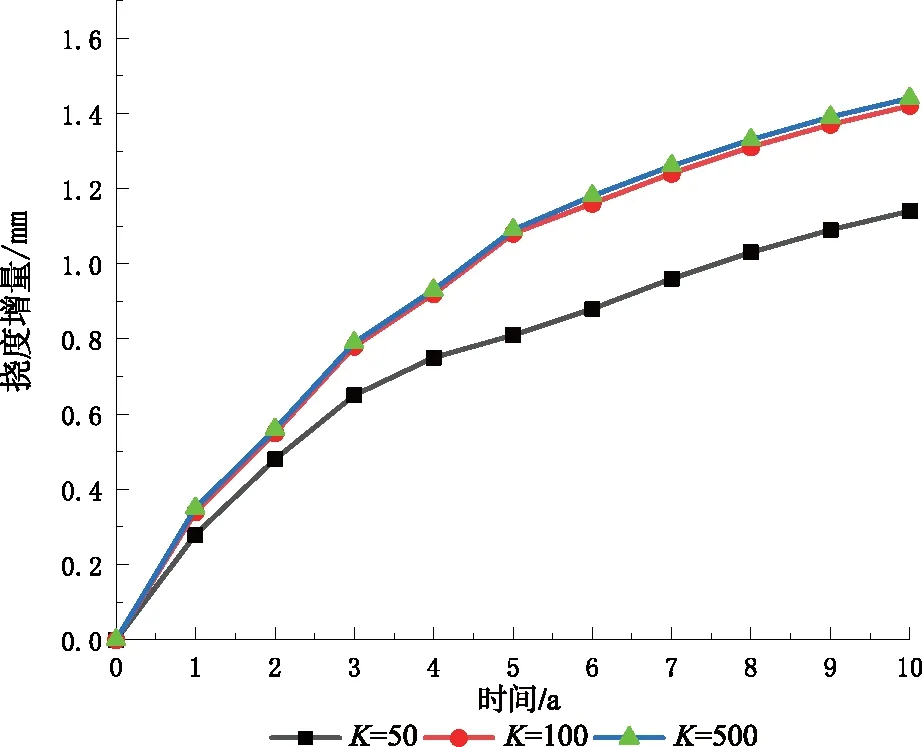
图2 第一跨跨中挠度变化图

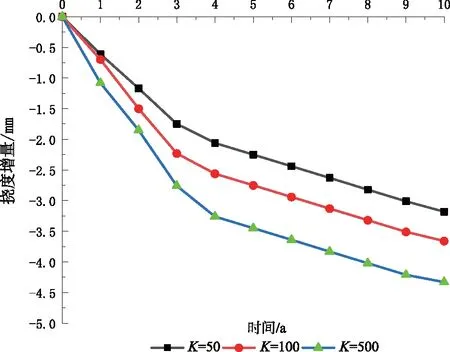
图3 第二跨跨中挠度变化图

由图2和图3可知，剪力键抗剪刚度对桥梁挠度影响较大，挠度随时间呈非线性变化，初期变化较快，后期变化较慢。第二跨跨中截面比第一跨跨中截面挠度大，更容易发生破坏。随着剪力键抗剪刚度K增大，第一跨跨中、第二跨跨中截面挠度皆有明显增加。

2.2 剪力键抗剪刚度对应力的影响

为分析剪力键抗剪刚度对梁桥应力的影响情况，使混凝土收缩徐变得到充分发展，以钢混组合梁桥建成10 a为时间节点进行分析，对比成桥时的应力情况。取第一跨跨中、第二跨跨中截面为关键截面，截面位置处的应力值如表1～表4所示。

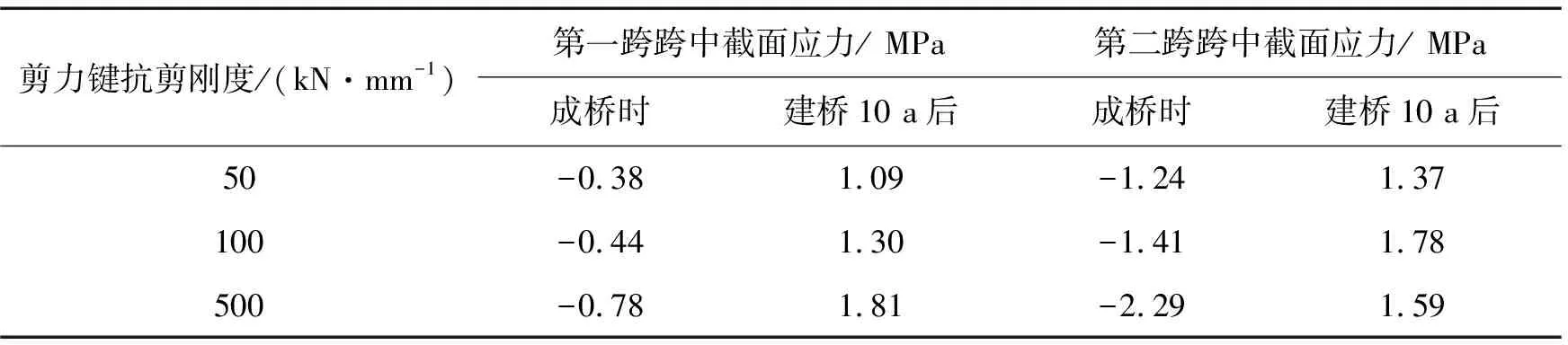
表1 混凝土桥面板上边缘应力表

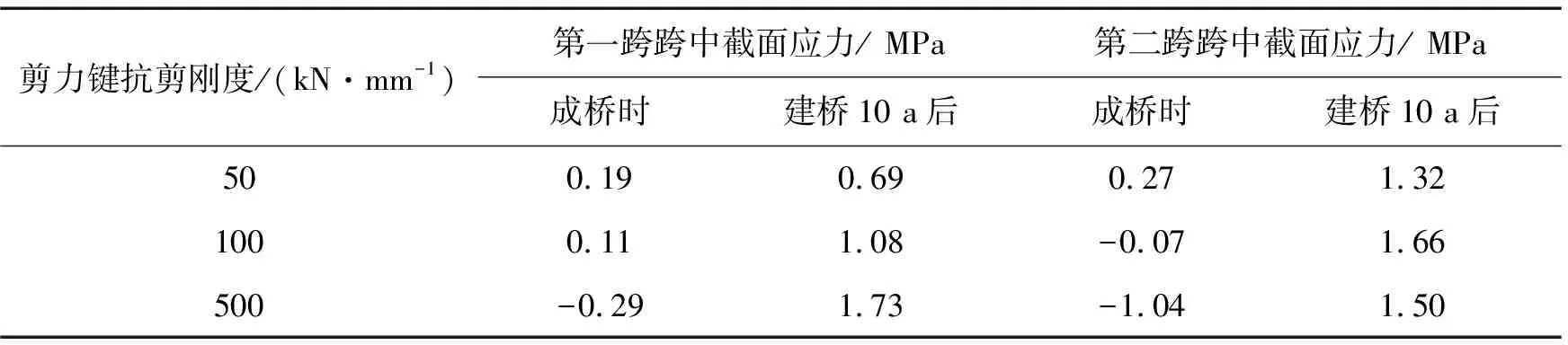
表2 混凝土桥面板下边缘应力表

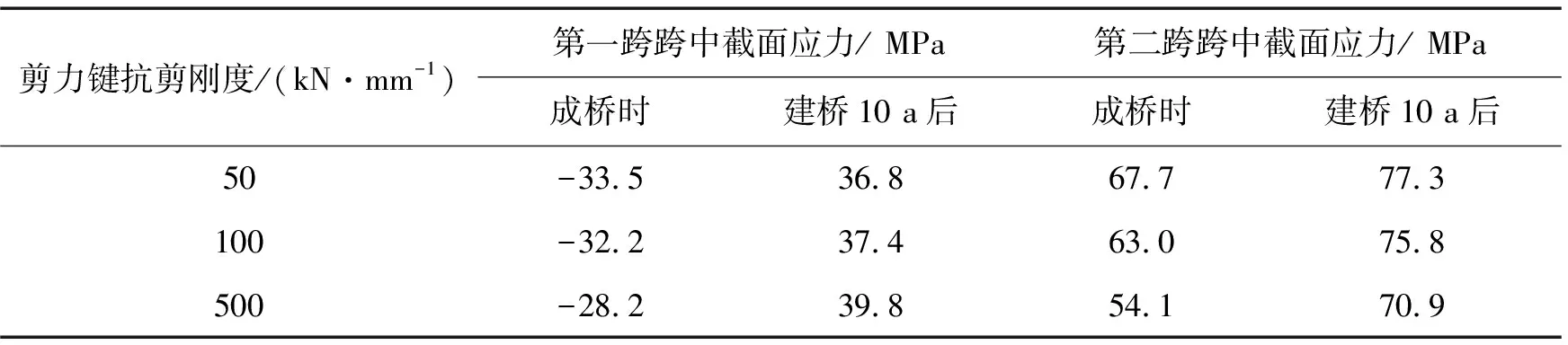
表3 钢梁上边缘应力表

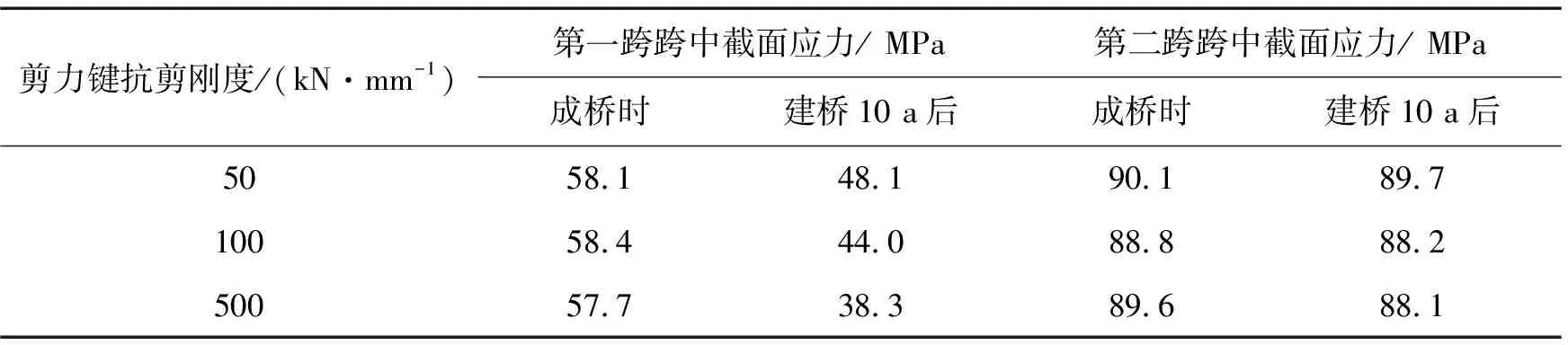
表4 钢梁下边缘应力表

由表1～表4可得，剪力键抗剪刚度对桥梁应力影响较大，在建桥10 a混凝土收缩徐变充分发展后，应力变化更加明显。而且第二跨跨中截面应力值比第一跨跨中应力大，更容易发生破坏。

由表1～表2可得，对混凝土桥面板而言，混凝土桥面板上边缘比下边缘应力大，刚好符合混凝土桥面板受压的特点。建桥10 a后混凝土收缩徐变得到充分发展，第二跨跨中截面混凝土桥面板应力随剪力键刚度的增加先增大后减小。

由表3～表4可得，对钢梁而言，钢梁下边缘应力比上边缘大，刚好符合钢梁受弯的特点。建桥10 a后混凝土收缩徐变得到充分发展，第二跨跨中截面钢梁应力随剪力键刚度的增加而减小。

3 结 语

(1)钢混组合梁桥挠度随时间非线性增加，初期变化较快，后期变化较慢。在一定范围内，随着剪力键抗剪刚度增大，第一跨跨中、第二跨跨中截面挠度皆有明显增加。

(2)钢混组合梁桥应力分两个部分进行分析，对混凝土桥面板而言，混凝土桥面板上边缘应力比下边缘大。建桥10 a后混凝土收缩徐变得到充分发展，在一定范围内，第二跨跨中截面混凝土桥面板应力随剪力键刚度的增加先增大后减小；对钢梁而言，钢梁下边缘应力比上边缘大，建桥10 a后混凝土收缩徐变得到充分发展，在一定范围内，第二跨跨中截面混凝土桥面板应力随剪力键刚度的增加先增大后减小。

(3)剪力键抗剪刚度对钢混组合梁桥收缩徐变的影响很大，体现在对梁桥挠度和应力的影响上，尤其在梁桥跨中截面处，在设计和施工过程中应得到充分重视。