变电站巡检机器人路径规划智能算法优化

韩耀廷，赵志梅，郝晓宇，刘亦鑫

（内蒙古电力集团蒙电信息通信产业有限责任公司，呼和浩特 010020）

0 引言

变电站巡检是保证变电站稳定运行的重要工作之一，传统巡检工作由人工完成，对工作人员的要求较高，而且变电站存在异常情况时，易造成人员伤亡和经济损失，给电网的安全稳定运行带来不良影响。随着人工智能产品的成熟，部分变电站的巡检工作已逐步由巡检机器人代替[1-2]。巡检机器人可通过各种传感器对变电站中设备的各项指标进行检测，同时，后台管理系统可对采集的数据进行自动分析、实时预警[3-4]。巡检机器人在巡检工作中依赖的导航技术包括全局路径规划、机器人地图定位、指示机器人局部行为等（其中全局路径规划是最核心技术）。目前采用A*算法进行巡检路径规划时，在启发式前期将某些潜在的最优节点无差别删除，导致在某些情况下无法找到全局最优路径，只能寻得次优路径，使得巡检效率较低[5-6]。本文从增加搜索邻域节点和提升算法效率两个角度优化传统A*算法，以提升路径规划的效果和效率。

1 A*算法路径规划存在的问题

针对机器人外界环境及人为因素，采用智能算法规划巡检路径，定义一条最优路径或次优路径，以检测变电站内部关键位置，采集重要设备信息，这个过程要求巡检机器人无碰撞到达[7-8]。在基于栅格法建立的变电站地图中，路径规划通常采用基于启发式的搜索算法和基于智能路径的规划算法[9-10]。

启发式算法中常用的是A*算法，该方法在静态环境中有较好的路径规划能力[11-12]。然而在以栅格为基础的A*算法中，每个栅格的中心都存储着节点的所有状态信息（见图1），节点临近的8个区域都是这个节点的扩展方向，即该节点在选择下一个行进点时，周围最多存在8个（有可能存在障碍点）待选行进点，因此运动方向的角度被限定为π/4的整数倍[13-14]。由于受到行进方向的限制，使用A*算法在栅格地图上进行巡检机器人路径规划时，规划出的路径不平滑，增加了路径长度，可能不是最优路径，巡检效率不能达到最优[15]。图2为采用以栅格为基础的A*路径算法规划X点到Y点的巡检路径（无障碍点）。从规划效果看，规划路径并不是最优路径，存在转折点复杂、转折次数多、平滑性欠缺等问题。

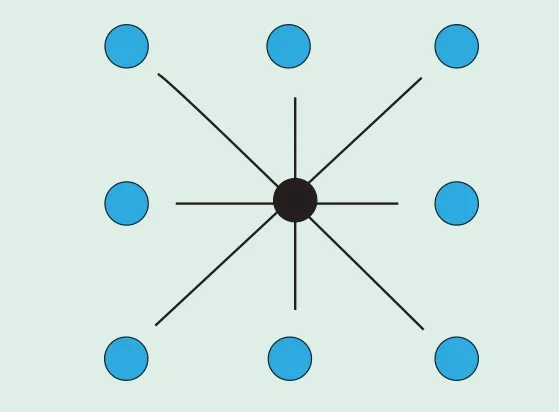
图1 A*算法8邻域示意图

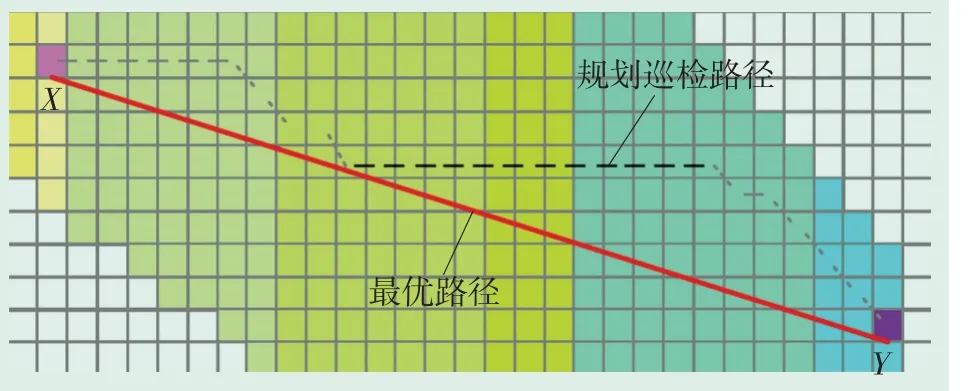
图2 A*算法规划路径

2 算法改进

为了使路径规划更加合理，对传统A*算法进行改进。将传统A*算法每个节点的扩展个数从8个邻域增加至16个邻域，扩展后的邻域示意图见图3。同时，采用最小二叉堆对传统A*算法的OPEN列表按照欧氏距离由小到大的顺序在堆中有序存储，每次取堆中第一个元素即为路径中代价最小的节点，16邻域A*算法路径规划流程见图4。具体流程如下。

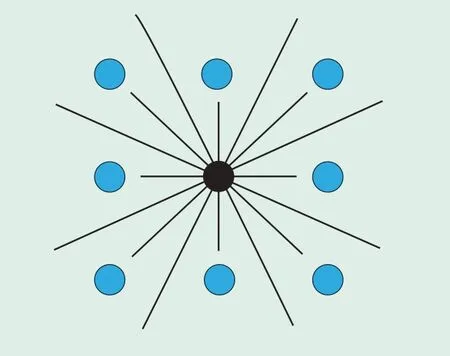
图3 A*算法16邻域示意图

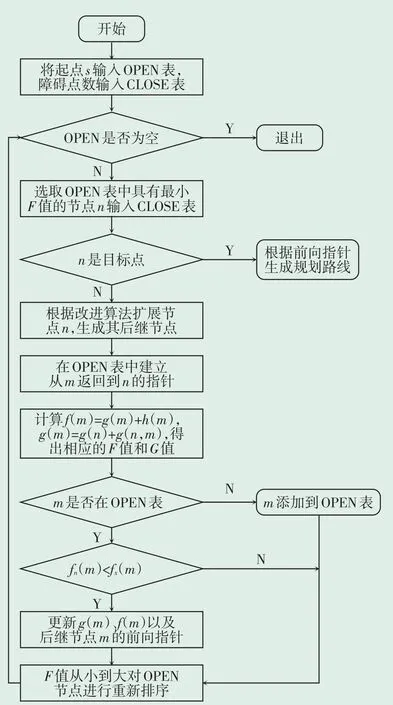
图4 16邻域A*算法路径规划流程

（1）模拟变电站的路径信息，建立如图5所示的基于栅格地图的工作环境空间，蓝色边框为当前变电站的边界，蓝色不规则图形代表变电站中的障碍物，白色代表可通行路径，区域长度为300单元格，宽度为200单元格。

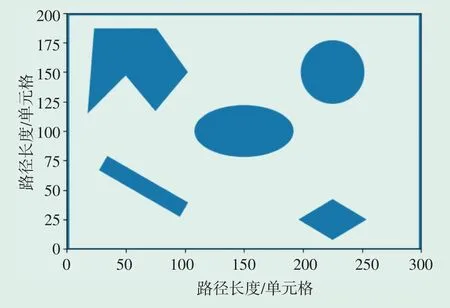
图5 模拟变电站栅格图

（2）在数据空间中建立OPEN和CLOSE表，以最小二叉堆的形式在OPEN表中纳入堆顶点为s，CLOSE表内用数值表示存储障碍点，以表明其为禁止通过区域。

（3）根据16邻域A*算法对每个输入点为中心的两层邻接点进行判断。首先判断其是否为障碍点或已经存在于OPEN表中的点，若既不是障碍点也不是OPEN表中已有的点，则采用最小二叉堆的存储方式加入到OPEN表中，以节点的F值作为排列父子节点顺序的规则，每个父节点的F值都比其子节点的F值小，采用这种方式存储时，每次在堆顶的节点有可能成为最优路径上的节点；若其为障碍点或已经存在于CLOSE表中，则跳过该点；若其不是障碍点且在OPEN表中，则比较该节点与其父节点的G值，取G值小的点作为新的父节点，并重新计算G值和F值。

（4）取出OPEN表中F值最小的节点加入到CLOSE表中，即将根节点加入CLOSE表中。判断当前节点是否为目标节点，若为目标节点，则最优解找到，否则判断OPEN表是否为空，若为空，则路径不存在；若不为空，则扩展当前节点并生成后继节点，返回步骤3继续判断。

3 试验与结果

3.1 环境配置

在PyCharm COMMUNITY 2019.2环境中，创建长度为300单元格，宽度为200单元格的栅格图，内部包含60 000个顶点，59 501个栅格。试验中主机配置为Intel Core i7-8565U CPU@1.8 GHz，内存为8 GB，16邻域A*算法通过Python编程实现。路径规划结果使用Python进行绘图展示。

3.2 对比试验

为验证基于16邻域A*算法对于路径规划的有效性，使用传统A*算法与16邻域A*算法进行对照试验，在一张300单元格×200单元格栅格地图上，通过设置4个不同的终点，进行4组对比试验。为避免试验过程中产生随机误差，每组试验数据由5次重复试验的平均值得出。本次试验过程中，4组试验的起点位置均为（50，30），终点位置的横坐标按照从左至右、纵坐标按照从下至上依次增加的方式进行组合，最终得到相应的终点位置，如表1所示。

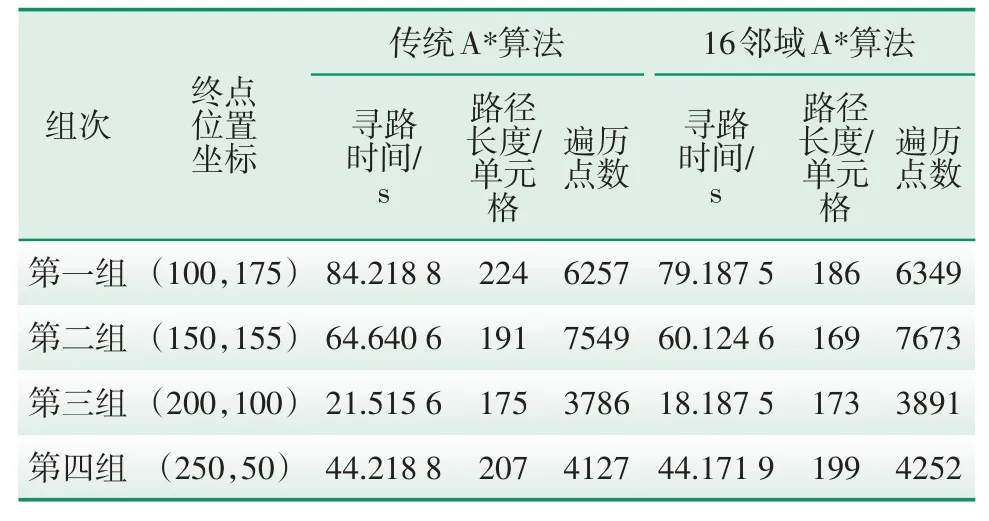
表1 传统A*算法与16邻域A*算法路径规划效果对比

由第一组和第四组试验可以看出，路径上障碍物越多，寻路时间越长，符合客观规律。在寻路时间较长的路径中，16邻域A*算法在寻路效率方面更有优势。比如，在第一组和第二组试验中，由于路径上障碍物较多，寻路时间均超过50 s，16邻域A*算法的寻路时间较传统A*算法节约4 s的时间；而寻路时间较短的路径中，两种算法的寻路效率相近，如第三组和第四组试验中，两种算法的寻路时间和最终获得的最优路径在数值上趋近，差距较小。16邻域A*算法的遍历点数较传统A*算法多，因为16邻域A*算法在OPEN表中加入了更多的候选节点，使路径可选方向得到进一步扩展。在最优路径的寻找过程中，16邻域A*算法能够在更短的时间内找出更优的路径，尤其在寻路时间较长的路径上更明显。

图6—图9为传统A*算法与16邻域A*算法路径规划对比图。图中包含了4组试验中两种算法各自选出的最优路径。可以看出，传统A*算法在解决移动机器人路径规划时，由于受到了运动方向的限制，导致规划处的路径转折点比较复杂、转折次数较多，最终得到的路径不够平滑，而且规划出的路径长度也不是最优，而16邻域A*算法在路径的转折点个数、路径平滑性等指标上都有所改进。

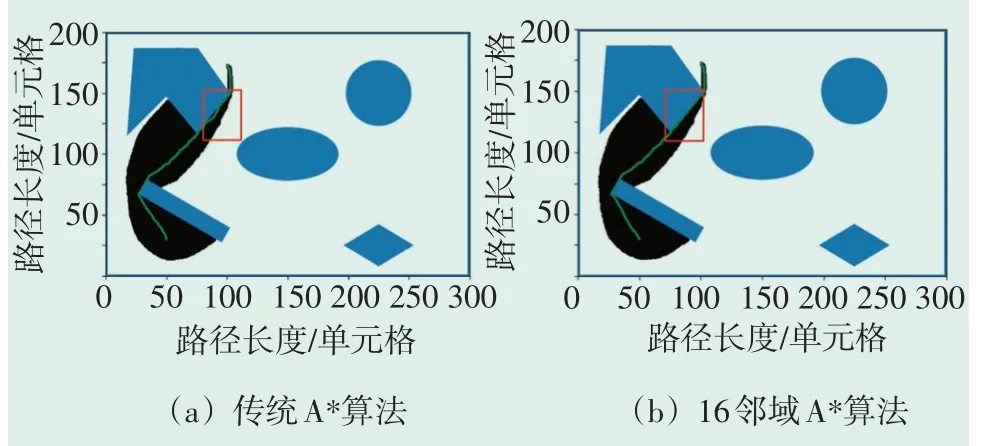
图6 第一组试验对比图

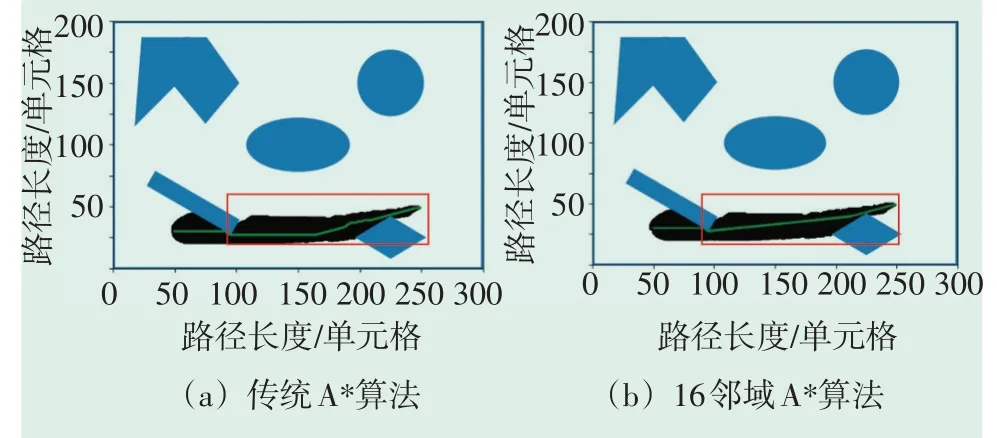
图9 第四组试验对比图

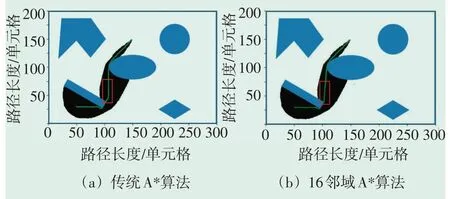
图7 第二组试验对比图

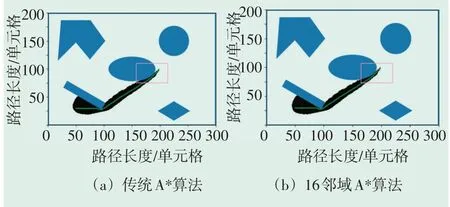
图8 第三组试验对比图

4 结束语

本文针对传统A*算法在路径规划时可能出现规划路径长度不是最优、路径不够平滑等问题，提出采用16邻域A*算法对每个输入点为中心的两层所有邻接点进行判断，使得A*算法在进行路径规划时，路径方向的选择不再受限于π/4的整数倍。同时，采用最小二叉堆对OPEN表中的候选节点进行存储，使算法整体复杂度变小。新算法在提高路径规划平滑性上有较好效果，同时保证了算法的效率，为解决变电站巡检路径规划问题提供了新的思路。