基于RBF网络模糊推理的火电厂主汽温PID串级控制系统
2022-01-07杨科科任宁宁
杨科科 任宁宁
(河南工业职业技术学院 河南南阳 473400)
现代火电厂中的锅炉都是在高温、高压下进行工作的,锅炉过热器出口的过热蒸汽温度是衡量蒸汽品质的重要指标。因此,主汽温是锅炉运行中必须监视和控制的主要参数之一。
目前,火力发电机组广泛采用PID串级控制方式控制过热蒸汽温度。虽然PID控制结构简单,精确度高,易于操作并且具有强鲁棒性,但是由于主汽温对象具有大延迟、大惯性、非线性时变等特点,尤其是随着机组容量和参数的提高,蒸汽过热的受热面比例加大,使其迟延和惯性更大,从而进一步加大了控制难度[1]。当负荷发生变化时,主蒸汽温度的动态特性变化明显,参数和结构变化较大。因此,常规PID控制器很难满足这种大惯性、大延迟和非线性时变系统的控制需要。
模糊控制和神经网络是智能控制的两个重要分支,两者虽然在概念、内涵上有着明显的不同,但都是为了处理实际系统中的不确定性、不精确性等引起的用常规PID控制方法难以解决的问题,现在倍受瞩目的方法是将模糊控制与神经网络相结合,形成模糊神经网络。模糊神经网络不仅在结构上具有明显的模糊推理意义,而且具有较常规PID控制算法更强的非线性逼近能力,并且采用分布数据处理方法使大量的实时控制运算成为可能,因此具有更优越的控制性能[2]。RBF网络具有收敛速度快,逼近能力强,训练周期短,网络结构易于调整的优点[3]。基于RBF网络模糊推理的PID串级控制系统,不但具有常规PID控制系统的优良特性,又具有模糊神经网络控制系统的自适应、自学习能力,这种智能控制系统在不同工况变化情况下,对大惯性、大延迟和非线性时变的主汽温对象具有较常规PID控制系统更优越的控制性能。
1 基于RBF网络模糊推理的主汽温PID串级控制系统
基于RBF网络模糊推理的主汽温PID串级控制,采用过热汽温双回路调节系统,如图1所示。内回路采用比例控制,充分利用串级控制副调节器消除内扰的优点,主要是消除减温水扰动。外回路采用基于RBF网络模糊推理的PID串级控制,用RBF网络实现模糊推理,利用模糊控制和优化指标来调节PID控制器的参数。为了尽量简化控制系统实现的复杂性,同时充分利用串级控制副调节器消除内扰的优点,将串级控制中的内回路和主汽温对象的惰性区 合并为广义被控对象(Generalized Plant)。由于惰性区是主汽温系统的主要特性所在,此广义被控对象仍然是随机组负荷变化的多模型系统[4]。
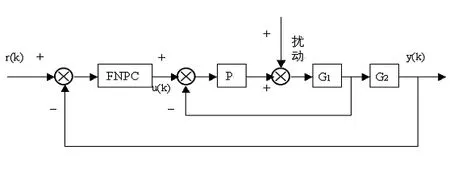
图1 基于RBF网络模糊推理的PID串级主汽温控制系统结构图
其中,FNPC为基于RBF网络模糊推理的PID串级控制系统,P为内回路比例控制器。r(k)为给定信号;u(k)为 FNPC 输出;y(k)为系统输出;G1、G2分别为主汽温对象惰性区和导前区传递函数。
2 基于RBF网络的模糊PID控制器设计
2.1 基于 RBF网络的模糊PID控制器参数模糊化
RBF网络输入变量的个数越多,控制精度越高,但是个数过多,模糊控制规则变得过于复杂,模糊推理的实现就相当困难[5]。所以根据RBF网络模糊推理PID控制器的结构,选用误差 e(k)和误差变化率∆e(k) 作为模糊神经网络控制器的输入变量,KP、KI、KD为输出变量。
误差e(k) 和误差变化率∆e(k) 的模糊子集均定义为:
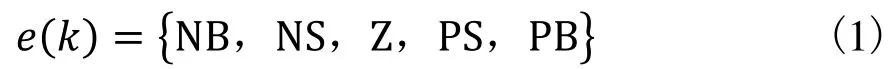
式中:NB =“负大”,NS =“负小”,Z =“零”,PS=“正小”,PB =“正大”。
∆e(k)模糊子集的定义与e(k)类似,故此处略去。
KP、KI、KD的模糊子集定义为:

式中:Z=“零”,S=“小”,M=“中”,B=“大”。
KI与KD模糊子集的定义与KP类似,故此处略去。
设定误差 e(k) 和误差变化率∆e(k)的论域为[-3,3],KP的论域为[0,10],KI与KD的论域为[0,2]。把e(k) 和∆e(k) 的论域[-2,2]之间变化的连续量离散化为五个等级,分别表示为:-2,-1,0,1,2,即:
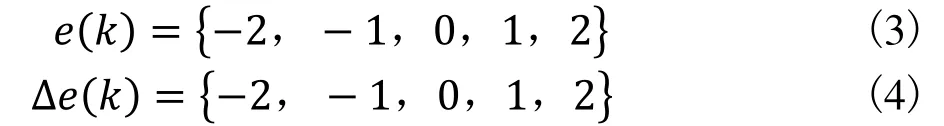
把KP、KI、KD的论域离散化为四个等级,采用高斯函数为隶属度函数。
误差e(k)和误差变化率∆e(k)作为模糊神经网络的输入变量经模糊化以后,将模糊子集论域中的元素作为输入数据训练RBF网络以实现模糊推理。
2.2 模糊控制规则设计
模糊控制规则基于手动控制策略设计,尽管影响锅炉过热汽温的因素很多,但按照操作人员的经验有如下控制原则:
(1)当e(k)较大时,增大KP,减小KD,KI取值最小。
(2)当e(k)大小中等时,应减小KP,KI取大小中等。
(3)当e(k) 较小时,应减小KP与KI。
(4)当∆e(k) 较大时,应减小KD。
(5)当∆e(k) 较小时,应增大 KD。
根据以上原则,并对操作人员的实际操作步骤进行详细分析,可得KP、KI、KD模糊控制规则表如表1所示。

表1 KP、KI 、KD模糊控制规则表
KP的特性曲面如下图2所示,KI和KD的特性曲面与KP类似,此处略去。
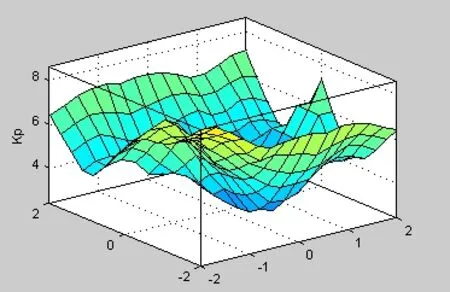
图2 的特性曲面
3 RBF网络对模糊推理的实现
3.1 RBF网络模型
1985年,Powell提出了多变量插值的径向基函数(Radial Basis Function—RBF)。1988年,Broomhead和Lowe首先将RBF应用于神经网络设计,从而构成 RBF神经网络。RBF网络是一种三层前向网络,由输入层、隐含层以及输出层组成。隐含层单元的变换函数是RBF,它是一种局部分布的对中心点径向对称衰减的非负非线性函数[6]。RBF网络结构如图3所示。
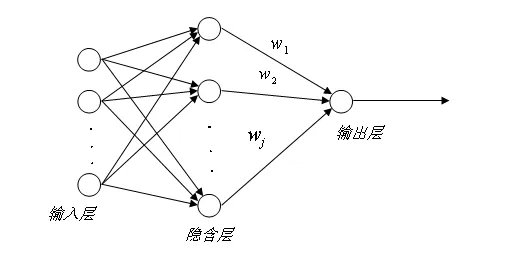
图3 RBF网络结构
在 RBF 网络结构中,X= [x1,x2,…,xn]T为网络的输入向量。RBF网络的径向基向量H=[h1,h2,…,hj…,hmT,其中hj高斯基函数
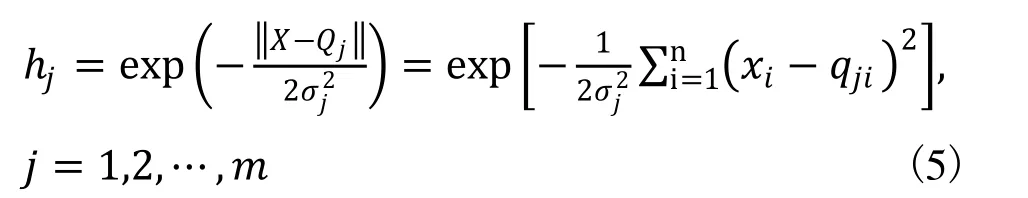
网络的第j个节点的中心矢量即高斯函数的中心为:Qj=[qj1,qj2,…,qji,…qjnT,其中,i=1,2,…,n
设网络的基宽向量即高斯函数的方差为:σ=[σ1,σ2,…,σm]T,σj为节点j的基宽度参数,且为大于零的数。
网络的权向量为w= [w1,w2,…,wm]T。
RBF网络的输出为:
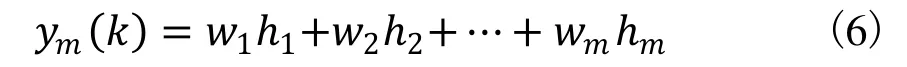
RBF网络性能指标函数为[7]:
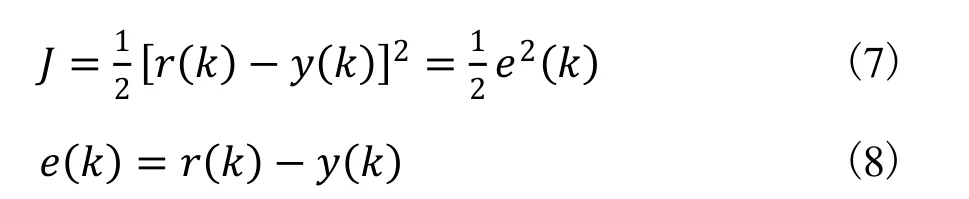
依最速下降法修正网络的权值wj,即按J对权值的负梯度方向搜索调整,并附加一使搜索快速收敛全局极小的惯性项。高斯函数的中心qj和σj方差 也可采用与wj类似的学习算法求出,则有:
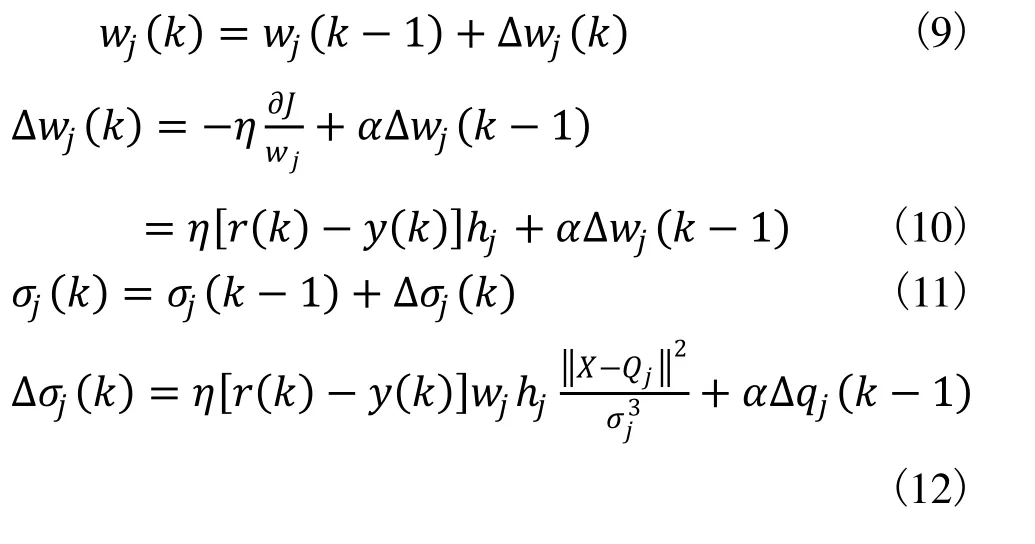
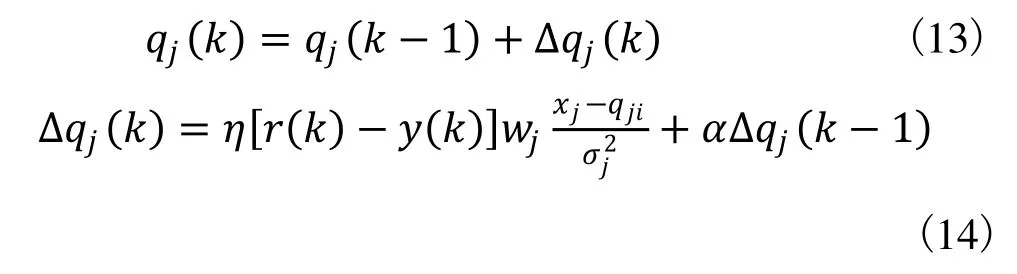
式中:η为学习速率;α为惯性系数。
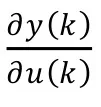
3.2 模糊推理的实现
采用 RBF网络构成模糊神经网络的最大优势在于RBF网络和模糊推理过程的函数等价性。根据等价性,将两种不同结构的系统在函数上统一起来。
本文所用模糊控制系统,其模糊规则可以表示为:
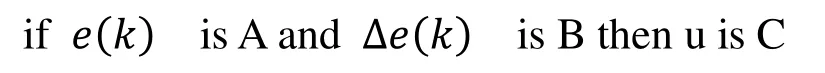
e(k)、∆e(k)、u 分别表示为误差、误差变化率、控制量输出,A、B、C分别为相应论域上的模糊子集。
采用模糊关系合成法作为推理算法,并且在模糊推理算法中取各隶属度函数为高斯函数,则规则的合成函数可以写成
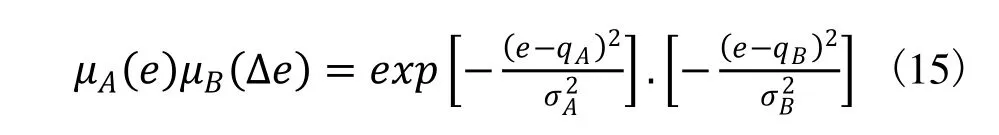
由上式和高斯函数相比较可以看出,模糊推理过程和RBF网络具有内在的相似性,当模糊规则的个数和RBF中心值的个数相等时,两式是一致的,即在函数上是等价的。从模糊知识的表达观点看,RBF网络本质上是“if„then„”规则的网络表达形式,其每一个隐含层节点映射了一条模糊规则。
4 仿真研究
为了进一步检验本文提出的基于 RBF网络模糊推理的PID串级控制系统对火电厂主汽温对象控制的优越性能,选用某火电厂锅炉过热汽温控制对象的动态特性[8],并借助 MATLAB中的 simulink进行了仿真研究。
主汽温对象导前区传递函数为:
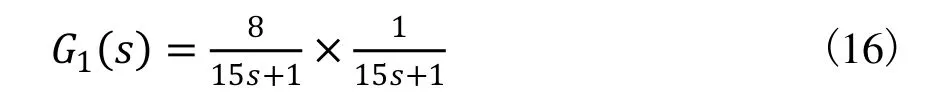
主汽温对象惰性区传递函数为:
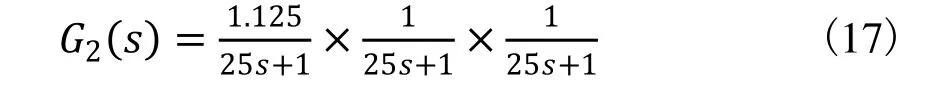
在串级过热汽温控制系统中,内回路能迅速的消除减温水的自发性扰动和其他进入内回路的各种扰动,副调节器一般采用P调节器对过热汽温的稳定起“粗调”作用[9],外回路则采用基于RBF网络模糊推理的PID串级控制器,取2输入1输入,含25个隐含神经元的RBF模糊神经网络。内回路P调节器的比例系数取:KP=9,RBF网络的学习速率η 和惯性系数α 分别取:η=0.35,α=0.02,则基于RBF网络模糊推理的PID串级控制系统阶跃响应曲线如图 4中曲线 1所示。 火电厂主汽温常规PID 串级控制系统取:KP=0.6,KI=0.01, KD=0.8,内回路P调节器的比例系数取:KP=9,则常规PID控制系统阶跃响应曲线如图4中曲线2所示。
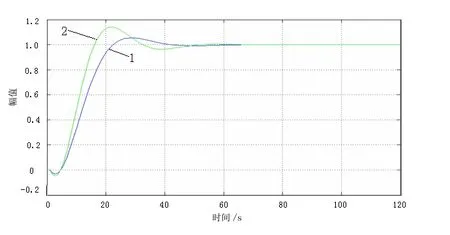
图4 系统阶跃响应曲线比较
从上述两组仿真曲线可以看出本文提出的控制策略与常规PID控制相比,具有调节速度快,超调量小及鲁棒性能强等优点。
5 结语
鉴于火电厂主汽温对象的大惯性、大延迟和非线性时变等特性,本文提出了基于RBF网络实现模糊推理的PID串级控制策略。从仿真结果可以看出,基于RBF网络模糊推理的PID串级控制与常规PID控制相比,调节更为平稳、速度更快,超调量减小。这说明本文提出的用RBF网络实现模糊推理的PID串级控制,提高了控制系统的适应能力和鲁棒性,改善了系统的动、静态品质和稳定性。
