基于双论域信息系统的三支决策增量式更新算法
2021-03-16袁路妍
袁路妍 李 锋
1(绍兴职业技术学院信息工程学院 浙江 绍兴 312000) 2(东华大学计算机科学与技术学院 上海 200051)
0 引 言
三支决策模型[1]是由著名学者Yao提出的一种新的决策模型,它由决策粗糙集进行诱导得出,通过一对阈值将整个论域空间分成三个不相交的区域,这三个区域对应着三种决策结果,即接受、延迟和拒绝[1-2]。目前三支决策模型已成功运用于多种工程应用中[3-6]。
继Yao提出三支决策之后,学者们不断对其进行改进和推广,使得该模型适用于更为复杂的数据环境和更为广泛的应用场景。传统的三支决策模型建立在完备的信息系统中,为了扩大适用范围,Liu等[7]在不完备信息系统的基础上提出了一种改进的三支决策。针对数值型的数据,Li等[8]将传统的三支决策模型推广至邻域空间,提出了邻域三支决策模型。在模糊环境下,Deng等[9]提出了基于模糊集的三支决策。Liang等[10]在直觉模糊集下诱导出了多种策略的三支决策模型。Zhao等[11]在模糊区间值信息系统下定义了三支决策。同时在其他模型中,学者们也做出了大量的改进与推广。Qian等[12]在多粒度粗糙集中融入了三支决策模型。Lin等[13]学者在Qian等的基础上提出了模糊环境下的多粒度三支决策。在多个代价函数方面,Dou等[14]提出了多代价策略的三支决策。对于多分类情形,Zhou[15]提出了多类情形的三支决策。总之在其他各类的理论模型中,三支决策模型已经成为较为热门的研究内容[16-18]。
在数据挖掘领域,双论域信息系统是一种重要的数据形式[19],它常见于推荐系统中。对于这种类型的数据,Sun等[20-21]提出了一种推广的三支决策模型,即双论域三支决策。在该模型的基础上,学者们又进行了多种推广和应用[22-23],例如Huang等[23]提出了基于三支决策的个性化推荐算法。关于双论域信息系统的三支决策也是目前的一个研究热点。
然而,实际中的数据总是不断动态更新的,这给传统模型和算法的实际应用带来了一定的挑战。解决这类问题的主要方法是进行增量式学习,针对三支决策模型,目前已有一些相关的增量式算法被提出[24-27],例如Luo等[27]提出了一种矩阵方法的三支决策动态更新。遗憾的是,在这些已有的研究成果中,还未有对双论域信息系统下的三支决策模型进行增量式更新的相关研究,因此促使本文对这方面的问题进行探索。
为了弥补双论域信息系统下三支决策模型关于增量式更新研究的空白,本文提出一种高效的增量式更新算法。首先分别研究了双论域信息系统下两个论域动态更新时,三支决策模型中三个区域的增量式更新问题,理论证明了这种增量更新只依赖于变化的数据。然后基于这种更新机制,提出对应的增量式更新算法。最后通过进行一系列的仿真实验验证了所提出增量式算法的有效性。
1 基本理论
定义1[20]设双论域信息系统可表示为S=(U,V),其中U和V为该信息系统下的两个论域。记F为从U到V上的二元关系,对于u∈U和v∈V,若它们满足二元关系F,即(u,v)∈F,并且u和v存在如下映射关系:
F(u)={v∈V|(u,v)∈F}u∈UF-1(v)={u∈U|(u,v)∈F}v∈V
(1)
定义2[20]设双论域信息系统S=(U,V)以及U和V上确定的二元关系F,那么对于Y⊆V关于二元关系F的下近似和上近似分别定义为:

(2)

(3)
在三支决策模型中,通常研究三种动作行为的决策问题。对于Y=Yj,那么Yc=V-Yj,即状态集可表示为Ω={Y,Yc},行为集包含三种动作,即A={dP,dB,dN},分别代表了接受、延迟和拒绝三种决策。根据贝叶斯决策过程,对于u∈U可以诱导出如下最小代价规则:
(1) 当P(Y|F(u))≥α且P(Y|F(u))≥γ, 决策POS(Y)。
(2) 当P(Y|F(u))≤α且P(Y|F(u))≥β,决策BUN(Y)。
(3) 当P(Y|F(u))≤β且P(Y|F(u))≤γ,决策NEG(Y)。
其中:
(4)
由于代价通常满足特定的关系[1-2],这使得阈值通常满足0≤β<γ<α≤1。对于Y⊆U可以得到在二元关系F下关于阈值α、β的三个区域:
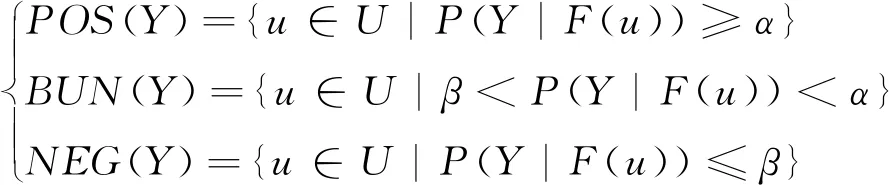
(5)
这三个区域直接对应三支决策模型中的三个决策规则[1],即正区域POS(Y)中的对象接受Y决策,边界域BUN(Y)中的对象延迟Y决策,负区域NEG(Y)中的对象拒绝Y决策。因此对于双论域信息系统下的三支决策模型,即需要得到决策对象集关于给定α、β阈值的三个区域[20]。
2 双论域下三支决策的动态更新
由于现实环境下数据的动态性,双论域信息系统往往处于不断动态更新之中,因此本节主要研究双论域信息系统动态变化后三支决策的动态更新问题。由于双论域的动态更新涉及到两个论域的变化,因此分别对每个论域进行单独分析。
2.1 论域U变化时三支决策的动态更新
2.1.1对象增加时模型的更新
根据第1节,三支决策规则的诱导主要取决于三个区域的计算,因此当信息系统发生变化后,研究三支决策的动态更新即转换为研究三个区域的动态更新。
设t时刻的双论域信息系统表示为St=(Ut,Vt),Ut和Vt确定的二元关系为Ft,对于Yt⊆Vt在Ft下关于阈值α、β确定的三个区域分别表示为POS(Yt)、BUN(Yt)和NEG(Yt)。t+1时刻双论域信息系统更新为St+1=(Ut+1,Vt+1),其中:Ut+1=Ut∪U+;Vt+1=Vt;此时Ut+1和Vt+1确定的二元关系为Ft+1。对于Yt+1=Yt在Ft+1下关于阈值α、β确定的三个区域表示为POS(Yt+1)、BUN(Yt+1)和NEG(Yt+1)。
定理1设0≤β<α≤1,t时刻Yt⊆Vt关于二元关系Ft的三个区域为POS(Yt)、BUN(Yt)和NEG(Yt)。那么t+1时刻Yt+1关于二元关系Ft+1的三个区域增量式更新为:
(1)POS(Yt+1)=POS(Yt)∪Δ,其中:
Δ={u∈U+|P(Yt+1|Ft+1(u))≥α}
(2)BUN(Yt+1)=BUN(Yt)∪Δ,其中:
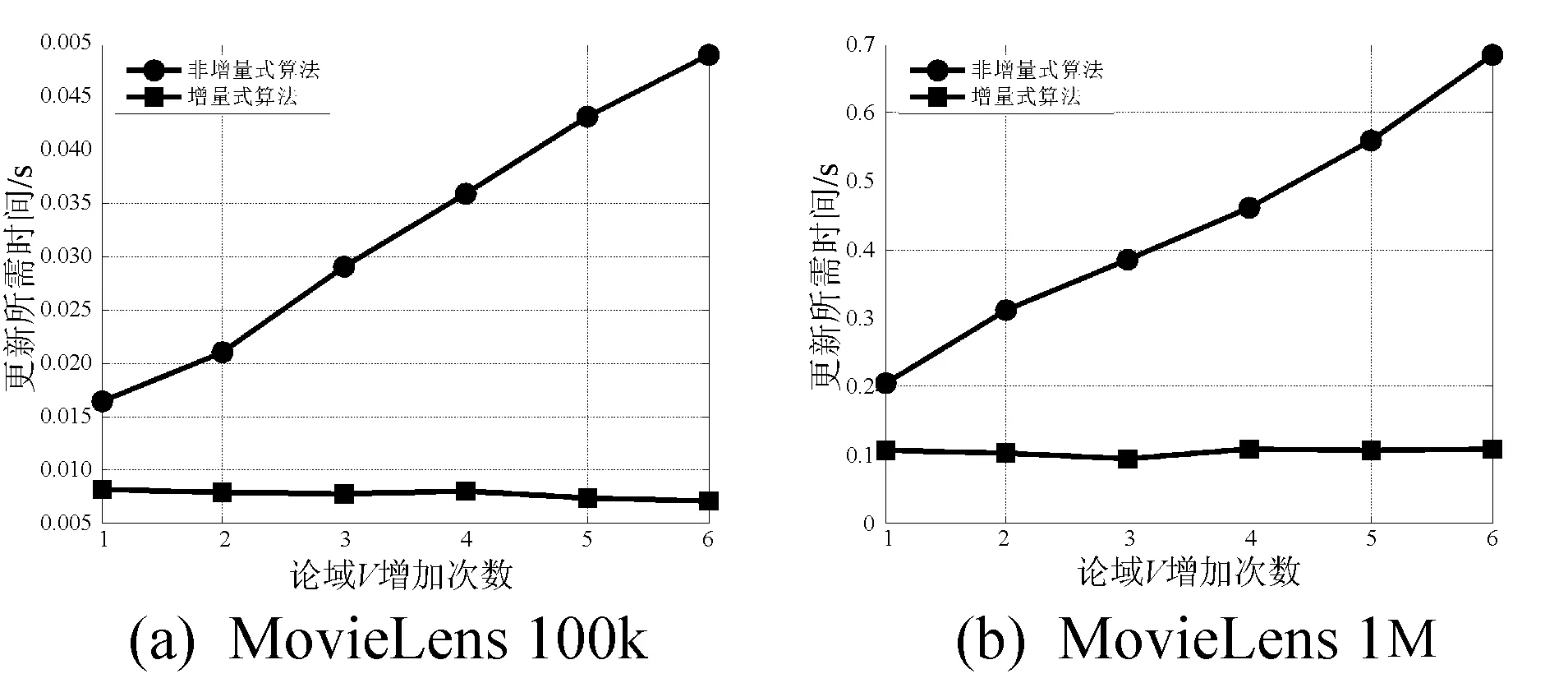
Δ={u∈U+|β (3)NEG(Yt+1)=NEG(Yt)∪Δ,其中: Δ={u∈U+|P(Yt+1|Ft+1(u))≤β} 证明: (1) 根据正区域的定义有: POS(Yt+1)={u∈Ut+1|P(Yt+1|Ft+1(u))≥α}= {u∈Ut∪U+|P(Yt+1|Ft+1(u))≥α}= {u∈Ut|P(Yt+1|Ft+1(u))≥α}∪ {u∈U+|P(Yt+1|Ft+1(u))≥α} 对于∀x∈Ut,即Ft+1(u)=Ft(u),又由于Yt+1=Yt,所以P(Yt+1|Ft+1(u))=P(Yt|Ft(u)),u∈Ut。则{u∈Ut|P(Yt+1|Ft+1(u))≥α}=POS(Yt),所以POS(Yt+1)=POS(Yt)∪Δ,其中:Δ={u∈U+|P(Yt+1|Ft+1(u))≥α} (2)和(3)的证明类似于(1)。 证毕。 通过定理1可以发现,当论域U增加对象集U+后,只需要对增加的对象计算相应的三个区域,然后与原来三个区域进行合并便可以更新出最终结果。 2.1.2对象减少时模型的更新 类似于2.1.1节的探究思路,这里同样可以得到论域U中对象减少时三个区域的增量式更新问题。 设t时刻的双论域信息系统表示为St=(Ut,Vt),Ut和Vt确定的二元关系为Ft,对于Yt⊆Vt在Ft下关于阈值α、β确定的三个区域分别表示为POS(Yt)、BUN(Yt)和NEG(Yt)。t+1时刻双论域信息系统更新为St+1=(Ut+1,Vt+1),其中:Ut+1=Ut-U-;Vt+1=Vt;此时Ut+1和Vt+1确定的二元关系为Ft+1。对于Yt+1=Yt在Ft+1下关于阈值α、β确定的三个区域表示为POS(Yt+1)、BUN(Yt+1)和NEG(Yt+1)。 定理2设0≤β<α≤1,t时刻Yt⊆Vt关于二元关系Ft的三个区域为POS(Yt)、BUN(Yt)和NEG(Yt)。那么t+1时刻Yt+1关于二元关系Ft+1的三个区域增量式更新为: (1)POS(Yt+1)=POS(Yt)-Δ,其中: Δ={u∈U-|u∈POS(Yt)} (2)BUN(Yt+1)=BUN(Yt)-Δ,其中: Δ={u∈U-|u∈BUN(Yt)} (3)NEG(Yt+1)=NEG(Yt)-Δ,其中: Δ={u∈U-|u∈NEG(Yt)} 证明: (1) 根据正区域的定义有: POS(Yt+1)={u∈Ut+1|P(Yt+1|Ft+1(u))≥α}= {u∈Ut-U-|P(Yt+1|Ft+1(u))≥α}= {u∈Ut|P(Yt+1|Ft+1(u))≥α}- {u∈U-|P(Yt+1|Ft+1(u))≥α} 对于∀x∈Ut,即Ft+1(u)=Ft(u)。又由于Yt+1=Yt,所以: {u∈Ut|P(Yt+1|Ft+1(u))≥α}=POS(Yt) 由于U-⊆Ut,所以: {u∈U-|P(Yt+1|Ft+1(u))≥α}⊆POS(Yt) 则POS(Yt+1)=POS(Yt)-Δ,其中: Δ={u∈U-|u∈POS(Yt)} (2)和(3)的证明类似于(1)。 证毕。 通过定理2可以发现,当论域U减少一部分对象U-,只需要对原来三个区域中的对象作出相应的删除便可以更新出最终结果。 2.2.1对象增加时模型的更新 设t时刻的双论域信息系统表示为St=(Ut,Vt),Ut和Vt确定的二元关系为Ft,对于Yt⊆Vt在Ft下关于阈值α、β确定的三个区域分别表示为POS(Yt)、BUN(Yt)和NEG(Yt)。t+1时刻双论域信息系统更新为St+1=(Ut+1,Vt+1),其中:Ut+1=Ut;Vt+1=Vt∪V+;此时Ut+1和Vt+1确定的二元关系为Ft+1且Ft+1=Ft∪F+,显然F+是论域Ut和V+确定的二元关系。对于Yt+1=Yt∪Y+(Y+⊆V+)在Ft+1下关于阈值α、β确定的三个区域分别表示为POS(Yt+1)、BUN(Yt+1)和NEG(Yt+1)。 定理3对于∀u∈Ut,设Yt关于u在二元关系Ft下的条件概率为P(Yt|Ft(u)),双论域信息系统更新后,Yt+1=Yt∪Y+关于对象u在二元关系Ft+1下的条件概率为P(Yt+1|Ft+1(u))。则: (1) 若P(Y+|F+(u))≥P(Yt|Ft(u)),那么: P(Yt|Ft(u))≤P(Yt+1|Ft+1(u))≤P(Y+|F+(u)) (2) 若P(Y+|F+(u))≤P(Yt|Ft(u)),那么: P(Y+|F+(u))≤P(Yt+1|Ft+1(u))≤P(Yt|Ft(u)) 式中:P(Y+|F+(u))表示Y+关于u在二元关系F+下的条件概率。 证明:根据定义有: 这里令: |Yt∩Ft|=a,|Y+∩F+|=a+,|Ft|=b,|F+|=b+ 那么: 则有: 所以: P(Y+|F+(u))≥P(Yt+1|Ft+1(u)) P(Yt|Ft(u))-P(Yt+1|Ft+1(u))= 所以: P(Yt|Ft(u))≤P(Yt+1|Ft+1(u)) 综上有: P(Yt|Ft(u))≤P(Yt+1|Ft+1(u))≤P(Y+|F+(u)) (2) 的证明过程类似于(1)。 证毕。 定理3表明,当双论域信息系统更新后,P(Yt+1|Ft+1(u))值始终介于P(Yt|Ft(u))与P(Y+|F+(u))之间,根据条件概率这一变化规律,可以进一步得到论域V中对象增加时三个区域的增量式更新。 定理4设0≤β<α≤1,t时刻Yt⊆Vt关于二元关系Ft的三个区域为POS(Yt)、BUN(Yt)和NEG(Yt)。那么t+1时刻Yt+1关于二元关系Ft+1的三个区域增量式更新为: 1) ∀u∈POS(Yt),那么: (1) 若P(Y+|F+(u))≥α,则u∈POS(Yt+1)。 (2) 若P(Y+|F+(u))<α,则: 2) ∀u∈BUN(Yt),那么: (1) 若β (2) 若P(Y+|F+(u))≥α,则: (3) 若P(Y+|F+(u))≤β,则: 3) ∀u∈NEG(Yt),那么: (1) 若P(Y+|F+(u))≤β,则u∈NEG(Yt+1)。 (2) 若P(Y+|F+(u))>β,则: 证明: (1) 对于∀u∈POS(Yt),有P(Yt|Ft(u))≥α。 若P(Y+|F+(u))≥α,根据定理3满足: P(Yt+1|Ft+1(u))≥α 因此u∈POS(Yt+1)。 若P(Y+|F+(u))<α,根据定理3可知P(Yt+1|Ft+1(u))的值介于P(Yt|Ft(u))和P(Y+|F+(u))之间,因此P(Yt+1|Ft+1(u))的值无法确定,所以此时需要分开讨论,则有: 因此(1)成立。 (2)和(3)的证明过程类似于(1)。 证毕。 定理4表明,当双论域信息系统论域V中的对象动态增加后,需要对对象u∈U计算条件概率P(Y+|F+(u)),当该条件概率与阈值α、β满足某些特定关系时,可以直接判定出u隶属于哪个区域。对于条件概率与阈值α、β不满足特定关系时,这时才需要计算对象u的新条件概率P(Yt+1|Ft+1),然后根据新的条件概率判定该对象的区域隶属情况,同时新条件概率的计算可采用增量式的方式,即: 因此,按定理4的更新方式具有较高的计算效率。 2.2.2对象减少时模型的更新 设t时刻的双论域信息系统表示为St=(Ut,Vt),Ut和Vt确定的二元关系为Ft,对于Yt⊆Vt在Ft下关于阈值α、β确定的三个区域分别表示为POS(Yt)、BUN(Yt)和NEG(Yt)。t+1时刻双论域信息系统更新为St+1=(Ut+1,Vt+1),这里的Ut+1=Ut,Vt+1=Vt-V-,此时Ut+1和Vt+1确定的二元关系为Ft+1,且Ft+1=Ft-F-,显然F-是论域Ut和V-确定的二元关系。对于Yt+1=Yt-Y-(Y-⊆V-)在Ft+1下关于阈值α、β确定的三个区域表示为POS(Yt+1)、BUN(Yt+1)和NEG(Yt+1)。 定理5对于∀u∈Ut,设Yt关于u在二元关系Ft下的条件概率为P(Yt|Ft(u)),双论域信息系统更新后,Yt+1=Yt-Y-关于对象u在二元关系Ft+1下的条件概率为P(Yt+1|Ft+1(u))。则: (1) 若P(Y-|F-(u))≥P(Yt|Ft(u)),则: P(Yt+1|Ft+1(u))≤P(Yt|Ft(u)) (2) 若P(Y-|F-(u))≤P(Yt|Ft(u))则: P(Yt|Ft(u))≤P(Yt+1|Ft+1(u)) 证明:根据定义有: 这里令: |Yt∩Ft|=a,|Y-∩F-|=a-,|Ft|=b,|F-|=b- 那么: 则有: P(Yt|Ft(u))-P(Yt+1|Ft+1(u))= 所以P(Yt+1|Ft+1(u))≤P(Yt|Ft(u))。 (2) 的证明过程类似于(1)。 证毕。 根据定理5所示的条件概率变化关系,可以得到当论域V中对象减少时三支决策中三个区域的增量式更新。 定理6设0≤β<α≤1,t时刻Yt⊆Vt关于二元关系Ft的三个区域为POS(Yt)、BUN(Yt)和NEG(Yt)。那么t+1时刻Yt+1关于二元关系Ft+1的三个区域增量式更新为: 1) ∀u∈POS(Yt),那么: (1) 若P(Y-|F-(u))≤P(Yt|Ft(u)),则u∈POS(Yt+1)。 (2) 若P(Y-|F-(u))≥P(Yt|Ft(u)),则: 2) ∀u∈BUN(Yt),那么: (1) 若P(Y-|F-(u))≤P(Yt|Ft(u)),则: (2) 若P(Y-|F-(u))≥P(Yt|Ft(u)),则: 3) ∀u∈NEG(Yt),那么: (1) 若P(Y-|F-(u))≥P(Yt|Ft(u)),则u∈NEG(Yt+1)。 (2) 若P(Y-|F-(u))≤P(Yt|Ft(u)),则: 证明过程类似于定理4。 定理6也表明,当双论域信息系统论域V中的对象动态减少后,需要对对象u∈U计算条件概率P(Y-|F-(u)),当该条件概率P(Y-|F-(u))满足某些特定关系时,可以直接判定出u隶属于哪个区域。对于条件概率不满足特定关系时,这时才需要计算对象u的新条件概率P(Yt+1|Ft+1),然后根据新的条件概率判定该对象的区域隶属情况,类似于定理4,新条件概率的计算同样可采用增量式的方式,即: 因此,按定理6的更新方式同样具有较高的计算效率。 本节给出双论域信息系统下三支决策的动态更新算法,首先给出非增量式的动态更新算法。根据文献[20],当双论域信息系统动态更新后,非增量式更新算法的主要思想是按照三个区域最基本的计算方式去更新三个区域,具体如算法1所示。 算法1[20]双论域信息系统下三支决策的非增量式更新算法 输入:新的双论域信息系统S=(Ut+1,Vt+1),阈值参数α、β和目标概念集Yt+1。 输出:POS(Yt+1),BUN(Yt+1),NEG(Yt+1)。 1.初始化POS(Yt+1)=∅,BUN(Yt+1)=∅,NEG(Yt+1)=∅。 2.对于∀u∈Ut+1,计算Yt+1关于对象u在二元关系Ft+1下的条件概率: 3.对于∀u∈Ut+1进行判断: ① 若P(Yt+1|Ft+1(u))≥α,则: POS(Yt+1)=POS(Yt+1)∪{u} ② 若β BUN(Yt+1)=BUN(Yt+1)∪{u} ③ 若P(Yt+1|Ft+1(u))≤β,则: NEG(Yt+1)=NEG(Yt+1)∪{u} 4.返回POS(Yt+1)、BUN(Yt+1)和NEG(Yt+1)。 在算法1所示的非增量式更新算法中,其主要的计算量集中在第2步中关于条件概率的计算,由于目标概念集Yt+1已经给定,条件概率的计算即为Ft+1(u)的计算,每个对象计算Ft+1(u)的时间复杂度为O(|Vt+1|),计算Ut+1中所有对象的时间复杂度为O(|Ut+1||Vt+1|)。因此整个算法1的时间复杂度为O(|Ut+1||Vt+1|)。 算法2所示的是双论域信息系统论域U中对象增加时三支决策的增量式更新算法。根据算法1,算法2的时间复杂度为O(|U+||Vt+1|)。 算法2双论域信息系统下三支决策的增量式更新算法(U增加) 输入:更新前后的双论域信息系统S=(Ut,Vt)和S=(Ut+1,Vt+1),其中Ut+1=Ut∪U+;阈值参数α、β和目标概念集Yt+1=Yt;POS(Yt)、BUN(Yt)和NEG(Yt)。 输出:POS(Yt+1),BUN(Yt+1),NEG(Yt+1)。 1.初始化: POS(Yt+1)=POS(Yt) BUN(Yt+1)=BUN(Yt) NEG(Yt+1)=NEG(Yt) 2.对于∀u∈U+,计算Yt+1关于对象u在二元关系Ft+1下的条件概率: 3.对于∀u∈U+进行判断: ① 若P(Yt+1|Ft+1(u))≥α,则: POS(Yt+1)=POS(Yt+1)∪{u} ② 若β BUN(Yt+1)=BUN(Yt+1)∪{u} ③ 若P(Yt+1|Ft+1(u))≤β,则: NEG(Yt+1)=NEG(Yt+1)∪{u} 4.返回POS(Yt+1)、BUN(Yt+1)和NEG(Yt+1)。 算法3所示的是双论域信息系统下论域U中对象减少时三支决策的增量式更新算法。在算法3中,只需要对U-中的对象进行考察分析便可以完成整个更新过程,因此算法3的时间复杂度为O(|U-|)。 算法3双论域信息系统下三支决策的增量式更新算法(U减少) 输入:更新前后的双论域信息系统S=(Ut,Vt)和S=(Ut+1,Vt+1),其中Ut+1=Ut-U-;阈值参数α、β和目标概念集Yt+1=Yt;POS(Yt)、BUN(Yt)和NEG(Yt)。 输出:POS(Yt+1),BUN(Yt+1),NEG(Yt+1)。 1.初始化 POS(Yt+1)=POS(Yt) BUN(Yt+1)=BUN(Yt) NEG(Yt+1)=NEG(Yt) 2.对于∀u∈U-进行以下判断: ① 若u∈POS(Yt),则: POS(Yt+1)=POS(Yt+1)-{u} ② 若u∈BUN(Yt),则: BUN(Yt+1)=BUN(Yt+1)-{u} ③ 若u∈NEG(Yt),则: NEG(Yt+1)=NEG(Yt+1)-{u} 3.返回POS(Yt+1)、BUN(Yt+1)和NEG(Yt+1)。 算法4所示的是双论域信息系统下论域V中对象增加时三支决策的增量式更新算法。在算法4中,主要的计算量集中在计算条件概率P(Y+|F+(u))上,对于部分条件概率P(Yt+1|Ft+1(u))可采用增量式方法计算得出,因此整个算法4的时间复杂度为O(|Ut+1||V+|)。 算法4双论域信息系统下三支决策的增量式更新算法(V增加) 输入:更新前后的双论域信息系统S=(Ut,Vt)和S=(Ut+1,Vt+1),其中Vt+1=Vt∪V+;阈值参数α、β和目标概念集Yt+1=Yt∪Y+;∀u∈Ut+1,条件概率P(Yt|Ft(u));POS(Yt)、BUN(Yt)、NEG(Yt)。 输出:POS(Yt+1),BUN(Yt+1),NEG(Yt+1)。 1.初始化POS(Yt+1)=∅,BUN(Yt+1)=∅,NEG(Yt+1)=∅。 2.对于∀u∈Ut+1计算P(Y+|F+(u)): ① 若u∈POS(Yt),当P(Y+|F+(u))≥α时u∈POS(Yt+1),否则根据P(Y+|F+(u))增量式计算出P(Yt+1|Ft+1(u)),然后判别u的隶属情况。 ② 若u∈BUN(Yt),当β ③ 若u∈NEG(Yt),当P(Y+|F+(u))≤β时u∈NEG(Yt+1),否则根据P(Y+|F+(u))增量式计算出P(Yt+1|Ft+1(u)),然后根据定理4判别u的隶属情况。 3.返回POS(Yt+1)、BUN(Yt+1)和NEG(Yt+1)。 算法5所示的是双论域信息系统下论域V中对象减少时三支决策的增量式更新算法,类似于算法4,算法5的时间复杂度为O(|Ut+1||V-|)。 算法5双论域信息系统下三支决策的增量式更新算法(V减少) 输入:更新前后的双论域信息系统S=(Ut,Vt)和S=(Ut+1,Vt+1),其中Vt+1=Vt-V-;阈值参数α、β和目标概念集Yt+1=Yt-Y-;∀u∈Ut,条件概率P(Yt|Ft(u));POS(Yt)、BUN(Yt)和NEG(Yt)。 输出:POS(Yt+1)、BUN(Yt+1)和NEG(Yt+1)。 1.初始化POS(Yt+1)=∅,BUN(Yt+1)=∅,NEG(Yt+1)=∅。 2.对于∀u∈Ut+1计算P(Y-|F-(u)): ① 若u∈POS(Yt),当P(Y-|F-(u))≤P(Yt|Ft(u))时u∈POS(Yt+1),否则根据P(Y-|F-(u))增量式计算出P(Yt+1|Ft+1(u)),然后判别u的隶属情况。 ② 若u∈BUN(Yt),那么根据P(Y-|F-(u))增量式计算出P(Yt+1|Ft+1(u)),然后判别u的隶属情况。 ③ 若u∈NEG(Yt),当P(Y-|F-(u))≥P(Yt|Ft(u))时u∈NEG(Yt+1),否则根据P(Y-|F-(u))增量式计算出P(Yt+1|Ft+1(u)),然后根据定理6判别u的隶属情况。 3.返回POS(Yt+1)、BUN(Yt+1)和NEG(Yt+1)。 本节将进行一系列实验来验证本文所提出增量式更新算法的有效性。表1给出了实验所使用的6个数据集,其中编号1至4的数据集为个性化推荐系统中常用的公开数据集,编号5和编号6给出了本文实验随机生成的人工数据集。本文实验所有的算法采用MATLAB 2014b进行编程实现,并且实验用计算机配置为CPU:Intel Core i5 4460 3.2 GHz, 内存:DDR3 16 GB 1 600 MHz。 表1 实验数据集 本文提出双论域信息系统下三支决策模型的动态更新算法,即双论域信息系统是不断动态更新的,而表1所示的均为静态数据集,因此本文实验采用文献[27]的处理方法,即让整个数据集均分成多个子数据集,然后通过逐个合并与分割的方式完成数据集的动态更新。将每个数据集按照论域U或论域V均分成7个子数据集,然后随机选择一份,不断让其他子数据集添加进行合并,这样构造出了6次动态增加更新,对于完整的数据集,每次移除一个子数据集,这样便构造出了6次动态减少更新。本文实验中所有算法都是基于该处理方式进行动态更新。 对于本文算法中的目标概念集Y,实验设定为随机选择当前论域V的四分之一对象,当论域V增加V+后,在V+中随机选择四分之一对象添加入Y中达到更新的效果。当论域V逐渐减小时,则按照相反的处理方式进行更新。在编号1至编号4的数据集中,其属性值为离散型,在编号5和编号6的人工数据集中,其属性值也为离散型,因此算法中的二元关系设定为等价关系。另外,算法中包含了参数α和参数β,在三支决策模型中,这两个参数由代价函数得出,因此本实验中令α=0.75,β=0.45。 本节针对论域U的动态变化,比较双论域三支决策的非增量式更新算法与增量式更新算法的更新效率。由于论域U的动态变化分为两种形式,因此分开进行实验。 图1是论域U中对象增加时,双论域三支决策在非增量式与增量式两类算法下的更新效率比较。 图1 各个数据集论域U增加时非增量式与增量式算法的更新效率比较 可以看出,随着数据集中论域U的不断增加更新,非增量式算法更新所需的时间也是不断增大的,并且增长的速率大致是线性的。而对于增量式更新算法,随着论域U的增大,其更新所需的时间基本上是保持不变的。出现这样的结果主要是由于其更新机制不同导致的,不同的机制有着不同的时间复杂度,从而表现出了很大的差异。对于非增量式更新算法,当论域U更新时,该算法在计算新数据集下三支决策仍然采用传统的计算方法,论域U增大,那么计算的时间也会增多。而增量式算法是对增加的数据进行计算,然后增量式更新得到新的模型结果,因此计算的时间只与增加的数据量有关,由于本文实验中数据集每次是均匀增加的,因此增量式算法每次的更新时间大致不变。可以看出,增量式算法比非增量式算法具有更高的更新效率。 图2为论域U中对象减小时,双论域三支决策在非增量式与增量式两类算法下的更新效率比较。 图2 各个数据集论域U减少时非增量式与增量式算法的更新效率比较 可以看出,随着论域U的逐渐减小,非增量式算法更新所需的时间是逐渐减小的,而增量式算法更新所需的时间非常少,几乎可以忽略。出现这种结果的主要原因同样是非增量式算法在更新时,需要对数据集进行重新计算,由于数据集的规模逐渐减小,因此所需的更新时间也是减小的。而对于增量式更新算法,定理2已经表明,只需对原来模型结果中的相关元素进行删除便可以完成更新,因此更新所需的时间极短,增量式更新算法的优势非常明显。 本节针对论域V的动态变化,比较双论域三支决策的非增量式更新算法与增量式更新算法的更新效率。同样地,由于论域V的动态变化分为两种形式,因此这里也需要分开进行实验。 图3是论域V中对象增加时,双论域三支决策在非增量式与增量式两类算法下的更新效率比较。 图3 各个数据集论域V增加时非增量式与增量式算法的更新效率比较 观察图3可以发现与图1具有类似的实验结果,即随着论域V的不断增大,非增量式算法更新时所需的时间不断增大,而增量式算法所需的更新时间大致保持不变,并且远小于非增量式算法。其主要原因同样是非增量式算法采用传统的计算,计算量与数据集的规模相关,规模越大计算量越大,而增量式算法只对新增加的数据进行相关计算,然后增量式地更新最终结果,因此计算时间只与新加入的数据量相关。所以增量式算法具有更高的更新效率。 图4是论域V中对象减少时,双论域三支决策在非增量式与增量式两类算法下的更新效率比较。 图4 各个数据集论域V减少时非增量式与增量式算法的更新效率比较 可以看出,随着论域V的不断减小,非增量式算法更新所需的时间也是不断减小的,而增量式算法所需的更新时间大致保持不变,并且远小于非增量式算法。其主要原因也是非增量式算法直接对数据集进行计算,当数据集论域V逐渐减小,因而计算时间也是逐渐减小。增量式算法只对减少的数据进行计算,然后在原来模型的结果上进行进一步更新,因此更新时所需的时间与减少的数据量相关,由于每次减少的数据量是一样的,因此增量式算法的更新时间保持不变。 综合两部分的实验结果可以看出,无论是论域U的动态更新还是论域V的动态更新,本文所提出的双论域三支决策增量式更新算法,只对变化的数据进行增量式计算,更新时所需的时间远低于非增量式更新算法,因此本文算法具有更高的动态数据更新效率。 针对双论域信息系统的动态更新问题,本文在双论域三支决策模型下提出一种增量式更新算法。分别研究了论域U动态更新和论域V动态更新时,双论域三支决策模型中三个区域的增量式更新,理论分析表明这种更新方式只需对变化的数据进行计算。针对这一更新机制提出了增量式更新算法,实验结果表明增量式算法对于动态双论域信息系统具有更高的更新效率。由于现实中数据的动态性,本文研究成果有助于推动双论域三支决策模型在现实环境下的应用,这将是未来的研究重点之一。2.2 论域V变化时三支决策的动态更新



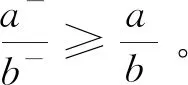
3 双论域下三支决策的更新算法
4 实验分析
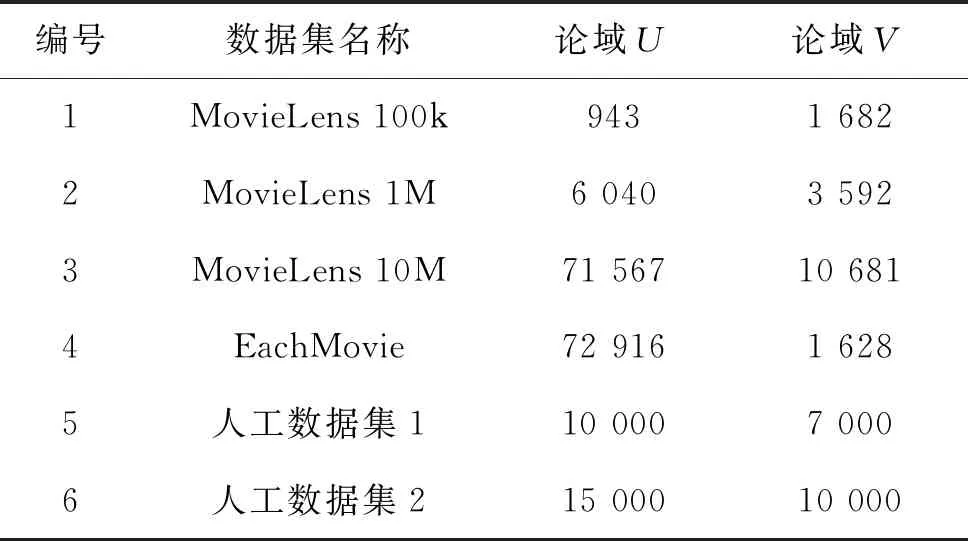
4.1 实验设计与参数设置
4.2 论域U动态更新时增量式与非增量式算法的更新效率比较


4.3 论域V动态更新时增量式与非增量式算法的更新效率比较

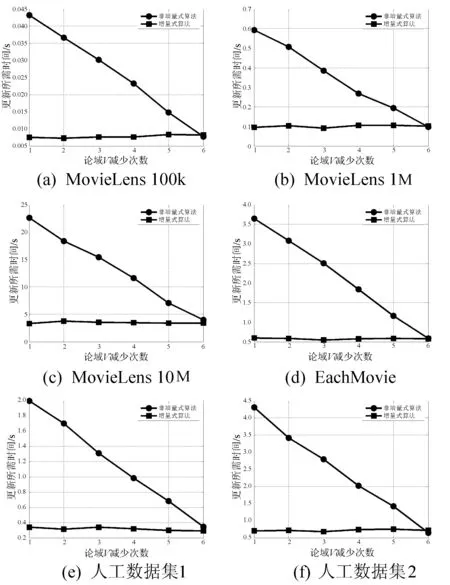
4.4 实验总结
5 结 语
