土方调配问题中土方最优调配方案的LINGO与MATLAB求解
2022-01-07张海涛江汉大学城市地下空间工程系湖北武汉430056
张海涛 (江汉大学城市地下空间工程系,湖北 武汉 430056)
0 引言
土方调配就是指在土方施工中对挖土的利用、堆弃和填土这三者之间的关系进行综合协调处理,以确定填、挖区土方调配的数量和方向,力图使土方总运输量最小或土方施工成本最少。土方调配是土方规划设计的一项重要内容,其求解一般按划分土方调配区、计算各调配区的土方量、计算各挖填方调配区的平均运距、求解土方最优调配方案和绘制土方调配图等步骤进行。
求解土方最优调配方案的理论基础是运筹学中的线性规划模型,即研究在一组线性约束之下,某个线性函数的最小值或最大值问题。在求解线性规划问题的算法中,应用最广泛的是单纯形法,其基本思想是先找到一个基本可行解,检验是否为最优解,否则再找一个使目标函数值有所改进的基本可行解,进行检验。如此反复进行迭代,直至找到最优解,或判断问题无界(即无有限最优值)。
以单纯形法的表格形式即单纯形表形成的“表上作业法”是目前国内土木施工类教材中集中介绍的土方最优调配方案的求解方法。“表上作业法”大致可分为两个步骤进行,一是采用如“最小元素法”确定初步可行解;二是采用如“位势法”或“闭回路法”判别最优解。在工程应用实践中,“表上作业法”需要进行多次闭回路调整,因此其方法存在求解过程繁琐、计算量大、手工计算困难等缺陷。
随着计算机硬件性能的提高和软件技术的发展,求解线性规划问题在目前已经变得十分容易和快捷,本文探讨分别利用LINGO与MATLAB软件解决土方最优调配方案求解问题,从而使工程技术人员能够从复杂的数学计算中解脱出来,使土方最优调配方案问题的求解变得简单、高效。
1 土方最优调配方案的线性规划模型
如表1所示的土方调配平衡表,假设有m个挖方区,用W(i=1,2,…,m)表示,挖方量为a;有n个填方区,用T(j=1,2,…,n)表示,填方量为 b。挖方区W将土运输至填方区T的平均运距为C,X为从 a挖方区调配给 b填方区的土方量。
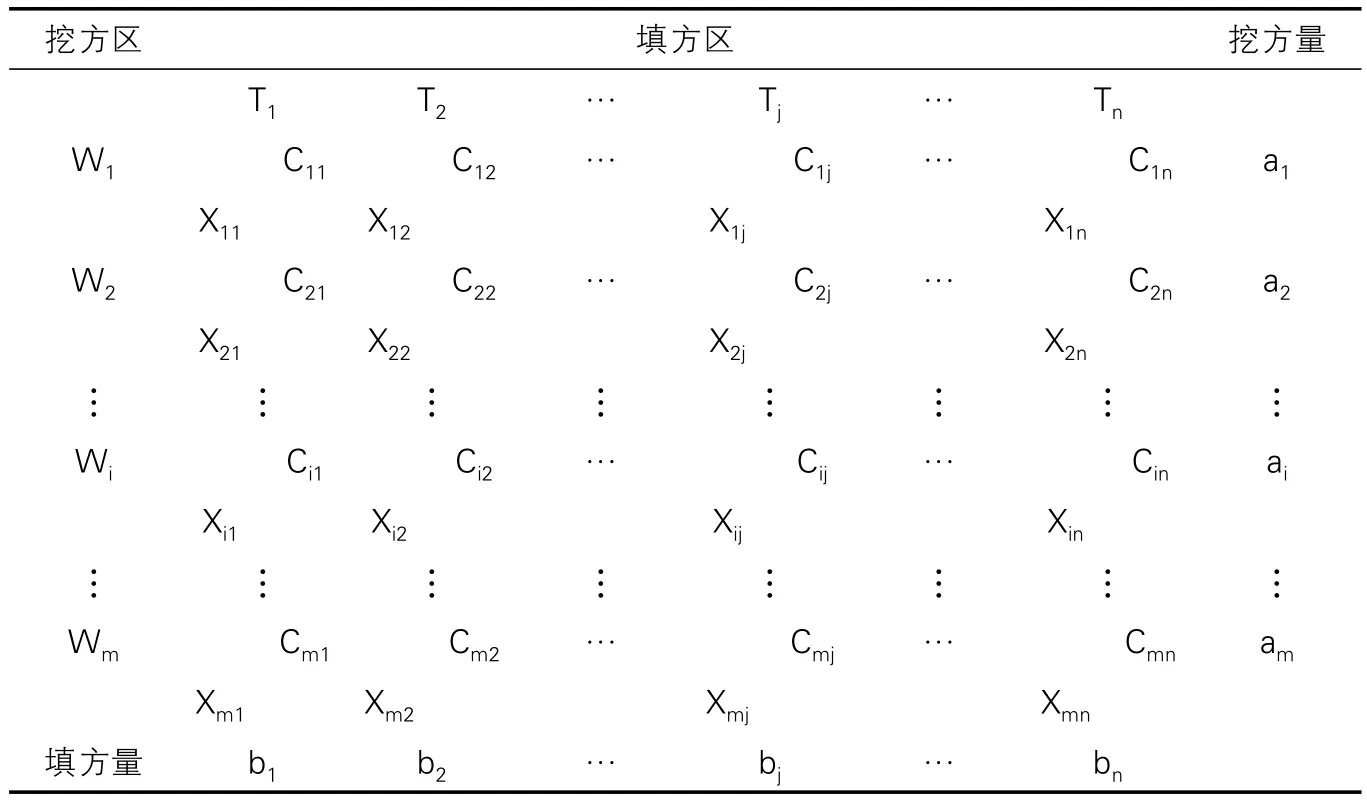
土方调配平衡表 表1
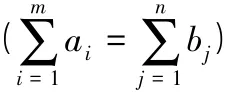

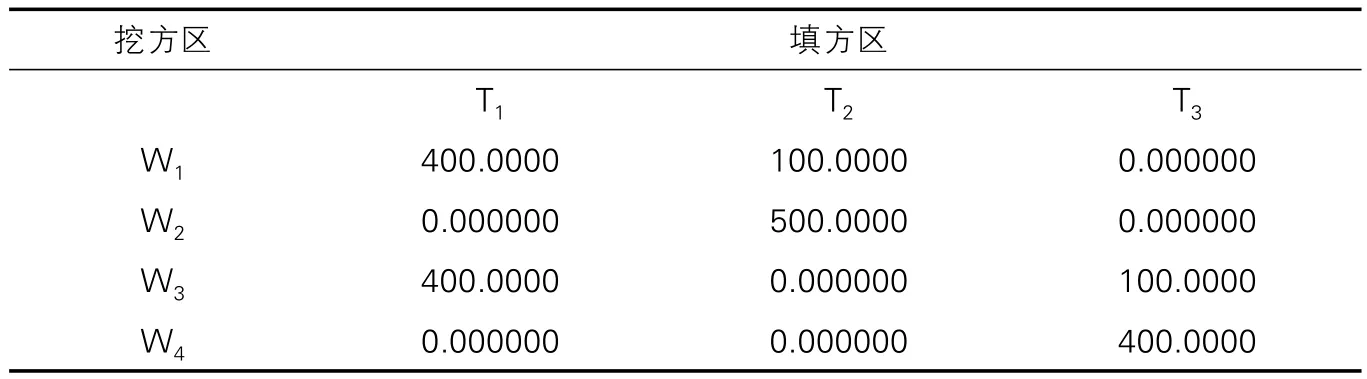
X
的值,使得目标函数(土方总运输量)Z
为最小。2 土方最优调配方案的LINGO与MATLAB求解
以文献[1]中的“表上作业法”案例为例,分别采用LINGO与MATLAB软件求解。案例问题可形成如表2所示的挖、填方量和平均运距表,要求确定土方最优调配方案,即求解出一组各挖方区调配给各填方区的土方量,使得总土方运输量为最小值。

挖、填方量(m3)和平均运距(m)表 表2
2.1 LINGO软件解法
LINGO模型的基本组成包括定义集合、数据段、目标函数和约束条件。依据表2和公式(1)、(2),对案例建立LINGO模型如下:

即目标函数值为94000.00,完整的变量X求解结果总结如表3所示,与文献[1]中的“表上作业法”结果完全一致。
变量XIJ的求解结果表 表3
2.2 MATLAB软件解法
在MATLAB的优化工具箱中,用于求解线性规划问题的函数是linprog,其调用格式[x,fval]=linprog(C,[],[],A,b,lb)可求解如下问题:


其中,C为价值向量,A为等式约束矩阵,b为等式资源向量,lb为决策向量X的下界。[x,fval]表示计算返回结果向量X和最优目标值的计算结果。
结合公式(3)、(4)与表1,这里令:
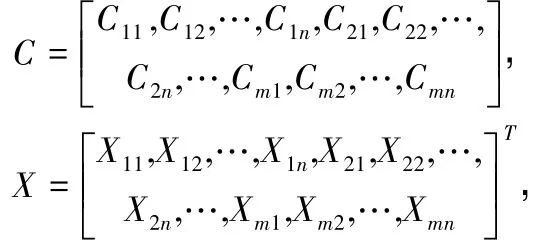

为了方便将模型数据输入到MATLAB软件中,这里按表2数据在Excel电子表格中建立算例的模型数据,如对矩阵A在Excel中的录入格式如图1所示,类似地可录入C、b、lb。

图1 案例矩阵A的Excel数据格式
将建立的Excel文件导入到MATLAB后,在MATLAB的命令窗口中使用命令:
[x,fval]=linprog(C,[],[],A,b,lb)
则计算得到的结果为

3 结语
土木工程中遇到的许多优化问题都可以归结为规划问题,当遇到变量比较多或者约束条件表达式比较复杂的实际工程情况时,试图用手工计算来求解这类问题几乎是难以实现的,编程计算虽然能够代替手工计算快速得出结果,但编程工作量大、较为繁琐且难以被工程技术人员掌握。因此,工程应用中较为可行的方法是通过软件求解。LINGO作为专门用来求解各种规划问题的软件包,具有功能强大、模型输入简练直观、能够以较少的语句描述较大规模的优化模型等特点,其被认为是求解优化模型的最佳选择。MATLAB软件则具有强大的科学计算与可视化功能,并且已经形成了一套涵盖领域广泛的工具箱,如其优化工具箱可以求解线性规划、非线性规划和多目标规划问题,这些特点使其已经成为科研和工程实践必备的工具之一。因此,本文通过对土方最优调配方案的LINGO和MATLAB求解方法的具体描述,旨在帮助工程技术人员能够通过软件快速掌握这类问题的求解方法,进而能够从复杂的数学计算中解脱出来,从而达到提高工程建设效率的目的。
