面向圆形布局位置选择的蚁群劳动分工算法

王英聪，张 领，肖人彬

(1.郑州轻工业大学 电气信息工程学院，河南 郑州 450002；2.华中科技大学 人工智能与自动化学院，湖北 武汉 430074)

0 引言

圆形布局 (circle packing) 问题研究如何将一组半径任意给定的圆形物体互不重叠地放入一个半径尽可能小的圆形容器内，从而使得容器的空间利用率尽可能高[1]。圆形布局问题具有很强的工程应用背景。例如，在电缆行业中，需要将成束的电线聚集成一根电缆，电缆直径越小，需要的绝缘材料越少。在石油产业中，需要在运输管道中布置柴油、汽油等不同类型的输油管，管径越小，成本越低。此外，圆形布局问题在板材加工、设备布局、航空航天、轮船运输等领域也有着广泛的应用[2-4]。与传统的装箱(bin packing)问题主要研究矩形物体和矩形容器不同，圆形布局问题主要研究圆形物体和圆形容器。传统的bin packing问题的求解方法以定序定位法为主，圆形布局问题的求解方法主要分为全装填法和定序定位法，且两者算法框架截然不同。作为一个经典的NP难度问题，圆形布局问题的难点在于如何从一些新的研究视角提出高效的求解方法。

(1)全装填法用容器内的物理格局描述布局解，并通过某些策略在容器内移动圆形物体，其搜索的是整个布局。具体的，全装填法首先将所有圆形物体强行放入容器(不考虑约束条件)，然后不断调整各圆形物体的位置，直到所有圆形物体都满足约束条件，进而找到布局解。全装填法综合考虑了圆形布局问题的连续特征和组合特征，主要包含连续优化和格局变换两个阶段。对连续优化和格局变换的不同设计可形成不同的求解方法，比如文献[4]通过刺激—响应机制执行固定、平移、交换、跳跃等占位动作完成格局变换，通过拟物法进行连续优化。文献[5]采用邻域搜索过程生成新格局，采用拟物方法进行连续优化。文献[6]直接利用人工蜂群算法优化圆形物体的位置，这一过程同时包含格局变换和连续优化。文献[7]采用启发式格局更新策略产生新格局，利用基于自适应步长的梯度法进行连续优化，并结合模拟退火准则接收新格局。文献[8-9]采用基于痛苦度的格局更新策略和基于势能曲面变平法的格局接收准则，在连续优化方面则分别使用了稀疏非线性优化器(Sparse Nonlinear Optimizer，SNOPT)和梯度法。文献[10-11]在格局变换方面采用基于禁忌搜索的邻域结构，在连续优化方面采用拟牛顿法(LBFGS)。全装填法允许圆形物体之间、圆形物体与容器之间存在重叠，其将问题解空间变大，导致其中包含很多不可行的布局解。此外，全装填法中圆形物体的合法位置需要通过连续优化才能得到，计算时间较长。

(2)定序定位法通过放置规则构造布局解，并用圆形物体之间的放置序列描述布局解，其搜索的是放置序列。具体的，定序定位法首先对圆形物体排序，然后按照此顺序，根据放置规则逐个确定圆形物体的位置，当最后一个圆形物体的位置确定时就得到一个布局解。定序定位法主要考虑了布局问题的组合特征，包括确定放置顺序和放置位置两部分。对放置序列的优化和放置规则的设计可形成不同的求解方法，如文献[12]通过遍历法搜索放置顺序，采用最大穴度规则确定放置位置。文献[13]利用树搜索进行定序，基于占角动作进行定位。文献[14-15]分别采用相切定位原则和外围逆时针排列定位原则，并采用蚁群算法搜索放置顺序。文献[16-17]在最大穴度定位规则的基础上采用集束搜索算法搜索放置顺序。文献[18]采用遍历法搜索放置顺序，通过局部最优位置进行定位。文献[19]采用禁忌搜索确定放置顺序，通过分割策略确定放置位置。定序定位法通过放置规则将问题解空间缩小为离散解集，从解空间移除的部分解集中可能包含全局最优解和一些较好的局部最优解。此外，定序定位法中圆形物体的合法位置可利用放置规则直接得到，计算时间很短。

定序定位法中的定序就是对圆形物体排序，这是一个典型的组合优化问题，可以采用很多启发式方法(如蚁群算法、模拟退火算法、遗传算法)进行求解。定序定位法中的定位就是确定圆形物体在容器内的摆放位置，而这样的位置通常不止一个。定位就是从多个可行位置中选择一个恰当的位置放置圆形物体，因而定位可以看作是一个位置选择问题。定位规则的设计既要满足布局的约束条件，又要蕴含目标函数的优化信息，是定序定位法的关键所在。同时，由于定序定位法是在逐步构造布局解，每个阶段位置的选择只能依据当前的布局信息，而当前布局下的最优位置不一定是符合最终布局的最佳位置。因此，如何根据局部信息选择恰当的放置位置是定位规则的设计难点。

蚁群劳动分工是一种典型的群智能行为，经常被认为是蚁群生态成功的首要原因[20]。在蚁群中，族群需要完成觅食、哺育、防御等任务。蚂蚁在无中心控制和缺乏全局信息的情况下，仅通过局部信息的相互作用就能选择出符合族群需求的恰当任务，这种现象叫做劳动分工[21]。在蚁群劳动分工中，蚂蚁对任务的选择还能够随着环境变化进行自适应调整。圆形布局的定位过程可以看作是圆形物体对放置位置的选择，而蚁群劳动分工可以看作是蚂蚁对族群任务的选择。作为选择问题，蚁群劳动分工对圆形布局的定位过程具有启发意义。更重要的是，蚁群劳动分工的特点恰好满足圆形布局对定位规则的设计要求。本文借鉴蚁群劳动分工的任务选择实现圆形布局定位过程中的位置选择，提出一种蚁群劳动分工算法。对于圆形物体的放置顺序，本文采用经典的蚁群优化算法进行求解。最后，对国内外公开的24个代表性算例进行了计算。实验结果表明，本文算法是求解圆形布局问题的一种快速而有效的算法。

1 选择视角下的圆形布局问题

1.1 问题描述

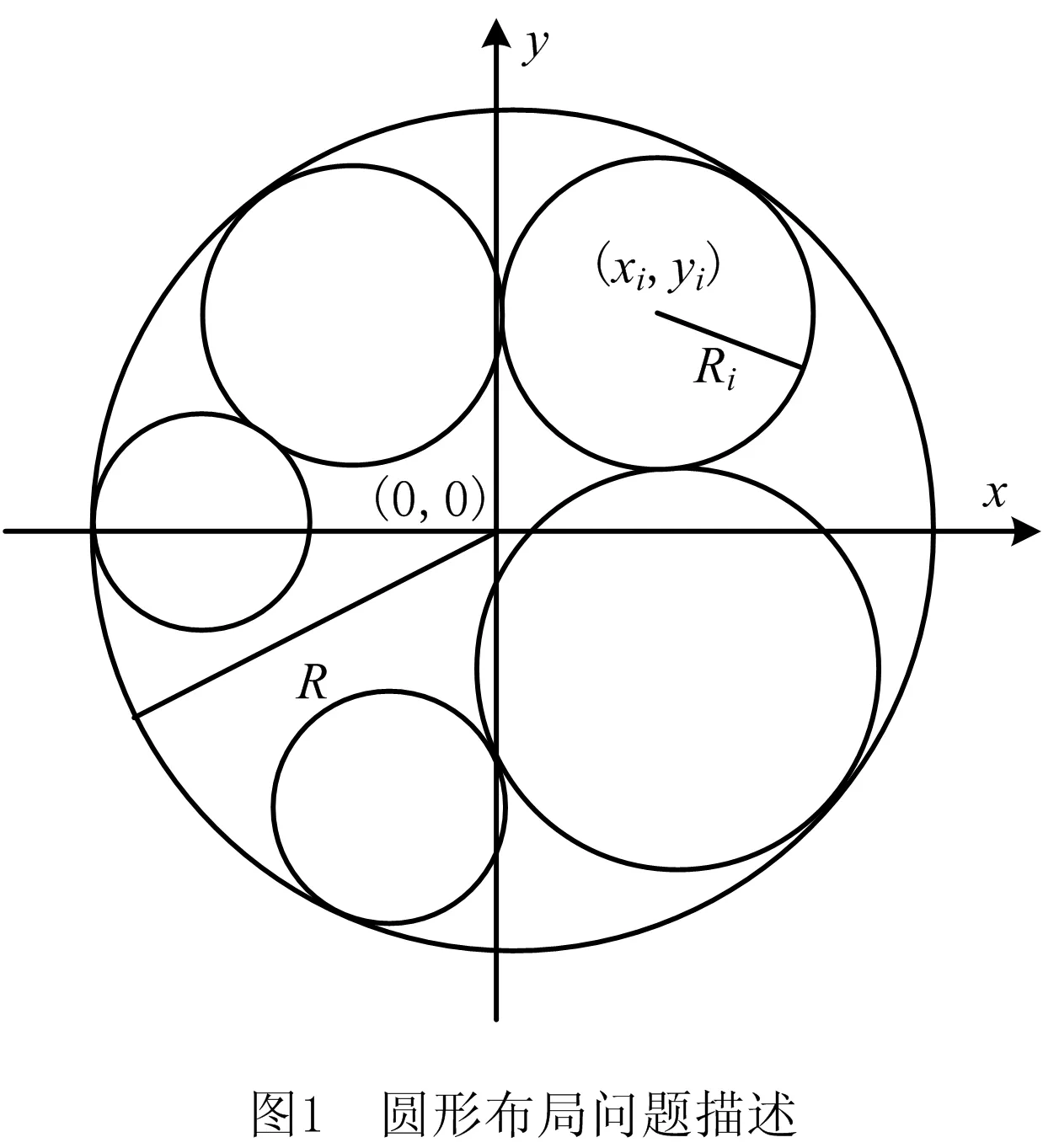
圆形布局问题的一般描述如下：给定n个半径分别为Ri(i=1,2,…,n)的圆形物体，将这些圆形物体互不重叠地放入一个半径R尽可能小的圆形容器内。如图1所示，如果将圆形容器的圆心固定在原点(0, 0)，将第i个圆形物体ci的坐标记为(xi,yi)，则圆形布局问题就转换为寻找一个布局方案X=(x1,y1,x2,y2,…,xn,yn)，使得

(1)

(2)

(3)

其中:目标式(1)是使放置n个圆形物体的圆形容器半径R(即所有圆形物体的外包络圆半径)尽可能小，约束条件式(2)要求任意两个圆形物体之间互不重叠，约束条件式(3)要求每个圆形物体均处于容器范围内。

1.2 选择特性分析

定序定位法在求解圆形布局问题时，首先将圆形物体排序，然后将排序后的圆形物体逐个放入容器中以获得布局解。定序定位法本质上是在确定圆形物体的放置顺序和放置位置，其中放置顺序的确定是一个典型的组合优化问题。对于组合优化问题，目前已有很多较为成熟的求解方法[22]。圆形物体在容器内的放置位置通常不止一个，放置位置的确定就是从多个位置中选择一个恰当的位置。在定序定位方法范畴下，当放置顺序确定以后，圆形布局问题就转化为圆形物体的位置选择问题。由于定序定位法是在逐步构造布局解，每当新的圆形物体放入容器时就会形成新的布局。下面结合格局和可行位置的概念来进一步分析圆形布局问题的选择特性。

定义1格局。假定在圆形容器内已经互不重叠地置入了k(k≥0)个圆形物体，将容器和这k个圆形物体的位置集合称为一个格局Ck。将容器的圆心置入原点，首个圆形物体置入容器边缘并与容器相切形成初始格局C1。当置入容器内的圆形物体个数为n时，称其为合法格局；反之，若置入容器内的圆形物体的个数小于n，且容器外的待置圆形物体不能合法地置入容器时(即不与已布局圆形物体重叠且不超出容器范围)，称其为非法格局。

定义2可行位置。用圆形物体的圆心坐标描述其位置，同时将容器也看作一个已布局的“圆形物体”。对于格局Ck，若将待置圆形物体cj放入容器后，使其与Ck中的任一圆形物体均不重叠且至少与两个圆形物体相切，就将此时圆形物体cj的圆心坐标称为其在格局Ck下的可行位置。

具体的，待置圆形物体cj与已布局圆形物体cp、cq同时相切的位置计算表达式为：

其中：(xj,yj)、(xp,yp)和(xq,yq)分别为圆形物体cj、cp和cq的圆心坐标，Rj、Rp和Rq分别为圆形物体cj、cp和cq的半径。一般情况下，由方程组(4)可计算得到两组坐标。但是将圆形物体cj的圆心置于这些坐标上时，其有可能与容器或容器内除cp、cq外的其他圆形物体相交。如图2a中j2处与容器相交，图2b中j1处与圆形物体ct相交。因此，由方程组(4)计算得到的坐标还需进一步满足约束式(2)和式(3)，才能得到可行位置。

同理，待置圆形物体cj与容器和已布局圆形物体cp同时相切的位置计算表达式为：

其中：(xj,yj)和(xp,yp)分别为圆形物体cj和cp的圆心坐标，Rj和Rp分别为圆形物体cj和cp的半径。一般情况下，由方程组(5)也可计算得到两组坐标。但是将圆形物体cj的圆心置于这些坐标上时，其有可能与容器内除cp外的其他圆形物体相交。如在图2c中，j2处与圆形物体cq相交。因此，由方程组(5)计算得到的坐标还需进一步满足约束式(2)，才能得到可行位置。

结合上述定义，总结圆形物体的位置选择特性如下：

(1)给定一个格局，圆形物体在当前格局下的可行位置通常不止一个，如在图3a中，c4有c41、c42和c43三个可行位置。

(2)将圆形物体放到不同的可行位置上，会形成不同的布局方案。如图3b和图3c中c5的放置位置不同，所形成的布局方案也不同。

(3)不同可行位置的价值或优度一般不同。直观上看，可行位置的优度与格局(这里指将圆形物体放到该位置上所形成的新格局)的紧密程度和剩余空间的完整程度有关。比如，图3d中c61处的格局比c62处的格局更为紧凑，说明c61处的空间利用率更高；对比图3b和图3c，将c5置于容器后，后者的剩余空间比前者更为完整，从而可容纳更多的圆形物体。

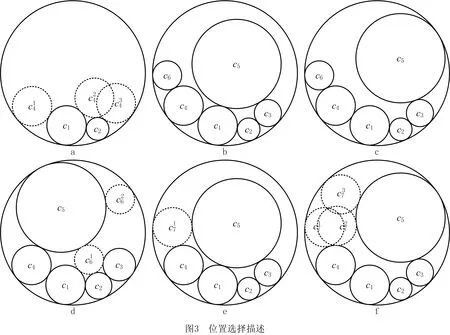
(4)给定不同的格局，圆形物体在容器内的可行位置集合不同。如在图3e和图3f中，c7的位置集合各不相同。当格局中圆形物体数量较少时，待置圆形物体无论半径大小，其在容器内可行位置的数量相差不大；当格局中圆形物体的数量较多时，半径较小的圆形物体在容器内的可行位置数量通常高于半径较大的圆形物体。

2 蚁群定序定位算法

2.1 蚁群优化定序

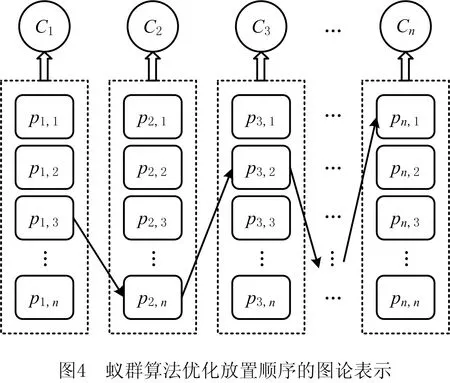
在定序定位法中，确定圆形物体的放置顺序是一个典型的组合优化问题。蚁群算法由于既能利用先验问题知识，又能利用后验解的信息，已被成功用于许多组合优化问题。蚁群算法在解决组合优化问题时，通常将其看作图论中的最优路径问题。本文采用蚁群算法优化放置顺序，对应的图论表示如图4所示。在图4中，pi,j构成了有向图的顶点，表示第i次放置第j个圆形物体，从而形成包含i个圆形物体的格局Ci。由于每个圆形物体均可在布局的各个阶段放入容器中，因而在构造不同阶段的格局时都有n个顶点可供选择。因为已布局的圆形物体不能重复参与布局，理论上当前格局下的每个顶点与后续格局下的顶点之间都有n-1条边。在蚁群算法中，蚂蚁的任务就是构造一条从C1到Cn的最优路径。在具体求解过程中，蚂蚁根据各路径上所积累的信息素及路径的启发信息决定其转移方向。信息素的积累体现的是一种正反馈作用，启发信息则表示对路径的期望程度，可根据某种启发式算法确定[23]。

在蚁群算法的基础上，本文结合圆形布局问题以及定序定位方法的特点，采用伪随机比例规则确定蚂蚁由顶点pk,i转移到顶点pk+1,j的概率：

(6)

(7)

其中：allowedk表示格局Ck下待置圆形物体的集合；xij表示边(i,j)上的信息素；α表示对应的信息启发式因子；yij表示边(i,j)上的启发信息；β表示对应的期望启发式因子；zj表示放置第j个圆形物体的启发信息；γ表示对应的期望启发式因子；q表示区间[0,1]内的一个随机数；q0表示决策点，0≤q0≤1。

(8)

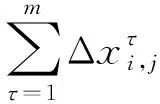
蚁群算法在解决经典组合优化问题旅行商问题(Traveling Salesman Problem，TSP)时，边(i,j)上的启发信息yij表示由城市i转移到城市j的期望程度。一般而言，城市之间的距离越短，转移的期望程度越高，yij通常取城市之间距离的倒数。定序定位法在解决圆形布局问题时将圆形物体逐个置入容器，放置时还要考虑格局的紧凑性。一般而言，放置顺序相邻的物体之间的放置位置也相邻。本文用最优布局中各圆形物体之间的距离描述启发信息，即

yi,j=1/(di,j+r)，

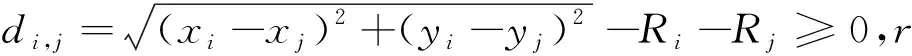
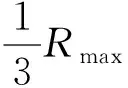
2.2 蚁群劳动分工定位

2.2.1 劳动分工与定位过程之间的映射

在蚁群等社会性昆虫中，族群需要完成哺育、觅食、筑巢、防御等任务。蚁群劳动分工表现为不同的蚂蚁执行不同的任务，且执行各项任务的蚂蚁的比率在内部繁衍生息和外部侵略挑战的作用下可以动态变化，而该比率下蚂蚁的分工恰好满足族群对各项任务的需求。更重要的是，蚁群中的蚂蚁既不具备任何关于族群需求的全局信息，也不存在一个领导者指挥蚂蚁的行为，蚂蚁仅根据局部信息就能选择出符合族群需求的恰当任务。蚁群劳动分工本质上是一种任务分配，也可以看作是蚂蚁对任务的选择。

圆形布局问题的定位过程就是确定圆形物体在容器内的放置位置，而这样的位置通常不止一个，定位过程则要求从多个可行位置中选择一个恰当的位置放置圆形物体。因此，定位过程可以看作是圆形物体的位置选择问题。定序定位法将圆形物体逐个置入容器，在每个阶段的定位过程中，圆形物体的位置选择只能依据当前格局的局部信息，而当前格局下的最优位置不一定是符合整体布局的最佳位置。因此，如何根据局部信息选择恰当的放置位置是定位过程的难点所在。

蚁群劳动分工可以看作是蚂蚁对任务的选择，圆形布局问题的定位过程可以看作是圆形物体对可行位置的选择。将圆形物体看作蚂蚁，可行位置看作任务，则任务选择可为位置选择提供参考。据此，本文提出一种蚁群劳动分工定位算法。表1从选择的视角进一步对比分析了蚁群劳动分工和圆形布局的定位过程，二者都属于离散选择范畴，这为本文方法的可行性提供了依据。同时，蚁群劳动分工仅利用局部信息就能选择出恰当任务的特点，恰好符合圆形布局对定位过程中位置选择的要求，这进一步增强了本文方法的可行性。

表1 蚁群劳动分工和圆形布局定位过程之间的比较

2.2.2 劳动分工中的刺激-响应原理

蚁群劳动分工中的刺激-响应原理可简要描述如下：族群中每个任务都对应一个刺激，刺激的强度描述了任务的紧急程度。蚂蚁对于每个任务都存在一个阈值，阈值的大小反映了蚂蚁响应不同任务的实际差别。当任务的刺激强度超过蚂蚁的响应阈值时，蚂蚁选择任务的概率高；反之，蚂蚁选择任务的概率低。BONABEAU[24]和THERAULAZ[25]等给出了刺激—响应原理的一种量化形式：假设某个任务的刺激为S，蚂蚁对应的阈值为θ，则蚂蚁选择该任务的概率为P=S2/(S2+θ2)。刺激—响应原理通过环境和个体的自组织交互实现了蚂蚁对任务的选择，并被成功用于一些任务选择问题[26-28]。

2.2.3 劳动分工定位算法

将圆形物体看作蚂蚁，可行位置看作任务，分别为可行位置和圆形物体设置恰当的刺激和阈值，则利用蚁群劳动分工中的刺激-响应原理就可实现圆形物体对可行位置的选择。对刺激和阈值的设计需要结合圆形布局问题定位过程的特点，这里主要考虑两个原则：①增大对已布局空间的利用;②减小对未布局空间的破坏。

(1) 刺激

圆形布局问题的目标是最大化容器的空间利用率。由于定序定位法是在逐步构造布局解，在每一阶段一般都会要求已布局的空间尽量紧凑，这样才能逐渐提高容器的空间利用率。将待置圆形物体放到给定格局下某个可行位置上以后，若该物体与其他已放好的圆形物体之间的位置紧密，则说明新格局下已布局空间的利用率高。圆形物体之间的位置关系可由彼此的距离来度量，距离越短，位置越紧密。计算待置圆形物体在可行位置上与容器内其他圆形物体(排除计算可行位置的圆形物体)之间的距离，将这些距离由小到大排序后进行加权求和，以此定义新格局的局部密度，如式(9)所示。

(9)

在定位过程中，将待置圆形物体放到某个可行位置上后，若所形成格局的局部密度越大，说明其对已布局空间的浪费越小，优先选择该位置的机会一般也越大。在刺激—响应原理中，任务的刺激越大，个体选择任务的概率越大。因此，可将局部密度看作刺激，假设二者具有正比关系：S=ω×Den。

(2)阈值

定序定位法在逐步构造布局解的过程中，将容器空间分为已布局空间和未布局空间两部分。为提高容器的空间利用率，除了要求已布局空间尽量紧凑以外，一般还要求未布局空间连续完整，这样才能放置更多的圆形物体。直观上看，将圆形物体放到容器中心或者靠近中心的位置上时，其对容器空间连续性的破坏比较大。这与穴度算法[29]中基于“金角银边草肚皮”的放置思路相似，即容器腹地位置的价值较低。计算待置圆形物体在可行位置上与容器中心的距离，以此定义对应位置的容器中心度，如式(10)所示：

(10)

在定位过程中，将待置圆形物体放到某个可行位置上后，若其对应的容器中心度小，说明其对容器剩余空间的破坏较小，优先选择该位置的机会一般也较大。在刺激—响应原理中，个体的阈值越小，个体选择任务的概率越大。因此，可将中心度看作阈值，假设二者具有正比关系：θ=υ×Cen。

(3)选择概率

假设待置圆形物体在当前格局下共有t个可行位置，与第i个可行位置对应的刺激和阈值分别为Si和θi，则根据刺激—响应原理，待置圆形物体选择第i个可行位置的概率为：

(11)

(4)定位过程

当圆形物体的放置顺序确定时，劳动分工定位算法将按照该顺序逐个放置圆形物体，主要包括以下4个步骤：①在当前格局下，计算出待置圆形物体在容器内的可行位置；②将待置圆形物体“试放”到每个可行位置上，通过分别计算待置圆形物体与已布局圆形物体和容器的位置关系，得到与可行位置对应的刺激和阈值；③待置圆形物体根据式(11)选择可行位置进行放置；④更新当前格局，得到新的格局。重复上述过程，直到最后一个圆形物体置入容器内，或者没有可行位置放置待置圆形物体为止。

(5) 参数分析

定位过程即为圆形物体选择恰当的位置，一般会优先考虑使已布局空间紧凑和未布局空间连续的位置。上述定义的局部密度和容器中心度可以分别描述已布局空间的紧凑性和未布局空间的连续性，将二者的比值作为可行位置的优度。劳动分工定位算法中有刺激比例系数ω和阈值比例系数υ两个参数。化简式(11)可知，二者以比例(ω/υ)的形式影响圆形物体对可行位置的选择。当(ω/υ)过大时，选择优度小的可行位置的概率会显著增大，而选择优度大的可行位置的概率则变化不明显，此时圆形物体将以近似随机的方式选择可行位置；当(ω/υ)过小时，选择优度大的可行位置的概率会减小，而选择优度小的可行位置的概率则会趋于零，此时圆形物体将近似以贪婪的方式选择优度大的可行位置；对(ω/υ)取值的设置，应使得选择优度大的可行位置的概率和选择优度小的可行位置的概率保持在接近的量级，从而避免随机选择或者贪婪选择的出现。

(6)计算复杂度

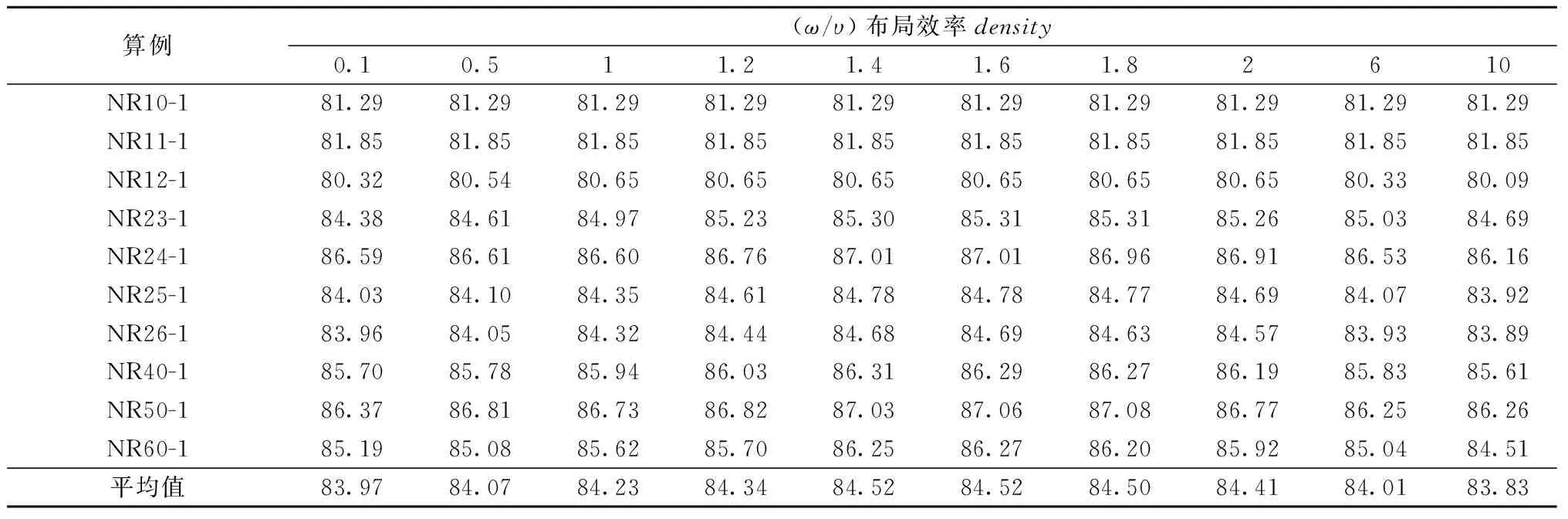
表 2 不同参数(ω/υ)下的平均效率 %

2.3 完整的定序定位算法

结合上述蚁群优化定序和蚁群劳动分工定位，图5给出了完整的定序定位算法流程图。

3 实验结果与比较

本文算法通过Java实现，并在CPU主频为2.40 GHz、内存为4 GB的PC机上进行实验。选取两组具有代表性的国际公开算例作为测试集，其中第1个测试集来自文献[12]，第2个测试集来自文献[30]。

3.1 参数设置

本文算法包括蚁群优化定序和蚁群劳动分工定位两部分，其中定位算法的设计是本文的重点。蚁群优化定序中信息素、启发式因子等参数的设置已在2.1节给出，本节主要讨论蚁群劳动分工定位中刺激—阈值比例系数(ω/υ)的取值。具体的，从第一个测试集中选10个算例来研究(ω/υ)对布局结果的影响，并用占空比density(即置入容器内所有圆形物体面积之和与容器面积的比值)来度量布局效率。

在(ω/υ)的不同取值下，每个算例独立运行5次，表2给出了5次实验的平均布局效率。从表2可以看出，(ω/υ)∈[1.4,2]时布局效率较高，这与第2.2.3节的参数分析结论一致。(ω/υ)以平方的形式影响圆形物体对可行位置的选择，取值过小时近似为贪婪选择，取值过大时近似为随机选择。因此，本文实验中将(ω/υ)的值设为1.6。

3.2 计算结果

圆形布局问题的求解方法可以分为全装填法和定序定位法两大类。对比已有文献发现，大部分方法属于全装填法，而对定序定位法的研究较少。本文算法属于定序定位法，为了验证该算法的有效性，分别将其与最新的全装填法和经典的定序定位法进行比较。对于测试集中的每个算例，独立运行本文算法10次，记录其中的最小容器半径和平均运行时间。

表3给出了本文算法与全装填法——迭代禁忌变邻域下降算法(Iterated Tabu Search and Variable Neighborhood Descent, ITS-VND)[11]和空间分

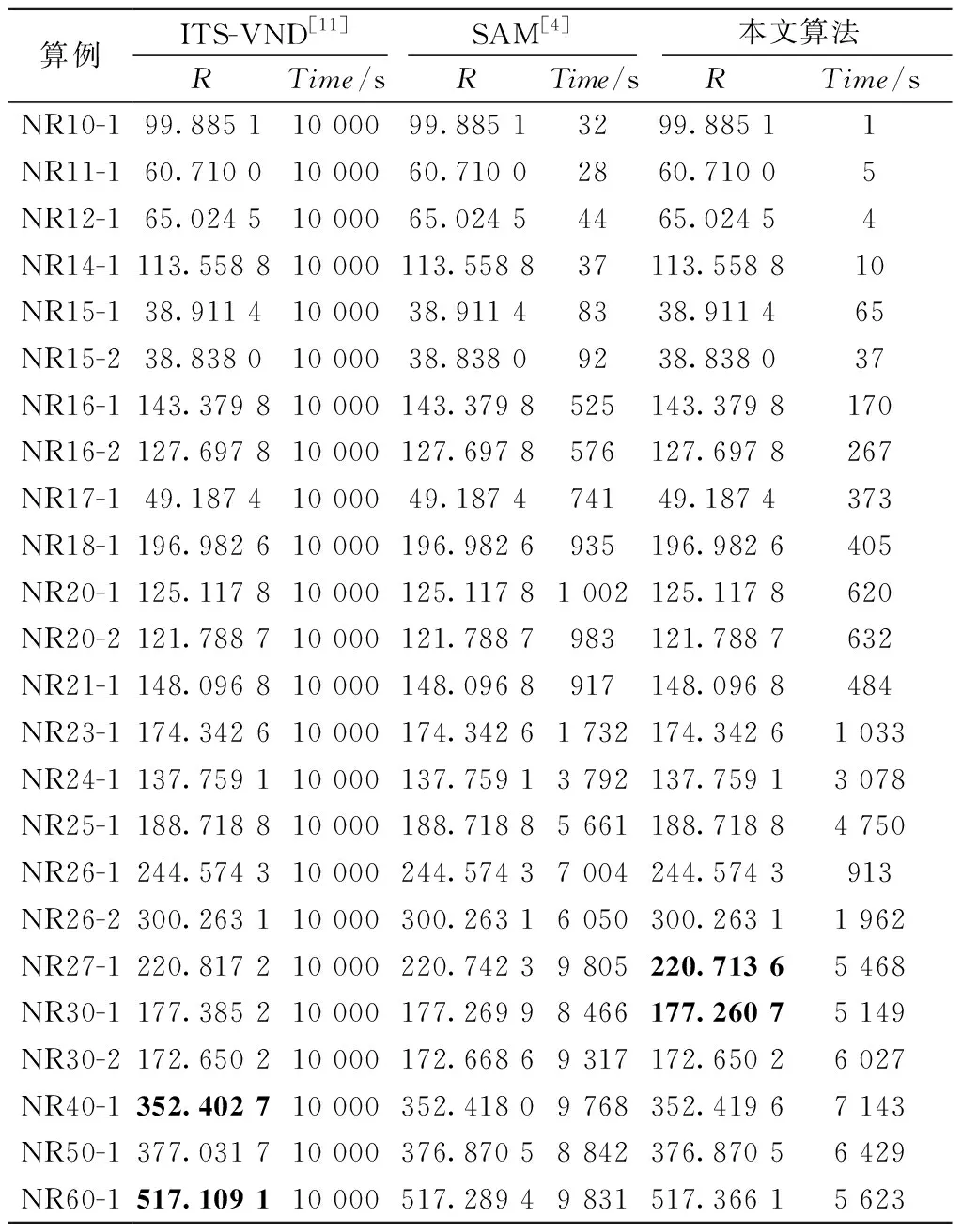
表3 本文算法与全装填方法的结果比较

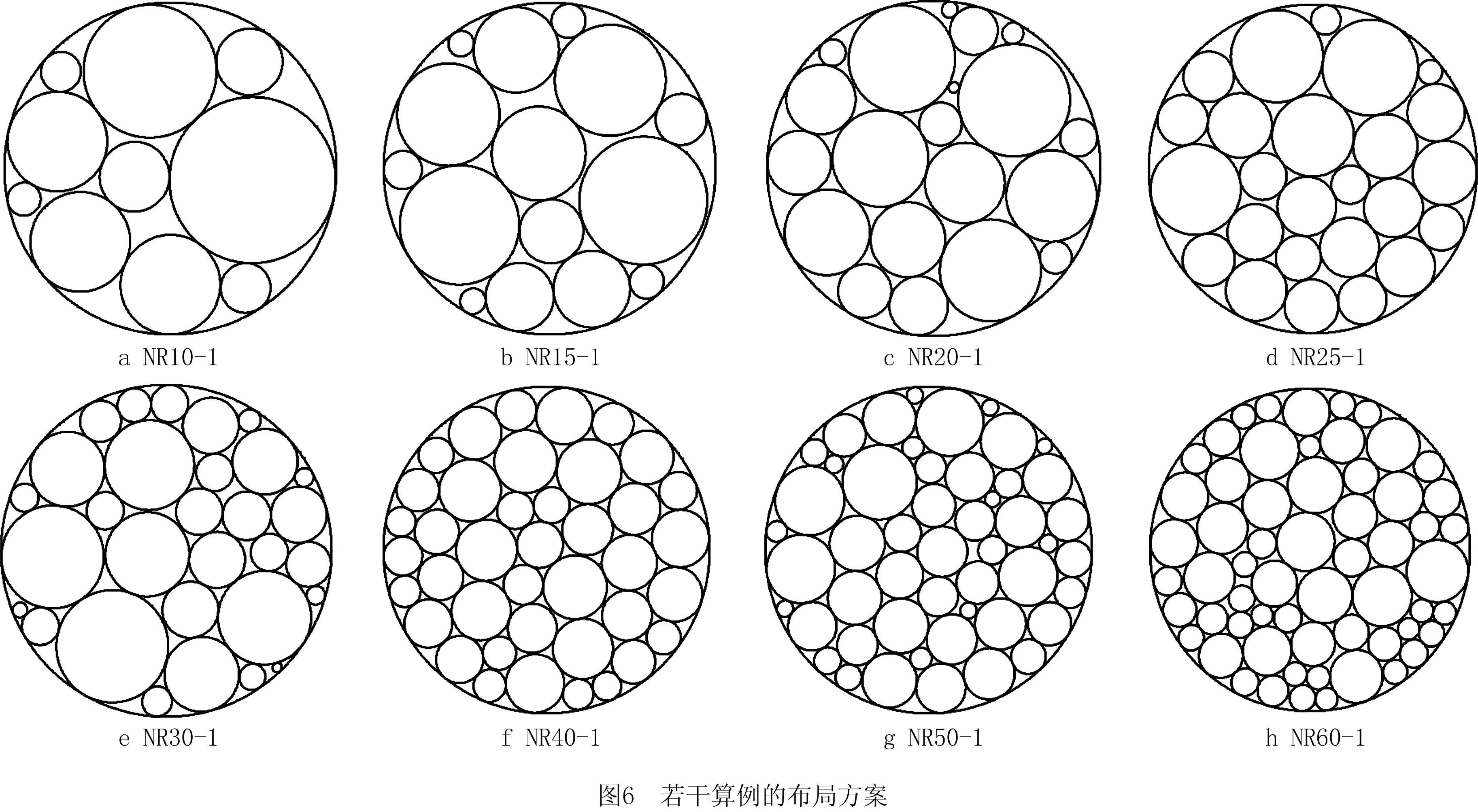
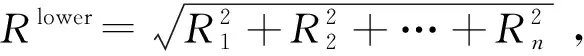
表4给出了本文算法与其他定序定位法——启发式算法1(Algorithm 1.0,A1.0)[12]、启发式算法1.5(Algorithm 1.5,A1.5)[12]、集束搜索法(Beam Search, BS)[16]、自适应集束搜索法(Adaptive Beam Search, ABS)[17]在第一个测试集上的结果比较，每个算例的最小容器半径用粗体表示。由表4可以看出，本文算法所得结果在算例NR11-1上与A1.5持平，在算例NR10-1和NR11-1上与BS持平，其余结果均优于A1.0、A1.5和BS。与ABS相比，本文算法在4个算例上取得了相同的结果，在剩余17个算例上取得了更好的结果。本文算法在这17个算例上的平均改进幅度为0.29%，其中在算例NR40-1上的改进幅度最大，在算例NR12-1上的改进幅度最小，分别为(355.658 7-352.419 6)/355.658 7=0.91%和(65.033 8-65.024 5)/65.033 8=0.01%。另外，本文算法的计算时间也比ABS短。

表4 本文算法与定序定位方法的结果比较

上述定序定位法提出时间过早，为进一步验证本文算法在进行定序定位求解时的有效性，选择与文献[30]中的定序定位算法(Sequential Positioning Algorithm，SPA)继续作对比实验。由于SPA是针对圆形物体和矩形容器的一种定序定位算法，对比时需要将圆形容器扩展为矩形容器。圆形容器对应的目标是最小化容器半径，矩形容器对应的目标是宽度固定的情况下最小化容器的长度。主要扩展思路如下：对于待置圆形物体ci，将其与已布局圆形物体和矩形底边同时相切的位置，与已布局圆形物体和矩形长边同时相切的位置，以及与矩形底边和长边同时相切的位置，都纳入潜在可行位置中，并通过不干涉约束删除其中的不可行位置。矩形容器内与可行位置对应的阈值，用待置圆形物体在可行位置上到容器底边中心线的距离来度量。表5给出了本文算法与SPA在第2个测试集上的结果比较，每个算例的最小容器长度用粗体表示。从表5可以看出，在30个测试算例中，本文算法在20个算例上取得的结果优于SPA，在8个算例上取得的结果与SPA持平，在2个算例上取得的结果不如SPA。SPA在每个算例上的平均计算时间为35.62 s，本文算法在每个算例上的平均计算时间为75.28 s。

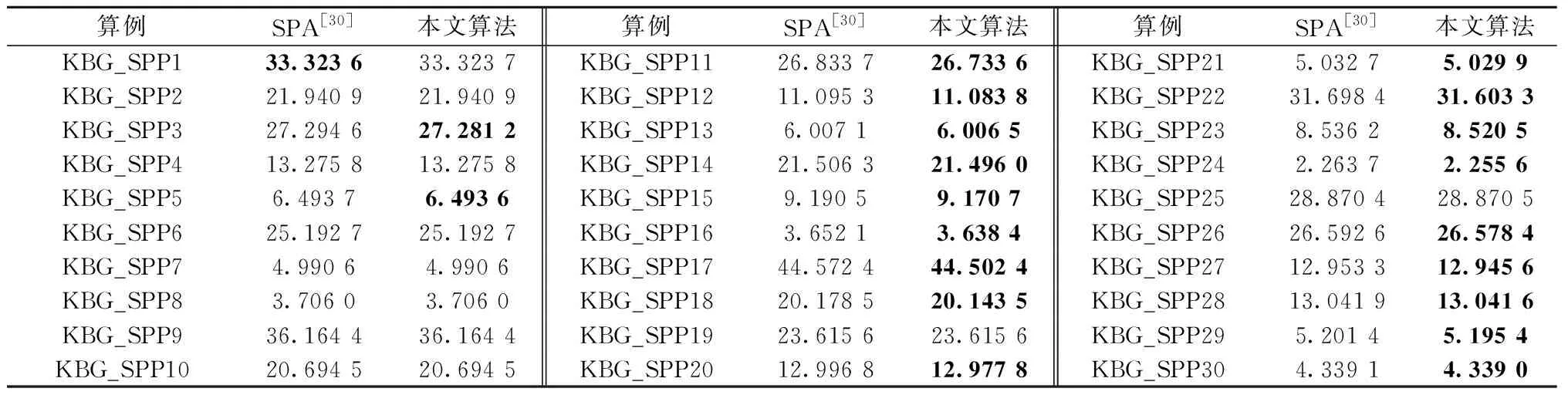
表5 本文算法与SPA的结果比较

3.3 分析讨论

本文提出的蚁群劳动分工定位算法将圆形布局问题的定位过程看成一个位置选择问题，并通过刺激—响应的方式为圆形物体选择可行位置。3.2节通过与其他算法的横向对比，检验了本文算法的性能，这里进一步分析算法内部刺激—响应选择方式的特性。具体的，在本文算法框架下，分别设计随机选择方式和贪婪选择方式进行对比。在随机选择方式中，圆形物体等概率选择可行位置。在贪婪选择方式中，圆形物体始终选择优度最高的可行位置。

选取第一个测试集中的24个算例进行对比实验，刺激—响应选择(Stimulus-Response Selection, SRS)、随机选择(Random Selection, RS)和贪婪选择(Greedy Selection, GS)在每个算例上都独立运行10次。表6从最优值(Best)、平均值(Average)和标准差(Standard Deviation, SD)3个方面给出了3种选择方式的实验结果，每个算例的最好结果用粗体表示。

从表6可以看出：

(1)在最优值方面，与RS相比，SRS在所有算例上的平均改进幅度为4.18%，其中在算例NR10-1上的改进幅度最小为0.11%，在算例NR40-1上的改进幅度最大为8.58%。与GS相比，SRS在所有算例上的平均改进幅度为0.75%，其中在算例NR16-1上的改进幅度最小为0.02%，在算例NR40-1上的改进幅度最大为3.94%。

(2)在平均值方面，与RS相比，SRS在所有算例上的平均改进幅度为7.73%，其中在算例NR12-1上的改进幅度最小为1.36%，在算例NR17-1上的改进幅度最大为18.70%。与GS相比，SRS在所有算例上的平均改进幅度为0.62%，其中在算例NR11-1上的改进幅度最小为0.02%，在算例NR40-1上的改进幅度最大为3.01%。

(3)在标准差方面，SRS在所有算例上的平均值为1.04，RS在所有算例上的平均值为6.81，GS在所有算例上的平均值为0.82，说明RS的稳定性最差，SRS和GS的稳定性相当。

表6 三种选择方式的比较

文献[31]将算法的收敛性定义为其在优质解附近逼近最优解的能力，将算法的多样性定义为其通过探索未搜索区域逼近最优解的能力。在随机选择方式下，圆形物体无差别地选择放置位置，具有很大的盲目性。再结合布局问题的组合特征，导致其在较优解附近(或未探索区域)逼近最优解的能力较差。在贪婪选择方式下，圆形物体始终选择优度最高的放置位置。由于是在逐步构造布局解，这样的选择方式很容易使搜索陷入局部最优。再结合布局问题局部最优解多的特点，导致其搜索区域小且容易过早停滞在次优解处。刺激—响应选择方式在综合考虑已布空间紧密度和未布空间完整度的情况下，通过刺激和阈值的相互作用确定圆形物体的放置位置，该选择过程继承了蚁群劳动分工的任务选择柔性，表6的对比结果进一步表明了其有效性。从概率的角度来看，随机方式下所有放置位置被选中的概率相同；贪婪方式以概率1选择当前最优的放置位置；刺激—响应方式下各放置位置被选中的概率与其优度有关；随机方式和贪婪方式是刺激—响应方式的两种极端情况。

4 结束语

定序定位法求解圆形布局问题时，按照放置顺序(定序)将圆形物体逐个置入容器中适当的位置(定位)。本文从“定位可以看成是一个位置选择问题”的角度出发，即从多个可行位置中选择一个恰当的位置放置圆形物体，提出一种蚁群劳动分工算法。该算法的核心思路是借鉴蚁群劳动分工的任务选择实现定位过程的位置选择，并将定位过程对已布局空间的紧密性要求映射成蚁群劳动分工中的刺激，将定位过程对未布局空间的完整性要求映射成蚁群劳动分工中的阈值。蚁群劳动分工的任务选择柔性使得位置选择具有一定的灵活性，从而在一定程度上维持了搜索格局的多样性。对两组国际公开测试集的计算结果表明，本文算法是求解圆形布局问题的一种快速而有效的算法。

在今后的工作中，拟将本文算法扩展应用于三角形和不规则形状等物体的布局设计。此外，布局问题与经典的背包问题、下料问题和装载问题非常类似，相关成果还可进一步推广到这类问题的求解中。