面向高效低碳的切削参数与柔性作业车间调度集成建模与优化
2022-01-06詹欣隆张超勇孟磊磊连裕翔薛燕社
詹欣隆,张超勇+,孟磊磊,连裕翔,薛燕社
(1.华中科技大学 数字制造装备与技术国家重点实验室,湖北 武汉 430074;2.聊城大学 计算机学院,山东 聊城 252059)
0 引言
当前社会发展正面临不可再生资源枯竭和生态环境恶化的严峻挑战,能源的大量消耗引发了各种环境问题,其中温室气体排放量增加导致的全球变暖问题尤为严峻。制造业是国家的支柱产业,在制造过程中能源被大量消耗,同时产生大量的污染物和二氧化碳,如何解决制造过程产生的碳排放已成为一个热门的研究课题。传统制造业工艺参数优化与车间调度优化通常独立进行,将切削参数与调度方案之间协同优化,能更好地解决车间高效低碳优化问题。
近些年来,低碳制造开始得到一些学者的重视。MOUZON等[1]提出一种以减少能耗和总拖期为目标的单机调度模型,该模型采用开关机策略,在机器闲置时将机器关闭,并在新工件出现之前将其打开以减少能耗。FANG等[2-3]提出一些关于流水车间调度问题的新数学模型,该模型考虑了峰值功率负荷,能耗以及相关的碳足迹等。
在加工过程中,合理的切削参数选择和车间调度方案对于降低车间碳排放和优化经济性指标有重要意义。RAJEMI等[4]建立了机械加工过程总能耗模型,提出一种通过提高刀具使用寿命来获得最小能源足迹的切削参数优化方法。DING等[5]建立了磨削加工参数碳排放相关优化模型,对磨削过程中机床能耗、润滑油消耗、磨削液消耗、磨屑处理和砂轮损耗产生的碳排放进行优化。YUSUF等[6]建立了车削过程中表面质量和碳排放与切削参数之间的数学关系,并采用目标规划方法对其进行优化求解。DAI等[7]提出一种灵活的流水车间调度的节能模型,并使用一种遗传—模拟退火算法来解决该问题。LUO等[8]提出一种新的蚁群优化元启发式算法,用于优化混合流水车间调度问题中的生产效率和电力成本。LIU等[9]针对经典作业车间调度问题,以总能耗和总加权拖期为目标,提出一种多目标调度算法。YIN等[10]针对柔性作业车间调度提出一种新的混合整数规划模型,并提出一种基于单纯形点阵设计的多目标遗传算法对该模型进行求解。目前,低碳研究大部分都是将车间调度和切削参数优化问题独立进行,忽视了切削参数与车间调度之间复杂的影响机理,限制了优化空间。因此,有一些学者意识到这个问题后,开始将车间调度问题和切削参数优化结合起来。LIN等[11-12]以最大完工时间、机床能耗和刀具损耗引起的碳排放为优化目标,提出了切削参数与阻塞流水车间调度集成优化模型,并对其进行求解。FANG 等[2]在进行流水车间调度优化时,考虑了不同切削参数对于面向低碳的优化结果影响。然而,目前将车间调度与切削参数结合起来的研究针对的都是较为经典的调度车间,而像柔性作业车间调度(Flexible Job shop Scheduling Problem,FJSP)这种更贴合实际生产的调度车间,因其与切削参数集成的优化问题更加复杂,尚未有文献对其进行研究。
针对切削参数与柔性作业车间调度集成优化问题,本文首次构建了切削参数与柔性作业车间调度问题集成数学模型,提出了一种改进的离散化引力搜索算法求解该问题。在柔性作业车间和切削参数多重条件约束下,以制造过程碳排放和最大完工时间为优化目标,建立切削参数与柔性作业车间调度集成优化多目标优化模型,提出了工件序列—机器序列—切削参数模式三层编码。在求解切削参数模式对应的切削参数组合时,建立了单道工序的加工过程碳排放和切削加工时间多目标优化模型,使用了笔者[13]提出的改进引力搜索算法对其进行求解,得到单道加工工序的Pareto解集供切削参数模式选择。在所提算法中,设计了一种新的竞选机制,并采用多点交叉和变邻域搜索实现全局搜索和局部搜索有机结合。最后,通过实验验证了所提算法的优越性与集成模型的有效性。
1 切削参数和柔性作业车间调度集成优化模型
切削参数和柔性作业车间调度集成优化问题(Integrated optimization of Cutting Parameters and Flexible Job shop Scheduling Problem,ICPFJSP)可描述如下:给定n个独立的加工工件J={J1,J2,…,Ji,…,Jn},在m台机器M={M1,M2,…,Mm}上进行加工,每个工件Ji包含ni道工序{Oi,1,Oi,2,…,Oi,j,…,Oi,ni}。工件Ji的第j道工序Oi,j在可选机器集合Mij(Mij⊂M)中选择任意一台机器进行加工,且在任一可选机器上的切削速度和进给量不固定。同一工序在同一机器上以不同的切削速度和进给量组合加工时,实际切削时间和切削时产生的碳排放是不同的。该集成优化问题的目标是确定各机床所有加工工序的最优加工次序,同时为每道工序分配最优的加工机器、切削速度和进给量,以优化最大完工时间和制造过程碳排放目标。
1.1 制造过程加工车间碳排放量化模型
加工车间碳排放TCE主要由机床碳排放和车间公共碳排放两部分组成。机床碳排放主要包括切削加工碳排放和机床空载碳排放。
(1)切削加工碳排放
切削加工碳排放PCE指的是机床处于切削加工状态所产生的碳排放:
(1)
式中:Cpijk是工件i的工序j在可选加工机器k上切削加工过程中产生的碳排放。
Cp=Ce+Ct+Cc。
(2)
式中:Cp为工序在加工机器上加工产生的碳排放,Ce为电能消耗产生的碳排放,Ct为刀具使用时产生的碳排放,Cc为切削液使用产生的碳排放。
Ce=FeEe。
(3)
式中:Fe为电能碳排放因子;Ee为加工过程中电能消耗,Ee=PcT,Pc为切削功率,T为切削时间。
(4)
结合上式得
(5)
(6)
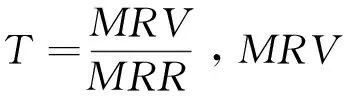
(7)
式中:Tc为切削液更换周期;Cw和Co分别为废弃切削液处理产生的碳排放量和切削液中的矿物油制备所产生的碳排放量,
Co=Fo(Cc+Ac),
(8)
Cw=Fw[(Cc+Ac)/δ]。
(9)
其中:Fo为纯矿物油碳排放因子,Fw为废物切削液处理碳排放因子,Cc为初始切削液用量,Ac为附加切削液用量,δ为切削液浓度。
结合式(7)~式(9)得:
(10)
联合式(5)、式(6)和式(10)得:
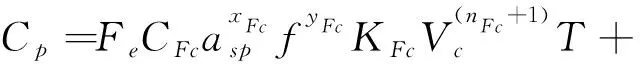
(11)
(2)机床空载碳排放
机床空载碳排放WCE指的是机床在空载闲置时产生的碳排放:
(12)
式中:Pu0m为最低空载功率,TIdelm为空载时间。
(3)车间公共碳排放
车间公共碳排放CCE指的是维持车间公共设施正常工作产生的碳排放,
CCE=P0Cmax。
(13)
式中:P0为公共功率,Cmax为最大完工时间。
(4)制造过程车间总碳排放
制造过程车间总碳排放TCE为总切削碳排放、机床空载碳排放和车间公共碳排放之和,

(14)
1.2 集成优化模型
根据以上对加工车间碳排放量化的目标函数,以及柔性作业车间调度问题考虑最多的最大完工时间最小目标函数,定义集成模型多目标函数如下:

(15)
minCmax=max {Ci|i=1,2,…,n}。
(16)
式(15)和式(16)定义了本文的优化目标,即同时优化车间总碳排放和最大加工时间最小化(makespan)。在集成优化模型中,每道工序对应的加工时间是将切削参数优化模型和柔性作业车间调度模型结合起来的桥梁。通过切削参数优化确定加工每道工序对应的f和Vc,从而确定每道工序的加工时间Ti,j,k。
FJSP问题相关符号定义如表1所示:

表1 符号定义
FJSP决策变量如下:
集成问题约束如下:
fmin≤f≤fmax;
(17)
Vcmin≤Vc≤Vcmax;
(18)
(19)
(20)
(21)
(22)
∀i∈J,∀j∈{1,2,…,ni-1},CEi,j≤SEi,j+1;
(23)
∀g,i∈J,∀h∈Jg,∀j∈Ji,∀k∈M,CEg,h=SEi,j+L(1-yghijk);
(24)
∀k∈M,∀i∈J,∀j∈Ji,Sk≤SEi,j+L(1-xi,j,k);
(25)
∀k∈M,∀i∈J,∀j∈Ji,CEi,j·xi,j,k≤Fk;
(26)
(27)
∀k∈M,Sk≥0。
(28)
若PM[Oi,j]=-1,PJ[Oi,j]=-1,令CEPM[Oi,j]=0,CEPJ[Oi,j]=0则有

(29)
若SM[Oi,j]=-1,SJ[Oi,j]=-1,令SLSM[Oi,j]=Cmax,SLSJ[Oi,j]=Cmax则有
∀i∈J,∀j∈Ji,CLi,j=min(SLSM[Oi,j],SLSJ[Oi,j])。
(30)
其中:式(17)表示每道工序各自对应的进给量约束;式(18)表示每道工序各自对应的切削速度约束;式(19)表示每道工序各自对应的切削力约束;式(20)表示任一工序只能在一台机器上完成加工;式(21)表示任一工序的最早完工时间等于该工序所需的加工时间与该工序的最早开始时间之和;式(22)表示任一工序的最晚完工时间等于该工序的加工时间与该工序的最晚开始时间之和;式(23)表示同一工件的工序先后约束关系;式(24)表示机器的同一时刻只能加工一道工序;式(25)表示工序需在所选机器开机后才可进行加工;式(26)表示机器在完成了本机器加工的最后一道工序后即可关机;式(27)表示总工序长度;式(28)表示任一机床k都可以在零时刻开机;式(29)表示任一工序的最早开始时间;式(30)表示任一工序的最晚完工时间;
2 基于改进的离散化引力搜索算法的集成优化问题
万有引力搜索算法是RASHEDI等[14]学者在2009年受万有引力定律的启发,提出的一种新的群体进化算法,是根据物体与物体之间会在引力的作用下相互吸引的经典物理现象来构造的算法,其实现简单,收敛迅速,且具有较强的全局搜索能力,从提出至今已经在一系列复杂的连续优化问题的求解中取得了良好的效果。切削参数优化问题属于连续优化问题,而柔性作业车间调度问题属于离散优化问题,且柔性作业车间调度已被证实为NP-hard问题,将切削参数优化问题与柔性作业车间调度问题集成起来,无疑是复杂的NP-hard问题,采用一般的算法难以很好地解决该问题。
本文创新性地提出先使用改进的引力搜索算法优化每道工序在每个可选机器上加工的时间和碳排放,从得到单工序Pareto解集中挑选出5组合适的解定义为5种切削模式;在集成问题编码中,提出了一种基于三层信息的编码方式,第一层表示工序排序,第二层表示工序选用的机器,第三层表示工序在对应机器上选用的切削模式,以此来将切削参数离散化并集成到柔性作业车间调度问题中,最后提出一种改进的离散化引力搜索算法对集成问题进行求解。
2.1 切削模式Pareto解集求解
在实际的切削参数约束范围内,每道工序在每个可选机器上加工都可以选择不同的加工参数(切削速度Vc、进给量f),以得到不同的机床切削加工碳排放和切削加工时间,根据上述针对车间碳排放的分析,可得针对切削模式选择的多目标优化目标函数如下:
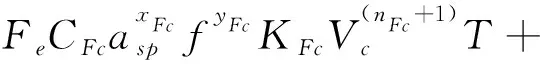
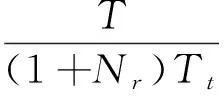
(31)
(32)
式(31)为单道工序在选择机器上加工产生的碳排放目标函数,式(32)为单道工序在选择机器上的加工时间目标函数。
采用笔者[13]提出的改进引力搜索算法对该多目标优化问题进行求解,得到对应的Pareto解集,从Pareto解集中挑选5组切削参数,对应工序在加工机器上的5种切削模式,即每一个工序在其可选的每一台加工机器上都各有5种切削模式,每种切削模式对应不同的加工时间和不同的机床切削加工碳排放,而切削模式对应的加工时间和机床切削加工碳排放是由切削参数组合决定的。
2.2 集成优化问题的编码与解码机制
编码是问题的基因表达式,在解决车间调度问题时至关重要。与传统的柔性作业车间调度问题不同,本文研究的切削参数与柔性作业车间调度问题集成优化问题,不仅考虑需工序排序和机器分配,还需考虑切削参数选用,无法沿用之前传统柔性作业车间调度问题的两层编码方式。
针对该集成优化问题的特点,本文提出一种基于三层信息的编码方式,该编码方式由三层独立的序列构成。如图1所示,第一层编码为工件序列编码,工件序列编码(3,2,2,1,3,1,2,1)表示首先加工工件3的工序1,再加工工件2的工序1,再加工工件2的工序2,以此类推;第二层编码为机器选择编码,机器选择编码(1,3,1,1,2,2,3,1)表示的是工件1的工序1在可选机器集合(M1,M2,M3)中选择M1进行加工,工件1的工序2在可选机器集合(M1,M2,M3)中选择M3进行加工,以此类推。第三层编码为切削参数模式选择编码,为了平衡求解速度和精确度,本文为每个工序对应的每台可加工机器提供了5种切削参数模式供选择,一种切削参数模式分别对应一组切削速度和进给量,切削参数模式编码(4,3,1,5,3,5,1,2)表示的是工件1的工序1在机器M1上选择切削参数模式P4进行加工,工件1的工序2在机器M3上选择切削参数模式P3进行加工,以此类推。

2.3 初始化方法
切削参数与柔性作业车间调度集成优化问题十分复杂,不仅要解决工序排序问题和机器选择问题,还要解决切削参数模式选择问题。因此不能盲目地使用随机生成的序列作为初始质点的序列,否则会严重影响求解的速度和求解效果。
目前,求解FJSP的文献进行初始化大部分采用的都是随机方法,初始种群的质量普遍不高,机器之间的负荷不平衡,为之后的优化带来较大难度。本文针对切削参数与柔性作业车间调度集成优化问题特性,提出以下几种初始化手段:
(1)在工序选择初始化方面
随机生成工件序列,如果生成的工件序列与初始种群中所有工件序列的汉明距离大于Nl,则将其加入初始种群中,否则重新生成。
(2)在切削参数模式选择初始化方面
提出了二元选择初始化方法。在二元选择初始化方法中工序编码随机生成,然后遍历每道工序对应的可选加工机器集合,在每台机器中随机选择两种切削参数模式,选择切削时间短的切削模式的概率为pc,否则选择碳排放量小的切削模式。
(3)在机器选择初始化方面
提出了基于当前工序完工时间的贪婪选择初始化和随机初始化结合的方法,即种群中比例为pm的个体采用基于当前工序完工时间的贪婪选择初始化方法进行初始化以改善初始种群的质量,而剩下的个体则采用随机初始化的方法以保证种群的多样性。在贪婪选择初始化方法中,遍历随机生成的工序序列编码中每道工序的所有可选机器集合,计算当前工序在所有可选机器上加工时的完工时间,贪婪选择使当前完工时间最短的机器。在随机初始化方法中,遍历随机生成的工序序列编码,随机选择可选机器集合中的一台机器作为加工机器。
2.4 多目标离散化引力搜索算法求解集成优化问题
本文针对切削参数与柔性作业车间调度集成优化问题,以最大完工时间和制造过程车间总碳排放为优化目标,提出了一种改进的离散化引力搜索算法(Improved Discrete Gravity Search Algorithm,IDGSA)。一般标准的引力搜索算法都是用来解决连续优化问题的,本文对引力搜索算法进行离散化并进行改进以适用于求解集成优化问题,在所提算法中,M表示质点质量,G表示万有引力常数,best 表示当前最好适应度,worst 表示当前最差适应度。首先,直接使用整数序列来表示工件序列编码、机器选择编码和切削参数模式选择编码。其次,加入多种初始化方法,在提高初始质点质量的同时保证了群体多样性。针对该集成优化问题的特点,对质点的加速度、速度以及位置的更新进行改进,以适应离散化求解需求。最后,针对三层编码特性提出了最优双层序列交叉策略,提高算法的寻优能力。
经典的引力搜索算法使用质点的质量来衡量质点的优劣,位置越好,质量越大,整个群体会朝着质量最大的质点移动,从而达到寻优的目的。离散化引力搜索算法与经典引力搜索算法相比,步骤基本相同,只需对其中部分操作重新定义。
(1)种群初始化
设置离散引力搜索算法的最大迭代次数为T,在约束范围内,按照上述种群初始化方法生成N个初始质点Si,在解空间中,任意一个解Si可以用3部分表示:
Si={Xi,Mi,Pi}。
(33)
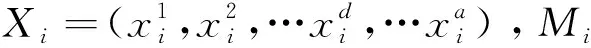
(2)适应度值及质点质量的计算
为了满足算法要求,需将目标函数CM和TCE进行整合,本文采用线性加权整合来计算适应度值。
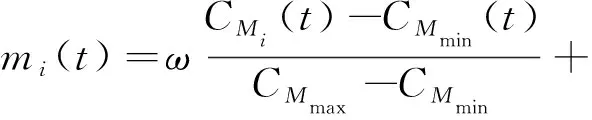
(34)
式中:ω为权重,CMi(t)和TCEi(t)为第t次迭代中第i个质点的完工时间和制造过程碳排放;CMmax和CMmin为完工时间优化函数中的最大值和最小值;TCEmax和TCEmin为制造过程中质点群中碳排放优化函数中的最大碳排放和最小碳排放。
质点质量计算如下:
(35)
式中N为种群大小。
(3)质点加速度计算
WANG等[15]提出一种简单有效的规则来解决离散问题中质点的更新问题。本文参考上述文章中的更新机制,针对切削参数与柔性作业车间调度问题的特点提出了一套类似的更新机制来解决种群中质点的更新问题。
首先,重新定义质点的加速度更新公式:
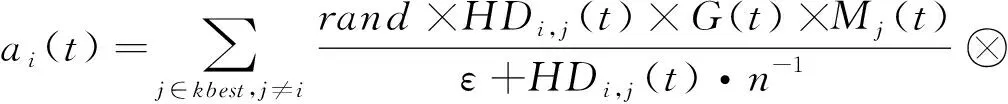
(36)
式中:rand表示在[0,1]区间服从均匀分布的随机变量;i,j∈{1,2,……,N},且i≠j;ε为一个常数;HDi,j(t)为第t次迭代时第i个质点的工件序列和第j个质点的工件序列的汉明距离;xj(t)为第t次迭代时第j个质点的工序编码;xi(t)为第t次迭代时第i个质点的工序编码。
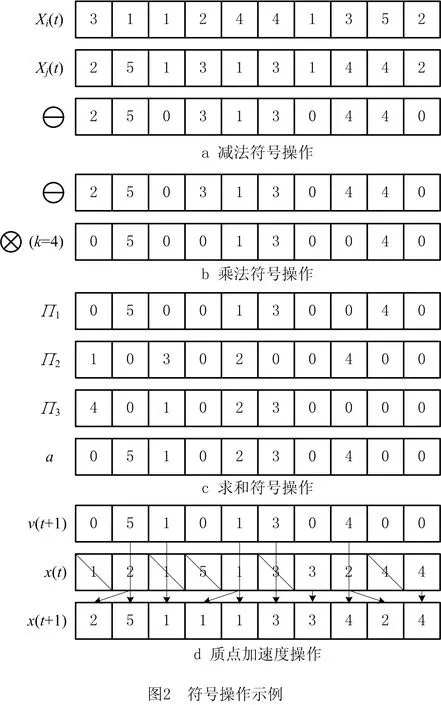
式(36)中的特殊符号操作解释如下:
1)减法符号⊖
若序列xi(t)中第j个位置上的值与序列xj(t)上的相同,则第j个位置上的值被置为0;否则,将被置为xj(t)的值。具体操作细节如图2a所示。
2)乘法符号⊗

(37)
在工件序列中随机选择k个非零元素保持不动,其余元素置0。具体操作细节如图2b所示。
3)求和符号∑
求和操作就是将进行了减法操作和乘法操作之后的kbest个序列组合成一个加速度序列。具体操作细节如图2c所示,即遍历加速度序列,将加速度序列第i个位置的值置为kbest个序列中随机挑选的一个序列的第i个位置的值。
(4)质点速度及位置更新
速度更新公式:
vi(t+1)=ai(t)⊙vi(t)。
(38)
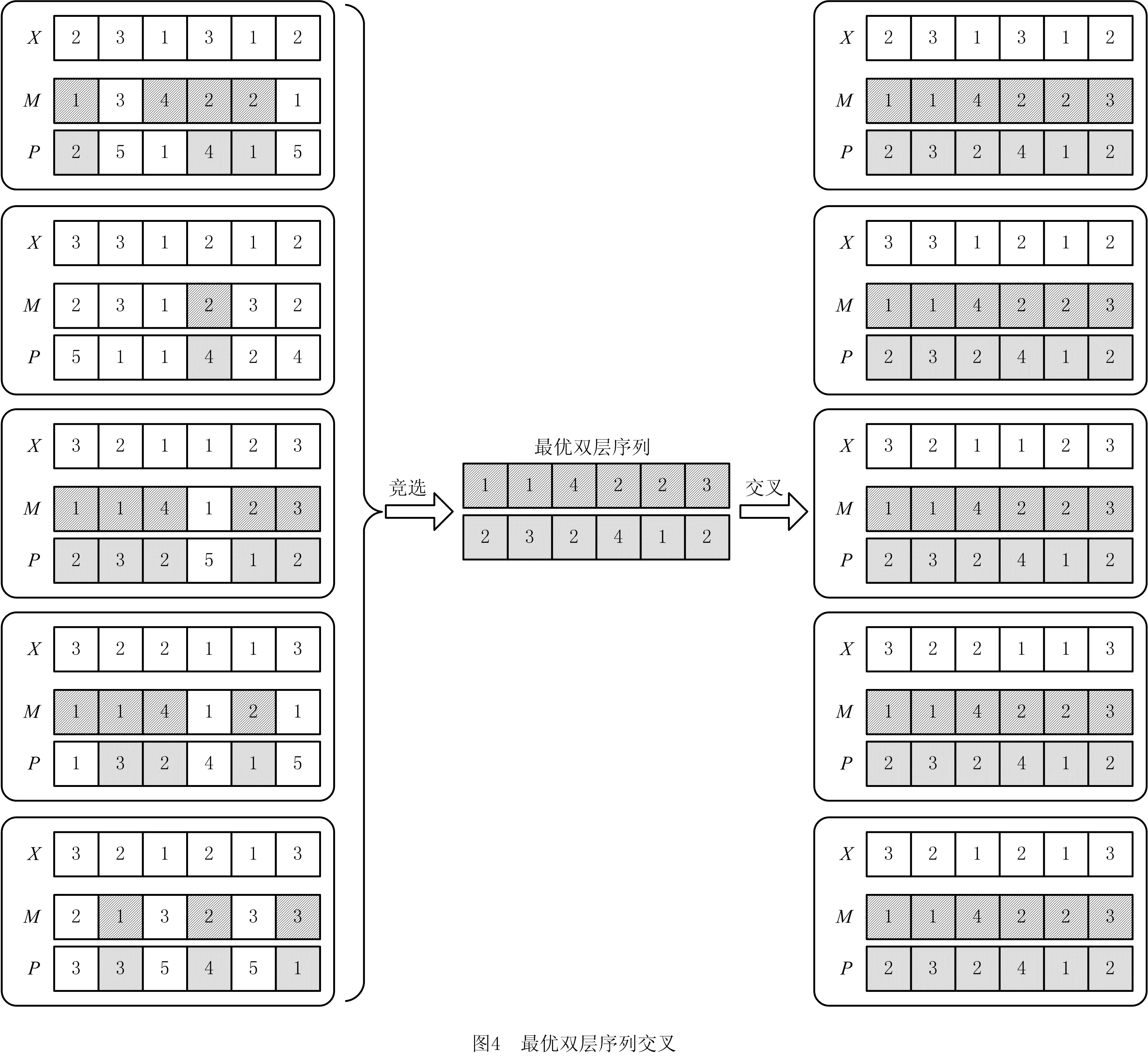
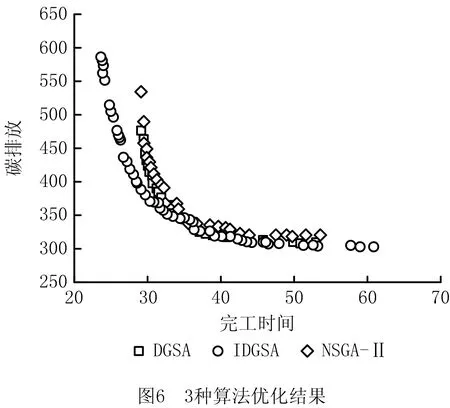
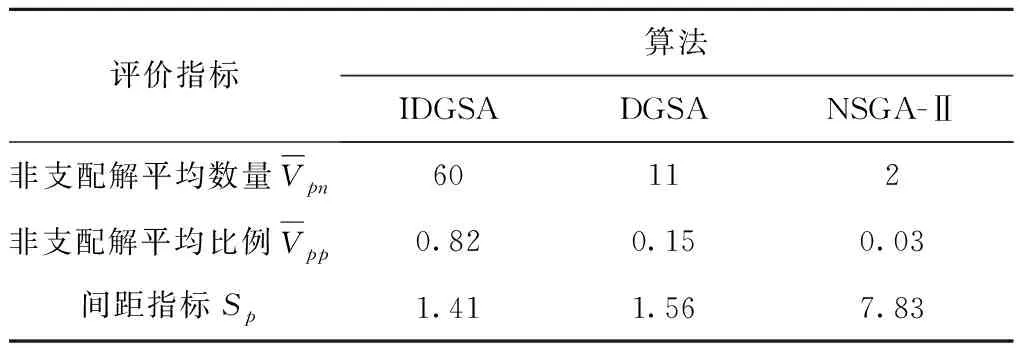
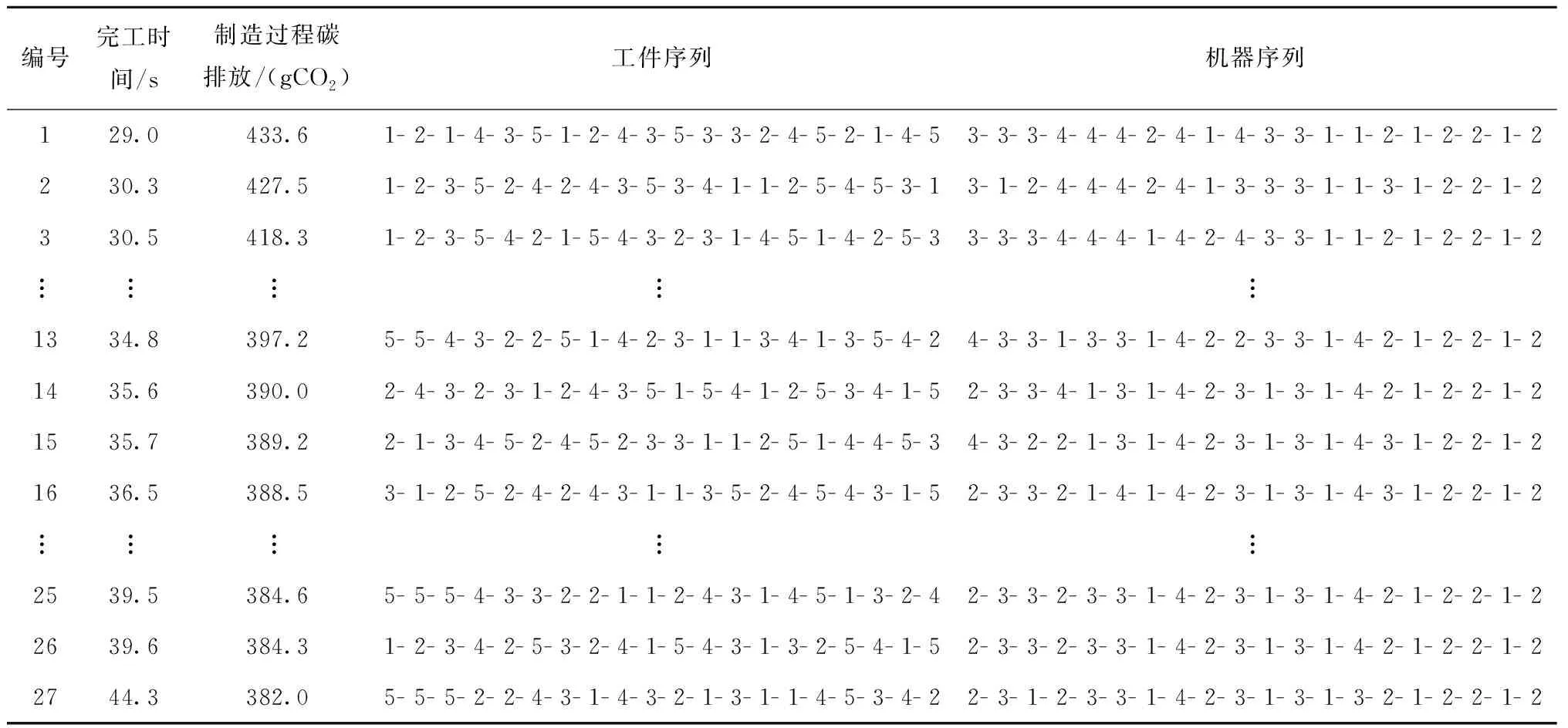
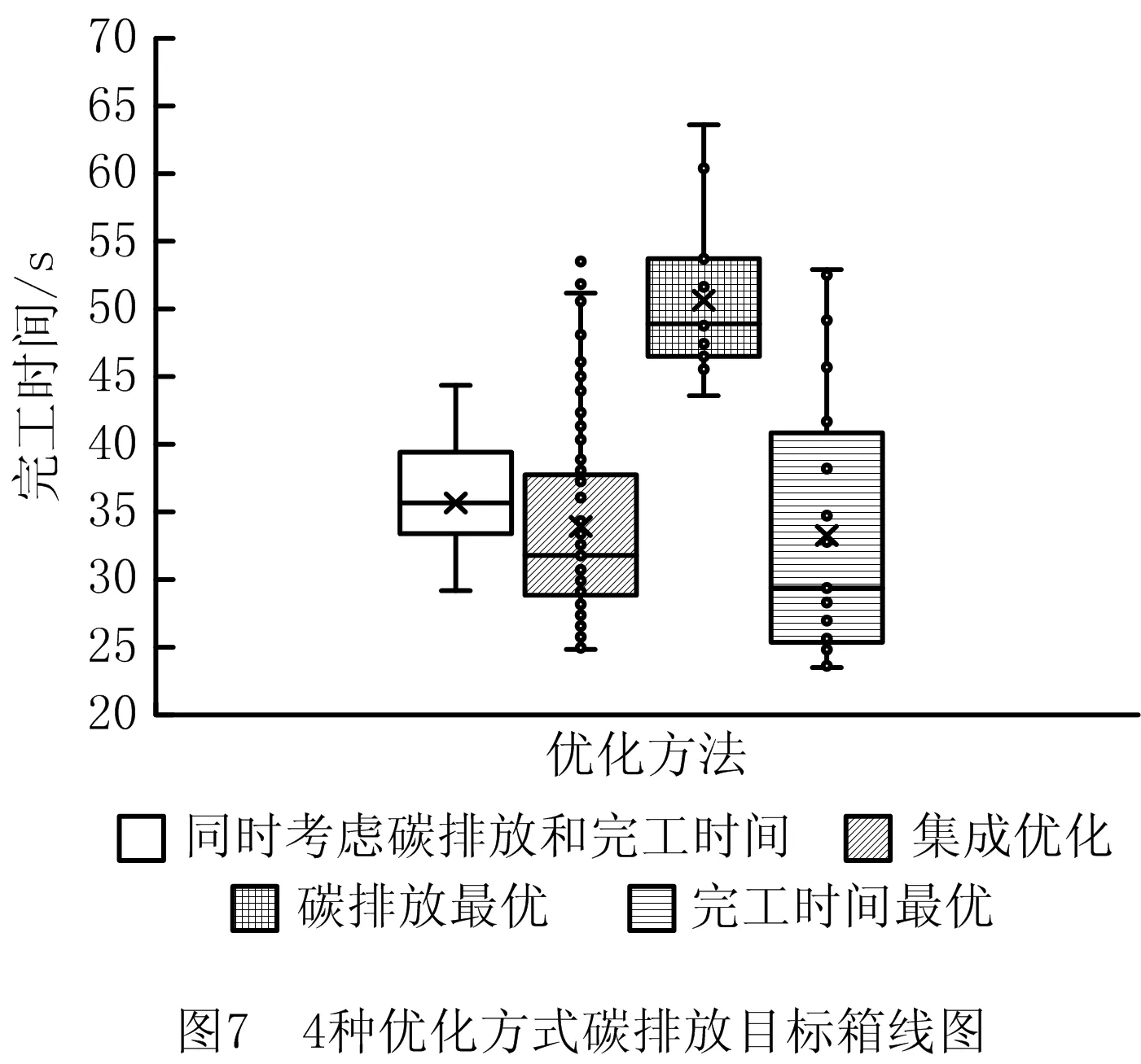
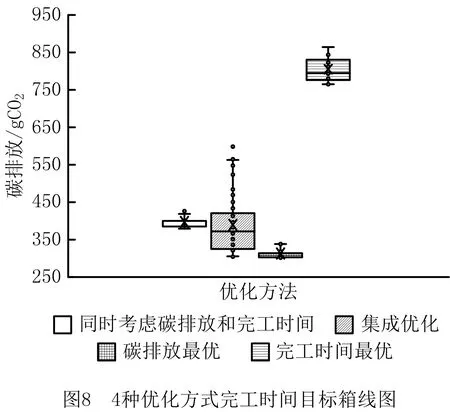
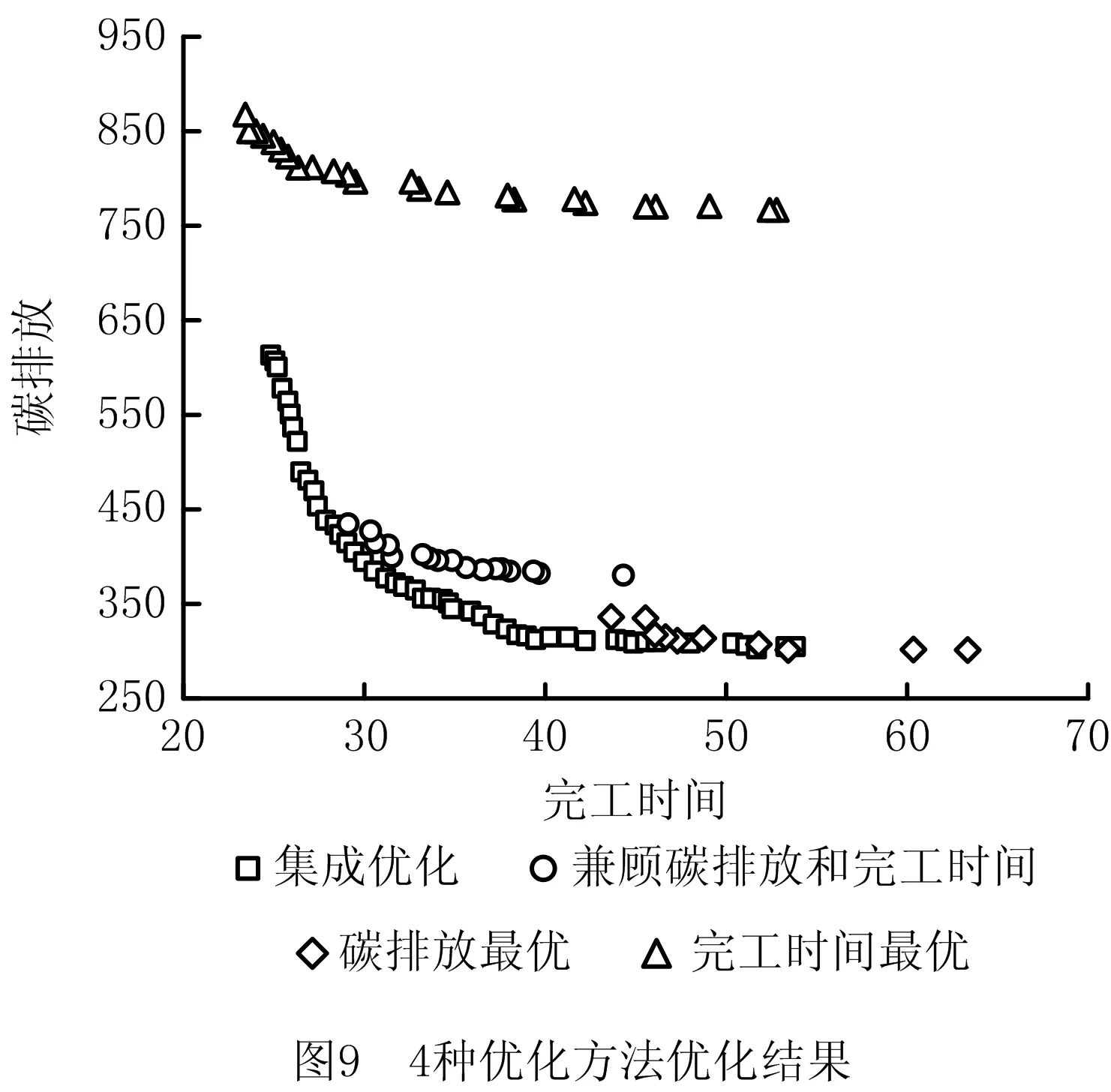
符号⊙表示质点速度序列的更新操作方式,具体更新操作如下:记randj为在[0,1]区间服从均匀分布的随机变量,常数∂的取值区间为(0,1)。若常数∂ 位置更新公式: xi(t+1)=vi(t+1)⊕xi(t)。 (39) 符号⊕表示质点工序序列的更新操作方式,具体的更新操作如下:保留vi(t+1)序列上的非0元素到xi(t+1)上,删除xi(t)序列上与vi(t+1)序列相同的工序,并将xi(t)序列剩余的元素依次填充到xi(t+1)序列的空缺中。 (5)机器选择序列及切削模式选择序列的更新 以上操作除种群初始化以外,都是只涉及工序序列的更新操作。而机器选择序列和切削模式选择序列对于优化结果的影响同时也十分巨大。因此,本文采用多父辈交叉(Multi-Partent Crossover,MPX)方法对机器选择序列进行优化,并采用变邻域搜索方法对切削模式选择序列进行了优化。 1)MPX交叉操作对机器选择序列进行更新。 采用MPX交叉操作对机器选择序列进行交叉,如图3所示。具体交叉步骤如下:首先随机生成一条由0或者1组成的序列U,序列U的长度与机器选择序列相同,其中1的个数不能超过序列长度的1/3。互换父代序列Mi(t)和Mj(t)中与序列U中元素1位置相同的元素,得到子代序列Mi(t+1)和Mj(t+1)。因为互换的机器都属于同一道工序的可选机器集合,保证了互换后子代序列依然是可行解。注意在交叉机器序列的同时,需要将切削模式序列也进行对应的交叉。 互换后产生的子代机器选择序列并不一定优于父代序列,极有可能出现退化现象,即新产生的质点劣于原质点。为减少算法的退化现象,引导群体向真实的Pareto前沿前进,在模拟退火算法思想的启发下,本文提出了机器选择更新回退策略: (40) (41) 其中:P1为机器选择更新率;Safter≻Sbefore表示更新后的质点支配更新前的质点;Pk为常数,0 2)变邻域搜索进行切削模式选择更新。 变邻域搜索算法从一个初始解开始,通过搜索不同邻域来提高求解质量,同时邻域范围的不断增大使得算法具有跳出局部最优的能力。该算法简单有效,已经在算法优化领域得到了成功的应用[16-18]。本文使用变邻域搜索对切削模式选择进行更新。 首先定义两个邻域:①邻域N_1,在切削模式中随机选择除当前模式以外的两个模式,则设置比较两个模式的机床切削碳排放,选择机床切削碳排放更小的模式;②邻域N_2,在切削模式中随机选择除当前模式以外的两个模式,比较两个模式的工序切削加工时间,选择工序切削加工时间更小的模式。 使用变邻域搜索对切削模式选择进行更新,具体步骤如下: 步骤1依次遍历切削模式序列,使用邻域N_1得到新的质点S′,如果新的质点S′成功支配原先的质点S,则使用新的质点替代原先的质点,即令S=S′,然后再重头开始遍历切削模式序列,否则继续遍历。 步骤2依次遍历切削模式序列,使用邻域N_2得到新的质点S′,如果新的质点S′成功支配原先的质点S,则使用新的质点替代原先的质点,即令S=S′,然后再转到步骤1重新遍历,否则继续遍历。 步骤3输出最优的质点S。 (6)三层编码模式交叉 更新种群中所有质点的两个目标函数,使用非支配排序进行排序,并计算质点的拥挤距离,建立偏序关系,当质点满足以下两个条件之一时: I[i]rank (42) I[i]rank=I[j]rank&&I[i]distance>I[j]distance。 (43) 称第i个质点支配第j个质点,即I[i]I[j],其中I[i]rank为第i个质点的非支配等级,I[j]rank为第j个质点的非支配等级,I[i]distance为第i个质点的拥挤距离,I[j]distance为第j个质点的拥挤距离。 偏序关系建立后,本文提出一种新的竞选机制,竞选出最佳的机器序列和切削参数序列,将采用这种方法得到的两个序列称为最优双层序列,并将其与精英质点组合得到新的质点,如图4所示,具体步骤如下: 步骤1从种群中挑选出非支配等级最高的所有质点,称为精英质点。 步骤2遍历所有精英质点的机器序列M的每个位置,投票竞选出每个位置的最佳机器,即选择每个位置出现次数最高的机器,如果出现次数最高的机器不止一个,随机选择其中一个即可。 步骤3由机器序列位置所选机器与最佳机器序列位置所选机器相同的精英质点投票竞选出每个机器位置的最佳切削参数选择,即选择每个位置出现次数最高的切削参数模式,如果出现次数最高的切削参数模式不止一种,随机选择其中一种即可。 步骤4将最佳机器序列和最佳切削参数选择序列组合成最优双层序列。 步骤5将最佳机器序列和所有精英质点的工件序列交叉组合成新的质点,并将新的质点加入种群中。 (7)更新种群 更新种群中所有质点的两个目标函数,合并新的种群与原来的种群,使用非支配排序后再根据精英保留策略保留90%的支配等级高的精英质点,并且保留10%的普通质点构成新的群体。算法流程图如图5所示。 为了验证集成优化研究的优越性以及所提改进算法的有效性,本文根据实际制造车间生产数据,产生一组切削参数与柔性作业车间问题集成实例(见附录)。在该实例中,制造车间共生产5个不同的工件,每个工件均有4道工序,每道工序均有4台可选机器,每个工序对应的每台机器均有5种切削模式可供选择。 为验证所提改进算法的有效性,分别采用本文提出的IDGSA和DGSA、改进的非支配排序遗传算法(NSGA-Ⅱ)对上述实例进行求解。为了公平起见,所有算法均采用C++语言进行编程并在Ubuntu 16.04操作系统上运行。以上3种算法的具体参数设置如下: (1)IDGSA,种群规模为200,最大迭代次数为500,汉明距离差异Nl=2,机器选择初始化比例pm=0.6,切削模式初始化比例pc=0.4,权重ω=0.4,速度更新常数∂=0.7,常数Pk=0.3。 (2)DGSA,除了无需设置切削模式初始化比例pc,其余参数与改进的离散引力搜索算法一致。 (3)NSGA-Ⅱ,种群规模为200,最大迭代次数为500,交叉概率为0.7,变异概率为0.1。 使用上述3种算法优化本文提出的集成优化多目标函数。图6为IDGSA、DGSA、NSGA-Ⅱ三种算法的Pareto最优前沿。 由图可知,3种算法的Pareto前沿分布都较为均匀,说明这3种方法对于求解集成优化问题都有一定的效果。DGSA得到的Pareto前沿相较NSGA-Ⅱ得到的Pareto前沿更加靠近Pareto最优前端,而NSGA-Ⅱ的Pareto前沿分布更广,两种算法得到的结果并没有明显的差距。而本文提出的IDGSA得到的Pareto解集不但均匀分布在Pareto前端,而且分布范围更广,该算法得到的Pareto解集成功支配了其他两种算法得到的绝大部分解,说明了该改进算法获得的群体多样性更优,算法寻优能力更强。 为了进一步比较3种算法的优劣,本文引入了非支配解数量Vnp、非支配解比例Vrd和间距指标Sp三种多目标算法评价指标。设参与比较的算法i求得的Pareto解集为Bi,将所有参与比较的算法求得的Pareto解集合并的总解集称为Bt,然后将对总解集Bt进行非支配排序所得的Pareto解集称为参考集Bp。 (45) (3)间距指标Sp衡量算法获得的Pareto解集的分布程度,该指标值越小,说明算法得到的Pareto解集分布性越好。算法i的间距指标Sp的求解公式如下: di=min(|f1(xi)-f1(xi)|+|f2(xi)-f2(xi)|),j≠i; (46) (47) 其中:f1(xi)是解xi的第1个目标值,f2(xi)是解xi的第2个目标值。 3种算法的评价指标结果如表2所示。 表2 3种算法的评价指标结果 由表2可知,DGSA得到的非支配解平均数量和非支配解平均比例都远远大于其他两种算法,证明了针对三层编码问题特性提出的变邻域搜索和最优双层序列交叉能够引导算法向Pareto真实前端靠近。IDGSA得到的非支配解的间距指标Sp稍小于DGSA算法,且明显低于NSGA-Ⅱ的间距指标值,说明本文所提的多种初始化方法和交叉策略提高了离散化引力搜索算法群体的多样性。 为证明本文所提集成优化方式的优越性,需要将其与传统的优化方式进行对比。因此,本文将其与面向低碳的切削参数不可变的调度优化方法进行比较,总共对比3种切削参数不可变的情形,分别采用碳排放最低的切削参数组合、完工时间最优的切削参数组合和同时考虑碳排放和完工时间的切削参数组合。 碳排放最优的切削参数不可变方法指根据单工序的多目标优化目标函数求解出单工序在每台可加工机器上的Pareto解集,从求得的Pareto解集中挑选出碳排放最优的参数组合作为工序对应加工机器的切削参数组合,并在调度优化过程中不再变化,而完工时间最优的切削参数不可变方法从Pareto解集中挑选的是完工时间最短的参数组合,同时考虑碳排放和完工时间的切削参数不可变方法挑选的是碳排放和完工时间都适中的参数组合。 本文提出的切削参数可变的集成优化方法是从Pareto解集中挑选出5组参数组合,包括完工时间最短的参数组合、碳排放最优的参数组合和另外3组分布均匀的参数组合,作为单个工序对应可加工机器的切削模式,在后续的调度优化中通过选用不同的参数组合进一步优化。4种优化方式具体的优化结果如表3~表6所示。 表3 碳排放最优的切削参数不可变优化结果 表4 完工时间最优的切削参数不可变优化结果 续表4 表5 同时考虑碳排放和完工时间的切削参数不可变优化结果 表6 切削参数可变的集成优化结果 由表3~表6可知,碳排放最优的优化方法得到的完工时间和制造过程碳排放结果范围为{[43.6,63.4],[302.5,338.1]},完工时间最优的优化方法得到的结果范围为{[23.3,52.8],[765.7,865.6]},同时考虑碳排放和完工时间的优化方法得到的结果范围为{[29.0,44.3],[382.0,433.6]},而切削参数可变的集成优化方法的结果范围为{[24.9,60.8],[303.4, 614.0]}。结合表3~表6、图7和图8,可知切削参数不可变的3种方法的优化空间都显著小于切削参数可变的集成优化方法的优化空间,而且切削参数可变的集成优化方法其Pareto解集分布更加均匀。 绘制4种优化方法的Pareto解集散点图如图9所示。由图9可知,完工时间最优的切削参数不可变优化方法虽然得到了少数几个比集成优化更低的完工时间的解,但是其碳排放相比切削参数可变的集成优化方法却提高了将近一倍,在完工时间最优的切削参数不可变优化方法中,单道工序在其选择的加工机器上使用了Pareto解集中加工时间最短的切削参数组合,较低完工时间的切削参数组合通常会伴随较高的碳排放,在单工序上一味追求最短的加工时间,势必会产生大量的碳排放。碳排放最优的切削参数不可变优化方法,其制造过程的最低碳排放基本与切削参数可变的集成优化方法持平,然而其完工时间普遍偏大,且其Pareto解集数量稀少,呈零散分布。兼顾碳排放和完工时间的切削参数不可变方法无法得到加工时间较小的解或碳排放较优的解,其Pareto解集几乎全部被切削参数可变的集成优化方法得到的Pareto解集支配。切削参数可变的集成优化方法得到的Pareto前沿分布均匀且广阔,成功支配了切削参数不可变的3种优化方法的绝大多数解,明显优于其他3种切削不可变的优化方式。在未来工作中将进一步研究考虑加工质量、成本和效率的切削参数与柔性作业车间调度集成低碳建模与优化。 本文针对柔性作业车间调度问题,以制造过程碳排放和最大完工时间为优化目标,将可变切削参数与柔性作业车间调度问题优化集成起来,首次提出了工件序列—机器序列—切削参数模式三层编码。针对集成优化问题特性,对离散化引力搜索算法存在的缺陷进行改进,设计了一种改进的离散化引力搜索算法对其求解,改进算法采用多点交叉和变邻域搜索,针对三层编码特性提出了一种新的竞选机制,竞选出最优双层序列,与精英质点的工件序列交叉产生新的质点,提高了算法的寻优能力,引导种群向真实Pareto前沿靠近。通过对比NSGA-Ⅱ和DGSA,验证了改进算法的优越性。最后将本文所提切削参数可变的集成优化方法与3种切削参数不可变的优化方法进行对比,证明了集成优化方法更广的优化空间。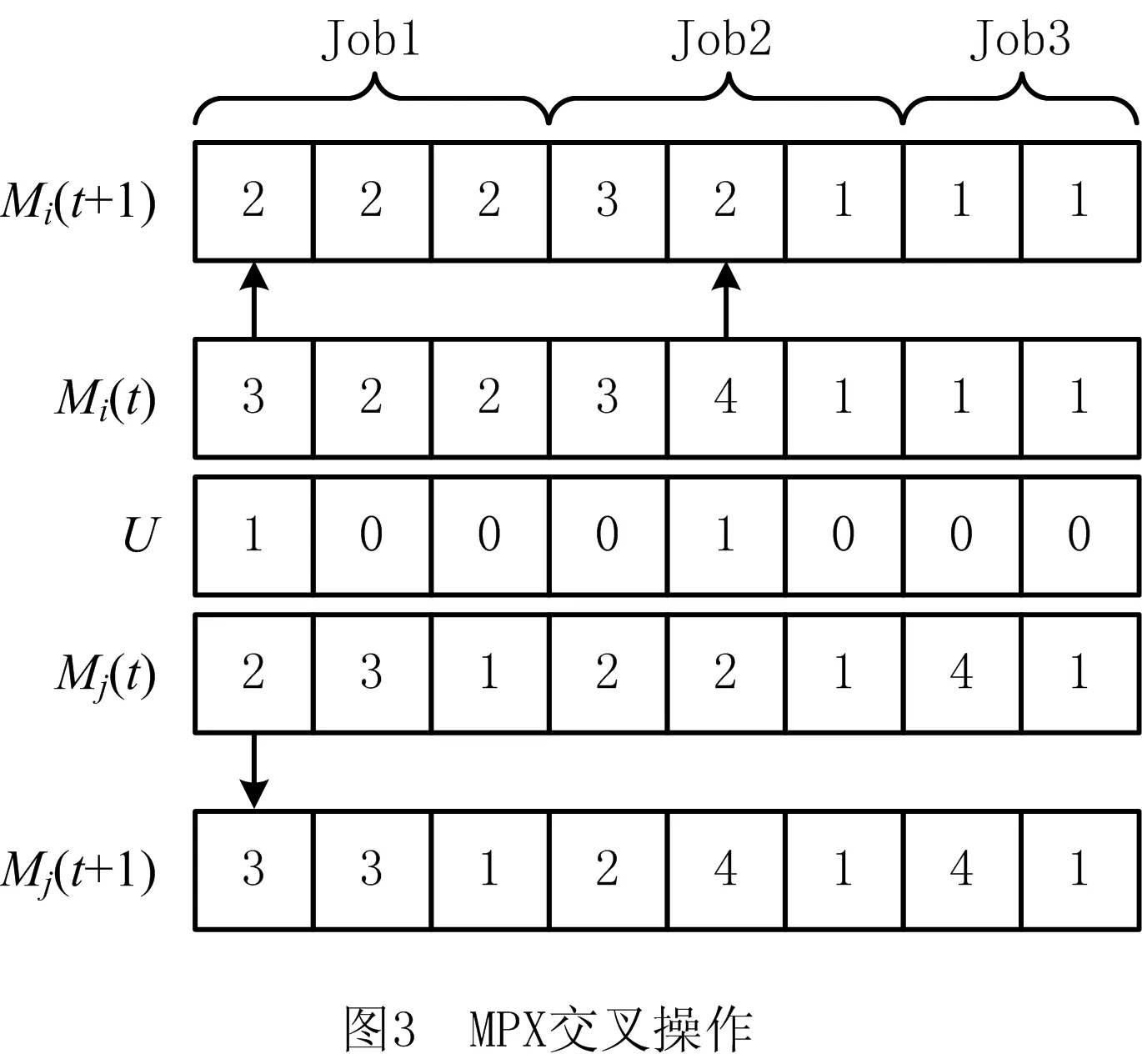

3 实验结果与分析
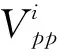
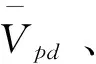




4 结束语
