耦合模糊C均值聚类和贝叶斯网络的遥感影像后验概率空间变化向量分析

李轶鲲， 杨 洋， 杨树文,3， 王子浩

(1.兰州交通大学测绘与地理信息学院，兰州 730070; 2.地理国情监测技术应用国家地方联合工程研究中心，兰州 730070； 3.甘肃省地理国情监测工程实验室，兰州 730070)

0 引言

快速、有效和经济地监测地表变化已成为学术界研究的热点问题，遥感变化检测是非常有效的解决技术手段之一[1-3]。目前，遥感变化检测技术面临的最大挑战是来自自然环境和遥感波谱相互作用的复杂性所造成的不确定性。这种不确定性不但使得传感器记录的地表光谱信号易于出现混合像素现象[4]，而且也对影像变化检测过程中的各个环节产生了不利影响，从而降低了变化检测最终结果的精度[5-7]。为此，Chen等[8]通过研究分类后比较法(post classification comparison，PCC)和变化向量分析(change vector analysis，CVA)的优缺点[9]，提出了后验概率空间变化向量分析(change vector analysis in posterior probability space，CVAPS)法。该方法能够有效缓解PCC容易受累计分类误差影响的问题[10]，且与CVA不同，CVAPS不需要良好的辐射校正。然而，CVAPS算法使用支持向量机(support vector machine，SVM)估计后验概率向量，没有专门针对遥感影像中易于出现的混合像素现象进行建模，因而容易造成变化检测精度的损失。

针对混合像元问题，模糊聚类算法[11]能够以不同的隶属度将遥感影像像元与不同信号类[12]联系起来，有效解决混合像元的分解。其中，信号类指得是遥感影像中具有典型光谱或纹理特点的像素组成的聚类。由此，本文采用模糊C均值聚类(fuzzy C-means，FCM)对遥感影像进行聚类，原因为： ①FCM是一种无参数算法，其对遥感影像数据的统计分布没有要求； ②由于FCM计算出的模糊隶属度与信号类在影像中的比例强相关, 因而将隶属度作为混合像素中的相应信号类的概率是比较合理的。然而，FCM从遥感影像中提取的信号类与影像中的地物并没有直接的一一对应关系[13]。例如，城市区作为一种地物，其本身由建筑物、绿地、道路等子地物构成，而与这些子地物对应的信号类与城市区形成了多对一的对应关系。又比如，森林中的阴影与水体有着类似的光谱特点，因而很可能被划分成同一信号类，证明同一信号类在不同环境下可能与多种地物形成一对多的关系。因此，需要使用相应的数学模型对信号类与地物间的多对多的关系进行建模，而简单贝叶斯网络(simple Bayesian network, SBN)可以很好地解决这一问题[14-15]。基于以上分析，本文使用FCM为SBN提供关键参数，以计算遥感影像中像素属于各个地物的后验概率向量，提出了一种新的后验概率空间变化向量法： FCM-SBN-CVAPS。该方法的优点在于： ①使用FCM的模糊隶属度，为SBN估计像素属于各个信号类的条件概率； ②提出了新的SBN学习模型，利用模糊隶属度为SBN估计所涉及地物中个信号类的条件频率。

1 耦合FCM的SBN分类模型构建

1.1 耦合FCM的SBN模型

为解决遥感影像混合像元建模问题，本文设计了一种SBN模型，将FCM从遥感影像中发现的信号类与遥感影像中存在的地物建立随机链接。SBN模型与FCM的结合体现在两方面： ①使用FCM计算的模糊隶属度建立遥感图像中某像素pi,j与信号类ωk间的随机链接，缓解了混合像元现象； ②基于模糊隶属度和地物Lv的训练样本，建立信号类ωk与地物Lv间的随机链接，解决了信号类与地物间的多对多关系的建模问题。本文使用的SBN模型如图1所示。

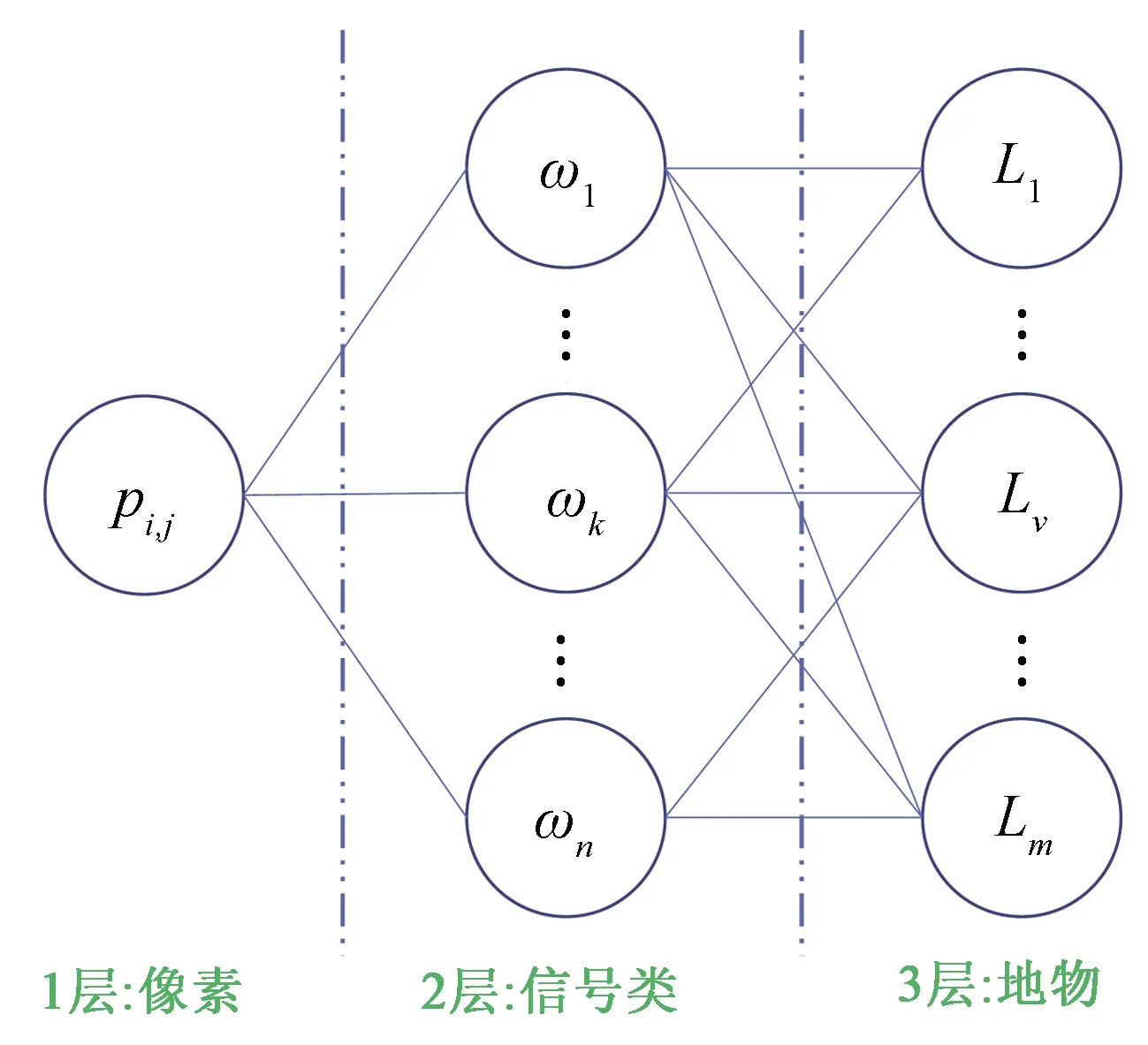
图1 简单贝叶斯网络Fig.1 Simple Bayesian network

该模型共3层： 第一层为遥感影像的像素，其中pi,j为位于该影像i行j列的像素； 第二层为信号类，其中ωk为遥感影像中具有某种典型光谱或纹理特征的像素所构成的信号类或聚类； 第三层为遥感影像中的地物，其中Lv为该影像中的某一类地物。通过该模型，能够计算出像素pi,j属于地物Lv的后验概率P(Lv|pi,j)。根据贝叶斯网络的计算原则，P(Lv|pi,j)可以通过以下公式计算：

(1)

根据贝叶斯公式，P(Lv|ωk)可表示为：

(2)

进一步，将式(2)代入式(1)可得:

(3)

式中：P(ωk|pi,j)为像素pi,j属于信号类ωk的程度, 可由FCM计算得到(详见2.2节)；P(ωk|Lv)为地物Lv中信号类ωk发生的概率(估计方法详见2.3节)；P(Lv)为地物Lv的先验概率；P(ωk)为信号类ωk的概率。综上所述，通过式(3)，最终可以计算出像素pi,j属于遥感影像中各个地物Lv(v=1,…,m)的后验概率向量ρ=(ρ1,…,ρv,…,ρm)(其中ρv=P(Lv|pi,j))，实现后验概率空间变化向量框架下的变化检测。

1.2 模糊C均值聚类模糊隶属度计算

在中低分辨率遥感影像中，混合像元普遍存在，单一像元可能隶属于多个信号类。为此，本文使用FCM以不同的隶属度将像元与不同信号类联系起来，有效的实现了混合像元的分解，以提高后续处理过程的精度。

设影像I={pi,j|1≤i≤N, 1≤j≤M}是由N行M列像素构成的遥感影像，现将其模糊划分为n个信号类，uk(i,j) (1≤k≤n)表示图像I中像素pi,j对于第k个信号类ωk的隶属度。隶属度集合U={uk(i,j)}满足如下约束条件：

(4)

FCM聚类算法采用各个像素与所在信号类中心的差值平方和最小准则，通过迭代更新隶属度集合U和信号类中心Ψ，达到使目标函数J最小的最优聚类，目标函数J的定义如下：

(5)

式中：Ψ={ψ1,…,ψk,…,ψn}为信号类中心点集，且ψk是信号类ωk的中心；q为控制聚类模糊程度的模糊参数。从式(4)可以看出，SBN中P(ωk|pi,j)与uk(i,j)满足同样的约束条件，因此可以用FCM计算所得的uk(i,j)估计P(ωk|pi,j)，实现SBN与FCM的结合。

1.3 基于模糊隶属度的SBN学习

为了计算像素pi,j属于地物Lv的后验概率P(Lv|pi,j)，需要基于专家提供的地物Lv的训练像素集合Tv以计算条件概率P(ωk|Lv)。论文首先定义地物Lv中信号类ωk的频率公式为：

SFv(k)=∑uk(x,y)∀px,y∈Tv

(6)

由于不同于普通聚类算法如K均值聚类，训练像素px,y关于信号类ωk的隶属度不是0或1，而是属于0，1之间的一个模糊隶属度uk(x,y)，因此需要对训练集Tv里的所有像素对信号类ωk的隶属度求和来计算地物Lv中信号类ωk的频率。

在计算出训练集Tv中所有信号类ωl(l=1,…,n)的频率SFv(l)后，条件概率P(ωk|Lv)被近似为：

(7)

另外，在式(3)中，先验概率P(ωk)是计算后验概率P(Lv|pi,j)的归一化因子。本文使用全概率公式计算P(ωk)，即

P(ωk)=∑vP(ωk|Lv)P(Lv)

(8)

式中P(ωk|Lv)可以通过式(6)和(7)进行估计。

1.4 后验概率空间变化向量

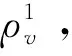
Δρ=ρ1-ρ2

(9)

式中Δρ为像素pi,j在t1和t2时相的后验概率的变化向量。相应的，像素pi,j在后验概率向量空间的变化幅度为：

(10)

最后，使用自动阈值算法对基于式(10)生成的变化幅度图进行处理，得到变化二值图。

1.5 FCM-SBN-CVAPS检测模型

综上所述，构建的FCM-SBN-CVAPS变化检测算法的主要流程如图 2所示。

图2 耦合模糊C均值聚类和贝叶斯网络的变化检测模型Fig.2 Change detection model coupling fuzzy C- means clustering and Bayesian network

2 实验结果及分析

基于构建的FCM-SBN-CVAPS模型，论文进行了变化检测、参数敏感性测试、训练样本数量影响分析、算法耗时分析及综合性能比较等方面的测试实验。

本文以甘肃省兰州市兰州新区为研究区。研究区位于兰州市北部，东南与兰州市皋兰县毗邻，西北与兰州市永登县相邻，中心位置为E103°290′～103°49′，N36°17′～36°43′。研究区主要包括建筑物，农田，森林，荒地，山地等地物类型。本实验选择了2016年和2017年的两景Landsat8影像，影像大小为650像素×650像素。对实验数据做了辐射定标、大气校正及图像拉伸等预处理。实验系统的运行环境为英特尔 Core i7-10700 2.90GHz 8核处理器。为提高精度，实验中对生成的初始变化二值图都进行了去噪处理和形态学闭运算(填充空洞)处理。

2.1 变化检测示例

为验证所提出算法的有效性，本文实现了基于SVM的CVAPS算法(简称SVM-CVAPS[8])，并与FCM-SBN-CVAPS算法对比。其中FCM-SBN-CVAPS为50信号类，模糊参数q=3.5,5 000训练样本/地物，阈值算法为Otsu； SVM-CVAPS为5 000训练样本/地物, 阈值算法为Kapur[15]。结果如图3所示。通过对比，从中可直观地观察到FCM-SBN-CVAPS算法和SVM-CVAPS算法变化检测性能的差异。其中，图3(c)中红线划分的区域为人工检测到的变化区域。图3(d)和图3(e)中红线划分的区域分别为FCM-SBN-CVAPS算法和SVM-CVAPS算法检测到的变化区域。图3(d)和图3(e)中蓝色框内为算法错检的变化区域。从图中可以发现，相比FCM-SBN-CVAPS算法，SVM-CVAPS算法错检区域范围明显更大。图3(c)中黄框内为两个算法都漏检的区域，而绿框内为SVM-CVAPS算法漏检的区域。因此，与FCM-SBN-CVAPS算法相比SVM-CVAPS算法漏检的区域更多一些。

(a) 2016年影像(b) 2017年影像(c) 人工检测到的变化结果

2.2 算法参数敏感性测试

论文使用FCM对影像的7个波段进行聚类处理。首先，为FCM设定3种不同聚类数(10,30及50)和6种不同模糊参数q(1.0,1.5,2.0,2.5,3.0,3.5,4.0)，以测试其对最终变化检测结果的影响。其中，当q=1.0时，FCM退化为普通C均值聚类。另外，本实验从原始图像中选取了5类地物作为训练样本： 建筑物(29 326像素)，农田(19 926像素)，森林(80 120像素)，荒地(32 224像素)，山地(144 312)。总训练像素数量为305 908(约占实验图像总像素的36.20%)，每种地物的平均训练像素数量为61 182。

具体实验结果如图4所示。从实验结果可发现： 当模糊度参数q=1.0及1.5时，FCM模糊度不够，无法有效反映Landsat8影像的混合像元现象，因而导致在所有聚类数下，变化检测Kappa系数值较低(均不超过0.50)。特别是当q=1.0时FCM退化为普通C均值聚类，Kappa系数均不超过0.40。当模糊参数q大于等于2.0时，对于所有聚类数，变化检测Kappa系数均大于0.75，并且随着q的继续增大，Kappa系数没有显著变化。以上结果表明混合像元问题极大地影响变化检测精度。

图4 基于不同聚类数和模糊参数q的FCM-SBN-CVAPS算法的Kappa系数Fig.4 The Kappa coefficient of FCM-SBN-CVAPS algorithm based on different clustering number and fuzzy parameter q

2.3 训练样本数量对Kappa系数影响

为了比较不同数量训练样本对FCM-SBN-CVAPS算法的影响，针对每类地物随机选取了1 000，2 000，3 000，4 000和5 000个训练像素。相应的，总训练像素数分别约占实验图像总像素的0.59%，1.18%，1.76%，2.37%，2.96%。实验结果如图5所示，图上每种聚类数的模糊参数q选用图4中具有最佳Kappa系数的模糊参数值。进一步分析表明： 训练样本数量对变化检测的Kappa系数的影响很微弱，训练样本为1 000时与训练样本为5 000时的Kappa系数值的差异分别为0.02(聚类数10)，0.00(聚类数30)，0.00(聚类数50)。因此，本文所提出的方法只需要较少的训练样本就可以取得相对较好的变化检测效果。并且，随着训练样本的增加，Kappa系数没有明显下降，足见本文所提方法对过度训练问题有较好的鲁棒性。

图5 不同数量训练像素对FCM-SBN-CVAPS及SVM-CVAPS算法Kappa系数的影响Fig.5 Effects of different number of training pixels on the Kappa coefficients of FCM-SBN-CVAPS and SVM-CVAPS algorithms

为了进一步通过比较验证所提出算法的有效性，实验测试了SVM-CVAPS算法在不同数量训练样本条件下的变化检测性能，结果如图5所示。结果表明，随着训练样本的增加，SVM-CVAPS算法的Kappa系数没有明显改善，甚至有时增加训练样本后Kappa系数出现下降现象。训练样本为1 000时与训练样本为5 000时的Kappa系数值的差异为0.04。与本文提出的FCM-SBN-CVAPS算法相比，SVM-CVAPS算法对训练样本数量更为敏感，且这种影响并不总是正向的。造成这一结果的原因可能在于： ①训练样本选择对SVM的分类性能有较大的影响，而本实验的训练像素是从手动划分的训练区域中随机选取的； ②相比其他分类器，SVM在小样本条件下具有更好的鲁棒性[8]，因此样本的增加不一定会导致更好的分类性能。

2.4 算法耗时分析

FCM是FCM-SBN-CVAPS算法中最为耗时的步骤，并且随着聚类数的增加，FCM所消耗的时间有极大的增长。其后继SBN训练和变化检测所消耗时间则少得多，并且与训练像素的数量没有明显的关系。相比之下，SVM-CVAPS算法中训练和分类步骤消耗了最多的时间，耗时与训练样本数正相关，而其变化检测时间耗时则很少，且与训练样本数量没有明显关联。总体上，FCM-SBN-CVAPS算法比SVM-CVAPS算法耗时少： FCM-SBN-CVAPS算法的最小耗时约为62 s，最大耗约时为314 s； 而SVM-CVAPS算法最小耗时约60 s，最大耗时约为535 s。值得注意的是，在消耗最少时间的情况下，FCM-SBN-CVAPS算法的Kappa系数为0.78，比SVM-CVAPS算法高0.17； 在消耗最多时间的情况下，FCM-SBN-CVAPS算法的Kappa系数为0.80，比SVM-CVAPS算法高0.13。

2.5 算法性能综合比较

本文采用“变化/非变化”混淆矩阵对FCM-SBN-CVAPS算法、FCM-SBN-PCC算法、SVM-CVAPS算法和SVM-PCC算法的性能进行了综合比较。对比结果如表1所示。

表1 变化检测算法性能比较Tab.1 The performance evaluation of change detection algorithms

1)本文算法无论从总体精度还是Kappa系数都取得了最好的结果，总体精度与Kappa系数比SVM-CVAPS的算法分别高2.33百分点和0.134 1。二者都存在过度估计变化像元的现象，但FCM-SBN-CVAPS算法的错检率低了18.59百分点，表现相对更优。

2)FCM-SBN-CVAPS算法的性能要明显优于FCM-SBN-PCC算法。其总体精度和Kappa系数比FCM-SBN-PCC算法分别高出5.38百分点和0.246 2。且过度估计变化像元的程度明显比FCM-SBN-PCC算法低(错检率低33.68百分点)，表明与PCC模型相比，CVAPS模型不易于受累计分类误差的影响，进一步证明了CVAPS变化检测算法的优越性。

3 结论

本文所提出的FCM-SBN-CVAPS算法针对中低分辨率遥感影像的混合像元问题进行建模，同时使用后验概率向量进行变化检测，有效提高了检测精度和效率。与SVM-CVAPS算法相比，本文算法在总体精度和Kappa系数上都比较理想，此外，算法耗时少，参数设置要求低，不易受过度训练的影响。因此，本文算法具有更高的鲁棒性和实用性。

但类似于许多变化检测算法，FCM-SBN-CVAPS算法生成的初始变化二值图有许多细小的斑块和孔洞，需要进一步的处理，计划未来在模型中引入空间信息以解决这一问题。