GPM卫星降水产品空间降尺度研究——以贵州省为例

杜 懿， 王大洋， 王大刚

(中山大学地理科学与规划学院，广州 510275)

0 引言

近年来，随着计算技术和遥测技术的发展，气象卫星反演已经成为一种新的降水观测途径，国际上也先后涌现出多种卫星降水产品，如GPCP(global precipitation climatology project)，TRMM(tropical rainfall measuring mission)，CMORPH(climate prediction center morphing technique)，PERSIANN(precipitation estimation from remotely sensed information using artificial neural networks)，GSMaP(global satellite mapping of precipitation)，GPM(global precipitation measurement mission)等。由于卫星降水产品能够提供连续的降水时空分布信息，且观测结果受地形和气候条件等的影响较小，可以很好地弥补地面站点观测的不足，目前已被广泛地应用于水文、气象、环境等领域的研究。在诸多无资料地区，卫星反演降水甚至成为区域降水信息获取的唯一手段。然而，受多种因素限制，卫星降水产品的空间分辨率往往不高，如GPCP产品的空间分辨率仅为1.5°×1.5°； CMORPH，PERSIANN和TRMM等产品的空间分辨率也只有0.25°×0.25°； GSMaP和GPM等降水产品的空间分辨率相对较高，达到了0.1°×0.1°，在大尺度区域的研究中总体表现较好，但在小范围区域和小尺度流域的应用中仍然受到诸多限制，其空间分辨率仍有待提高。GPM作为接替TRMM的最新一代卫星降水产品，不仅观测范围更广，时空分辨率也得到了大幅提高，由于搭载了微波成像仪和双频降水雷达，有效提高了对弱降水以及固态降水的探测能力[1]。

目前，常用的降尺度方法主要分为动力降尺度和统计降尺度两大类。其中统计降尺度方法由于计算量小、建模灵活等优点，在国内外得到了广泛应用，是现阶段用来提高卫星降水产品空间分辨率的主要手段[2]。概括来看，基于研究区域的地理、地形等特征而建立的统计降尺度模型在实际应用中效果较好，且理论依据完备。该类降尺度方法的基本假定是目标变量和解释变量之间的相关关系具有空间平稳性，即二者之间的相关关系与空间尺度大小无关。地形指数由于地理稳定性较高，对区域特征的描述性较强，因而常被用作解释变量。

现有研究多以TRMM降水产品为研究对象[3-5]，对新一代卫星降水产品GPM的降尺度研究却所见不多[6]。此外，目前研究中用于建立统计降尺度模型的方法较为单调，多为多元线性回归[7-9]、高次多项式回归[10]和地理加权回归[11-13]等，而具有强大函数逼近能力的机器学习方法却很少被用到，仅有的研究也主要集中在对随机森林回归方法的使用上[14-15]。

鉴于此，本文以2010—2019年的GPM卫星降水数据为研究对象，以地形复杂且气象站点稀少的贵州省为研究区域，以经度、纬度、高程、坡度、坡向等地形因子为解释变量，综合使用多元线性回归模型、地理加权回归模型、极限学习机模型、支持向量机模型以及随机森林回归模型等来进行空间降尺度研究。

1 研究区概况与数据来源

1.1 研究区概况

贵州省地处中国西南内陆腹地，面积达17.61万km2，地理位置介于N24°37′～29°13′，E103°36′～109°35′。地形上，贵州省地处云贵高原东部，境内地势西高东低，从中部向东、南、北三面倾斜，平均海拔在1 100 m左右，全省地貌可分为高原、山地、丘陵和盆地等4种基本类型，其中92.5%的面积为山地和丘陵，平原面积极少。气候上，贵州省属亚热带湿润季风气候，降水丰富，雨热同期，全省多年平均温度为15 ℃左右，多年平均降水量在1 100～1 300 mm之间。贵州省主要气象站点及高程分布如图1所示。

图1 贵州省主要气象站点及高程分布Fig.1 Meteorological stations and elevation distribution in Guizhou Province

1.2 数据来源

根据反演算法的不同，GPM能够提供3种级别的遥感数据产品，其中三级IMERG产品是由校准后的微波所生成的红外降水估计，此外，还融合了地面观测数据，目前已更新至V06B版本。IMERG产品中的 Final Run质量最高，最适合于科学研究，该产品的空间覆盖范围为S60°～N60°，空间分辨率为0.1°×0.1°，时间分辨率为0.5 h。本文使用的数据长度为2010年1月—2019年12月，共10个完整年，120个月份。

数字高程模型(digital elevation model，DEM)是目前用来描述区域地形地貌信息的主要手段。本文所用的DEM数据来自于地理空间数据云(http: //www.gscloud.cn/)提供的GDEMV2 30 m分辨率原始高程数据。

地面气象站点观测数据来自国家气象科学数据中心(http: //data.cma.cn/)发布的《中国地面气候资料月值数据集》。本文选用贵州省区域内的17个站点的2010—2019年间的月降水观测值。贵州省内各气象站点的基本信息如表1所列。

表1 贵州省内气象站点基本信息Tab.1 Meteorological station basic information of Guizhou Province

2 研究方法

本文的具体建模步骤如下[16]：

1)基于30 m DEM数据，以网格为单元，对研究区域内的各个地形因子(高程、坡度、坡向)进行重采样，分别采样成0.1°×0.1°的低分辨率DLR和0.01°×0.01°的高分辨率DHR。

2)基于GPM卫星降水数据，对研究区域内各网格所对应的降水量PLR进行提取，其空间分辨率为0.1°×0.1°。

3)在0.1°×0.1°低分辨率下，建立研究区域内降水量PLR与地形因子DLR之间的映射关系，即

PLR=f(DLR)

(1)

4)以DHR为输入，以f为映射关系，即可得到0.01°×0.01°高分辨率下研究区域内各网格的降水量PHR：

PHR=f(DHR)

(2)

如此，就把降尺度问题转换成了回归问题，研究的关键在于如何找出最适当的映射关系f。回归模型的建模方法众多，本文主要使用了原理简单的多元线性回归、局部信息描述较好的地理加权回归、函数逼近能力优秀的机器学习模型等。

2.1 多元线性回归

多元线性回归原理较为简单，主要是利用统计学方法在多个变量之间建立如下的线性关系：

Y=a0+a1X1+a2X2+…+ak-1Xk-1+akXk

(3)

式中：X为解释变量；Y为目标变量；a为各解释变量所对应的偏回归系数；k为解释变量的个数。已有研究表明[17]，叠加残差后的多元回归模型往往能够表现得更好。

2.2 地理加权回归

地理加权回归是一种局部参数估计方法，相较于多元线性回归，地理加权回归假设解释变量与目标变量之间的关系随空间位置的变化而变化，通过估算研究区内每一位置的目标变量与解释变量之间的参数来建立回归模型，不同于线性回归在整个研究区内通用一套回归参数[18-20]。其原理可用以下公式进行描述：

(4)

式中：n为变量个数；yi为i点处的降水量，i=1,2,…,k； (ui,vi)为i点处的地理坐标；β0(ui,vi)为i点处的常数项回归参数；βj(ui,vi)为第j个变量在i点处的回归参数；ε(ui,vi)为i点处的残差。

2.3 极限学习机

极限学习机是Huang等[21-22]提出的一种单隐含层前馈神经网络。极限学习机的出现有效地解决了前馈神经网络学习速度慢的难题，该算法只需要在网络训练前随机生成输入层和隐含层之间的连接权值和隐含层神经元的阈值，且整个训练过程中无需更新调整。

目前，该模型实现代码已公开发布，下载网址为https: //www.ntu.edu.sg/home/egbhuang/，用户可根据需要免费下载使用。该模型用于回归时，主要优选参数仅有一个，即隐含层的神经元个数。鉴于极限学习机运算效率较快，本文直接使用遍历法来优选参数。

2.4 支持向量机

支持向量机是由Vapnik等[23]在统计学习理论的基础上提出的一种新的机器学习方法，其在很大程度上解决了过学习、非线性和维数灾等问题，为小样本机器学习问题建立了一个较好的理论框架[23-24]。

本文基于LIBSVM V3.24开源工具箱来进行支持向量机的建模工作，该工具箱所涉及的参数调节较少，提供了很多默认参数。一般情况下，当采用RBF函数作为核函数时，需要优化的参数主要有惩罚系数c和RBF核函数的自带参数g，LIBSVM V3.24工具箱内嵌了交叉验证法来对参数c和g进行优选，但是考虑到epsilon-SVR模式中损失函数值p对模型的最终表现也有较大影响，故也将此参数作为待优选参数。由于遗传算法具有强大且高效的全局优化能力，本文以其来对c，g，p等参数进行寻优。

2.5 随机森林回归

随机森林是由Breiman[25]提出的一种基于决策树的机器学习模型，与神经网络算法相比，其计算量小且精度较高。该算法目前在多种环境下均可实现，如MATLAB，Python和R等，其中对模型结果影响较大的参数主要有决策树数目ntree(默认值为500)和指定节点中用于二叉树的变量个数mtry(默认值为输入变量个数的二次方根或三分之一)。一般情况下，mtry的取值对模型效果影响不大，需要进行优选的参数就只有ntree。由于随机森林模型也有极快的计算效率，故本文直接对ntree进行遍历寻优。

2.6 评价指标

本文选用的评价指标主要包括有平均绝对误差(mean absolute error，MAE)、平均绝对百分比误差(mean absolute percentage error，MAPE)、均方根误差(root mean square error，RMSE)以及皮尔逊相关系数R，前3个指标用来表征模型的模拟误差，后一个指标用来描述空间一致性。各评价指标的计算公式如下所示：

(5)

(6)

(7)

(8)

3 研究结果

3.1 多年平均尺度

对2010—2019年间贵州省的多年平均、多年季节平均等时间尺度的降水量分别建立基于多元线性回归、地理加权回归、极限学习机、支持向量机、随机森林回归等降尺度模型，并将各情景下的降尺度前、后的降水量与相应的实测站点的降水量进行比较。

基于研究区域范围，在0.1°×0.1°分辨率下共提取出1 991组有效样本，每组样本的输入变量包括有网格的经度、纬度、高程、坡度、坡向等5个地形因子，输出变量则为网格在指定时间尺度下的GPM降水量。在建立多元线性回归模型和地理加权回归模型时，以全部1 991组样本计算模型，再利用该模型对新的输入样本进行模拟，最终得到0.01°×0.01°分辨率下的GPM降尺度结果。而在机器学习模型的建模过程中，通常需要先对模型的可行性进行验证，进而才能对新的输入样本进行模拟。根据经验，按照4∶1的原则进行样本划分，各时间尺度下的机器学习模型在建模时均取前1 600组样本组成训练集，剩余391组样本组成验证集。模型有效性以MAPE指标来进行评价，一般当MAPE≤20%时，说明模型表现较好，可以实际应用。

表2为3种机器学习模型MAPE结果，可以看出，除随机森林回归模型在多年冬季的验证期内模拟误差过大，其余各机器学习模型在各时间尺度下均建模成功，且模拟精度较高。

表2 机器学习模型的MAPE计算结果Tab.2 The MAPE of machine learning models (%)

表3—7给出各降尺度模型在多年平均、多年季节时间尺度下的降尺度效果评价，其中0.1°×0.1°分辨率表示降尺度前的GPM数据，0.01°×0.01°分辨率表示降尺度后的GPM数据。

表3 各时间尺度下多元线性回归模型评价指标计算结果Tab.3 The results of multiple linear regression models under various time scales

表4 各时间尺度下地理加权回归模型评价指标计算结果Tab.4 The results of geographical weighted regression models under various time scales

表5 各时间尺度下极限学习机模型评价指标计算结果Tab.5 The results of extreme learning machine models under various time scales

(续表)

表6 各时间尺度下支持向量机模型评价指标计算结果Tab.6 The results of support vector machine models under various time scales

表7 各时间尺度下随机森林回归模型评价指标计算结果Tab.7 The results of random forest regression models under various time scales

1)多元线性回归模型。相较于降尺度前，降尺度后的结果不仅空间分辨率有了极大提高，观测精度也有较大提升。在多年平均和多年季节时间尺度下，降尺度后的高分辨率数据不仅误差减小明显，与站点实测数据的相关性也有了明显提高。在多年冬季时间尺度上，降尺度后的高分辨率数据与站点实测数据的相关性虽然没有提高，但基本稳定。

2)地理加权回归模型。从观测误差上来看，除了多年春季时间尺度基本保持不变，其余4种时间尺度下的观测误差均有明显减小。从与站点实测数据的相关性上来看，相较于多元线性回归模型，地理加权回归模型在全部时间尺度下的相关性均表现出明显的提高。

3)极限学习机模型。基于极限学习机的降尺度模型也基本表现不错，但相较于多元线性回归和地理加权回归模型仍有一定差距。多年平均和多年夏季时间尺度下，降尺度后的数据无论是观测精度还是与站点实测降水的相关性，均有所提升； 多年春季时间尺度下，虽然观测精度有所提高，但相关性有所减小； 多年秋季和多年冬季时间尺度下，不仅观测精度有所下降，与站点实测数据的相关性也有所减小。

4)支持向量机模型。基于支持向量机的降尺度模型整体表现较好，要优于极限学习机模型。在多年夏季和多年秋季时间尺度下，降尺度后的数据在精度和相关性上均有明显提升； 多年平均和多年冬季时间尺度下，降尺度后的数据在观测精度上有较大的提高，但与站点实测数据的相关性却有所减小； 多年春季时间尺度下，降尺度后的数据在观测精度和相关性两方面均存在微弱下降。

5)随机森林回归模型。基于随机森林回归的降尺度模型表现不大理想。在多年夏季时间尺度下，降尺度后的数据在观测精度和相关性上均有明显提高； 在多年平均、多年春季时间尺度下，虽然观测精度有一定程度的提高，但与站点实测数据的相关性却有所减弱； 多年秋季和多年冬季时间尺度下，不仅观测误差上升，与站点实测数据的相关性也明显减小，尤其是多年冬季时间尺度的表现最差。造成这一结果的原因是在建模过程中模型未通过可行性检验，导致模型失效。

综合比较以上5种降尺度模型，可以发现多元线性回归模型、地理加权回归模型、极限学习机模型、支持向量机模型表现较好。进一步对比发现，多元线性回归模型和地理加权回归模型的降尺度效果整体上还是要优于极限学习机模型和支持向量机模型，可能的原因是在建模过程中前两个模型利用了全部样本信息(1 991组)，而后两种机器学习模型由于需要额外划出一部分样本来验证模型的可行性，造成了学习样本数(1 600组)减少，样本学习信息不足，进而影响了降尺度结果。整体来看，多元线性回归模型原理最为简单、计算最为方便、效果也最为稳定。

图2—6为多元线性回归模型在多年平均和多年各季时间尺度下的降尺度前、后效果对比。

(a) 降尺度前 (b) 降尺度后图2 多年平均年降水量空间分布Fig.2 Spatial distribution of average annual precipitation

(a) 降尺度前 (b) 降尺度后图3 多年平均春季降水量Fig.3 Spatial distribution of average spring precipitation

(a) 降尺度前 (b) 降尺度后图4 多年平均夏季降水量Fig.4 Spatial distribution of average summer precipitation

(a) 降尺度前 (b) 降尺度后图5 多年平均秋季降水量Fig.5 Spatial distribution of average autumn precipitation

(a) 降尺度前 (b) 降尺度后图6 多年平均冬季降水量Fig.6 Spatial distribution of average winter precipitation

图7 研究区逐年降水量变化过程Fig.7 The change process of precipitation in the Guizhou Province from 2010 to 2019

3.2 年尺度

本文使用的GPM降水数据的时间范围为2010年到2019年，采用算术平均法来计算研究区域的面平均降水量。图7为研究区域在2010—2019年期间的逐年降水量变化过程。可以明显看出，2011年为典型干旱年，2014年为典型湿润年。

采用多元线性回归模型分别对干、湿典型年的年降水量进行空间降尺度研究。表8为基于多元线性回归模型的降尺度结果评价。

表8 干、湿典型年降水量降尺度效果评价Tab.8 Evaluation of downscaling results of typical annual precipitation of dry and wet

由表8可见，基于多元线性回归的降尺度模型在干、湿典型年中均表现较好。降尺度后的GPM数据，无论是在观测精度上还是在与站点实测数据的相关性上，均得到了不同程度的提高。此外，相较于典型干旱年，典型湿润年的降尺度效果更优。

图8—9为研究区域内典型干、湿年降尺度前、后的年降水量空间分布情况。

(a) 降尺度前 (b) 降尺度后图8 典型干旱年年降水量Fig.8 Annual precipitation in a typical drought year

(a) 降尺度前 (b) 降尺度后图9 典型湿润年年降水量Fig.9 Annual precipitation in a typical wet year

3.3 月尺度

为了进一步验证多元线性回归降尺度模型在月尺度上的应用效果，分别对研究区域典型干、湿年的月降水量进行降尺度处理。并通过观察降尺度前后降水的年内分配情况来检验模型的表现效果，结果如图10和图11所示。

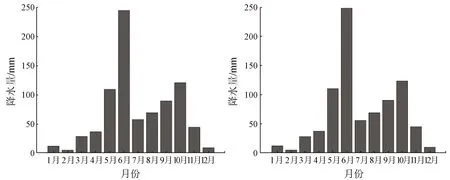
(a) 降尺度前 (b) 降尺度后图10 典型干旱年降水量月程分配Fig.10 Monthly distribution of precipitation in a typical dry year

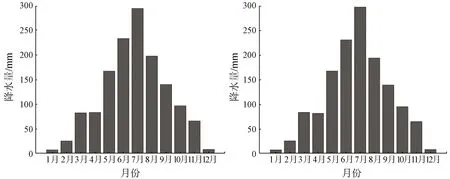
(a) 降尺度前 (b) 降尺度后图11 典型湿润年降水量月程分配Fig.11 Monthly distribution of precipitation in a typical wet year

从图10和图11中可以看出，两种典型年下，降尺度后的月降水量无论是在量值上还是在月程分配上均和降尺度前保持了较高的一致性，可以充分地说明基于多元线性回归的降尺度模型在贵州省区域有着相当好的适用性与可靠性。

4 结论

本文以2010—2019年贵州省区域的GPM卫星降水数据为研究对象，借助经度、纬度、高程、坡度和坡向等地形因子来建立空间降尺度模型，主要取得以下结论：

1)在多年时间尺度的降尺度研究中，多元线性回归、地理加权回归、极限学习机、支持向量机等模型均表现较好，其中以多元线性回归模型表现最好。鉴于多元线性回归模型原理简单、建模方便，且在所有模型中对观测精度的提高最为明显，故将其选为贵州省区域GPM卫星降水数据的最佳空间降尺度模型。

2)基于多元线性回归模型，分别对研究区典型干、湿年的年降水量进行降尺度研究，相较于降尺度前，降尺度后的降水数据除了具有更高的分辨率外，还具有更高的观测精度以及更好的相关性。典型干旱年下，平均绝对百分比误差从11.62%下降到了11.23%，与站点实测数据的相关系数从0.72上升到了0.73； 典型湿润年下，平均绝对百分比误差从11.22%下降到了10.71%，与站点实测数据的相关系数从0.50上升到了0.62。

3)为了进一步检验多元线性回归降尺度模型在月时间尺度上的应用效果，分别对典型干、湿年的月降水量进行了降尺度处理，效果仍然令人满意。在提高降水数据空间分辨率的同时，无论是在量值上还是在月程分配上，均保持着较高的一致性。

机器学习模型在本次研究中的表现并未优于多元线性回归模型和地理加权回归模型，可能的原因是研究区域较小，可利用样本数较少，模型无法得到充分的训练，导致学习能力有限。随着研究区域的扩大、样本数的增多，在经过大数据训练后的机器学习模型相信能获得更好的降尺度效果。

本文在建立降尺度模型的过程中仅使用了地形因子变量，虽然在各个时间尺度上均能得到较好的应用效果，但并不表明没有进一步提升的空间，如引入植被指数、地表温度、土壤含水量等变量对降尺度效果是否会有改进，仍需要继续开展研究。