冲击环境下航天器电磁自锁阀锁闭特性研究*

鞠震昊 闫寒 尤罡 张文明†

（1.上海交通大学机械系统与振动国家重点实验室，上海 200240）（2.上海空间推进研究所，上海 201112）

引言

运载火箭飞行过程中，航天器要经历复杂和严酷的振动力学环境［1，2］.冲击环境是航天器飞行时常见的力学环境，发动机点火、星箭分离、火工品起爆等都会产生冲击载荷［3］，过量的冲击载荷可能导致航天器中关键部件性能的下降甚至是失效.因此，航天器关键部件的抗冲击性能研究一直是研究人员关注的重点课题［4，5］.

电磁自锁阀是液体火箭发动机中广泛使用的一种控制阀门，通常安装在推进剂管路中，在电信号的控制下打开或关闭，从而控制发动机的点火和运行［6］.电磁自锁阀结构紧凑、响应速度快、具有两个稳态位置.然而，当电磁自锁阀受到沿阀芯运动方向的强冲击载荷影响时，阀芯可能会从一个稳态位置移动至另一个稳态位置，发生误动作，从而影响航天发动机的正常运行，严重时可能造成重大飞行事故.比如，2018年某航天器飞行过程中，发动机入口压力异常增高，经排查发现，该管路中的电磁自锁阀受到器箭分离过程的强冲击载荷影响，发生了异常打开，所幸处理及时，未造成严重后果.

近年来，研究人员重点关注冲击载荷下航天器结构与有效载荷的强度问题，分析冲击敏感的元器件和脆性材料是否会在冲击载荷的作用下发生损伤或破坏［7，8］，对冲击载荷作用下自锁阀阀芯的动力学特性及锁闭性能研究较少.

陈其法［9］等针对运载火箭安全阀的一定载荷下的颤振导致阀门损坏的现象，基于流固耦合方法阐述了相关机理并提出了有效的改进措施.王春民等［6］研究了一种气体自锁阀在振动和冲击力学环境下的工作特性，讨论了不同力学条件对自锁阀工作过程的影响，研究表明自锁阀受导阀控制气压力、随机振动量级和冲击方向的影响较大.然而，该研究中将自锁阀假设为刚性结构，没有考虑冲击载荷在自锁阀中的传递，难以准确判断电磁自锁阀在一定冲击载荷下阀芯的开闭状态.

针对电磁自锁阀在冲击环境下的锁闭性能问题，本文建立自锁阀阀体-阀芯动力学模型，利用有限元方法研究冲击载荷在自锁阀阀体中的传递特性，根据理论给定标准及上下界响应谱曲线，进行冲击响应分析，基于能量法判断自锁阀的锁闭特性，提出自锁阀抗冲击裕度分析方法，并通过冲击试验验证该分析方法的正确性，为后续型号自锁阀的设计、试验提供理论基础和技术支撑.

1 模型建立

1.1 工作原理及锁闭失效

本文所研究的电磁自锁阀如图1所示，通过设计双磁路结构，在两个间隙处均产生吸力，且小间隙处吸力大于大间隙处，使阀芯保持在小间隙位置.当需要动作时，发出控制信号使线圈通电，抵消小间隙处的磁通，同时增加大间隙处的磁通，使大间隙处的吸力大于小间隙处，使阀芯移动至大间隙处.根据电磁自锁阀的自锁和动作原理可知，正常情况下阀芯在磁场的作用下位于小间隙处，只有当施加控制信号时才会移动至大间隙.自锁阀通过连接工装安装在航天器上，当航天器受到器箭分离、火工品爆炸等引起的冲击载荷时，载荷从工装底板传递至自锁阀，使自锁阀产生冲击响应.阀芯在小间隙处与自锁阀阀体存在接触，也受到冲击载荷的影响，当冲击载荷过大时，阀芯可能克服小间隙处的吸引力，误动作至大间隙处，从而导致管路的异常打开或关闭.

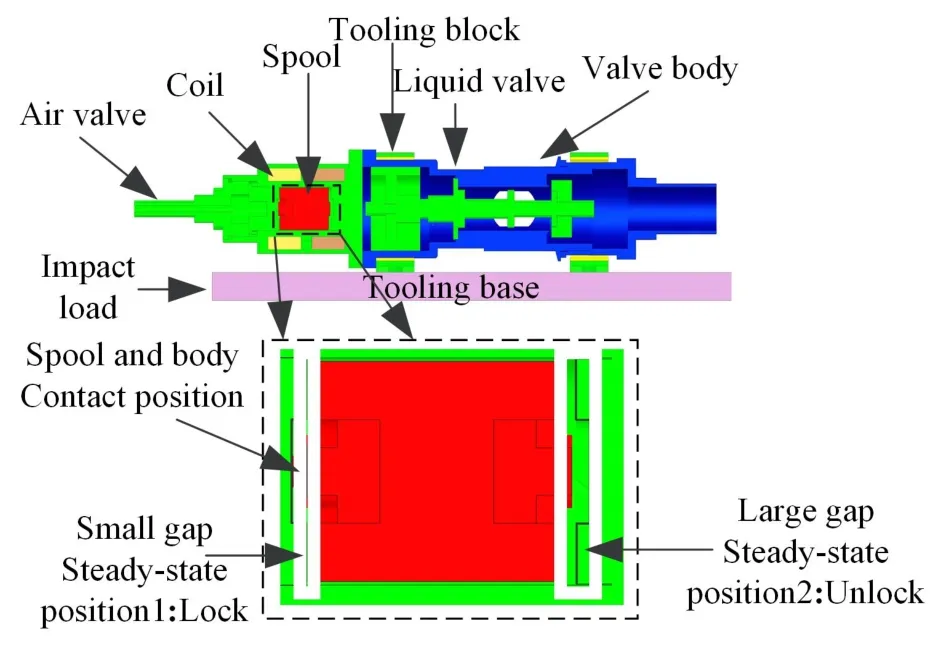
图1 自锁阀示意图Fig.1 Schematic diagram of self-locking valve

自锁阀产品装配前，用与产品磁路结构完全相同的试验衔铁和试验阀座进行磁力测试.将试验衔铁放入自锁阀线圈组件内，行程调至规范值.在室温条件下，接通外接电源调节至额定电压.通过砝码称重法，测量对应开位、关位两种状态下的锁闭力与电磁力.以阀芯在小间隙处的稳态位置作为原点，无源状态下阀芯受到的磁场力与位移的关系如图2（a）所示，磁场力的正方向指向小间隙处，负方向指向大间隙处.可以发现，磁场力在小间隙处最大，达45.5 N，随着阀芯向大间隙处移动，指向小间隙的磁场力逐渐降低；越过磁场力为0的不稳定平衡点之后，阀芯受到指向大间隙的磁场力逐渐增大.并且，通过一次多项式拟合磁场力，确定系数R2=0.992，说明磁场力与阀芯位移近似满足线性关系，可以将磁场力等效为具有负刚度的弹簧.根据拟合得到的磁场力，以小间隙处为零势能位置，计算阀芯具有的磁场势能，如图2（b）所示.

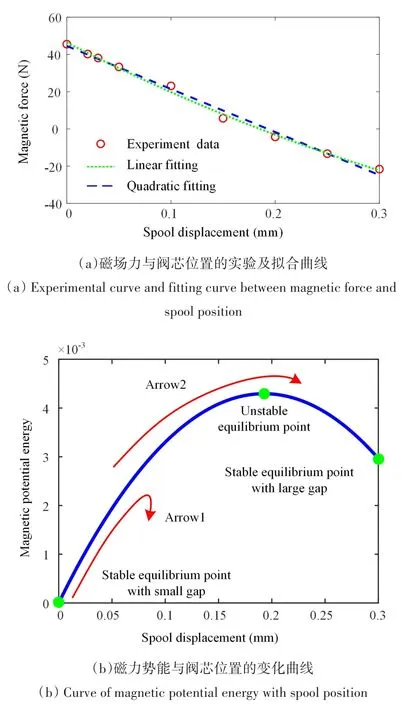
图2 磁场力、磁场势能与阀芯位置变化曲线Fig.2 The relationship between magnetic field force，magnetic field potential energy and spool position

根据阀芯受到的磁场力和磁场势能，可以分析阀芯在冲击载荷作用下的锁闭失效机理：自锁阀-工装结构受到冲击载荷，阀体产生持续时间很短的冲击响应速度，考虑到阀芯在小间隙处与阀体接触，受到阀体传递而来的速度，从而具有一定的初速度.如果阀芯初速度较小，阀芯的动能不能克服磁场势能从而越过不稳定平衡点，则阀芯依然会保持自锁，如图2（b）中的箭头1所示；反之，如果阀芯初速度较大，能够越过不稳定平衡点，则阀芯移动到大间隙处，自锁阀锁闭失效，如图2（b）中的箭头2所示.因此，判断自锁阀是否发生锁闭失效的关键，在于计算阀芯与自锁阀接触位置的冲击响应速度.

自锁阀由多种零件组成，并通过螺栓连接在工装上，结构较为复杂，难以通过解析方式得到冲击载荷作用下的响应速度.因此，建立工装-自锁阀结构的有限元模型，针对该模型进行冲击响应分析，计算得到阀体与阀芯接触位置的响应速度，从而判断自锁阀的锁闭状态.

1.2 有限元建模

根据图1所示的工装-自锁阀结构，建立对应的有限元模型.该模型主要由自锁阀与冲击试验工装两部分组成的，其中工装由工装底板，工装卡块和橡胶垫组成，自锁阀结构主要包括线圈、主阀体、从阀体、阀芯、线圈等部件［10］.自锁阀通过连接螺栓压紧在试验工装上，试验工装通过螺栓连接固定在冲击试验台面上.模型主要组成部分设计材料清单如表1所示.

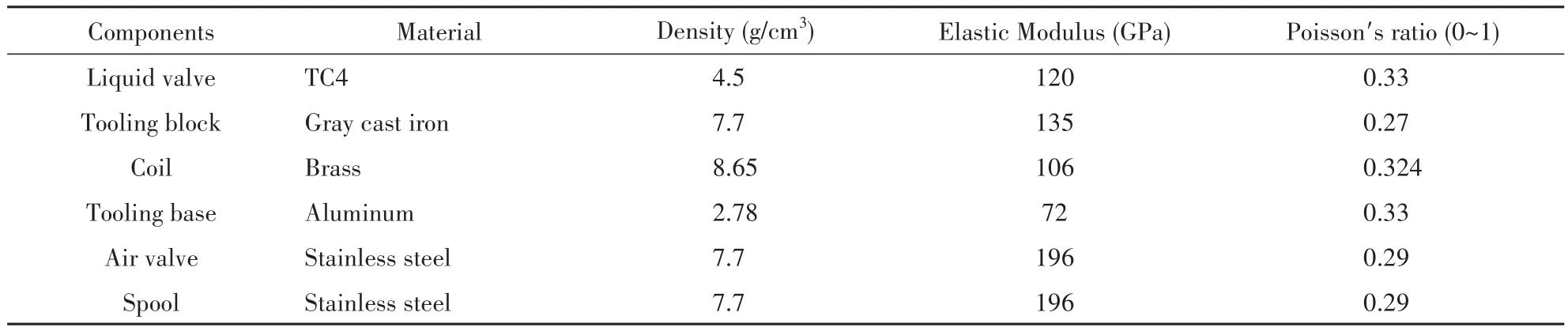
表1 有限元模型各部件材料参数Table 1 Material parameters of finite element model

采用ABAQUS有限元分析软件进行工装-自锁阀的冲击响应分析.考虑到试验工装整体结构比较简单，采用C3D8R六面体网格进行划分，其中，将2对压块中的2个下压块与试验工装的底板采用共节点方式划分网格.对于自锁阀体，考虑到其结构较为复杂，针对不同部件采取不同划分方式.对于铜线圈、橡胶垫等较为规则的零部件划分六面体网格，对于阀体等不规则部件则划分四面体网格.使用六面体单元时，注意坍塌率等较为敏感的网格质量参数，使用四面体网格时，重点关注最小最大角等较为敏感的网格质量参数，并注意整体和局部加密网格.

冲击试验中，上下工装压块为螺栓连接，考虑到上下压块连接刚性较大，且该部分不是整个结构的关键区域，对结构的模态影响较小，因此采用Coupling连接方式分别耦合两对压块的内侧全部节点.对于自锁阀阀体中的零部件，根据实际装配关系，采用Tie连接进行约束.液路阀与气路阀之间通过螺栓连接，这里简化为刚性连接，使用Coupling连接方式分别耦合4对孔内侧面.

在冲击试验中，试验工装通过底板的4个通孔与工作台面螺纹连接，固定于冲击试验台上，其连接方式可以视为刚性连接.因此，约束试验工装底板的4个通孔内侧面所有节点的全部自由度，完成边界条件设置.最终得到的工装-自锁阀结构有限元模型如图3所示.

图3 工装-自锁阀有限元模型示意图Fig.3 Schematic diagram of tooling-self-locking valve finite element model

1.3 冲击响应分析

结构在冲击载荷作用下的响应是一个瞬态过程，然而，冲击载荷的时域曲线往往变化很大，并且对复杂结构进行瞬态分析需要耗费大量计算资源.因此在实际应用中，通常基于冲击响应谱计算结构在冲击载荷作用下的响应情况.

冲击响应谱是一系列不同固有频率的单自由度系统对于同一冲击激励的最大响应包络谱图［11］，其计算过程如下：将某一冲击载荷施加于一系列线性、单自由度弹簧-质量系统，以单自由度系统的固有频率作为自变量，以各系统在冲击载荷作用下的响应最大值作为因变量，绘制成曲线，该曲线即冲击载荷所对应的冲击响应谱［12］.冲击响应谱有多种数值计算方法，如龙格库塔法、数字滤波法、样条曲线法等［4］.以冲击响应谱作为激励，可以利用模态参与系数计算结构响应的极值.第α阶模态在s方向的模态参与系数ηαs可以表示为：

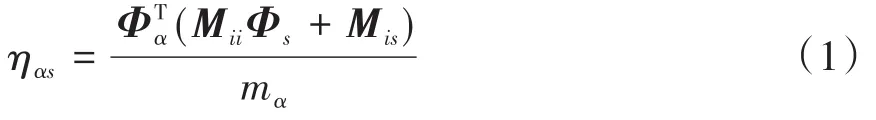
式中Φγ为正则模态，Φs为约束模态，Mii、Mis为分解的模态质量矩阵，mα为模态质量.设qα为表示冲击响应谱在第α个固有频率处的值，则冲击载荷引起的模态最大值可以表示为：

式中，Rmaxα为模态坐标系中第α阶模态在冲击载荷下的响应最大值，j=1-6表示运动方向，包括三个平动方向和三个转动方向，tj为j方向的方向余弦.

利用模态向量矩阵进行坐标变换，可以得到结构第α阶模态的实际最大响应值：

考虑到每阶模态产生最大响应值的时间并不相同，因此需要采用合适的模态合成方法对结构各阶模态阶进行组合，常用的模态合成方法有绝对值求和法（ABS）、平方和的平方根法（SRSS）等.其中，绝对值求和法是将各阶模态最大响应值的绝对值直接相加：

绝对值求和法假设所有模态响应的最大值发生在同一时刻，是最保守的一种模态叠加法，得到的结果通常远高于实际响应值.SRSS方法的计算过程如下：

2 模态分析与试验验证

模态分析是结构动力学分析的基础，也是利用模态叠加理论进行冲击响应分析的前提.工装-自锁阀结构的自由振动方程为：

式中，M、C、K分别为结构的质量矩阵、阻尼矩阵和刚度矩阵，U为位移向量.上式的特征方程可写为：

式中，ω为系统的固有频率，Φ为模态振型向量.计算上式，可以得到结构固有频率f和模态振型，如图4所示.为了验证有限元模型和模态分析的正确性，使用LMS Test.Lab振动噪声测试分析系统，对工装-自锁阀结构进行锤击试验，如图5所示.通过测量结构的频响函数得到该结构的固有频率，并与有限元仿真得到的结果进行比较，如表2所示.由于实际安装与装配过程中，工装与自锁阀的连接方式以及自锁阀内部各部件间的装配关系并非完全如仿真模型中理想化考虑的tie连接固定，实验固有频率与仿真固有频率之间存在一定误差.根据表2可知，固有频率的仿真结果与试验结果的偏差基本在5%以内，说明了有限元模型和模态分析的正确性，从而保证基于模态叠加原理的冲击响应分析的正确性.

图4 工装-自锁阀前四阶固有频率与振型Fig.4 Tooling-self-locking valve natural frequency and vibration mode between the first and fourth order

图5 模态试验示意图Fig.5 Schematic diagram of modal test

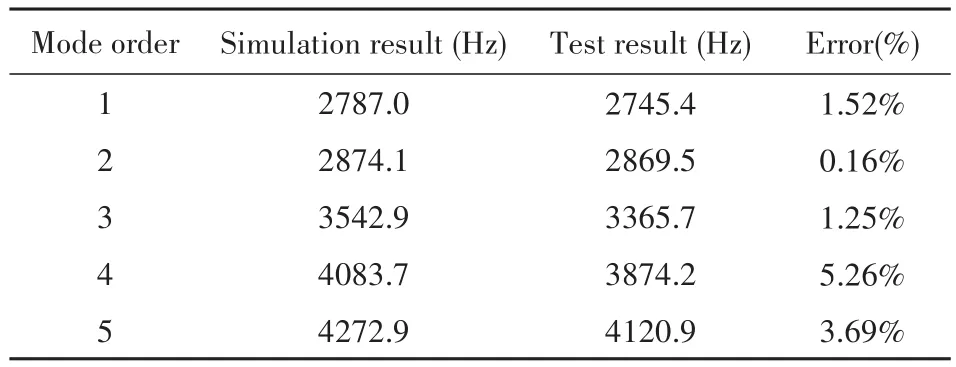
表2 固有频率的试验结果与仿真结果Table 2 Natural frequency test results and simulation results

3 阀芯锁闭状态分析

根据建立的工装-自锁阀有限元模型，在给定的响应谱下进行冲击响应分析，得到阀芯最大初速度，通过能量法判断阀芯的自锁状态.冲击试验条件如图6所示，在100～800Hz的频率范围，响应谱的斜率为+6dB/oct，在800～4000Hz的范围，响应谱幅值为1000g.并且，由于冲击载荷本身的不确定性，响应谱容差为：频率≤3000Hz，±6dB；＞3000Hz，+9.0dB～-6.0dB.根据给定的冲击响应谱，对工装-自锁阀结构进行冲击响应分析，得到阀体与阀芯接触位置的最大响应速度.根据该响应速度计算阀芯动能，如果动能小于阀芯的磁场势能，则阀芯保持自锁；如果动能大于磁场势能，则阀芯异常开启.

为了研究自锁阀阀芯冲击裕度，以图6所示的理论标准响应谱、理论响应谱最大值、理论响应谱最小值作为激励，进行冲击响应分析，得到阀芯与阀体接触位置的最大响应速度如图7所示.

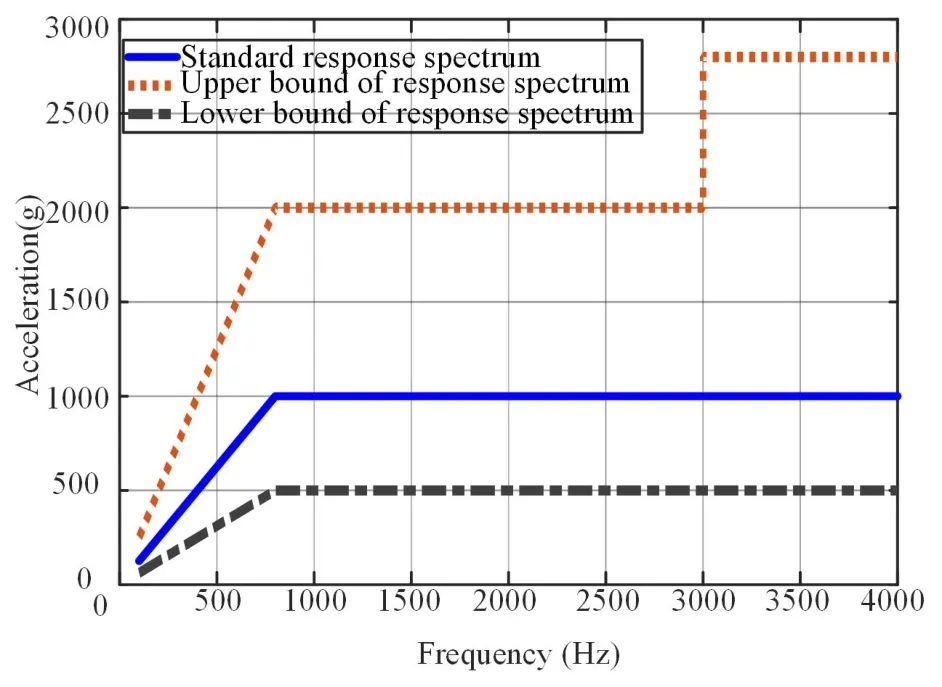
图6 冲击响应谱曲线Fig.6 Shock response spectrum curve

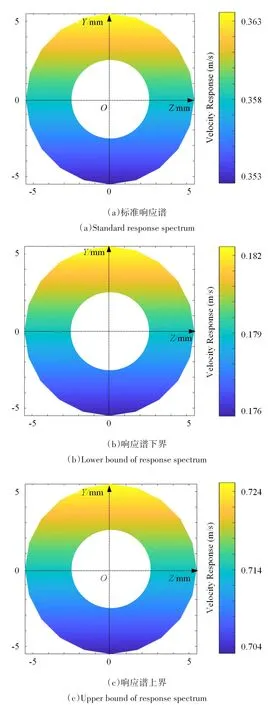
图7 冲击响应谱作用下阀芯与阀体接触位置响应速度云图Fig.7 Self-locking valve impact test

根据速度响应云图可知，由于自锁阀自身的弹性，阀芯-阀体接触面的响应速度与位置有关，但变化不大，可以使用端面的平均速度作为阀芯最大速度.根据冲击响应分析结果，阀芯在以上三种理想工况下的锁闭状态如表3所示.根据结果可知，按照给定的冲击响应谱以及容差范围，自锁阀存在锁闭失效的可能.为了提高抗冲击裕度，需要满足最大理论响应谱冲击载荷下阀芯动能大于磁场势能的条件，从而保证在冲击试验给定容差下阀芯的抗冲击锁闭性.

表3 阀芯锁闭状态Table 3 Spool locked state

航天器振动试验是航天器卫星环境工程的重要组成部分.为保证其飞行可靠性，航天器均要进行地面试验以考核其对力学环境的适应性［13］.冲击试验作为一类重要特殊环境下振动试验，对考核自锁阀阀芯能否经受太空中强冲击恶劣动力学环境起着非常重要的作用.

为了验证阀芯锁闭状态分析结果的正确性，开展自锁阀的冲击试验，如图8所示.将自锁阀-工装固定在摆锤式冲击台的台面上，给定冲击响应谱，并设定容差范围.调整摆锤角度进行冲击试验，在冲击台控制系统中获得反馈生成的响应谱结果.试验结束后，查看自锁阀开闭与否，如果开启则说明锁闭失效.以试验得到的实际冲击响应谱作为输入，分析自锁阀的冲击响应并计算阀芯动能，利用能量法判断阀芯开闭情况，与试验结果进行对比.

图8 自锁阀冲击试验实物图Fig.8 Self-locking valve impact test

进行四次冲击响应试验，测得的响应谱如图9所示.以这些响应谱作为冲击响应分析的输入载荷，得到阀芯初速度，计算阀芯动能并与磁场势能对比从而判断阀芯锁闭状态，并将其与试验结果进行对比，发现理论分析结果与试验结果一致，如表4所示，说明结合冲击响应与能量法能够准确判断自锁阀锁闭状态.

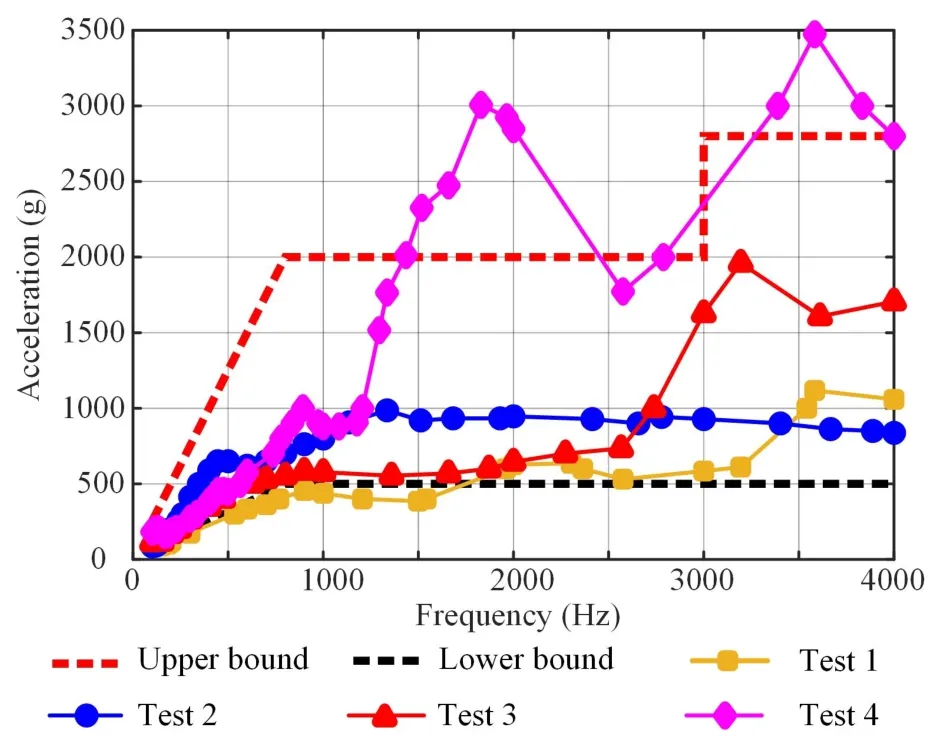
图9 冲击试验响应谱Fig.9 Impact test response spectrum

表4 阀芯开闭状态理论结果与试验结果对比Table 4 Comparison of theoretical and experimental results of valve core opening and closing state

4 总结

电磁自锁阀具有结构紧凑、响应速度快等优点，是液体火箭发动机中广泛使用的控制阀门.在航天器受到火工品爆炸、器件分离等引起的冲击载荷时，电磁自锁阀可能发生锁闭失效，引起发动机故障.因此，需要对电磁自锁阀在冲击环境下的锁闭状态进行有效评估.针对这一问题，本文从能量角度研究了自锁阀的锁闭失效机理，建立了工装-自锁阀有限元模型，并利用模态试验验证模型的正确性.使用工装-自锁阀有限元模型，研究自锁阀的冲击响应，并结合阀芯能量分析，判断阀芯锁闭状态.为了验证理论分析的正确性，利用摆锤式冲击台开展冲击响应试验，以冲击试验的实际响应谱作为激励，分析阀芯锁闭情况，将所得理论结果与试验结果进行对比，二者完全一致，验证了阀芯锁闭分析方法的有效性.本文的研究能够为后续型号电磁自锁阀的设计、试验提供理论基础和技术支持.