文山都龙矿区不同规模矿体可采系数的测定研究
2022-01-06杨涛
杨涛
(云南华联锌铟股份有限公司,云南 文山 663700)
1 矿区矿体特征
文山都龙矿区矿体走向近南北,倾向西,倾角10°~40°,局部倾角可达60°,锌锡矿体绝大多数为盲矿体,并以10°~15°的侧伏角自北而南侧伏。矿体沿层产出,部分矿体与含矿层有一定交角,在平面图上呈南北向展布,剖面上呈多层出现,显示叠瓦状排列特征(如图1 所示)。
矿体产状随含矿层同步褶曲,沿走向和倾向均具波状起伏。矿段东部的矿体产状平缓,部分矿体倾角趋近水平;西部的矿体倾角稍陡,一般倾角10°~40°,深部矿体局部倾角可达60°。矿体外形不太规则,具分枝复合、膨胀收缩等变化。大矿体一般为似层状,小矿体多呈透镜状、扁豆体、囊状。厚大矿体中有夹石存在,往往有大理岩、片岩残留体,其形态很不规则,呈扁豆状或囊状(如图2 所示)。

图2 文山都龙矿区矿体呈不规则形态产出
2 可采系数测算方法
可采系数是指可采资源量占地质资源量的比例,是地质资源量换算成可采资源量的关键参数。研究可采系数,其实就是研究可采资源,因为地质资源量的基数已经为固定值。通过查阅大量文献资料,均未发现有关于露天多金属矿山可采系数的技术方法,而关于可采系数的矿产资源研究更多是在页岩气资源、煤层资源、油砂资源方面。例如煤层气可采资源量计算的主要方法有体积法、类比法、数值模拟法和产量递减法。这些计算方法需要参考的影响因素较多,基本每个因素都是需要大量的数据去分析论证,一旦某个因素的数据信息难以收集或资料不全将难以开展测算评估工作。
文山都龙矿区的地质特征较为复杂,矿山剥离开采工作也较为精细复杂,精细的生产工作一定程度上也会将可采系数影响因子进行分解,这也给影响因子数据收集带来较多工作量或技术难题,影响因子数据收集的不全面性,将直接导致可采系数测算结果的可靠性降低。为保证可采系数测算结果的可靠性,就必须优化测算方法,可以利用“间接法”来推算出可采系数,这样便可避开收集影响可采系数因素的数据收集工作,即:用初始数据及结果数据,推算过程参数(可采系数)。这里通过流程图的方式,将可采系数测算方法优选过程进行展示(如图3 所示)。
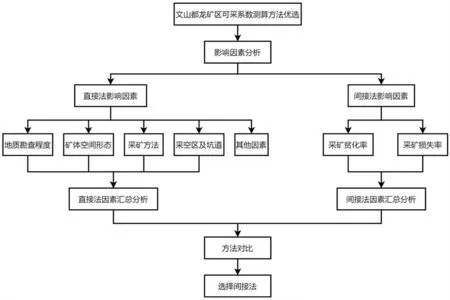
图3 文山都龙矿区矿体可采系数测算方法优选流程
3 确定计算公式
由于我国不同地区的矿床成矿条件、矿体特征以及开采条件等方面存在明显差异,因此,具有不同的可采系数。研究可采系数,就必须确定可采系数的计算公式。按照定义,可采系数的计算见式(1)。

式中:Q采——可采资源量;Q地——地质资源量。
通过式(1)可以看出:要研究可采系数,实际就是要研究可采资源量。因为地质资源量可以依据地质资料确定其具体数据,而可采资源量则受到矿体的空间形态、采矿设计方法、采空区及坑道等因素的影响。结合文山都龙矿区实际情况,因矿山属于露天开采,设计范围内的所有矿石均会被剥离开采,故文山都龙矿区的可采资源量数据可以通过实际采出矿石量套贫化损失率反算后,再减去因矿体在开采过程中形态改变变化量而得出,计算公式见式(2)。

式中:Q实——实际采出矿石量;γ——矿石贫化率;ρ——矿石损失率;Q变——改圈改算矿石增减量。
故可采系数的最终计算见式(3)。

4 不同规模矿体贫化损失率计算
确定了可采系数的计算公式后,则需要对公式中的对应数据进行数据收集,保证收集数据的真实证、合理性是该研究过程中的重要步骤。因此需要对数据进行分析处理,选取具有代表性数据。结合矿山实际情况,矿体厚度越小贫化率越大,贫化率与目前采场开采地质因素、现状设备配置较一致,同时部分矿体受矿体形态、赋存位置、矿石内部结构复杂性影响,导致贫化损失率会受到矿体厚度规模的影响。这里暂且定义矿体厚度小于3m 的矿体为薄小矿体,矿体厚度3~5m 的矿体为中厚矿体,矿体厚度大于5m 的矿体为厚大矿体。该次收集的数据为2021 年4—9 月的生产数据,主要为采矿贫化率(见表1)、损失率(见表2)、月计划范围内的地质资源量及计划范围内实际采出矿石量。

表1 2021 年4—9 月贫化率测算结果
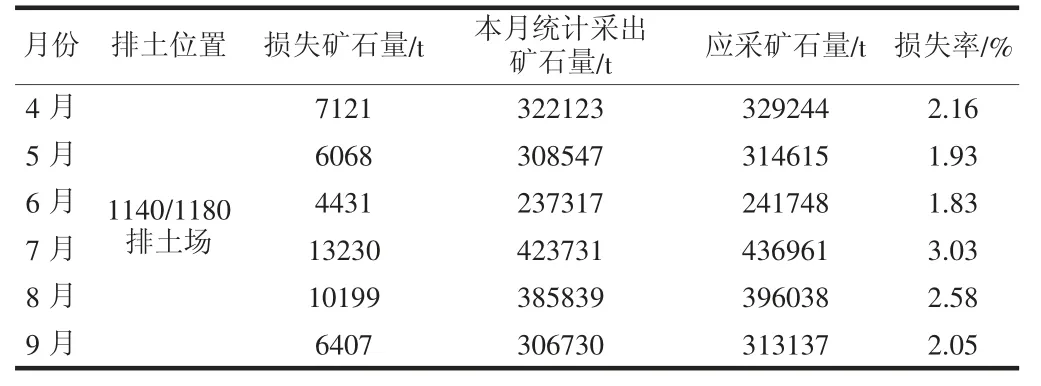
表2 2021 年4—9 月损失率测算结果
矿山贫化损失率的测定工作一般采用直接法及间接法。结合文山都龙矿区的生产实际,由于文山都龙矿区的矿体形态、品位变化较大,地质条件较为复杂,因此在计算贫化率时使用了直接法,对不同规模的矿体进行贫化率测定。而在计算损失率时,通过直接法进行计算工作量较大,如果没有足够量的数据支撑误差会很大,此时就结合生产经验,通过排土场排废超标统计(生产样从取样到化验成果出来平均所需时间在2h 左右,现将出现排废品位超标的出矿点认为这2h 均发生矿石流失,比实际值大)进行计算,得出损失率。
5 计算可采系数
通过测算,4—9 月采矿贫化损失率已经有测定的参考数据,因此便可按照可采资源量的计算公式,反算出4—9 月的月计划范围内可采资源量,计算结果如表3 所示。
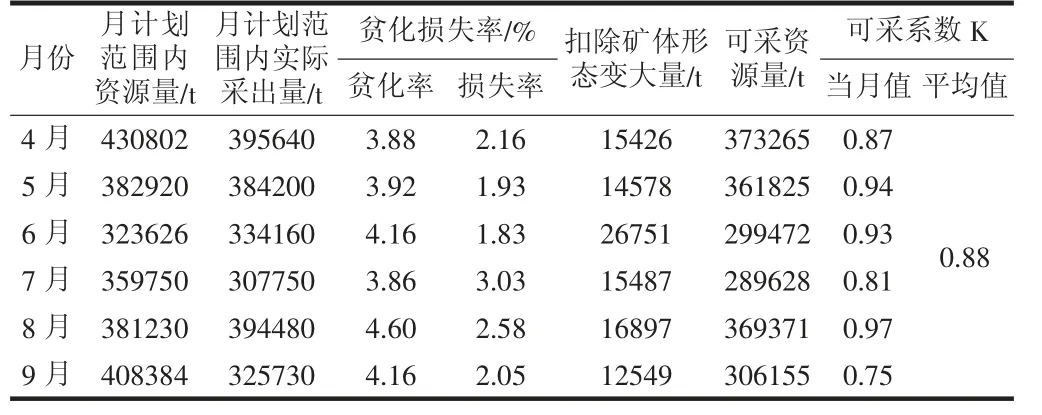
表3 2021 年4—9 月可采系数计算结果
利用间接法及反推法,对4—9 月生产数据进行分析处理,最终得出研究区的整体可采系数为0.88,但该项目需要研究不同规模矿体的可采系数,故还需要将研究区的整体可采系数进行按矿体规模分算。实际生产中,计划范围内的实际采矿量与采矿方法、矿体形态规模息息相关,故矿体规模划分的依据则选取文山都龙矿区精细化采矿方案中的划分标准作为参考,即矿体厚度小于3m 的矿体视为薄小矿体,矿体厚度3~5m 的矿体为中厚矿体,矿体厚度大于5m 的矿体为厚大矿体,计算结果如表4~表6所示。
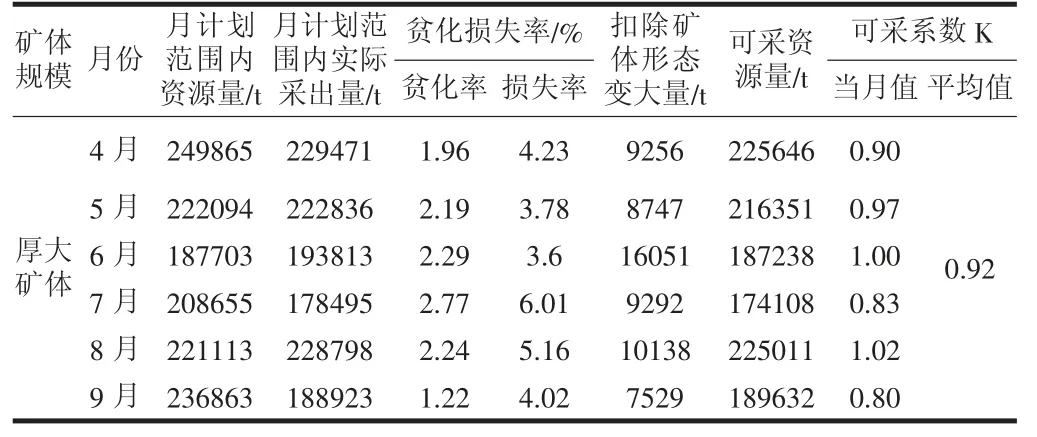
表4 2021 年4—9 月厚大矿体可采系数计算
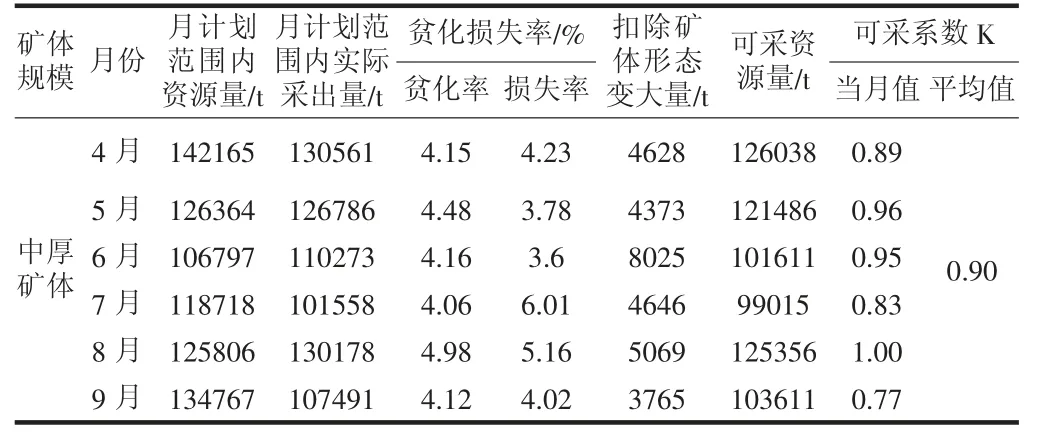
表5 2021 年4—9 月中厚矿体可采系数计算

表6 2021 年4—9 月薄小矿体可采系数计算
通过对研究区内的可采资源量、地质资源量、实际采出矿石量及贫化损失率的收集收集分析整理,最终计算得出薄小矿体的可采系数为0.88,中厚矿体的可采系数为0.90,厚大矿体的可采系数为0.92,如表7 所示。

表7 不同规模矿体可采系数归纳
6 结论
可采系数作为一个计算矿山可采资源量的计算参数,利用合理的可采系数计算出来的矿量能为矿山生产规划、矿山资源开采价值评估提供参考依据。但矿山可采系数受到矿区地质勘查程度、矿体的空间形态、采矿设计方法、采空区及坑道等多重因素影响,因此若通过直接法(正向计算法)计算其数值则需要收集大量的数据,结合国家及行业标准建立相关的数学评估模型去评估各个因素的影响数值、影响程度,这是一个过程复杂且容易产生较大评估误差计算方式。故本文结合实际情况,通过间接发(反向计算法)的方式,推算出矿山矿体的可采系数。
通过反推法计算可采系数,其实就是对矿山地质矿量与采出矿量关系的规律总结,该研究计算得出的可采系数,是通过对以往的数据处理而得出的,严格来说是一个经验系数。数据收集需要大量的工作量及时间,故本文在论证矿体可采系数时为节省工作量仅用了6 个月的生产数据作为基础数据,因此计算结果代表了这6 个月的实际生产可采系数。需要用这6 个月的生产数据计算出来的可采系数去代替整个矿山不同规模矿体的可采系数,其实还是有些数据不充分,所以还需要近几年的生产数据作为支撑。但本文主要是在论述一种计算可采系数的简易方法,重点是把该方法的计算过程及为什么要这么计算进行阐述,如需要计算更准确的可采系数,可加大基础数据的收集后整理计算。
该研究通过反推法计算可采系数其优点是:可不考虑影响可采系数的各类因素及其影响程度,可以把这些因素都归为一个整体因素,仅通过测算、计算统计出来的贫化损失率、地质矿量及实际采出矿量便可按照公式计算出矿体的可采系数,计算方法简单;缺点是:矿山贫化损失率的测定也是矿山数据测算的一份难点工作,贫化损失率数据的准确性、可靠性决定着可采系数的准确率。
