基于多项式拟合法的位场分离研究

李小娜

(成都理工大学 地球物理学院，成都 610059)

0 引言

重力异常是地下地质体不均匀的密度分布的综合反映。在需要解决所存在的地质问题时，人们总是希望能够得到目标地质体的重力异常，从而进行反演解释，计算出地质信息的目标密度，这种从已知的重力异常中获取目标地质体重力异常的过程通常称为重力异常分离(即位场分离)。在矿产资源勘查中，重力勘探是不可缺少的重要方法，人们在生产实践中已经证明，数据处理是重力勘探中重要的环节之一，重力异常位场分离技术是重力异常数据处理中的一项重要工作。地下不同深度、不同形态、不同规模以及不同物性大小的地质体引起的重力异常的“叠加”就是空间分布的重力异常，是一种体积效应，其中包含了很多很宝贵的信息，若能从观测数据中将目标地质体从重力异常中分离出来，就可以更进一步地研究其地质含义，较好地进行重力异常解释和反演。

目前重力异常的处理方法已由手动转变发展为自动，且方法众多。此处我们主要讨论不改变刚量的分离方法(波数域[1]和空间域)—空间域法。被广泛应用的空间域方法包括平均场值法[2]、圆周法[3]、趋势分析法[4]、插值法[5]等。平均场法是在一定剖面上或一定面积内的重力异常可看做是线性变化的，其平均重力异常值可以看做是这一剖面或者平面中心点的区域异常值，这时对于局部异常来说，它的范围应该小于或者等于所求的平均异常时所选用的范围[6]。需要指出的是平均场法在应用中会带来“虚假异常”的问题，人工用图解法勾绘区域异常时，就可以避免这一问题。最小二乘法是在一定长度内(剖面上)或一定面积内(平面上)的重力异常图中，一般将区域场看作是按照线性关系发生变化的，这时根据偏差平方和最小求出待定系数，就可得到区域场异常[7]。最小二乘法在运行中速度快、简单易实现，但是对于数据点多、复杂的多变量高次曲线，此方法使用的很少。插值法实质是用受局部场干扰很小或完全不受局部场干扰的测点(称为插值节点)上的场值来构造一个插值函数，然后用这个插值函数来计算受到干扰地段的区域场值[8]。最后实测值与所求得的区域场值的差，即为局部场值。目前插值函数种类繁多，近年来所提出的切割插值法具有划分精度高、畸变小和处理速度快的优点[9-10],但是在具体应用时需要对局部场进行定量，且具体深度会产生一定的误差[11]。多项式拟合法(趋势分析法)是目前重力资料数据处理中常用的方法，当参数选择恰当时可以获得比较理想的位场分离效果。多项式拟合是利用全区所有测点上的数据，趋势分析法的坐标原点是固定的而不是滑动的，所以需要将所有待定系数都求出来，才可以获得各测点上的趋势值[12]。Agocs[13]提出多项式拟合法，至今已被很多研究者证实。自21世纪开始，熊光楚[14]指出运用自调节趋势分析法实现位场的分离，该方法的优势在于能消除局部场对拟合区域场的多项式系数的影响；羊春华[11]用筛选-趋势分析法进行位场分离，认为该方法在分离效果上较常规方法更准确、更完全；周锡明等[15]提出变阶滑动迭代趋势分析法，在应用于某油田重力数据后表明其能有效地提取微重力异常，且反映出的地质效果良好。另外，李春芳[16]、杨培胜[17]、 英高海[18]等都对多项式拟合法进行了不同的研究。刘金钊，朱吕涛等[19]利用双线性鞍状函数进行多项式拟合位场分离处理，并将其应用在川滇地区的实测重力数据上，证明了该算法的实用性。

每种重力异常分离方法都有其相应的条件，因此，选择合适的位场分离方法，合理、正确地进行位场分离，获得与研究对象有关的异常，是解释和反演重力数据的关键步骤。近年来，我国进行了广泛地面重力测量，获得了大量的高精度重力数据，充分利用这些资料进行局部构造和区域构造的研究，对进行直接或间接勘探具有重要的意义。因此，笔者研究的多项式拟合位场分离方法具有重要的理论意义和现实意义。

1 算法原理

利用全区测点上的数据，根据测区内某一小范围内的已知重力异常值的变化趋势，建立一个拟合多项式，以一定阶次的数学曲面来代表测区内异常变化的趋势，并且用这个趋势作为区域异常来看待，然后从同一点的布格异常值中减掉这一区域异常即可获得测区内的局部异常，再用局部异常绘制局部异常平面图或剖面图。

在求区域异常时，必须求出拟合多项式的所有系数，以便利用它以及测点的坐标求出各测点的趋势值，亦即区域异常值(当拟合多项式的阶次不同时，多项式系数的数目也不同)。

按偏差平方和最小的原则选取拟合曲线，并采取二阶多项式方程为拟合曲线的方法，称为最小二乘法。以二次曲面拟合说明方法的基本原理[20]。设趋势面为：

(1)

其中:aj(j=0,1,2，…，5)为待定系数。如果在测区中按一定的网格选取了n个点，其坐标为(xi+yi)相应点上的布格异常值为gi(i=1,2,3，…，n)。则要是二次多项式所代表的曲面(趋势面)能与重力异常的变化在最小二乘方的意义下得到最佳拟合，系数ai应满足：

min

(2)

根据多元函数求极值得的法则, 式(1)成立的条件是:

(3)

于是，可以得到一个包含有多项式待定系数aj(j=0,1,2，…，5)的线性方程组(4)。它的矩阵形式为：

ATAX=ATg

(4)

其中:AT为A的转置矩阵。式(4)中的列矢量矩阵分别是：

(5)

利用相应的方法解出待定系数aj，然后利用式(1)，便可根据每个网格点的坐标(xi,yi)。最后绘出趋势异常(区域异常)图和剩余异常图。

2 模型搭建及分析

研究不同形状的地质体在地面产生的重力异常及其特征，是对实测异常进行解释的基础。一般通过建立正演模型，并对其进行处理和解释来验证数据分析、地质解释和重力反演的理论方法是否正确。因此，研究正演是反演的基础，位场正演计算，长期以来一直都为地球物理工作者们所关注。根据正演理论，我们可以搭建不同的合成模型。趋势分析法在建立正演合成模型时需要对用到的盆地基底进行扩边处理，笔者对断点数据进行了外扩，外扩的范围相对局部场很大，因此可以忽略边界效应。

根据最小二乘法，可用每个坐标点的坐标x计算出该点的重力异常值g。然后求出局部异常，绘出趋势异常(区域异常)和局部异常图。

(6)

2.1 模型搭建

笔者建立了两个不同的地质模型来客观评价多项式拟合位场分离方法的效果，如图1所示。图1(a)为模型一，其参数为：直立板状体密度为0.3 g/cm3，直立板状体在Z方向的顶底深度分别为1 km和4 km;水平方向视厚度为10 km;顶界面中心横坐标为95 km;板状体向下延伸的方向与X轴正方向所成角度为45°。盆地基地在X坐标范围为(0 km～200 km)上，每间隔5 km取一个点，共取41个点。

图1(b)为模型二，其参数为：直立板状体从1-3的密度依次为0.3 g/cm3、0.5 g/cm3、0.3 g/cm3，在Z方向的顶底深度依次分别为1 km和3.1 km、1.5 km和4.7 km、2 km和4.1 km，水平方向视厚度依次为12 km、9 km、12 km,顶界面中心横坐标依次为160 km、30 km、100 km，板状体向下延伸的方向与X轴正方向所成角度依次为90°、45°、90°。

图1 模型Fig.1 Model(a)模型一;(b)模型二

2.2 模型分析

图2(a)、图3(a)分别为模型一与模型二的叠加异常，理论区域异常和理论局部异常，依次作为对照来分析经过多项式拟合之后所得到的区域异常和局部异常的可靠性和有效性。由图2(b)，图3(b)可看出，当测区范围较小，基底起伏相对简单时，经多项式拟合法得到的区域异常与理论异常相同，得到的图1(c)局部异常与理论局部异常形态几乎相同。

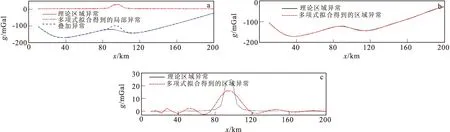
图2 模型一重力异常Fig.2 Gravity anomaly in model 1(a)重力异常理论值;(b)理论区域异常与多项式拟合法得到的区域异常;(c)理论局部异常与多项式拟合法得到的局部异常

图3 模型二重力异常Fig.3 Gravity anomaly in model 2(a)重力异常理论值;(b)理论区域异常与多项式拟合法得到的区域异常;(c) 理论局部异常与多项式拟合法得到的局部异常

图4 模型一选择低阶多项式(2次)得到的重力异常Fig.4 Gravity anomalies obtained by selecting lower order polynomials of the model 1(a)理论区域异常与经多项式拟合得到的区域异常;(b)理论局部异常与多项式拟合得到的局部异常;(c)理论叠加异常与多项式拟合得到的叠加异常

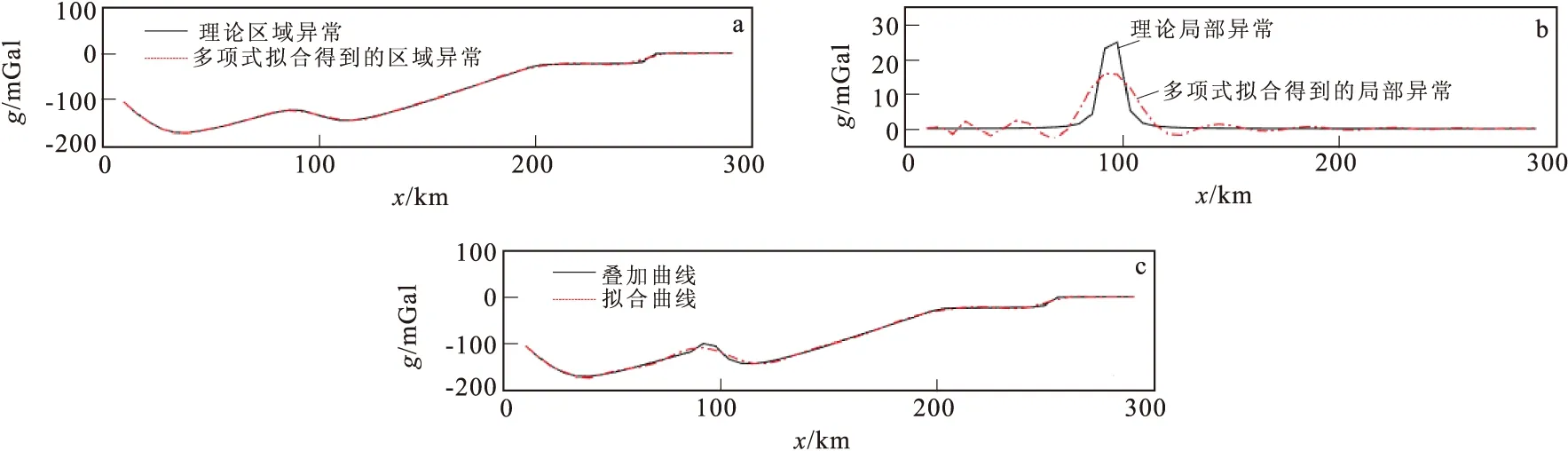
图5 模型一选择高阶多项式(9次)得到的重力异常Fig.5 Gravity anomalies obtained by selecting higher order polynomials of the model 1(a)理论区域异常与经多项式拟合得到的区域异常;(b)理论局部异常与多项式拟合得到的局部异常;(c)理论叠加异常与多项式拟合得到的叠加异常

图6 模型二选择低阶多项式(5次)得到的重力异常Fig.6 Gravity anomalies obtained by selecting lower order polynomials of the model 2(a)理论区域异常与经多项式拟合得到的区域异常;(b)理论局部异常与多项式拟合得到的局部异常;(c)理论叠加异常与多项式拟合得到的叠加异常

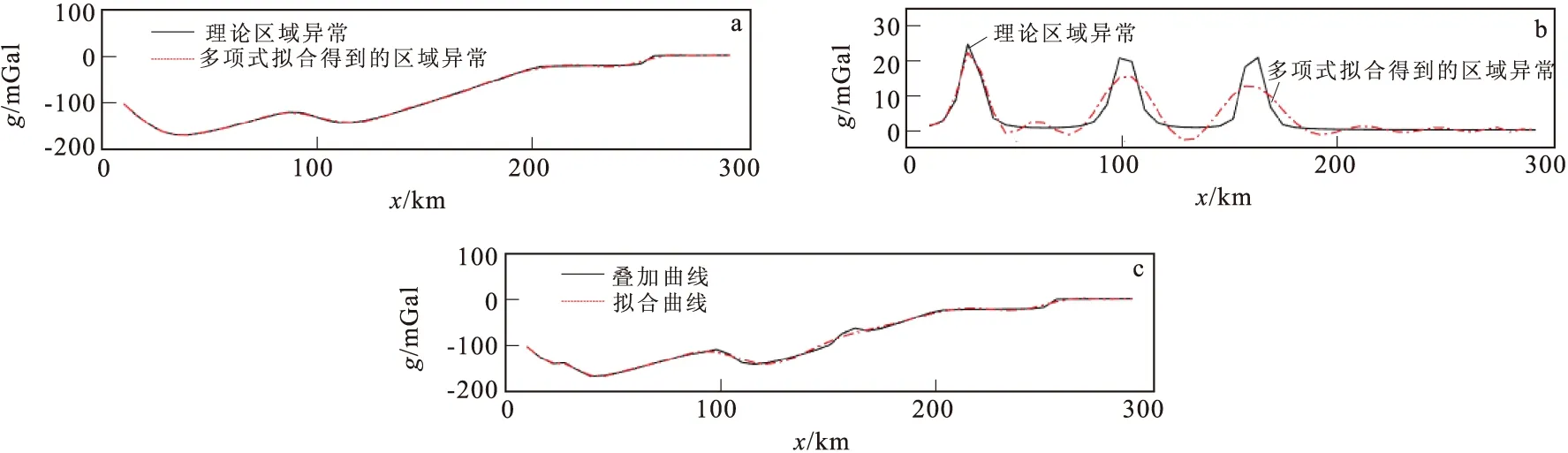
图7 模型二选择高阶多项式(12次)得到后的重力异常Fig.7 Gravity anomalies obtained by selecting higher order polynomials of the model 2(a)理论区域异常与经多项式拟合得到的区域异常;(b)理论局部异常与多项式拟合得到的局部异常;(c)理论叠加异常与多项式拟合得到的叠加异常

图8 模型一选择不同阶次多项式得到的重力异常Fig.8 Gravity anomalies obtained by selecting polynomials of different order in Model 1(a)区域异常;(b)局部异常

当测区范围较大，基底起伏又复杂时需要的多项式阶次就越高，其得到的局部场异常并不是越好，经多项式拟合法得到的区域异常与理论异常在小波长附近的吻合度较小，得到的图3(a)局部异常与理论局部异常在长波段形态相似。

图4～图7可看出，将相同直立板状体(局部场)放在相同盆地基底(区域场)的不同位置，盆地基底(区域场)本身的多项式拟合阶次没有变化，但是直立板状体(局部场)和叠加异常多项式阶次发生很放大变化。不同直立板状体(局部场)放在相同、不同的盆地的相同位置其盆地基底(区域场)本身的多项式阶次没有很大变化，但是直立板状体(局部场)和叠加异常度多项式阶次仍然会发生很放大变化。当盆地基底本身的起伏很大很复杂时，其自身的多项式阶次就会很大。当拟合的多项式的阶次特别高时，拟合曲线会产生震荡，扭曲区域场的形状，获得的局部异常分布会不精准。

由8图可以看出，模型1的盆地基地拟合曲线经过7次后几乎与原盆地基地曲线重合，直立板状体拟合曲线经过8次后与原直立板状体曲线很相近,在第9次拟合时出现了反向虚假异常。

由图9可以看出，模型2的盆地基地拟合曲线经过10次后几乎与原盆地基地曲线重合，直立板状体拟合曲线经过12次后才与原直立板状体曲线很相近。

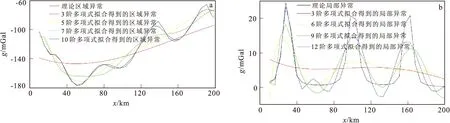
图9 模型二选择不同阶次多项式得到的重力异常Fig.9 Gravity anomalies obtained by selecting polynomials of different order in Model 2(a)区域异常;(b)局部异常

由图1～图9可看出，相同直立板状体(局部场)放在相同、不相同的盆地基地(区域场)的不同位置，盆地基地(区域场)本身的曲线拟合次数几乎没有的变化，但是直立板状体(局部场)曲线拟合次数发生很放大变化。不同直立板状体(局部场)放在相同、不同的盆地的相同位置其盆地基地(区域场)本身的曲线拟合次数没有很大变化，但是直立板状体(局部场)曲线拟合次数仍然会发生很放大变化。当盆地基地本身的起伏很大很复杂时，自身的拟合次数就会很大。

3 实测数据应用

这里实测重力剖面数据来自于辽宁省葫芦岛市杨家杖子镇经济技术开发区黑鱼沟某矿洞。该区域上构造活动强烈,主要为断裂构造,燕山期的岩浆活动也很强烈,区域矿产资源丰富.由于构造及虹螺山岩体岩浆热液作用,区内蚀变,矿化程度较强,具有较好的成矿条件.矿体主要赋存于岩浆岩及地层的接触带(矽卡岩带)内,区内矿床类型主要为矽卡岩型.蚀变破碎带,矽卡岩化等是主要的找矿标志。矿洞位于黑鱼沟西山寒武系下方，是铅锌矿开采矿洞。矿洞断面为马蹄形，水平延伸近50 m，可近似为一个无限长的水平圆柱体。矿洞中心埋深为5 m，高和宽均约2 m(图10)。在地面采集重力数据，重力观测剖面垂直于矿洞走向。

图10 矿洞位置及剖面形态Fig.10 Location and section shape of ore hole

观测布格重力异常如图11(a)中的实线。用多项式拟合法对该数据进行拟合得到区域(背景场)场(图11(a)中虚线)；去掉区域场(背景场)后得到的局部重力异常如图11(b)所示。对比图12[21]应用非线性滤波分离法得到的局部重力异常，本文方法得到的位场分离效果与实际情况基本一致，可以应用本文得到的位场分离效果确定场源、断裂位置及密度界面。

图11 实测重力数据异常分离Fig.11 Anomaly separation of measured gravity data(a)实测重力布格异常和经多项式拟合得到的区域重力异常;(b)分离后得到的局部异常

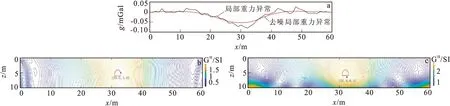
图12 石甲强Fig.12 Shi Jiaqiang(a)实测布格重力异常和分离的区域(背景)场;(b) 局部重力异常(实线)及去噪后的局部重力异常(虚线)；(c)基于向下延拓Milne法的重力归一化总梯度剖面

4 结论及建议

场分离结果的好坏直接影响着最终解释结果。笔者依据正演模型，对多项式拟合法在位场分离中的应用进行分析，得出以下几点认识：

1)在利用趋势分析法划分区域异常和局部异常的效果，主要取决于所建立的数学模型与实际区域重力异常分布的近似程度，但测区的范围比较大，地质条件又比较复杂时，它的区域异常就不一定能用某个固定的多项式来表示，所以应用本方法时必须结合区域地质条件，对测区的区域异常进行分析。

2)多项式拟合法在建立正演模型时要进行扩边处理，并要将边界效应降低到可忽略不计。

3)在对同一组模型采用多项式拟合算法，并不是拟合次数越多，相对误差越小，效果越好。相反，当拟合次数很大时，拟合得到的曲线会产生震荡。多项式阶次的选择，原则上应视区域场的复杂程度来定。阶次太高，会出现趋势值受局部场的影响较大的现象，因而会削弱局部异常的划分，同时也使趋势面畸变。因为阶次增加时，方程组解的误差会急剧增加。

4)虽然在这里的模型试验中利用多项式拟合法进行位场分离的效果较好，但是由于位场分离涉及到的实际地质情况较为复杂，多项式拟合法对于短波长的异常刻画仍存在问题，下一步将融合其他方法进行进一步研究。

致谢

感谢吉林大学地球探测科学与技术学院肖锋副教授和石甲强同学向本文作者提供实测重力数据！感谢成都理工大学图书馆为我们提供讨论场所和文献资源！