基于主成分分析的融合方法在断裂识别的应用研究

2022-01-06孙华军何建军

物探化探计算技术 2021年6期

王睿, 李琼,b, 孙华军, 何建军

(成都理工大学 a.地球物理学院，b.地球勘探与信息技术教育部重点实验室,c.信息科学与技术学院(网络安全学院、牛津布鲁克斯学院)，成都 610059)

0 引言

近年来，随着储层勘探技术的日趋成熟，地震属性能够广泛地应用于地质构造解释、储层预测、地质异常体的分析等各个方面，不同的地震属性反映地震数据体中的不同信息，可应用于不同的研究对象，如相、曲率等几何属性常应用于裂隙、河流道等地层不连续性现象的检测研究。

然而，地震属性属于一个很大的范畴，种类繁多，并且各个属性与所研究的地质对象之间存在着十分复杂的关系。这导致单个地震属性对于地震解释分析必然存在着多解性与局限性，需要多个地震属性进行综合分析[1]。

地震属性融合技术是建立在地震属性联合分析的基础上，不断发展的储层预测分析技术。丁峰[2]在RGB融合的基础上，以主成分分析(Principal Component Analysis)方法得到第四个属性分量，建立起RGBA(Red-Green-Blue-Alpha)颜色融合模型，用于属性融合的综合分析；姚威等[3]利用地震多属性融合技术研究目的层的沉积及地震反射特征，从而准确描述目的层位的沉积相展布特征；周游等[4]利用核主成分分析法，建立多个主成分变量代替原始多维测井信息，进行复杂岩性油气藏的浊积岩岩性识别，该方法实现了更高的岩性识别准确率，具有较高的应用潜力；潘拓等[5]利用主成分分析法优化BP神经网络的输入参数，以主成分特征值代替传统测井曲线油气参数，在优化网络模型结构、减少计算量的基础上，实现对有效储层岩性的准确识别。此外，主成分分析(Principal Component Analysis)在风险评估[6]、特征提取[7]、模式识别[8]、故障检测[9]等领域均得到了广泛应用。

1 主要采用的技术方法

1.1 主成分分析法

1.1.1 基本原理

主成分分析法(PCA)通过线性空间变换，以矩阵的降维思想把大量的地震属性转化为几个综合属性(即主成分)，在反映各个原始属性大部分信息的前提下，尽量减少信息之间的重复比例[10]，以综合属性代替原始属性进行解释与分析工作。

主成分分析法(PCA)的特点为：①得到的主成分个数远小于原有变量的个数，经过降维后的主成分能够代替原有的众多变量参与数据建模，较大幅度减少分析解释过程中的计算工作量；②得到的主成分是对原有变量集合进行数据重组的结果，因此其能够反映原有变量集合的绝大部分信息与特征；③通过主成分分析得到的新的综合指标(主成分)之间互不相关，所包含的信息互不重复，因此能够有效减少数据冗杂，避免信息重叠带来的诸多问题。

1.1.2 计算步骤

1)对原始数据矩阵X={x1,x2,…,xn}，进行标准化处理，以消除不同类型数据的量纲影响：

(1)

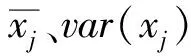
2)对经过标准化处理后的数据矩阵X，求其协方差；得到的协方差矩阵为矩阵X的相关矩阵，该相关矩阵R可表示为式(2)。

(2)

为了使数据处理过程得到简化，假定X仍表示标准化后的P维随机向量的原始数据矩阵X，则经过标准化处理之后的原始数据，其相关系数可表示为式(3)。

(3)

3)求原始数据矩阵X的一个正交矩阵a，使得a′a=1，并使方差Var(a′X)=a′Aa为最大值。根据矩阵的施密特正交化，求出相关系数矩阵的特征值(λ1,λ2,…,λp)和特征值所对应的特征向量分别为αi1、αi2、…、αip(i=1,2,…,p)。

4)将相关系数矩阵的特征值(λ1,λ2,…,λp)从大到小进行排序，其表示所包含的主成分信息由多到少。在实际应用中，一般选取各个主成分的累计贡献率超过85%的前n个主成分。

(4)

式中：λi表示第i个特征值；di表示第i个主成分的贡献率。

5)计算样品在n个主成分上的得分：

Fi=α1iX1+α2iX2+…+αpiXP

(i=1,2,…,n)

(5)

式中：α1i、α2i、…、αpi分别表示特征值λ1、λ1、…、λp对应的特征向量；Fi表示i个主成分的得分。

优选出的前n个主成分，包含地下构造和储层预测方面的绝大部分信息，在进行解释工作时，关键在于如何对提取的主成分做出合理解释；这一般需要结合主成分分析方法中表达式的系数进行定性分析。在分析解释主成分分量所表示的地质意义时，应与实际的地质构造与储层信息、测井数据相结合，才能做出合理的解释。

1.2 属性计算与提取

1.2.1 倾角和方位角属性

基于梯度结构张量(Gradient Structure Tensor，GST)改进的GST算法可以从地震数据体中提取倾角和方位角属性。GST算法计算得到的特征值可以对研究对象的张量、边角和连贯性进行定量和定性描述，通过计算局部方向梯度，可以进一步得到局部梯度结构张量GST，用于反映地震图像的纹理结构。

对于三维数据体，通过计算每个点的方向导数并建立梯度结构张量，可以得到梯度结构张量矩阵TG，可表示为：

(6)

对式(6)进行特征值分解为式(7)。

TGv=λv

(7)

式中：λ是矩阵TG的特征值；v是矩阵TG属于特征值的特征向量。其中，特征值λ1、λ2、λ3分别对应于特征向量v1、v2、v3。

因此，得到的三维地震数据的梯度结构张量矩阵TG包含三个梯度、六个张量及九个卷积，通过特征值分解得到的特征值λ1、λ2、λ3和特征向量v1、v2、v3包含了丰富的地质构造信息。可以构建倾角和方位角属性如下：

倾角属性：

(8)

方位角属性：

(9)

1.2.2 构形张量属性

构型张量属性的计算一般基于GST算法，通过特征值分解得到的特征值λ1、λ2、λ3和特征向量v1、v2、v3包含丰富的地质构造信息。根据特征值λ1、λ2、λ3可以得到其与三维图像结构的对应关系如表1所示，能够对不同纹理特征的沉积地貌单元进行刻画，如河道、沉积扇等。其中主要描述断层的构型张量表达式[11]，可由如下特征值计算得到混沌属性和Lamda横向梯度属性。

表1 梯度结构张量特征值与三维图像结构的对应关系

混沌属性：

(10)

混沌属性不仅能在切片上识别裂缝，而且在地震剖面上的裂缝识别也取得了较好效果[12]，并对河道边缘及弱能量杂乱反射有较为明显的刻画作用。

Lamda横向梯度属性：

Clamda=λ2+λ3

(11)

Lamda横向梯度属性具有较好的抗噪性，对河道边缘有着较好的刻画作用。

1.2.3 相干属性

Gersztenkorn A and Marfurt K J[12]提出了基于特征构造的第三代相干算法，自提出以来，便展示出了对细小裂缝和断层的良好检测能力，是目前应用最多、最主流的相干体算法。其直接利用倾角属性进行插值运算，对生成的协方差矩阵进行相干体计算，得到的相干属性体，主要用于裂缝、断层的相似性分析。

C3算法的相干值计算使用了C2算法中的协方差矩阵C，C表示为式(12)。

(12)

式中：T为矩阵的转置。

对协方差矩阵C进行特征值分解，可以得到特征矢量及各个特征矢量对应的特征值。其最大特征值赋存协方差矩阵C的信息量，可以作为特征构造相干性的估算，即可得到第三代相干算法的表达式为：

(13)

式中：(q,p)表示为视倾角；λmax为协方差矩阵C的最大特征值；λm为协方差矩阵C的第m个特征值。

相比第一、二代相干算法，第三代相干算法的抗干扰能力强，得到的相干属性体信噪比高，更适应于信噪比较低的地震数据体的断层、裂缝识别。

1.2.4 曲率属性

曲率表征的是二维曲线的形态结构特征，反映曲线上任意一点的弯曲程度。在地层的外侧受到构造应力作用，发生拉伸时，产生裂缝的概率较大，即曲率表示为正值；在地层的内侧受到构造应力作用，发生挤压时，产生裂缝的概率较小，即曲率表示为负值。当曲率值突然出现大的变化时，可以判断该处很有可能出现断层。

对于地震勘探而言，地震层位可视为三维空间中的一个构造曲面，使用最小二乘法或其他曲面构造方法拟合一个二次面z(x,y)：

Z(x,y)=Ax2+By2+Cxy+Dx+E

(14)

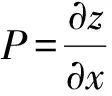
(15)

通过系数组合，可以得出各种曲率属性：

1)平均曲率：

(16)

2)高斯曲率：

(17)

3)极大、极小曲率：

(18)

4)最正、最负曲率：

Kpos=(A+B)+[(A-B)2+C2]1/2

Kneg=(A+B)-[(A-B)2+C2]1/2

(19)

5)倾向曲率与走向曲率：

(20)

2 工区概况

2.1 地质概况

本次研究工区为东营凹陷南斜坡东部的陈官庄地区，其东部接王家岗断裂构造带，西部被纯化—草桥断裂鼻状构造带阻隔，南临广饶北坡，北达牛庄生油洼陷区，总体上呈现北倾斜，并受断层切割的构造格局(图1)。

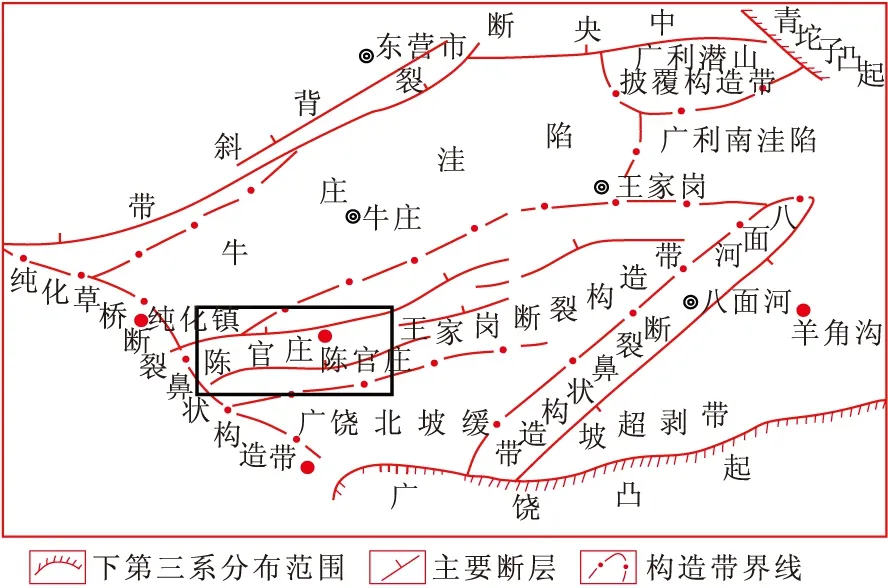
图1 陈官庄地质构造图Fig.1 Geological structure map in Chenguanzhuang

主要研究陈官庄地区的古近系沙河街组地层，该地层的埋藏深度较大，分布范围广，厚度较大。与下伏孔店组为连续沉积，是在盆地强烈裂陷期气候潮湿、汇水量充足的条件下形成的河流三角洲、深湖—半深湖沉积。该地区内部地层砂体的物性分布不均匀，砂体的空间展布在纵向与横向上的变化都很大，很难准确获取其空间展布情况。整个地区发育纯化-草桥鼻状构造带和王家岗断裂构造带，两个正向二级构造带内断层比较发育，主要断层方向为东南向西北延伸，并能够对局部构造进行改造，形成丰富的油气圈闭，为油气运移、聚集提供较多的通道。

2.2 地层概况

古近系沙河街组地层的层位可划分为Es1、Es2、Es3和Es4四个层位，其中Es3层为三角洲、水下扇等多种沉积发育的主要层位。整个沙河街组主要为砂泥岩互层，其中砂岩厚度较薄，砂岩类型包括灰色泥质粉砂岩、灰白色细砂岩以及含砾砂岩等。

研究区域内采样间隔为2 ms的三维地震数据，图2为第5 880号主测线地震剖面图，目的层位为T6强反射层上1 250 ms处。在整个剖面上，发育有一条断层，然而其内部的微小断裂在剖面上难以观察，需要研究目的层位的断裂结构特征，并检测裂缝的发育情况。

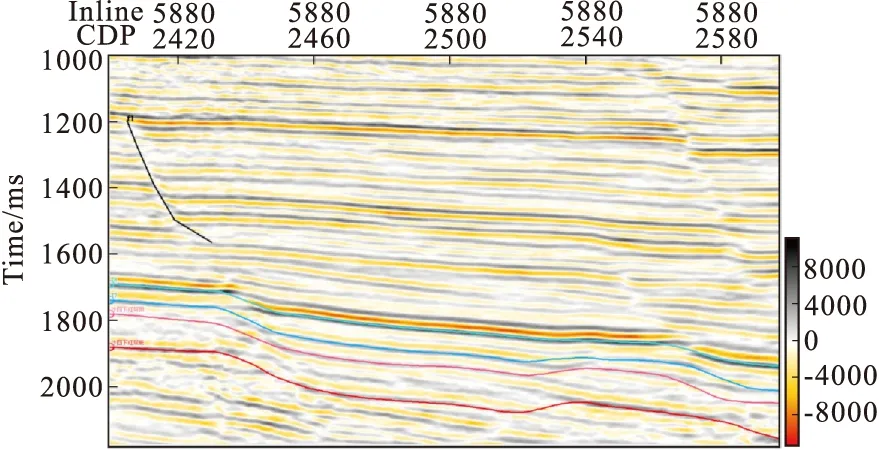
图2 第5880号主测线地震剖面图Fig.2 Seismic section of main survey line No. 5880

3 单属性分析

3.1 方位角倾角属性

方位角属性一般可以从大尺度上刻画研究区域的断裂发育系统，描述地层的走向和倾向特征。图3(a)为目标层位方位角属性平面图，在红色曲线标识的区域，方位角数值变化剧烈、差异明显。从大尺度上看，红色曲线标识区域是地层断裂和裂缝发育的集中区域。

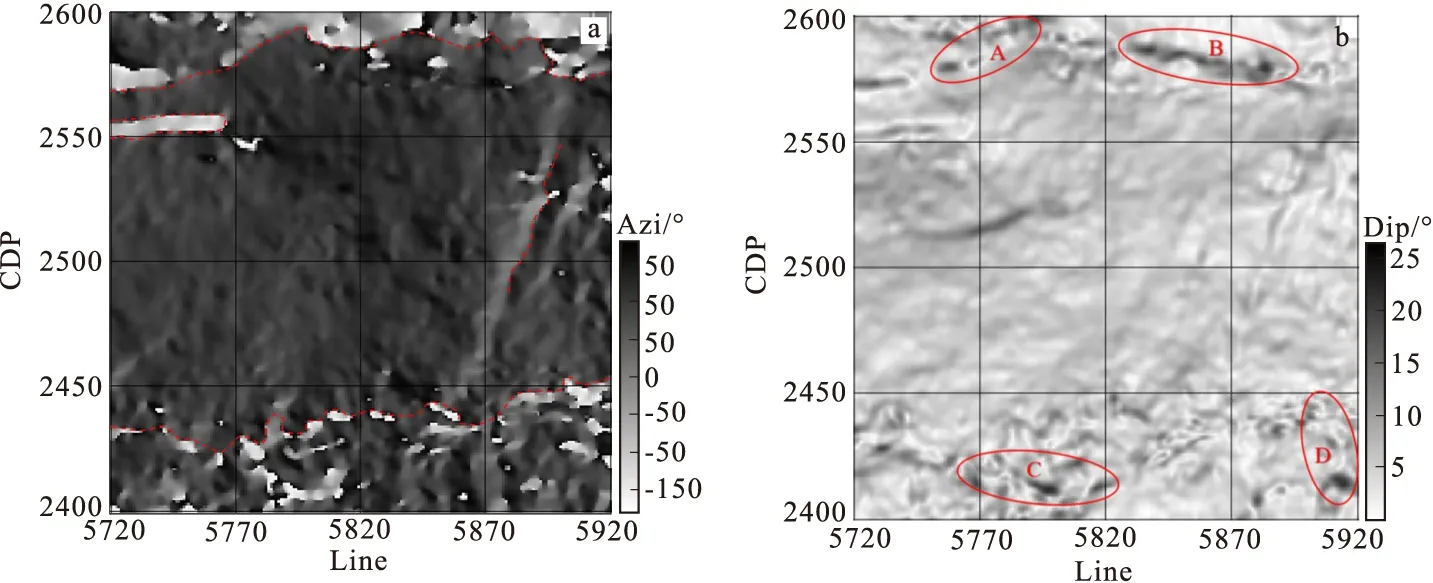
图3 目标层位方位角倾角属性平面图Fig.3 Plane view of target horizon azimuth and dip attributes(a)方位角属性;(b)倾角属性

倾角属性反映了裂缝发育带的平面展布情况，如图3(b)所示为目标层位倾角属性平面图，在红色椭圆标识的区域，倾角变化剧烈，并分布有细密的黑色条带，表明该处为主要的断裂发育区，其周围发育着一些小裂缝。

3.2 构形张量属性

构形张量属性中的混沌属性对河道边缘及弱能量杂乱反射有显著的刻画作用。因此提取混沌属性用来反映目标层位的裂缝发育情况(图4)。

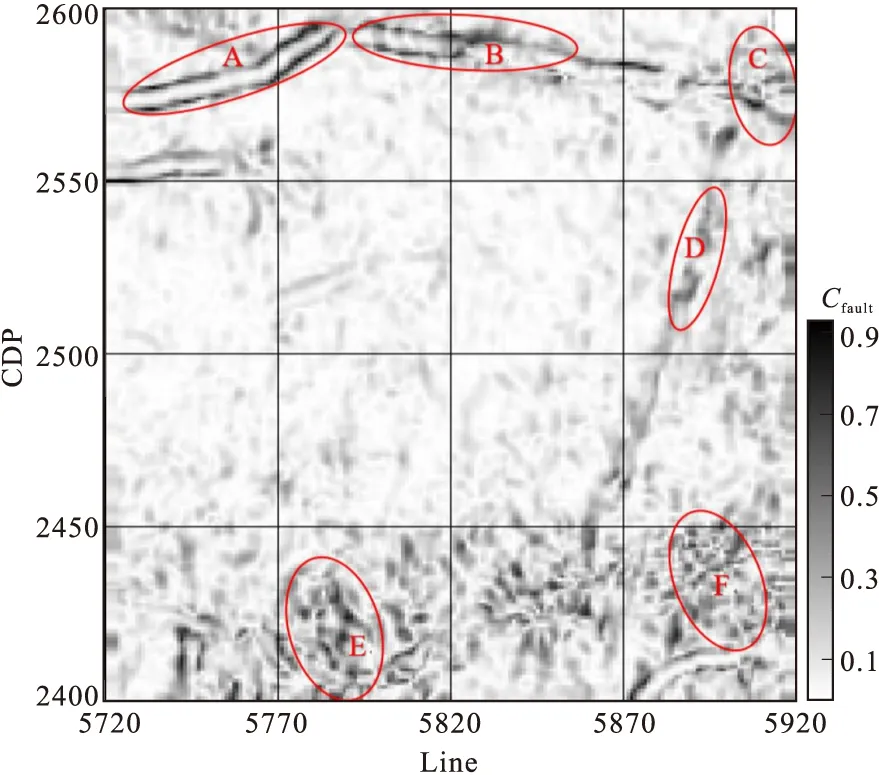
图4 目标层位构形张量属性平面图Fig.4 Attribute plan of target horizon configuration tensor

在红色椭圆标识的区域，断层因子分布呈现出团块状、短而弯曲的线状特征，对这些断层因子的特征进行连接，能够比较清晰地识别出主要裂缝发育区的边界范围，刻画出裂缝发育的边缘结构。较为集中的黑色区域表示裂缝发育程度较高；而大范围分布的白色区域表示该处裂缝发育程度差，地层的连续性较好。

3.3 相干属性

地震相干属性表征了地震波形同相轴的连续性，在地层岩性变化大、裂缝发育的地质区域，地震波形同相轴不连续，相干值较小；而在地层岩性变化小、无裂缝发育的地质区域，地震波形同相轴连续，相干值较高。因此，提取目标层位的相干属性对断层、裂缝进行识别，是非常有效的属性分析方法。

采用基于特征结构分解的第三代相干算法提取目标层位的地震相干属性(图5)。在红色椭圆标识的区域内，相干值较小，并呈条带状分布，表明地层的连续性较差，可以推断为裂缝的集中分布区域。

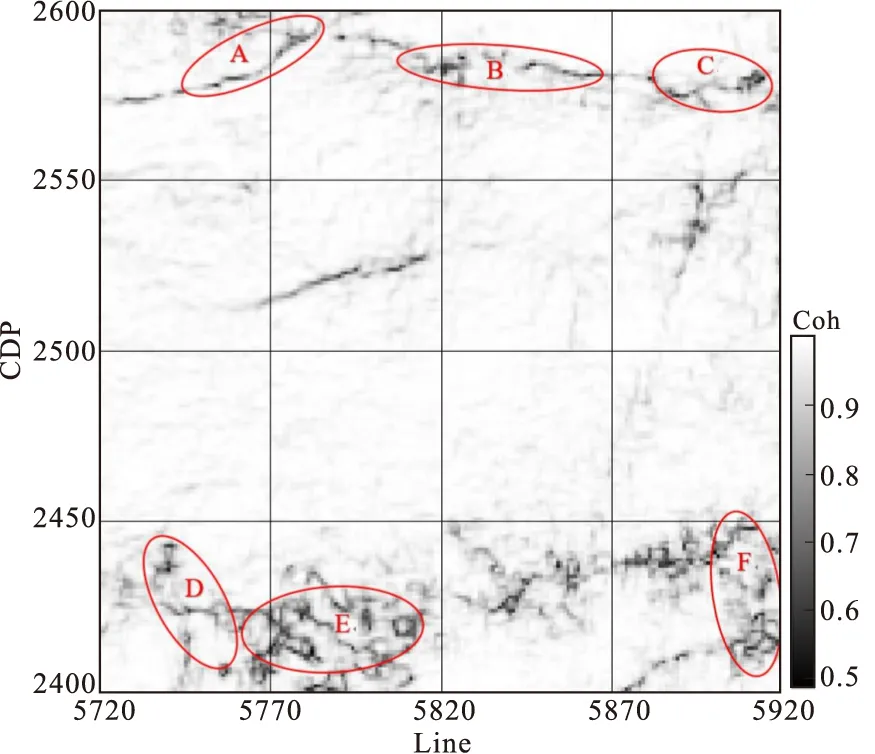
图5 目标层位相干属性平面图Fig.5 Coherent attribute plan of target layer

3.4 曲率属性

地震曲率属性能够反映目标层位的弯曲程度，对折曲、裂缝的反应十分敏感。图6为目标层位的曲率属性平面图，包括极大曲率属性、极小曲率属性、最正曲率属性、最负曲率属性。在红色椭圆标识的区域内，各个曲率值变化较大，能够非常模糊地识别到较大的断层发育情况，其原因可能是目标层位的地层较为平缓，且无较大的岩性变化。

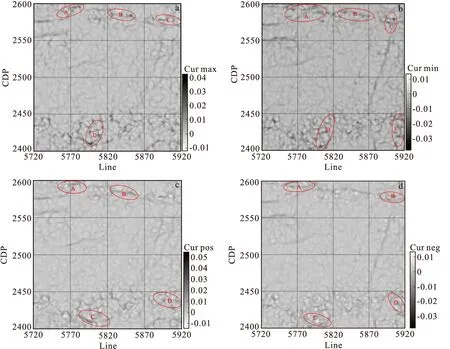
图6 目标层位曲率属性平面图Fig.6 Plan view of curvature attribute of target horizon(a)极大曲率属性;(b)极小曲率属性;(c)最正曲率属性;(d)最负曲率属性

4 融合属性分析

运用主成分分析法(Principal component analysis，PCA)，对用于单属性分析的方位角、倾角属性、混沌属性、相干属性和极大曲率、极小曲率、最正曲率、最负曲率属性进行融合处理，得到包含各个单属性特征的综合属性——第一主成分、第二主成分、第三主成分(图7)。

第一主成分(图7(a))包含了融合的各个地震属性的绝大部分信息，在整个沿层切片上，对存在的主要6个断层的发育方向和边界范围(图7黄色椭圆标识区域)都达到了非常清晰地刻画，其边缘存在的一些小裂缝也得到了较为清晰地刻画，同时，对于M处层位缺失也得到了有效反映，整体效果相比于各个单属性所反映的断层特征刻画更加突出，达到了融合属性进行综合分析的目的。第二主成分(图7(b))包含了部分地震属性信息，对存在的主要6个断层的发育方向和边界范围的刻画较为清晰，但其包含的地震属性信息较少，对于一些小裂缝的刻画不够清晰，与一些连续性较好的地层区分不明显。由于主成分分析法(PCA)得到的新综合属性(主成分)之间信息互不相关，第三主成分(图7(c))仅仅包含极少的地震属性信息，对主要的6个断层的刻画不清晰，只能对C、F断层的局部发育和边界范围有较清晰刻画。

图7 目标层位各主成分属性图和任意测线地震剖面图Fig.7 Attribute map of each principal component of the target horizon and seismic profile of segmented survey lines(a)第一主成分图;(b)第二主成分图;(c)第三主成分图;(d)任意测线地震剖面图

通过建立如图7蓝线标识的任意测线，并与包含目标层位的任意测线地震剖面(图7(d))进行对比，可以发现：任意测线所经过的A、B、C、D、E、F为6个主要的断层，与地震剖面上的f1、f2、f3、f4、f5、f6断层结构都能进行一一对应，并且地震剖面上断层发育的走向、倾角以及周围的裂缝发育程度都与第一主成分(图7(a))和第二主成分(图7(b))形成良好的对应关系，这表明基于主成分分析法的融合方法在断裂识别上是可靠的，识别的精度可以达到2 ms左右(大约6 m～8 m)，而在第三主成分(图7(c))由于地震属性信息的缺乏，无法反应出f1、f2、f4、f5断层，仅能识别出f3、f6断层的部分边界范围特征。