基于MPC 方法的风电场一次频率协调控制策略
2022-01-06赵文钦肖辉樊国旗林亚楠文章
赵文钦,肖辉,樊国旗,林亚楠,文章
(1.长沙理工大学电气与信息工程学院,湖南 长沙 410103;2.国网浙江省电力公司金华供电公司,浙江 金华 321001;3.湖南大学电气与信息工程学院,湖南 长沙 410012;4.国网湖南省电力公司检修公司,湖南 长沙 410004)
0 引言
近年来,传统化石能源的大量消耗引起了全球对环境问题的广泛关注,风能得到了快速发展。截至2019 年底,欧洲风力发电容量已达205GW:陆地183GW,海上22GW,占欧洲电力市场需求量的15%[1]。变速风力发电机接入电网数量增加,接口电力电子变流器具有输出有功功率与系统频率解耦的特性,导致系统频率漂偏移增加。因此,世界各地的电网都对风电场在过频和欠频区域维持系统频率稳定的能力提出了具体要求[2]。
目前,在系统频率调节中引入风力发电的研究已经相当多。文献[3] 验证了通过短期从WTG中模拟传统发电机特性的旋转惯量或超级电容中释放能量来实现一种虚拟惯量控制的方法。文献[4] 通过在转子侧变换器的控制回路中添加一个频率偏差项,将速度-转子特性重新引入到变速风机中,仿真结果表明,这种控制策略下的低频响应会提高转子转速,从而导致频率突然下降。文献[5] 提出了一种改进的风力发电机转速下降控制策略,通过将脱线控制与临时过度生产技术相结合,消除了频率突然下降后的转子加速相位。通过对叶片的俯仰或对机组转子的过伸,可以实现脱油操作,该技术的具体实施方案在文献[6-7] 中有详细介绍。
除了基于局部控制器优化的控制策略外,还有一些基于优化策略的控制方法,可以实现每个风机之间的协作和交互。文献[8] 在考虑风电场尾流效应的协调控制策略的基础上,对每个机组的转子转速和桨距角的静态参考值进行优化,以实现不同的运行模式切换。在文献[9] 中设计了一种分布式牛顿方法,以实现稀疏通信网络上风力发电机之间的快速协调。文献[10] 提出了一种风电场参与一次频率控制的模型预测控制方法,其中采用WTG 非线性动态模型来优化自身的动态行为。
本文提出了一种基于MPC 结构的数据驱动协调一次频率控制新方法,该方法可以较好地解决实际中大型风电场中各WTG 参数难以测量和估值的问题。在该方法下,不需要周期性的模型参数维护,从而节省大量的时间和人力。仿真结果表明,该方法能使风电场在频响过程中具有灵活的速度下垂特性,同时最大限度地减小转子转速畸变。
1 风力发电机模型
本文主要研究市场占比率较高的双馈式发电机(Doubly Fed Induction Generator,DFIG) 型风力发电机(Wind Turbine Generator,WTG) 的建模与控制问题,其叶片捕获机械功率如下:

式中,ρ表示空气密度,R表示叶片半径,vω表示瞬时风速,cp表示风能转换系数。风能转换系数由叶片桨距角θ,叶尖速比λ决定,其中叶尖速比λ定义如下:

式中,ω为机械角速度。
将转子轴的动力学模型简化为一阶惯性模型:

式中,H表示等效模型的旋转惯量,tm和te分别表示机械转矩和电磁转矩。
为了保证转子的转速安全,在DFIG 的局部控制器中配置桨距控制器,可在高速风力条件下调节捕获的机械功率。因其机械过程的特性,桨距调节器的响应通常较慢。
由于电气控制和动态过程通常在瞬时完成,通常可被视作在一次频率响应时间尺度下的静态模型。

式中,Pe表示DFIG 的输出有功功率,Pref表示输入控制器的有功功率参考值。通过对转子侧变流器内电流控制回路的d-q轴分解,可实现DFIG 的有功和无功控制的解耦以及对局部下垂控制方法的适应。
DFIG 的实际动态行为应该包括整个控制过程中的通信延迟、计算精度和驱动动力学,这几乎不可能通过经验推导的方式准确建模。因此,在现有的数据测量、存储和处理能力下,通过数据驱动的方法来揭示潜在的主导动态是一种更实用的方法。本文研究的一次频率控制问题主要关注每台WTG在频率响应过程中的自身状态稳定性。而转子转速稳定性则是最值得关注的控制指标。假设可测得瞬时风速与有功功率参考值,那么可以得到一个控制转子转速的WTG 离散动态模型:

式中,f表示控制输入以及状态变量之间的耦合关系,uk为输入控制矢量,由有功功率参考值和转子转速组成。
2 风电场控制策略
2.1 WTG 动态建模
由于控制输入与状态变量之间的动态耦合关系通常是非线性的,难以清晰地表达。实际应用中的解决方法是基于大数据集的移动快照对强耦合非线性关系进行局部线性化。设该对表示时间点k的扩展状态,包括当前输入和状态变量,序列应该基于现有工作点获取WTG 动态模型所需的信息。假设移动快照的长度为N,通过公式(7) 与(8) 对采集的数据局部线性化:

WTG 的线性动态模型可以表示为:

式中,S表示控制线性动态行为的矩阵。
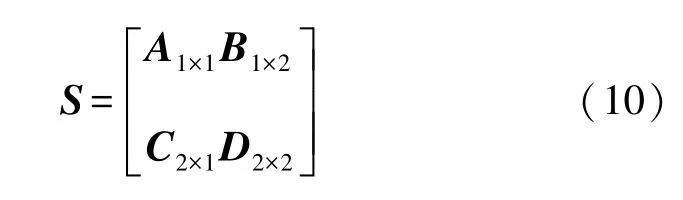
S可由最小二乘法[11]解出:

式中,†代表矩阵X的伪逆矩阵。
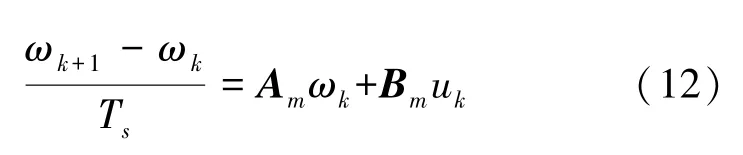
整理得到:

式中,Ai=AmTs+Ω,为离散系统矩阵;Bi=BmTs,为离散输入矩阵。
可以推出WTG 的控制模型:
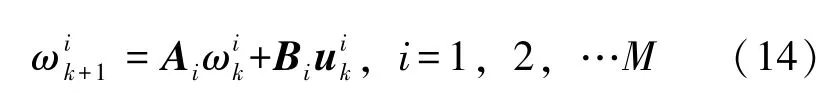
式中,M表示所控风电场中WTG 的台数。
2.2 控制模型结构
基于WTG 的控制模型,定义中心状态变量和输入向量:

由式(15),在单台风力发电机组模型的基础上,建立集中控制模型:

式中矩阵A和B由单台WTG 的状态转移矩阵建立:

式(16) 即为整个风电场动态模型,为了实现一次频率控制,稳定转子转速,提出MPC 控制方法:

式中,Kdf表示速度下降率,Qx表示两个控制目标之间的偏置系数,Δf为实际测得频率fmeas与参考频率fref的误差:


拟采用控制桨距角的方式调节有功,以实现频率调节的目的,故还需设置WTG 的初始状态:

风机通过桨距角θ的变化获得的有功功率P为:

式中,β0、ω0分别为初始桨距角和转子转速,而系统实际桨距角由风机实际转速与风机参考转速的误差值决定。
公式(18) — (24) 即为完整的风电场参与一次频率控制过程的MPC 过程。
MPC 方法具体执行步骤如图1 所示。

图1 MPC 流程
3 DFIG-WTG 系统仿真模型
3.1 仿真模型建立
为了验证所提方法的有效性,以IEEE9 总线系统为例,利用Matlab/Simulink 进行实例分析。图2 所示的系统由三个集成的DFIG-WTG 组和两个常规发电机组成。每组并联50 台容量为1.5 MW的WTG。两台同步机容量分别为250 MW 和200 MW。总能耗为315 MW,风电占比超过40%。考虑到一次频率响应时间,将仿真时间设置为10 s,图3 展示了此期间各机组风速变化情况。单台WTG 模型和风电场控制器的详细参数见表1。

图2 系统仿真模型

图3 各机组风速变化图

表1 风电场控制器与WTG 参数
3.2 低频仿真分析
在MPC 策略基础上,同时加入本地下垂控制(Local Droop Control,LDC) 策略。将负载波动设定为0.5 s,步长增加10%。在没有风电参与频率响应过程时,负荷波动会导致频率严重下降至48.8 Hz 附近。为验证所述控制策略,采取两种不同方案进行对比。在方案一中,使MPC 控制器的速度下降率与LDC 控制器保持一致,调频结果如图4 所示。
可以看出,当风电参与调频时,负荷波动引起的频率偏移被限制在0.5 Hz 以内,避免频率恢复过程中发生超调。MPC 策略下的频率变化与LDC策略几乎没有差别。图4 中整个风电场的输出有功功率变化曲线也表明MPC 控制器与LDC 控制器具有相似的控制效果。这是因为MPC 控制器主要关注并追踪系统操作者给出的速度下垂特性。

图4 系统频率变化图(方案一)

图5 风电场输出有功变化(方案一)
除频率调节外,转子转速平滑下降是频率控制过程中的另一个重点。在此,从整个风电场的角度定义转子转速畸变的平均水平:
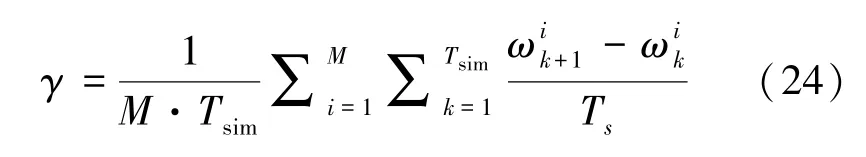
表2 中,风电场参与调频使得转子转速变化显著增加。但通过优化不同风速的WTG 机组的有功功率基准可以稳定WTG 转子转速,从而达到延长部件使用寿命的目的。MPC 控制器的平滑效果如图6—8 所示。

表2 转子转速畸变率变化对比(方案一)

图6 机组一转子转速变化图(方案一)

图7 机组二转子转速变化图(方案一)

图8 机组三转子转速变化图(方案一)
3.3 下垂变化特性
协调控制策略的一个突出优点是风电场的下垂特性变化灵活,可以在短时间内通过调整局部控制器参数来改变该特性。
在方案二中,将速度下降率提高至0.3 p.u./Hz,图9 表示相同负载条件下不同控制策略的结果。MPC 控制器使风电场参与调频更加灵敏。因此,设置一个较小的频率偏移值0.4 Hz,使其与电网要求的0.5 Hz 保持一定裕度。从图10 可以看出,在协调控制模式下,风电场的参与可以使系统频率更加稳定。上述结果表明,采用协调频率控制策略的风电场能更加灵活地接受上级调度指令,与电网进行交互,同时有效地调整速度下垂特性。
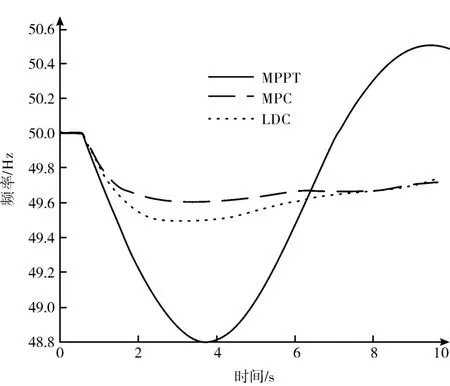
图9 系统频率变化(方案二)

图10 风电场有功输出变化(方案二)
三组风机的转子转速变化情况如图11—13 所示,转子转速变化情况见表3。可以看出,随着转速下降率增大,转子转速波动也随之增大。各机组的平均转速也因调频过程的功率汲取而降低。考虑到风电场提供频率调节服务的经济效益,可以通过设置相应控制器来平衡增加的机械负荷。

图11 机组一转子转速变化图(方案二)

图12 机组二转子转速变化图(方案二)

图13 机组三转子转速变化图(方案二)

表3 转子转速畸变率变化对比(方案二)
4 结论
提出一种基于MPC 方法的风电场频率协调控制策略,该策略优化频率响应过程中造成的转子转速畸变。该策略的优点主要有两方面:利用不同工况下WTG 之间的相互作用平滑转子转速波动;具有灵活的速度下垂特性,响应迅速,满足实际操作需求。仿真结果也验证了风电场外部频率响应与内部转子转速稳定性之间的平衡。
