基于18 相风力发电系统的最大功率跟踪控制策略研究

周诗嘉，杨光源，彭光强，武霁阳，辛清明

(1.湖南大学电气与信息工程学院，湖南 长沙 410082；2.中国南方电网超高压输电公司检修试验中心，广东 广州 510663；3.南方电网科学研究院有限责任公司，广东 广州 510080)

0 引言

随着新能源发电技术的广泛应用[1－2]，风能作为一种可再生能源，具有安全、清洁、储量丰富的特点[3－4]，因而风力发电越来越受关注[5]。

国内外关于多相电机的研究也相当成熟，文献[6] 将多相电机应用于舰船中压直流综合电力系统，实现了系统高精度实时仿真；文献[7] 将多相电机应用于电动汽车，达到了效率高、响应快以及可靠性高的要求；文献[8] 从磁密、转矩、转矩脉动以及容错性能等方面考虑，五相十槽十二极电机应用于高可靠的航天伺服系统；文献[9] 研究了双Y 移30°永磁同步发电机在航空高压直流电源供电系统中的容错控制，提升了系统抗扰能力。与传统电机相比，多相电机具有结构简单、可靠性高、转矩脉动低等优点，适用于低速、大功率的场合[10]，但将多相电机应用于风力发电中却鲜有研究。

在一定的风速下，对应着风机的一个最优转速，以实现风能的最大捕获。因此，为提高风电机组的发电效率，需要寻找实际风速波动时的最佳转速，即最大功率跟踪控制，这也是风力发电的关键问题之一[11]。目前，风力发电机组的最大功率跟踪控制方法主要分为叶尖速比法、功率信号反馈法和爬山搜索法。叶尖速比法控制比较简单，但需要对风速的测量十分精准，且最佳叶尖速比曲线对风机的结构依赖性太强，后期维护比较复杂[12]。功率信号反馈法需要大量的仿真计算，难度较大，且需要获得最佳功率曲线，对风机结构存在较强的依赖[13]。爬山搜索法不需要精确测量风速，摆脱了对风机模型参数的依赖，但风机的惯性和风速的波动，使得爬山法捕获最大功率点扰动时间长[14－15]。

基于以上研究，本文采用了18 相直驱永磁同步发电机经三相桥式不控整流后与隔离型DC/DC变流器相连接，DC/DC 变流器的输出端通过模块化多电平变流器并入高压直流电网的拓扑结构；此外，通过计算和推导得出最大功率点对应的三相桥式不控整流器的输出电流总是恒定的，即可以通过控制输出电流来调节隔离型DC/DC 变流器的占空比，从而调节风机转速，捕获最大风能；通过对隔离型DC/DC 变流器的输入电流进行反序法分配，实现模块化多电平变流器电容电压的平衡。该方法控制简单，且不受风速波动的影响，大幅降低了成本。

1 风力发电系统拓扑结构

基于18 相直驱永磁同步发电机的风电系统拓扑结构如图1 所示。18 相永直驱磁同步发电机含有6 套三相绕组，两套相邻的三相绕组之间互差10°电角度。各套三相绕组都与一个三相桥式不控整流器相连，三相桥式不控整流器输出端后接N个并联的隔离型H 桥DC/DC 变流器，每个DC/DC变流器与一个MMC 半桥子模块相连，所有的MMC半桥子模块相连并和一个电感L串联。该串联电路的输出端与高压直流电网相连，并联的DC/DC 变流器个数N由高压直流电网的电压Uhvdc和三相桥式不控整流器直流侧输出电压Uo决定，可以表示为:

图1 风力发电系统拓扑结构

式中，nphase为多相风机的相数，此方法仅适用于相数为3 的整数倍的情况。为提高系统的容错性能，高压直流电网侧电压可以设为所有MMC 半桥子模块电压之和的5/6 倍，在某一套三相绕组发生故障后仍能保证系统正常运行。

2 最大功率跟踪控制策略

传统的三相电机实现最大功率跟踪控制按照后接变流器的类型不同，可分为矢量控制和控制DC/DC 变流器占空比的方式。目前多相风机也大多采用矢量控制的方法，但随着多相风机相数的增多，矢量控制的方式也随着矢量元素指数形式的增长而更加复杂。因此，对于所采用的18 相直驱永磁同步发电机来说，矢量控制不再适用，采用三相电机后接三相桥式不控整流器和DC/DC 变流器的结构，通过控制三相桥式不控整流器的输出电流来改变DC/DC 变流器占空比，从而达到端电压控制及最大功率跟踪的目的。

2.1 三相桥式不控整流器机理分析

以18 相直驱永磁同步发电机的6 套三相绕组中的1 套为例，可以等效为1 个三相电压源(ua、ub、uc) 与定子电感Ls和定子电阻Rs串联，如图2所示。图中，右边为三相桥式不控整流电路，其整流输出经滤波电容C滤波后与负载R相连，Io为流经负载的电流，Uo为负载两端电压。

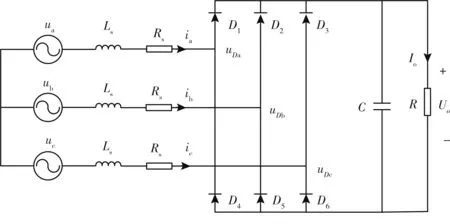
图2 三相桥式不控整流器

忽略定子电阻Rs和二极管正向导通压降可得定子电感上的压降为:

式中，ω为风机的电角速度，uk(ωt) 为风机a、b、c 三相的相电压(k＝1，2，3)，可以表示为:

式中，UL为风机线电压幅值，与风机机械转速ωm存在一定比例关系，具体为:

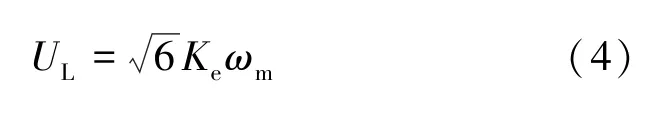
式中，Ke为电枢常数。

式(2) 中，uDk(ωt) 为三相桥式不控整流器的输入电压，与Uo存在以下关系:

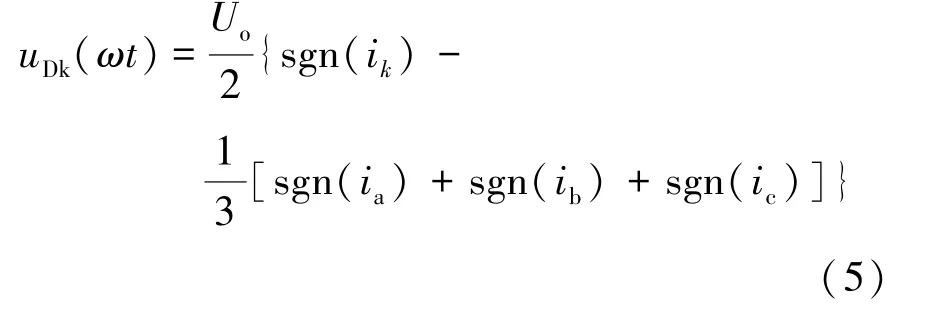
式中，sgn (x) 为符号函数:

图3 为三相桥式不控整流器交流侧三相电流波形，a 相电流ia(ωt) 的第一个上升过零点对应的相位为θ。

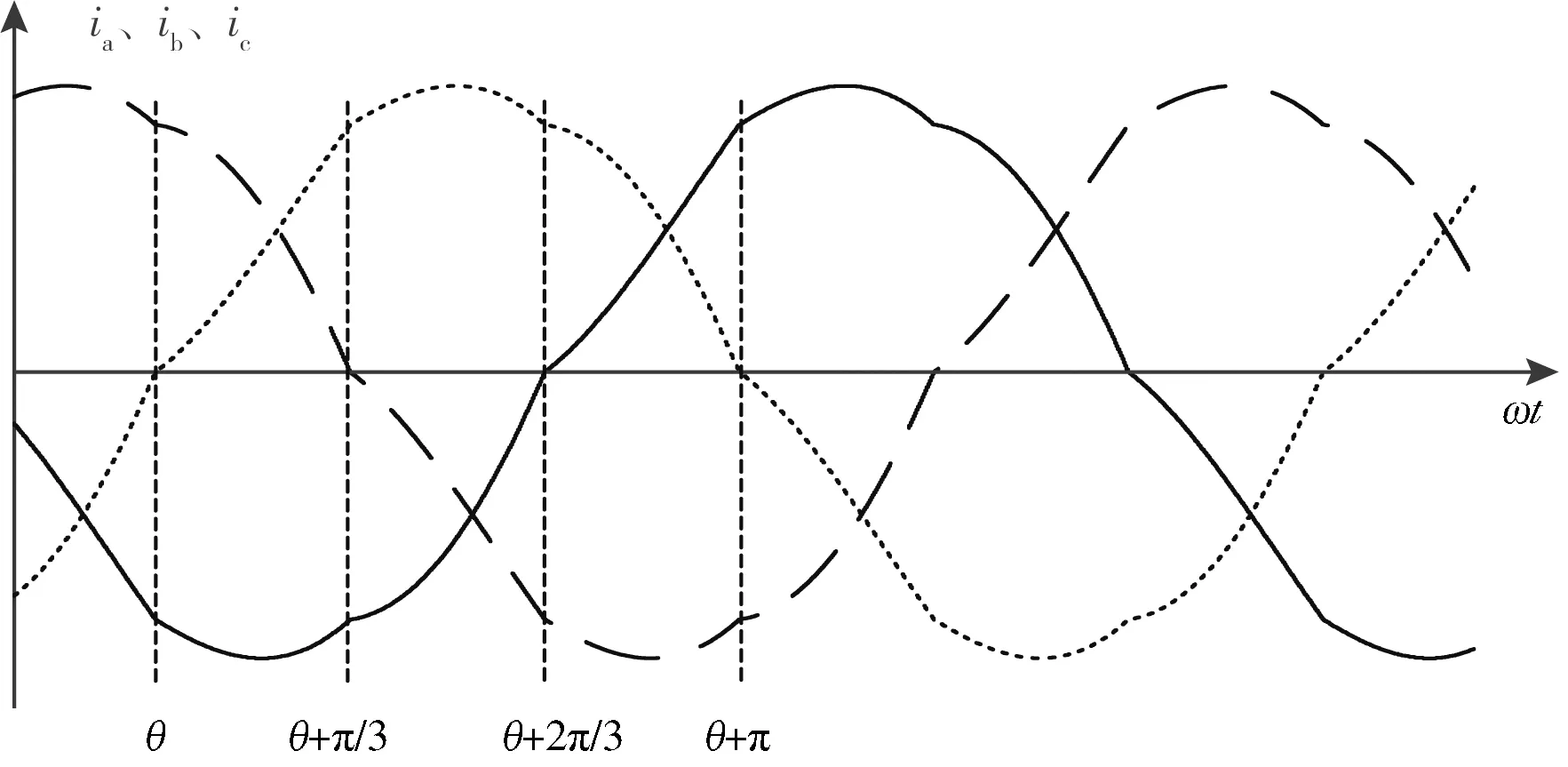
图3 三相桥式不控整流器输入电流

因此，uDa(ωt) 又可以表示为:

根据式(2) 可得机侧a 相电流半个周期后ia(θ＋π)的表达式为:

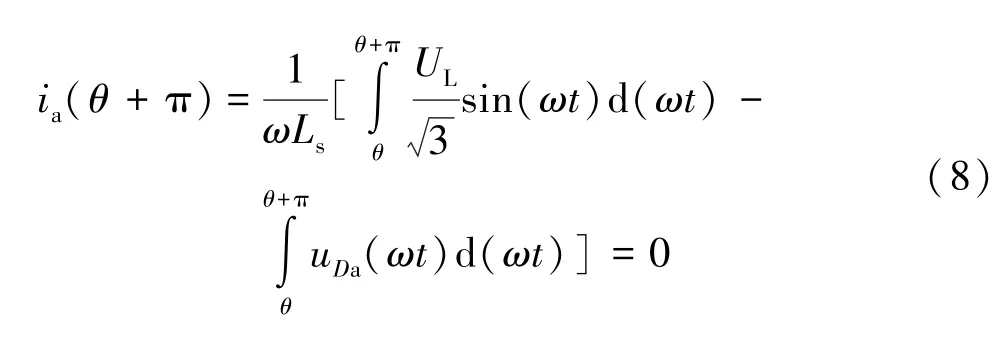
将式(7) 代入式(8) 可以得出:

2.2 计算三个阶段a 相电流值

第一个阶段为θ≤ωt<θ＋π/3，根据式(7) 可知，此时uDa(ωt) ＝Uo/3。再根据式(2) 可得第一阶段a 相电流值ia1(ωt) 为:

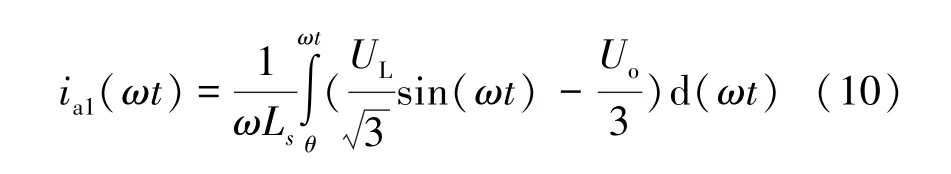
将式(9) 代入可得:

第二个阶段为θ＋π/3≤ωt<θ＋2π/3，根据式(7) 可知，此时uDa(ωt) ＝2Uo/3，再根据式(2) 可得第二阶段a 相电流值ia2(ωt) 为:

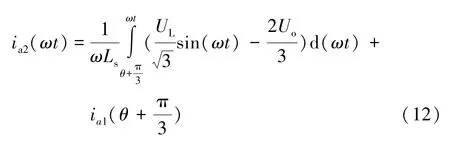
需要说明的是，此处ia1(θ＋π/3) 为第二阶段的初始状态。将式(9) 代入可得:

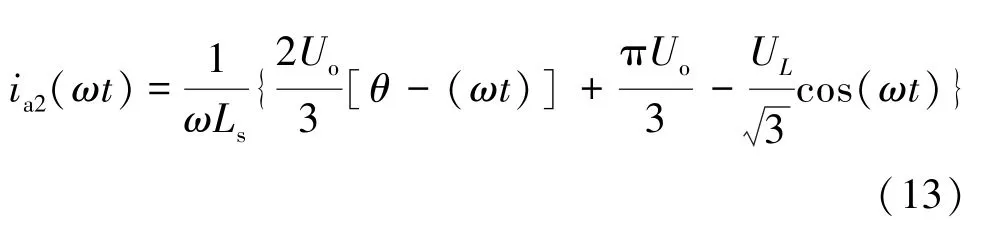
第三个阶段为θ＋2π/3 ≤ωt≤θ＋π，根据式(7) 可知，此时uDa(ωt) ＝Uo/3，再根据式(2)可得第三阶段a 相电流值ia3(ωt) 为:

求解式(14) 可得:

2.3 计算三相桥式不控整流器的输出电流

三相桥式不控整流器的输出电流Io满足以下关系:

根据对称性原理可以化简为:

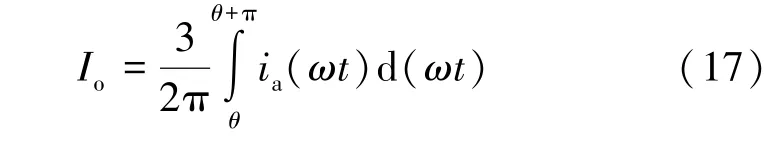
根据计算得到的三个阶段机侧a 相电流值，Io又可以计算为:

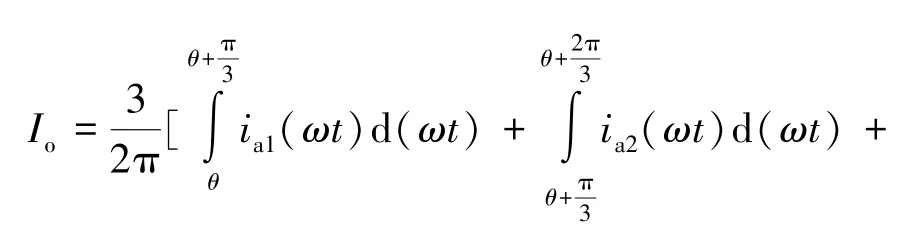
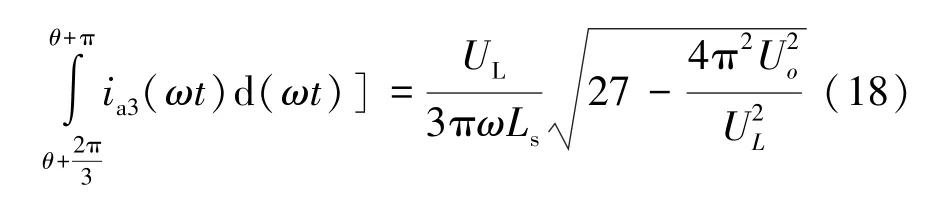
式(18) 描述了三相桥式不控整流器输出电流与输出电压之间的关系。

2.4 计算三相桥式不控整流器的输出功率

三相桥式不控整流器的输出功率Po为输出电压和输出电流的乘积，具体为:

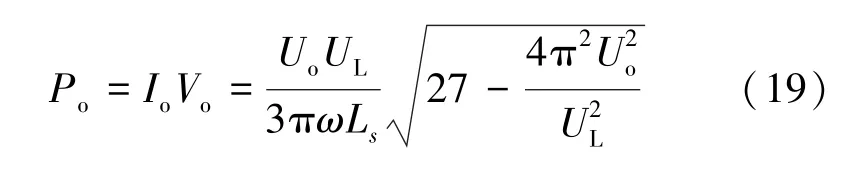
若要实现最大功率跟踪，需要实时跟踪Po的最大值Pomax，当达到最大功率点时，输出电压为:

将式(21) 代入式(19) 可得最大功率点的输出电流为:

由于ω与ωm存在以下关系:

式中，P为18 直驱相永磁同步电机的极数，将式(4) 和式(23) 代入式(19) 可得:

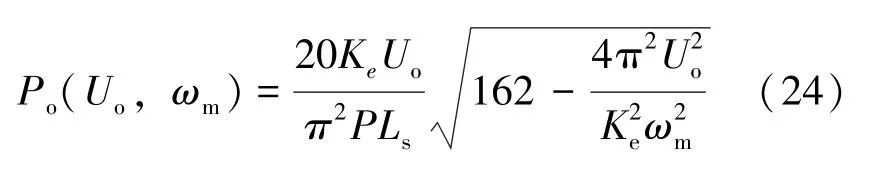
与上面相同，对Uo进行求偏导后可以计算出最大功率点时的三桥式不控整流器的输出电压和输出电流分别为:

显然，从式(26) 可以看出，当Po达到最大值时，Io为一固定值，即Io(Pomax) 与转速无关；只与18 相直驱永磁同步发电机的参数有关；由于参数已知，因此只需控制Io(Pomax) 稳定，即可实现最大功率跟踪。

2.5 隔离型H 桥DC/DC 变流器控制

考虑到实际运行中每套三相绕组对应的N个MMC 半桥子模块电容电压之间存在偏差，为减小该偏差，在保证DC/DC 变流器总输入电流恒定的条件下，基于电容电压进行充电电流分配，即端电压较低的电容分配较大的充电电流，反之分配较小的充电电流。电流分配规律满足下式所示:

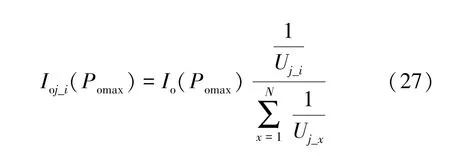
式中，Ioj＿i(Pomax) (i＝1，2，…N；j＝1，2，…6)为最大功率点时第j套三相绕组第i个并联DC/DC变流器的输入电流；Uj＿i为第j套三相绕组对应的第i个MMC 半桥子模块的电容电压。

将每个DC/DC 变流器的输入电流直流量Ioj＿i(measure) 与参考值Ioj＿i(Pomax) 作比较，然后经过PI 调节器，即可得到第j套绕组所对应的第i个DC/DC 变流器的占空比Dj＿i:

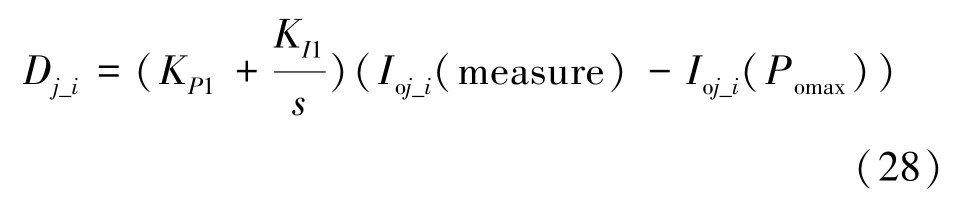
式中，KP1和KI1分别为第一个PI 调节器的比例系数和积分系数。图4 为最大功率跟踪控制框图。

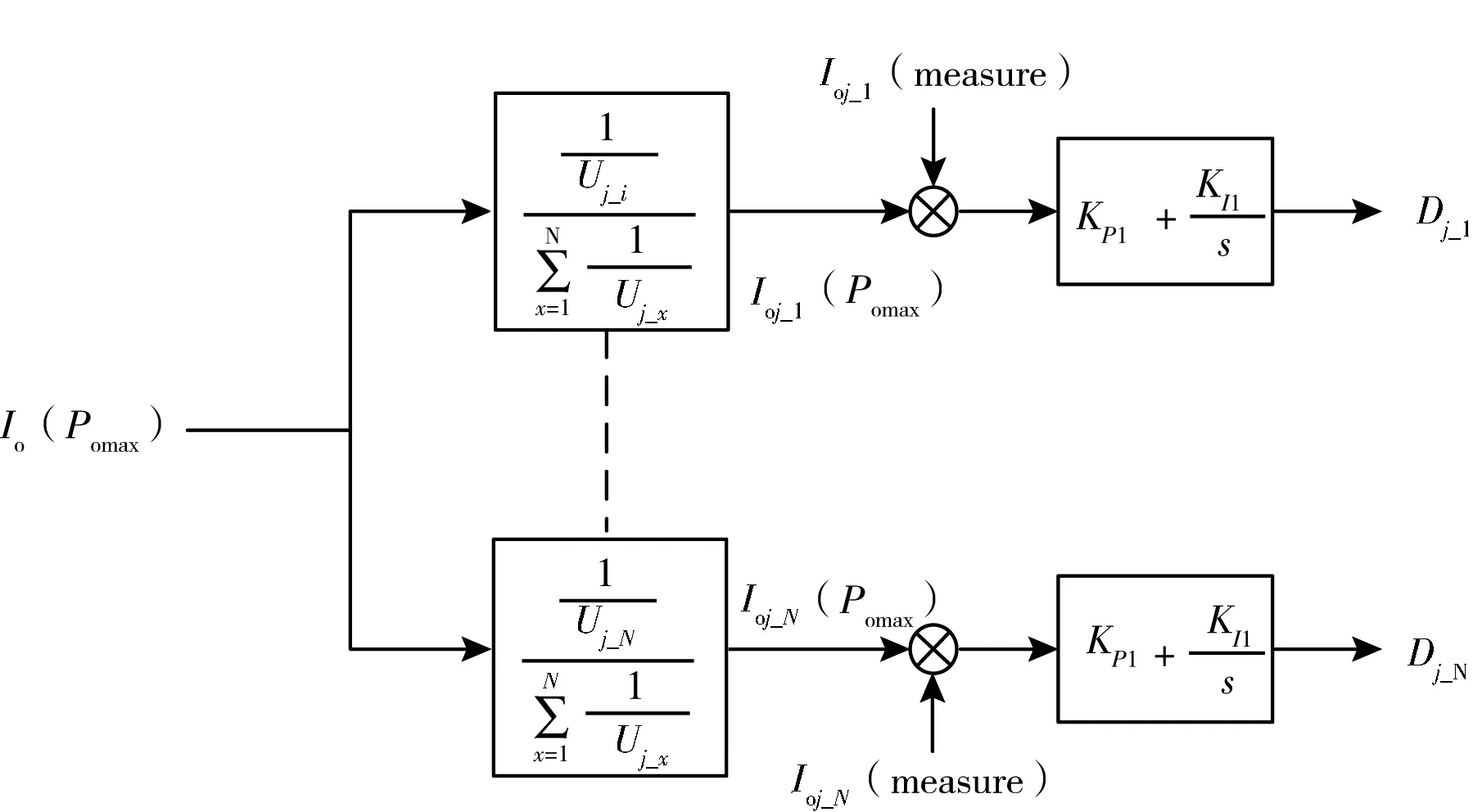
图4 最大功率跟踪控制框图

3 仿真分析

为了验证所提控制方法的正确性和可行性，在Matlab/simulink 中进行了仿真分析，系统仿真参数见表1。

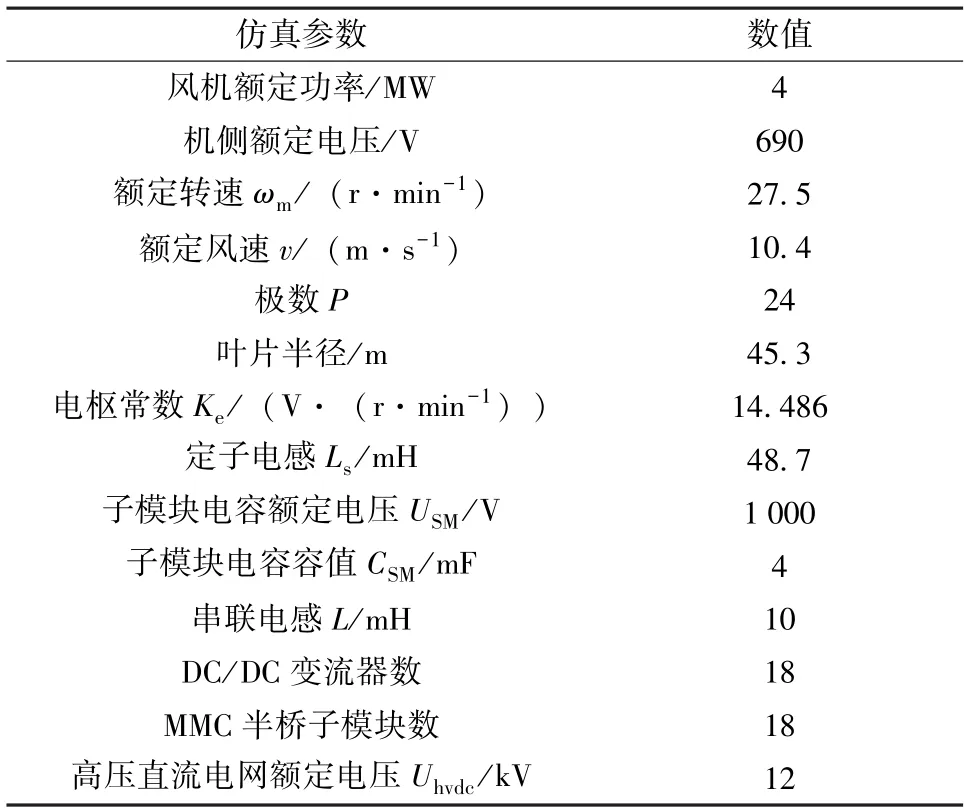
表1 系统仿真参数

3.1 额定风速下工况

在额定风速10.4 m/s 的情况下，仿真结果如图5 所示。

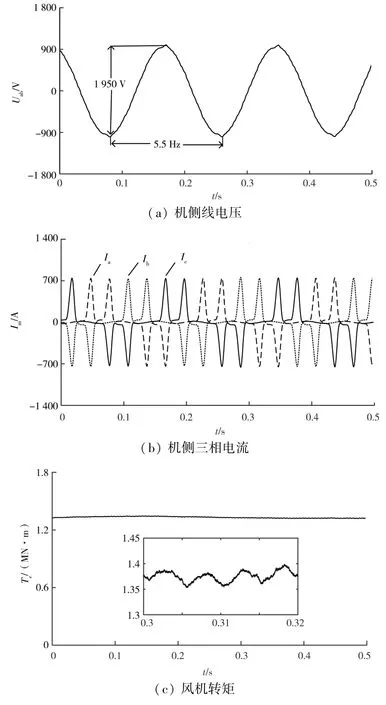
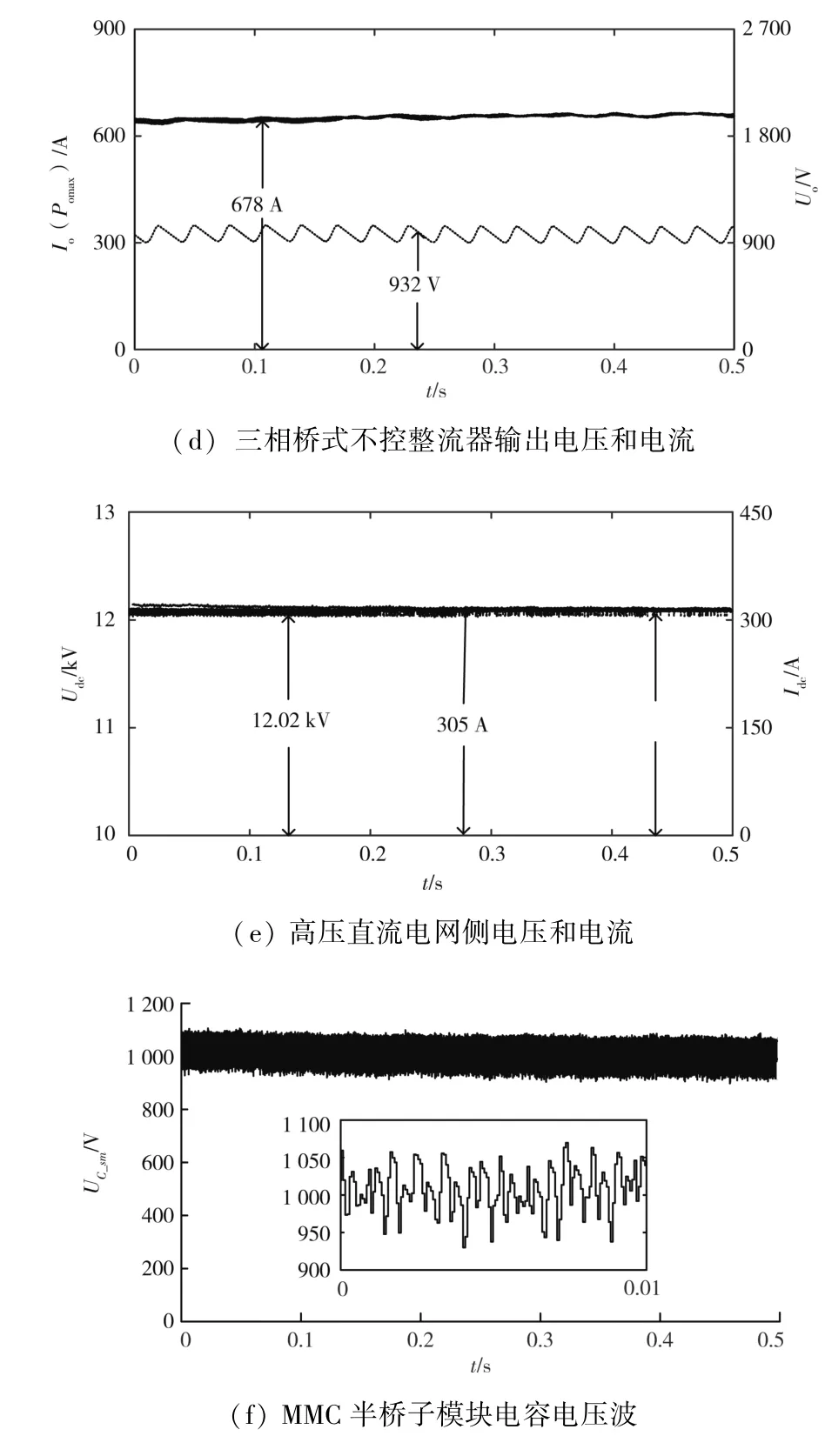
图5 额定工况下仿真结果

图5 (a) 为18 直驱相永磁同步发电机的线电压波形，满足正弦规律且谐波含量较低，幅值约为975.5 V，有效值约为690 V，基波频率为5.5 Hz。图5 (b)、5 (c) 分别为18 相电机的1 套三相绕组的定子电流和输出转矩波形。1 套三相绕组中，定子电流谐波成分主要为5、7 次谐波，但最后风机的输出转矩脉动较低，这是由于多相风机多套绕组定子电流进行叠加，从而谐波含量较低，体现多相风机的优势。图5 (d) 为最大功率点时18 相直驱永磁同步发电机一套三相绕组所连接的三相桥式不控整流器的输出电流和输出电压，输出电流基本稳定在678 A 左右，输出电压直流量基本稳定在932 V 左右，含有较小的纹波。

如图5 (e) 所示，高压直流电网侧并网电压维持在12.02 kV 到12.03 kV 之间，考虑到线路中的各种损耗，因而比额定值12 kV 略高；其波形为阶跃形式，因为投入的MMC 半桥子模块个数在12和13 之间跳变。当并网电流高于参考值时，就会导通13 个子模块来降低并网电流；当并网电流小于参考值时，就会导通12 个子模块来增加并网电流。考虑到电流变化时的电感EMF，导通13 个子模块时，并网电压会略低于这13 个子模块电容电压之和，导通12 个子模块时，并网电压会略高于这12 个子模块电容电压之和。高压直流电网侧并网电流，在额定工况下，其值基本为一恒定值，稳定在305 A 左右。

图5 (f) 为MMC 半桥子模块电容电压波形，电容电压有5%左右的轻微波动，这也是能量传输的根本原因。当电容电压大于额定值时，子模块将会在下一个控制周期导通，将能量传输给电网。

3.2 风速波动下工况

在0.1 s 时，风速由额定风速下降到8 m/s，其仿真结果如图6 所示。

图6 风速波动下仿真结果

图6 (a) 为18 相直驱永磁同步发电机的线电压波形，风速变化后，幅值由975.5 V 下降到620 V，即线电压由690 V 下降到438 V，基波频率也由5.5 Hz 下降到3.5 Hz。图6 (b)、6 (c) 分别为1 套三相绕组的定子三相电流和电机的输出转矩，风速变化后，定子电流基波幅值有所下降，通过多相绕组叠加消除之后，仍能得到较为稳定的输出转矩。图6 (d) 为风速变化后最大功率点对应的三相桥式不控整流器的输出电流和输出电压，电流从678 A 下降到670 A 左右，有轻微波动，可忽略不计；输出电压从932 V 下降到539 V 左右。

图6 (e) 为高压直流电网侧并网电流和并网电压，风速变化后，Idc从315 A 下降到171 A，这是因为永磁同步发电机的输出功率随风速降低会相应减小；并网电压仍维持在12.01 kV 到12.02 kV之间。暂态过程中，投入12 个MMC 半桥子模块的情况出现得较多，因为并网电流存在下降趋势。图6 (f) 为风速变化后MMC 半桥子模块电容电压，风速下降后，子模块电容电压波动有所减小。

4 结论

风力发电技术和高压直流输电技术广泛应用，而将大功率多相风机应用于风力发电却鲜有研究。本文采用18 相直驱永磁同步发电机经三相桥式不控整流器和隔离型H 桥DC/DC 变流器并入高压直流电网的拓扑结构，并提出一种新的最大功率跟踪控制方法，通过一系列理论推导得出最大功率点所对应的三相桥式不控整流器的输出电流为一恒定值这一结论。与传统的爬山搜索法和功率信号反馈法相比，所提控制方法大大减小了控制复杂度，最后通过仿真验证所提控制方法的正确性和有效性。为拓展所提控制方法适用情况，笔者实验室将对其展开进行进一步研究。