基于主成分分析法的变压器直流偏磁声学异常检测
2022-01-06曹浩黄韬周舟解杰
曹浩,黄韬,周舟,解杰
(1.国网湖南省电力有限公司电力科学研究院,湖南 长沙 410007;2.国网电力设施噪声与振动实验室,湖南 长沙 410007;3.华北电力大学电气与电子工程学院,北京 102206)
0 引言
变压器作为电力系统最重要的设备之一,对电力系统安全可靠运行十分重要[1]。基于声学信号在线监测不会对变压器的安全稳定运行产生干扰[2],且声学信号中包含的信息可以反映变压器工作状态和异常情况[3-4]。由于变压器所在环境易受到各种噪声影响,影响测量的声学信号,从而导致故障诊断的准确率下降[5]。变压器声纹信号的去噪和特征提取是故障诊断的前提[6],滤除噪声信号对变压器故障在线监测具有重要意义[7-8]。利用数据驱动方法中的无监督、半监督机器学习方法将采集到的声学信号检测变压器的运行状态[9],对变压器这种结构复杂的对象无需构建物理模型,具有更高的可行性。
1 小波阈值法去噪
1.1 小波变换
小波变换可以反映信号的局部特征,通过改变窗函数,在低频信号处窗函数较宽,而在高频信号处窗函数较窄,相对于傅里叶变换和短时傅里叶变换具有更广阔的应用前景[8]。
1.1.1 连续小波变换
设ψ(t) ∈L2(R),其傅里叶变换为ψ(ω) 。当ψ(ω) 满足式(1) 时,称ψ(t) 为小波基。
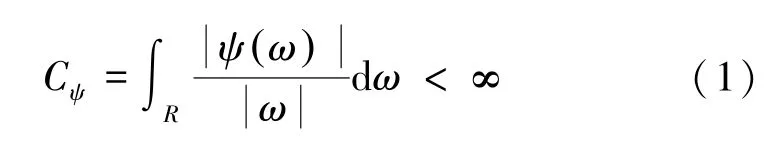
对ψ(t) 平移伸缩变换得到:
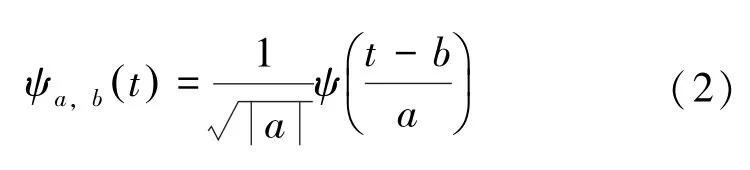
式(2) 为一个新的小波序列,其中,a为尺度因子,b为平移因子,a,b∈R;a≠0。对于任意函数F(t) ∈L2(R) 的连续小波变换为:
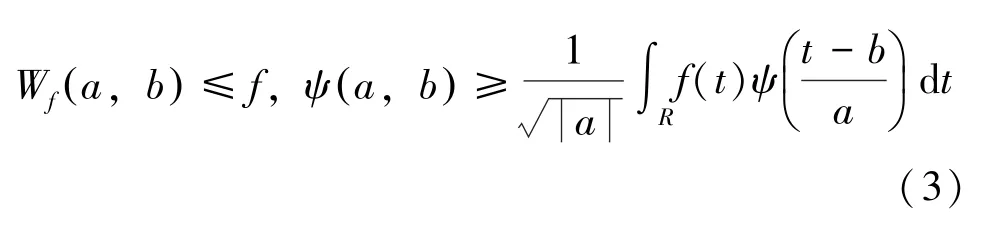
连续小波的重构,即连续小波的逆变换为:

1.1.2 离散小波变换
离散小波变换是为了使连续的尺度因子a和平移因子b离散化。在离散过程中,令尺度因子a始终取正值,则容许性条件为:
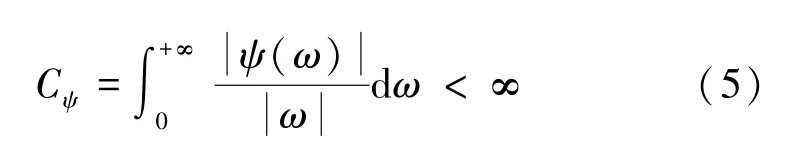
对尺度因子a和平移因子b进行离散化:

式中,m、n∈Z,a0为不等于1 的固定值。
1.2 小波去噪原理
记含有噪声的信号s(n) 表达式为:
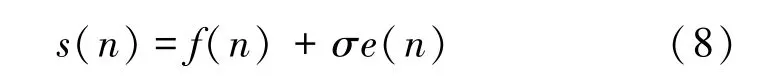
式中,f(n) 为原始信号,σ为噪声水平,e(n) 为噪声。
去噪就是将式(8) 原始信号中σe(n) 滤除的过程。利用小波变换去噪的方法主要有:小波模极大值去噪算法、小波阈值去噪算法、小波空域相关去噪算法。表1 为上述几种去噪算法的比较。
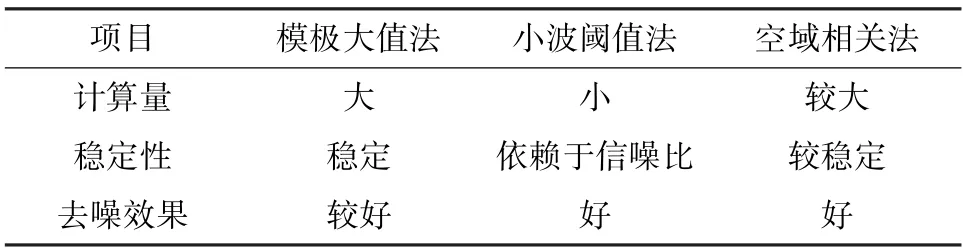
表1 不同小波变换法去噪的定性比较
由表1 可以看出,小波阈值去噪算法计算量小、去噪效果好,更具有应用价值。
小波阈值去噪算法理论认为,噪声的小波系数通常小于信号的小波系数,通过设置不同尺度的阈值函数,滤除低于阈值的小波系数,达到去噪的目的[10]。
1.3 实测信号去噪
在北京市某变电站录制了嘈杂环境下变压器声音信号,利用Matlab 仿真软件完成实验。采用阈值,其中,σ为噪声标准差,N为信号长度,采用硬阈值函数作为小波阈值函数。小波基的选取缺乏系统的理论,综合考虑小波的光滑性、对称性、紧支撑性,选取Daubechies3 小波系,根据频率分解情况,层数选为4 层。
利用Matlab 软件,对实测变压器声音信号分析,原始信号的波形如图1 所示,频域图如图2 所示。利用上述小波阈值法去噪后的信号波形如图3所示,频域图如图4 所示。
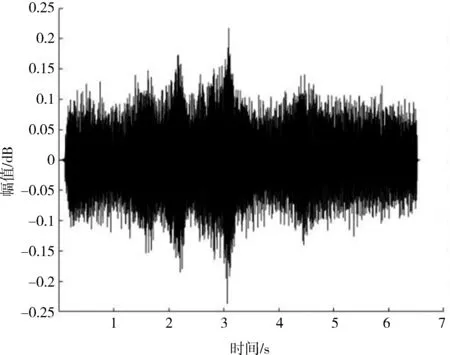
图1 变压器声学原始信号波形图
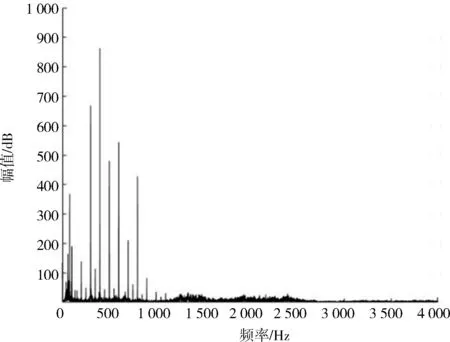
图2 变压器声学原始信号频域图
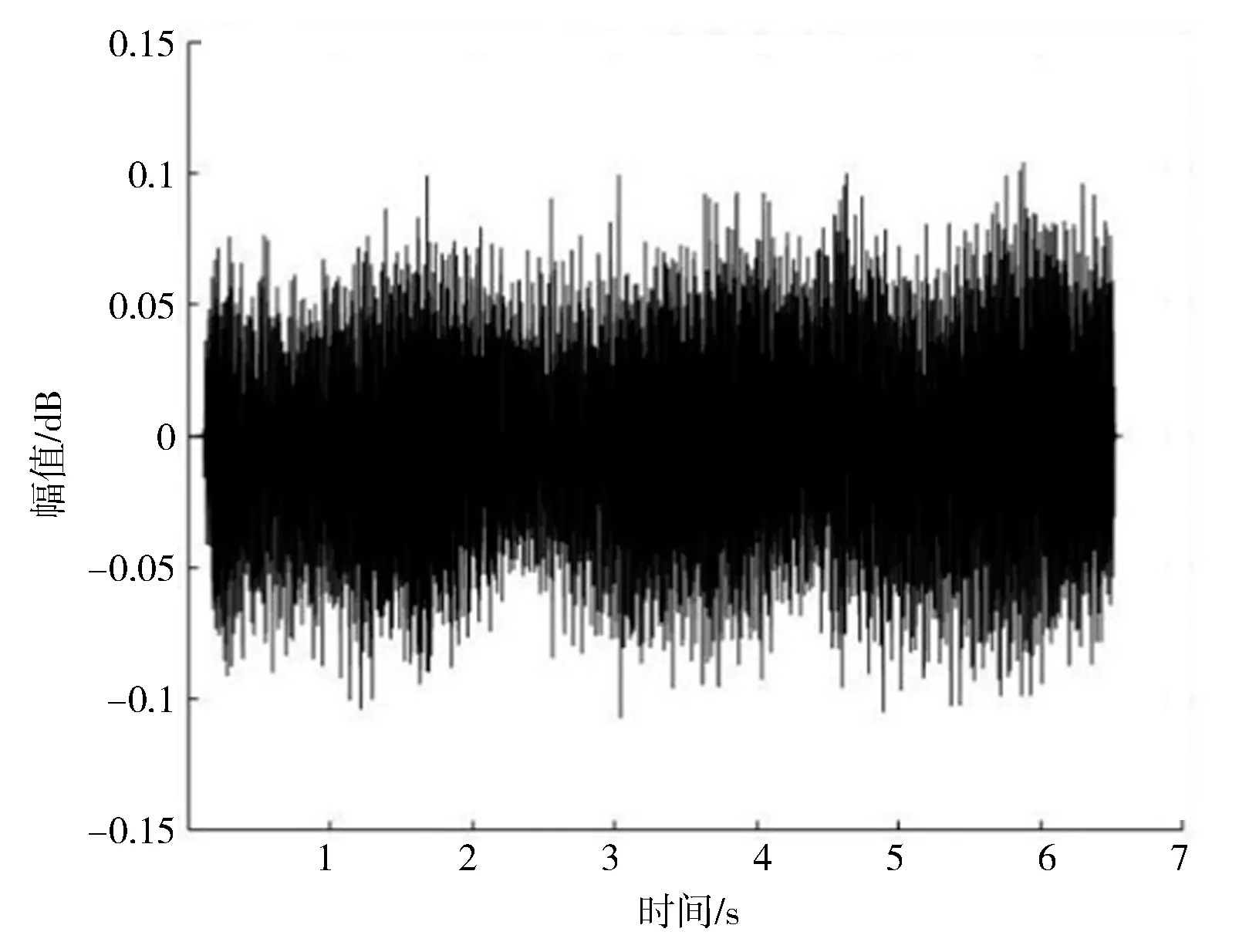
图3 去噪后变压器声学信号波形图
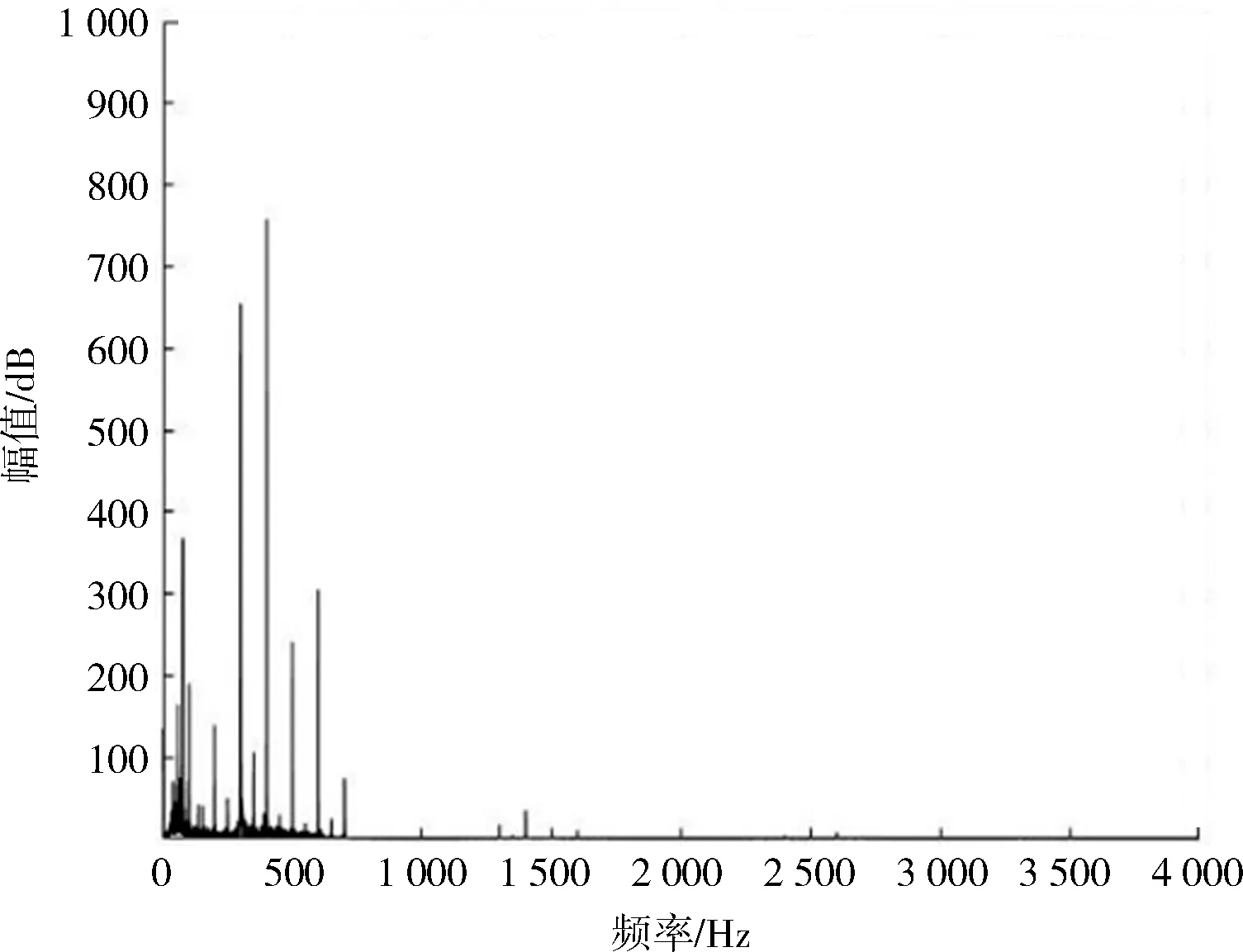
图4 去噪后变压器声学信号频域图
信号去噪前后对比得出小波阈值法对变压器声音信号具有较好的去噪效果。去噪后,滤除了原始信号中波动较大、不属于变压器本体发出的声音信号,滤波后信号更为平滑,频率段也更为集中,符合变压器声音的机理特征[6-17]。
2 梅尔频率倒谱系数
梅尔频率倒谱系数 (Mel-Frequency Cepstral Coefficients,MFCC) 是音频信号处理中常用的方法[16]。利用MFCC 进行特征提取,分为数据的预处理和MFCC 特征提取两部分[18]。
2.1 数据预处理
2.1.1 预加重
在音频信号中,信号能量通常集中在低频部分,然而功率谱随着音频信号频率的增加不断减小,这会导致信号高频部分的信噪比大幅下降。对信号预加重的目的是提高音频信号中的高频部分,有利于平衡频谱,改善信号整体信噪比。预加重实质是一个高通滤波器,其表达式如下:
式中,α为滤波器系数,取值通常为0.95~0.97。
2.1.2 分帧
变压器音频信号具有短时平稳性,即变压器音频信号在整体上是连续变化的,将音频信号分割成一系列的短时帧,这样的音频信号是相对稳定的。通常设置短时帧的时间长度范围为20~40 ms,相邻短时帧有50%±10%的重叠率。这样既可以得到音频信号的频谱分辨率,又不影响音频信号的时不变性。
2.1.3 加窗
在音频信号的每一帧上,利用窗函数信号使信号向帧边界衰减,使得每帧的左右两端更加连续,在特征提取中减少频谱泄露的发生。常见的窗函数有矩形窗和汉明窗两种:
1) 矩形窗函数:

2) 汉明窗函数:
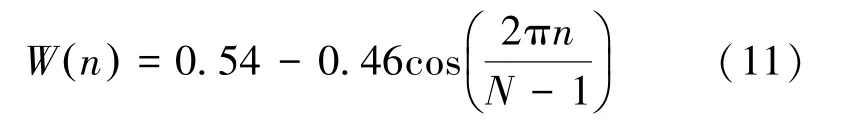
式中,0 ≤n≤N-1,N为窗长。
2.2 MFCC 特征提取
2.2.1 快速傅里叶变换
短时帧信号在加窗处理后,还必须进行一次快速傅里叶变换,得到信号在频域中的分布情况,对信号的频谱取模的平方即可得到信号的谱线能量。
2.2.2 梅尔频谱
将经过快速傅里叶变换后的信号通过梅尔滤波器组计算得到梅尔频谱[12]。滤波器组均用三角形,其传递函数为:
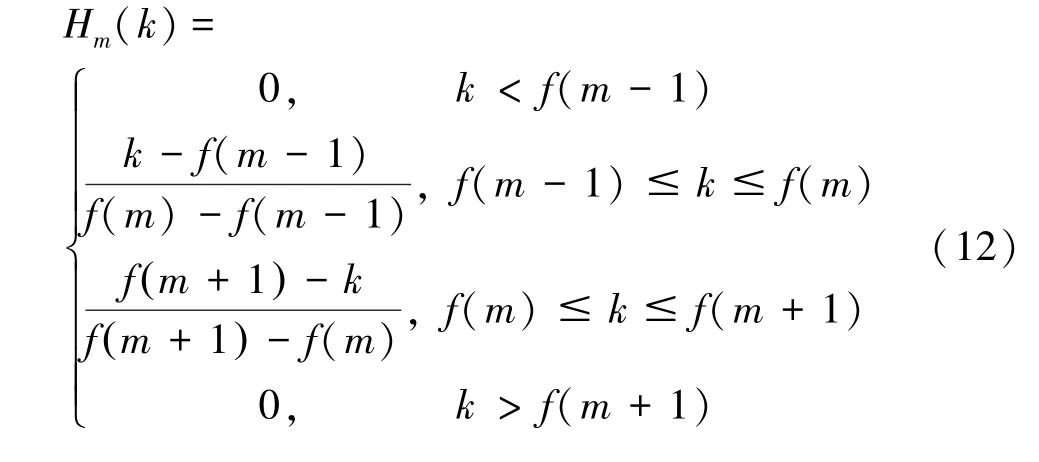
在中心频率处的响应为1,并向两边线性减小,达到相邻两组滤波器中心频率时减为0,如图5 所示。信号通过三角梅尔滤波器组频谱变得更为平滑,可以有效消除谐波,凸显原始信号中的共振峰。
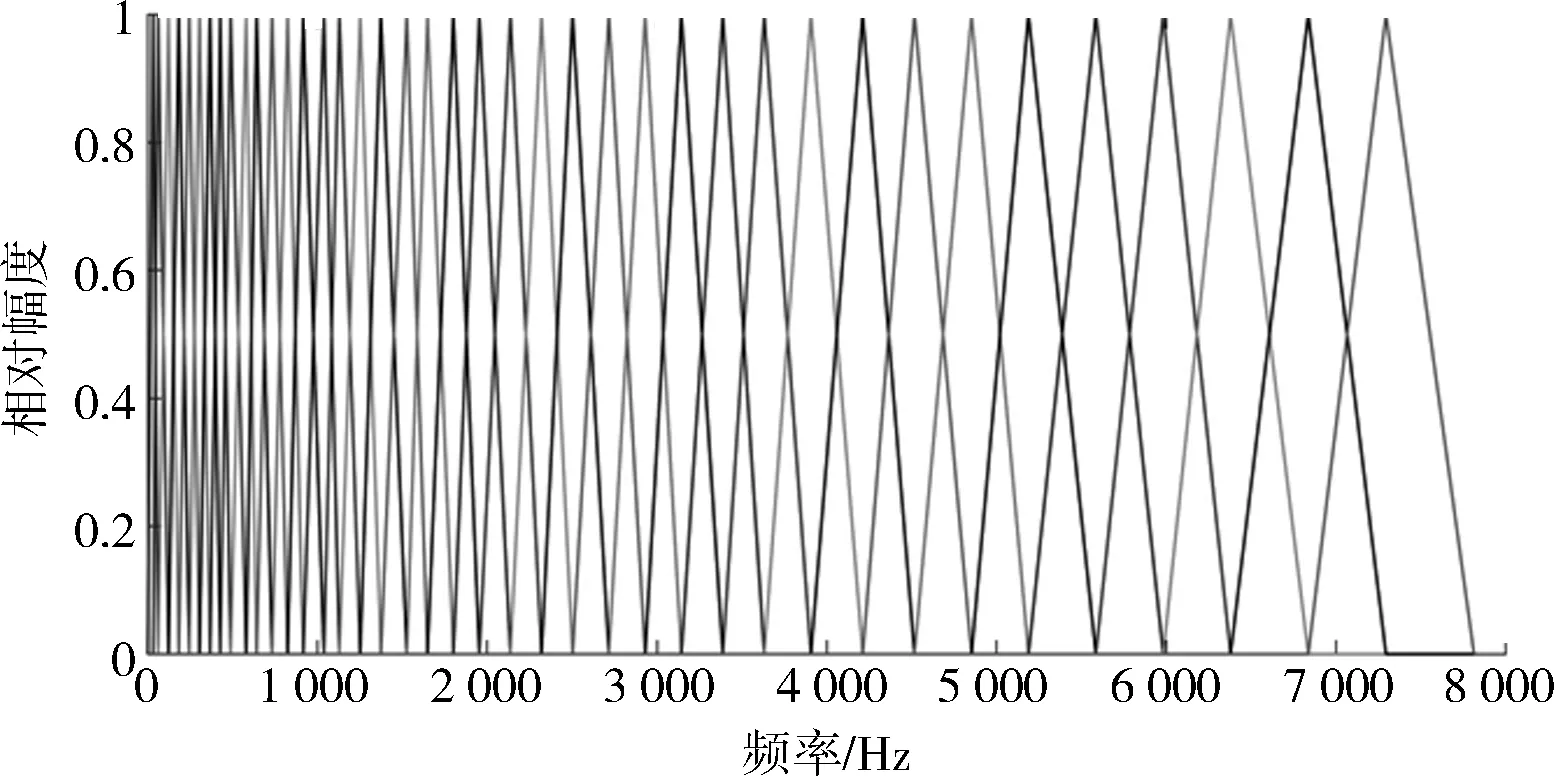
图5 梅尔滤波器组
2.2.3 离散余弦变换
在进行离散余弦变换(DCT) 之前,梅尔频谱常用对数尺度表示,对数梅尔频谱经离散余弦变换(DCT) 转换成一组梅尔频率倒谱系数。MFCC 计算公式为:

式中,C(n) 为倒谱系数,C为MFCCs 数量。
3 实测数据故障检测
3.1 变压器实测声音
采集到北京某变电站变压器(110 kV) 正常工况和直流偏磁工况下声音数据。正常运行时,信号的时域图、频域图和频谱图[19]如图6、图7、图8 所示。
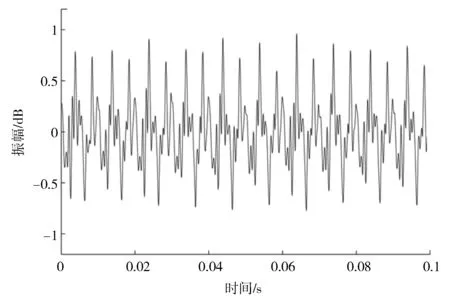
图6 正常工况信号波形图

图7 正常工况信号频域图

图8 正常工况信号频谱图
直流偏磁工况下,信号的时域图、频域图和频谱图如图9、图10 和图11 所示。
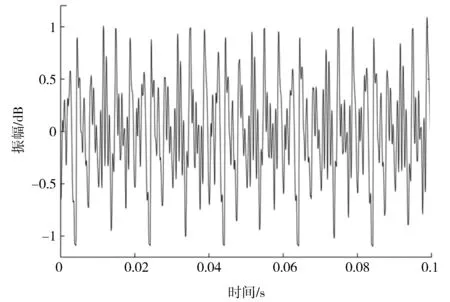
图9 直流偏磁工况下信号波形图
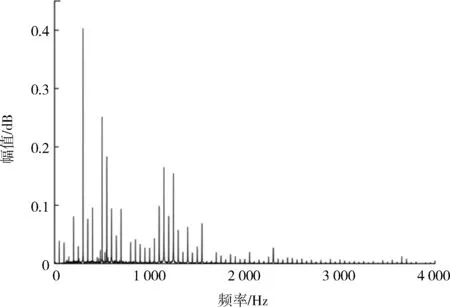
图10 直流偏磁工况下频域图

图11 直流偏磁工况下频谱图
3.2 MFCC 特征提取
分别对正常数据和直流偏磁数据用上文提供的方法去噪、特征提取,得到不同工况下声音信号的MFCC 特征,如图12 和图13 所示。

图12 正常工况信号MFCC 特征

图13 直流偏磁故障下MFCC 特征
4 变压器声学异常检测
4.1 主成分分析法
主成分分析法是一种能有效降低算法的计算开销,使得数据集更易使用的数据降维方法,将多维特征映射到维度较小的一组线性无关的正交向量中。主成分分析中经过特征值分解得到特征向量反映了原始数据在不同方向的方差变化情况,体现了原始数据的内在规律。当个别数据样本与整体数据样本表现的特征出入较大,则可认为该数据样本为异常。通过计算数据点到每一个主成分方向质心的归一化距离实现,记ej为第j个特征向量,对应的方差为λj。信号数据点到数据中心λj的异常程度由下式给出:
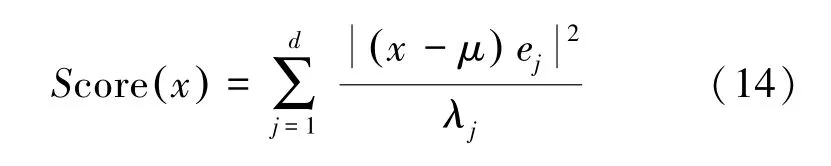
计算n维数据矩阵D的异常情况计算方法如下:计算原始数据矩阵D的协方差矩阵Σ,并将其对角化Σ=PΔPT;将矩阵D转换成一个线性无关的坐标系,D′=DP;将矩阵D′的每一列与其标准差相除,转为标准单位方差;对矩阵D′每一行,计算其距离矩阵D′中心位置的欧式距离作为异常分值。
4.2 机器学习异常检测
利用主成分分析法对正常和异常(直流偏磁)变压器数据进行异常检测,使用机器学习中无监督方法和半监督方法进行训练[13]。无监督方法的数据无标签,含有少部分异常数据。半监督方法的训练集只包含正常数据,利用正常数据训练出检测模型,不符合模型的数据都认定为异常数据[14]。为方便展示检测效果,选用了MFCC 特征的第6 维和第9 维进行异常检测,主成分分析法异常检测结果如图14、15 所示,图中白点表示正常数据,黑点表示异常数据。

图14 无监督学习检测结果
从检测结果可以看出,主成分法的决策边界为椭圆形,半监督方法相对于无监督方法具有更高的异常数据检测、区分能力。
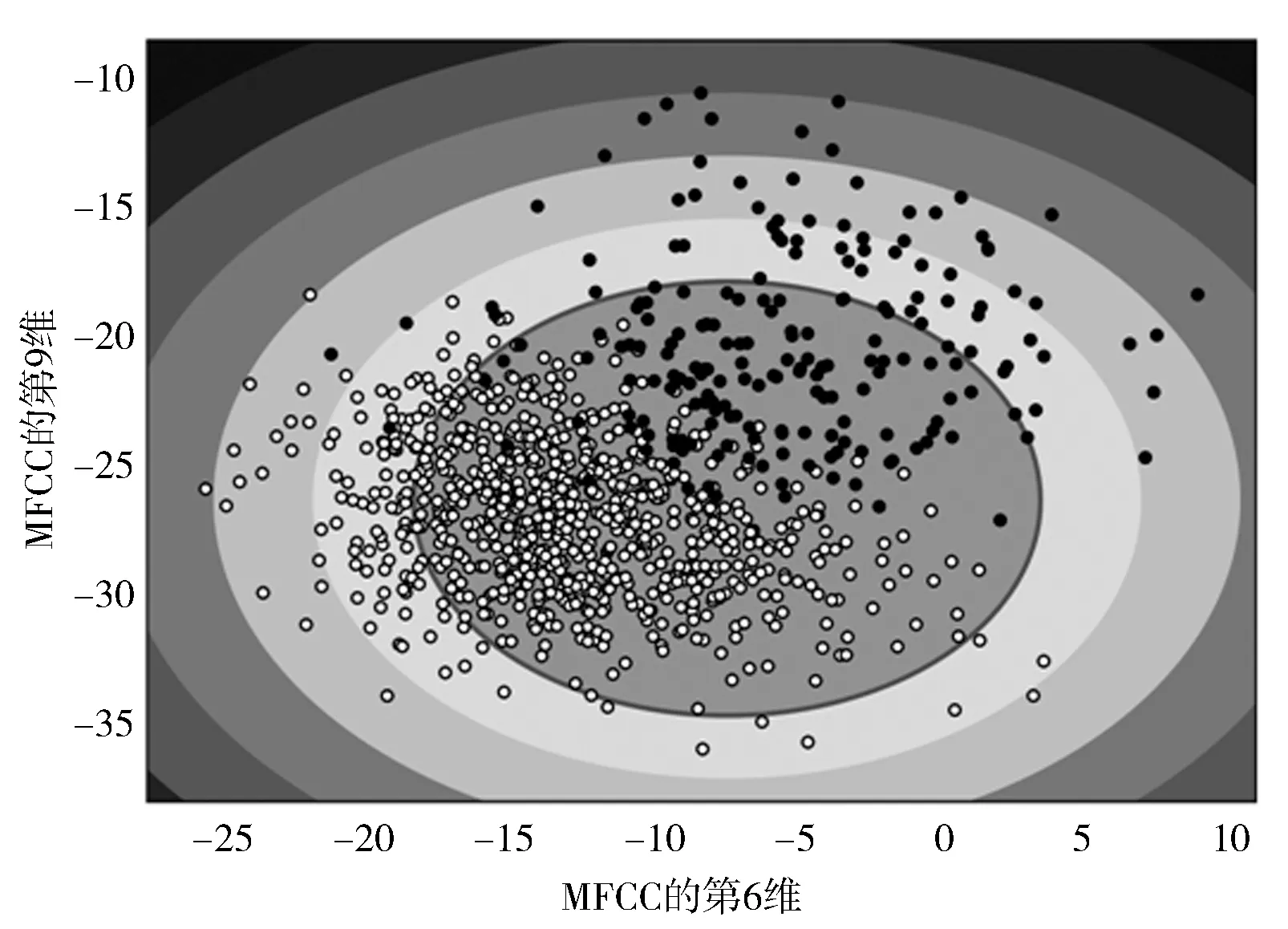
图15 半监督学习测结果
为进一步定量比较无监督方法和半监督方法的检测能力,将变压器声音信号1 s 分为1 组,共分1 000 组,其中800 组为正常数据,200 组为异常数据。利用MFCC 特征提取方法提取1 000 组MFCC 特征并进行异常检测,每组MFCC 维度为40维。使用主成分分析法,进行训练和测试,训练模式分别采用无监督方法和半监督方法。主成分分析检测算法在MFCC 特征上的AUC 见表2。
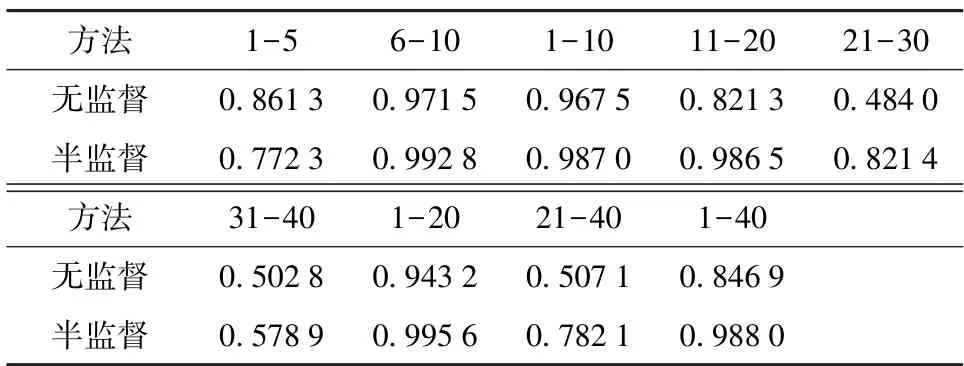
表2 主成分分析法在MFCC 特征上的AUC
从表2 可以看出,无监督方法在6—10 维的MFCC 特征检测效果最好,1—10 维的检测效果次之,在21—30 维检测效果最差;半监督方法在1—20 维的MFCC 特征检测效果最好,6—10 维检测效果次之,在31—40 维度检测效果最差。整体来看,半监督方法比无监督方法具有更好的检测效果。
5 结论
以北京市某110 kV 变电站变压器正常运行和直流偏磁工况下的声音数据为研究对象,对信号去噪、特征提取,利用主成分分析法通过无监督和半监督模式进行变压器声学异常检测,得出以下结论:
1) 变压器正常运行时声音信号频率集中在0~2 000 Hz。其中50 Hz 偶数倍频分量较高,并伴有一些50 Hz 的奇次倍频分量。
2) 使用无监督和半监督异常检测方法解决变压器异常数据稀少问题。
3) 通过实测数据测试表明,半监督学习算法较无监督学习算法具有更高的检测效果。
4) 由于采集到的异常数据类型有限,下一步将采集更多类型的异常数据,建立适应的诊断模型,实现故障类型的判别。
