光伏建筑一体化行业板块指数的预测模型构建——基于ARIMA模型的实证分析

宋怡梦， 陈星池

(1.暨南大学 国际商学院， 广东 珠海 519070; 2.暨南大学 智能科学与工程学院， 广东 珠海 519070)

随着全球气候变暖问题越来越受到国际社会的关注，碳减排已经成为国际重要议题。为了积极地应对气候变化，中国计划在2030年前达到“碳峰值”，在2060年前实现“碳中和”的目标。而光伏建筑一体化是一种能将太阳能发电产品集成到建筑上的技术[1]，该技术以具有能够有效降低建筑用能，大力发展低碳、零碳建筑的特点，成为降碳节能的重要解决方案。这无疑说明，在30、60双碳目标之下，光伏建筑一体化行业在面临新的挑战的同时，也将会迎来更多的投资机会。

在这样的背景下，当今国内光伏建筑一体化行业已经迈入了加速发展期，也吸引了较多的上市公司参与其中。而股票交易市场中的板块指数是将同一板块的个股按不同的权重方式生成相关指数，它是对该行业板块走势的整体反映[2]。基于此，对与光伏建筑一体化板块指数涨跌趋势有关因素的预测研究，是把握该行业未来发展趋势的重要方法。

近些年来国内外学者使用各种各样的方法进行股票的预测研究，也提出了多种股票预测模型。然而，之前关于股票市场预测的研究，大多数并未聚焦于板块，而是以大盘指数作为主要研究对象，如上证指数、深圳综指等[3]。针对此理论缺口，当下急需适合的数学模型对股票市场板块指数预测研究[4]。而国外学者Idrees等曾通过分析印度股票市场的时间序列数据，建立了ARIMA预测模型，并得出ARIMA模型能够有效预测未来股票趋势的结论，并且将得到的模型通过了ADF 检验和 L-Jung-Box 检验[5]。

在这样的背景下，考虑到光伏建筑一体化作为一个新兴发展的板块，从未有相关学者专门对其市场发展趋势进行预测研究。故本文利用2019年4月1日至2021年5月28日沪深股市中 37 家光伏建筑一体化相关企业的股票数据，建立差分自回归移动平均模型(即ARIMA模型)对光伏建筑一体化的板块指数发展趋势做出预测，以弥补关于光伏建筑一体化行业上市公司研究的不足的同时，帮助市场投资者和企业管理者更好地把握光伏建筑一体化行业未来的发展趋势。

1 光伏建筑一体化板块指数发展现状

1.1 板块指数的计算

1)选取2019年4月1日至2021年5月28日沪深股市中 37 家光伏建筑一体化(BK0978)相关企业的股票数据，其数据来源于东方财富网。经过数据处理，筛选出光伏建筑一体化指数的开盘价、收盘价、最高价、最低价，共计19 425个样本数据，并根据这些数据采用派许加权方法逐一计算出该板块指数[6]，其公式为

(1)

式中：v为2019 年4月1日至 2021年5月28日该板块的调整市值，v=Σ(PNab)；I为指数符号；D为除数；BP为基点的大小，定为1 000点。未特殊说明时，权重因子a、汇率b均为1。

2)通过查询37家光伏建筑一体化相关上市公司股本结构的资料，可得各上市公司的样本总股本和流通股本数。对得到的样本总股本计算平均值，作为该企业的样本总股本n1。对得到的流通A股本和流通B股本取平均值并相加得到该企业自由流通量n2。采用分级靠档的方法对样本股本进行调整而获得调整股本数N，即根据自由流通量n2所占样本总股本n1的比例(即自由流通比例n3)赋予类别股份总股本一定的加权比例n，可以使得计算指数的股本保持相对稳定。

(2)

根据中证指数有限公司股票指数计算与维护细则中规定可知，n3确定指数样本的加权比列n，故得到调整股本数N最终的计算公式为

N=n1n

(3)

通过上述计算得到的调整股本数N，取每日各公司收盘价作为股票价格P，选取各公司每日收盘价为股票价格P，通过MATLAB计算得到调整市值V。

3)以基日股票调整市值为基值，即按照各股票公司上市开始交易时的市值之和作为除数，按照上述计算调整市值V的方式，令股票价格为各公司收盘价，并通过MATLAB计算出除数D=1 837.824 2。

1.2 结果与分析

根据指数计算公式，将以上所得的数值代入，可以求解出2019 年4月1日至2021年4月30日该板块指数的散点图(图1)。

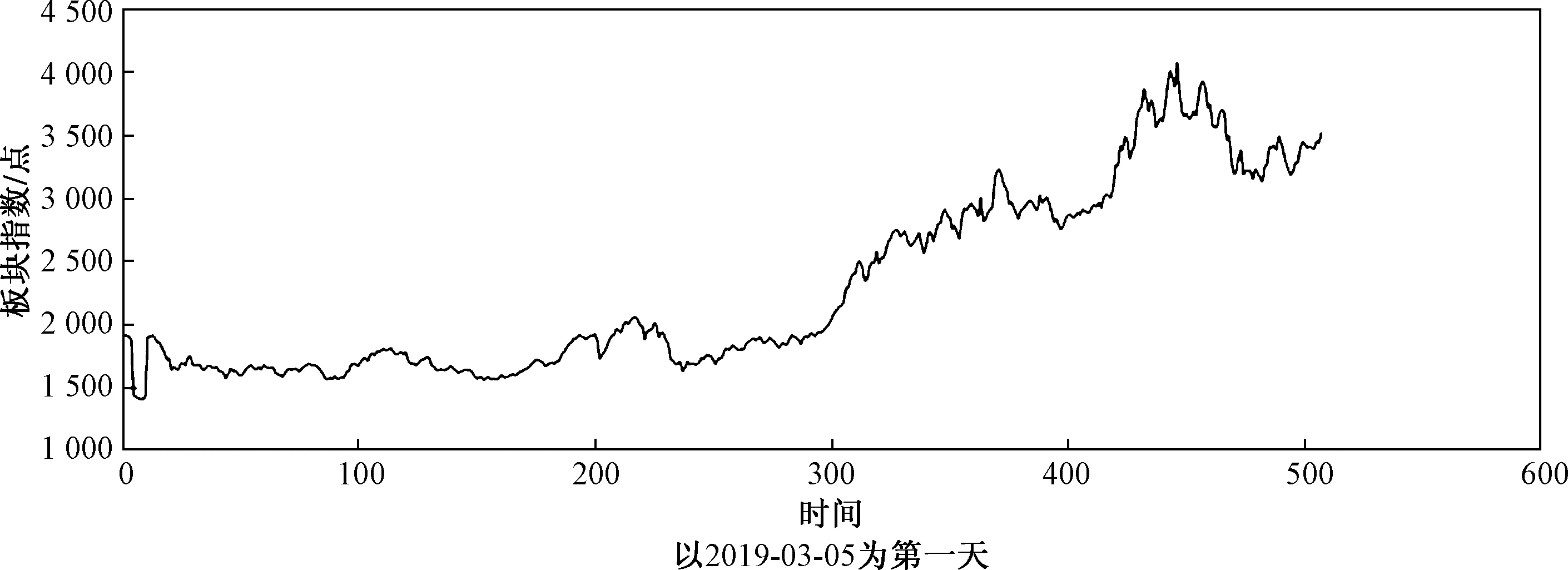
图1 光伏建筑一体化板块指数发展现状(2019-04-01至2021-04-30)

由图1可知，该行业在发展前期(在2020年之前)处于缓慢状态。中国光伏建筑一体化行业发展缓慢这些都与存在的一些瓶颈和缺陷有关，比如符合建筑多方面需求且成本较低的光伏组件产品较少，成本居高不下，投资回报周期长等[7]。

然而，随着中国光伏技术不断创新升级，各种新型的光伏建筑一体化技术不断涌现，尤其是以铜铟镓硒(CIGS)薄膜光伏组件、晶硅光伏组件、碲化镉薄膜光伏组件为代表的技术，给光伏建筑一体化行业带来了更多的发展空间。同时，自2021年以来该行业的发展有爆发迹象，而这背后离不开政策因素的驱动。2021年6月20日，国家能源局发布了《关于报送整县(市、区)屋顶分布式光伏开发试点方案的通知》，全国多地省市迅速颁布了相关政策。这些都无疑说明了在碳达峰、碳中和以及绿色低碳发展的目标下，光伏建筑一体化行业迎来了更多的新的挑战，也将会具有更多发展空间和投资机会。然而，仅仅从定性的角度去对光伏建筑一体化行业发展趋势进行预测无法保障投资者一定会获取收益，当下急需要建立相关的模型通过对光伏建筑一体化行业板块指数发展趋势进行分析，从而更加精确把握该行业的投资盈利点。

2 数据预处理与模型初步构建

2.1 数据预处理

根据上述所计算出的数值，代入公式得到2019年4月1日至2021年4月30日的板块指数数据，并通过Python画出的散点图(图2)。分析图2可知，该序列是非平稳的时间序列。为得到一个平稳的时间序列需进行时间序列的差分，则需要对其进行差分处理。

图2 指数散点时间点序列图

图3 对数据进行一阶差分后的时间点序列图

对数据进行一阶差分得图3。根据图3可知，一阶差分的时间序列的均值和方差已经基本平稳，故选择一阶差分对数据进行预处理。

2.2 ARIMA模型的初步构建

ARIMA预测模型即自回归移动平均模型，该模型是一种重要的时间序列分析的方法[8]。其中，ARIMA(p,d,q)为差分自回归移动平均模型，AR是指自回归，MA指移动平均，p、d、q分别指的是自回归项、移动平均项数、差分次数，其一般公式表示为

(4)

式中：L为滞后算子(Lag operator)；d∈Z,d>0。

3 模型的识别与选择

3.1 模型的识别

差分处理完成后，已经得到一个平稳的时间序列，即使d=1。接下来，即要选择ARIMA模型中合适的p、q。而自相关函数和偏相关函数常常应用在ARIMA模型中的识别中。故本文根据自相关函数和偏相关函数来选择最合适的ARIMA模型，并得到自相关函数图(ACF)和偏相关函数图(PACF)。基于此，通过对图4和图5分析可知，自相关函数和偏相关函数两者均具有拖尾性，故最终选择ARIMA(20,1,3)和ARIMA(15,1,3)模型进行对比。

图4 自相关图1(ACF)

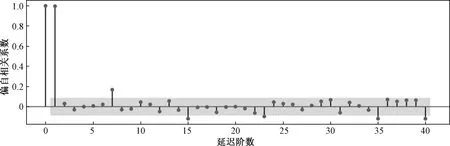
图5 偏自相关图1(PACF)

3.2 模型的选择

AIC信息准则是一种可以衡量统计模型拟合优良性的重要准则。一般情况下，要选取AIC值最小的概率分布函数，作为拟合原始观测数据[9]。通常情况下，AIC(p,q)定义为

AIC(p,q)=nln(σ2)+2(p+q)

(5)

式中，σ2为拟合ARMA(p,q)模型时残差的方差，它是(p,q)的函数，即AIC定阶的方法就是选择ARMA(p,q)最小的(p,q)作为相应的模型阶数。基于此，运用Python将各个模型的数值代入AIC准则进行计算，得到结果见表1。通过对比可知ARMA(20,1,3)模型所对应AIC值最小，故应该选择该模型用来预测光伏建筑一体化行业板块指数。

表1 各模型的AIC值

4 模型的检验

4.1 序列自相关和偏自相关检验

序列自相关和偏自相关常常用来检验ARIMA模型的残差序列。因此，根据该ARIMA(20,1,3)模型所产生的残差自相关图和偏自相关图(图6、图7)，可得序列残差基本为白噪声，即指在较宽的频率范围内，各等带宽的频带所含的噪声功率谱密度相等的噪声。

图6 自相关图2(ACF)

图7 偏自相关图2(PACF)

4.2 残差序列Ljung-Box检验

时间序列中一个最基本的模型就是高斯白噪声序列。对于ARIMA模型，其残差被假定为高斯白噪声序列，所以当用ARIMA模型去拟合数据时，拟合后要对残差的估计序列进行LB检验，判断其是否是高斯白噪声，而一般当Prob值小于0.05，就判断序列为非白噪声，但是经过上述运用Python进行LB检验，可以求得显著性水平Prob大于0.05(表2)，即相关系数与零没有显著差异，即该差异具有统计学意义。

表2 Ljung-Box 检验结果

续表2

4.3 正态分布检验法

正态分布检验方法是一种可以直观验证一组数据是否来自某个分布[10]，或者验证某两组数据是否来自同一族分布，通过Python编程所得散点图中的点随机散布在残差为0的直线上下，且趋势一致，证明该模型残差符合正态分布(图8)。

图8 残差正态分布检验图

4.4 误差分析

以沪深股市中 37 家光伏建筑一体化相关企业从2021年5月6日至5月28日的股票数据所求出的实际指数为实际值，并采用ARIMA(20,1,3)模型求解出该报告期间的预测指数为预测值，最终求解出相对误差的大小来进行误差分析。一般实际相对误差计算公式为

(6)

式中：δ为实际相对误差，由百分数表示；Δ为绝对误差；L为真值。

通过计算得到预测值与实际值对比如图9所示。

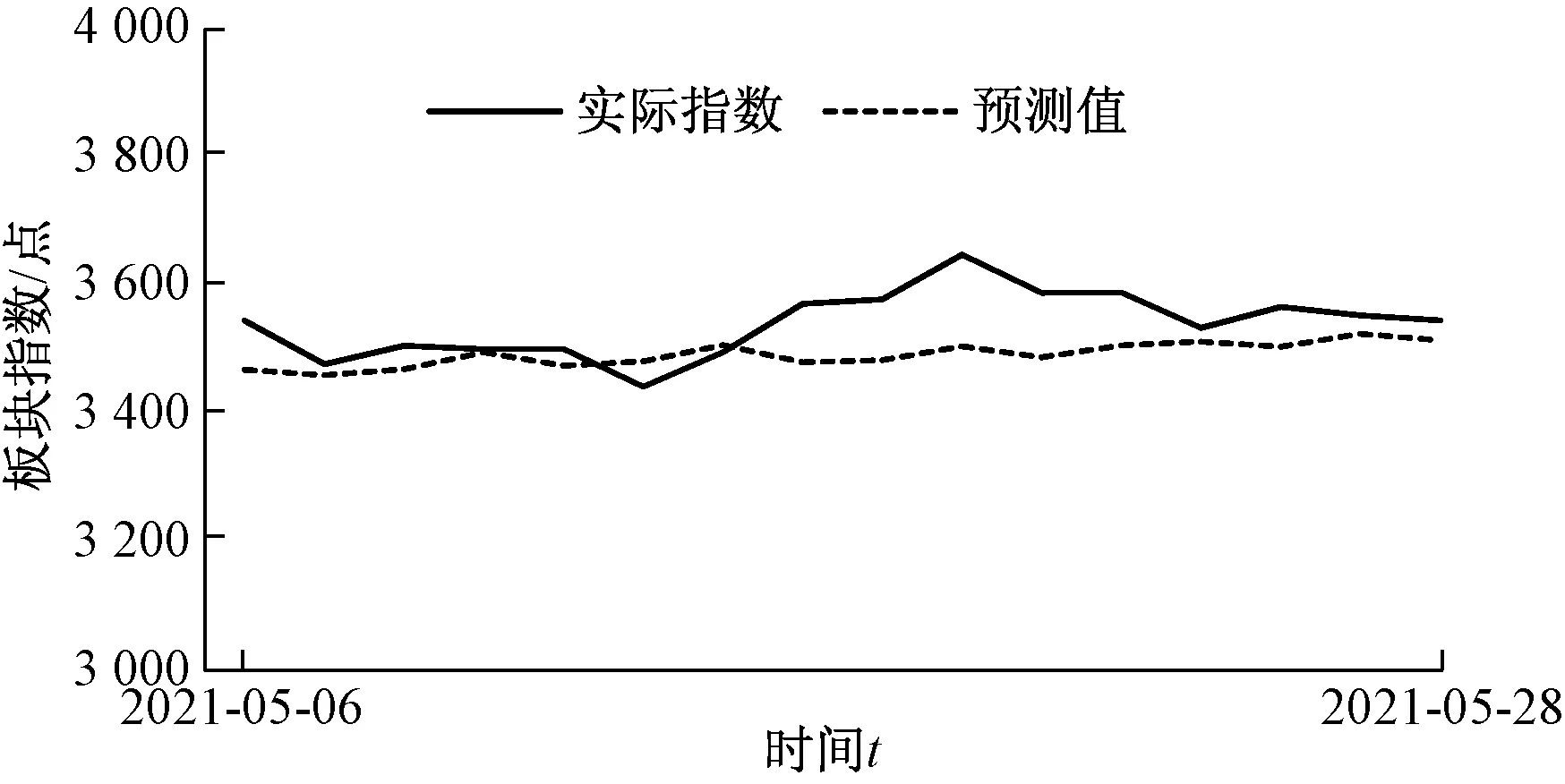
图9 实际指数与预测值对比(2021-05-06至 2021-05-28)

通过图10可知，ARIMA(20,1,3)模型预测出来2021年5月6日至5月28日指数数据的大小，与实际指数数据的实际相对误差的绝对值小于0.05，可以证明预测数据吻合度较高，因此该模型预测可信度高，对研究光伏建筑一体化指数的发展趋势有着比较大的借鉴意义。

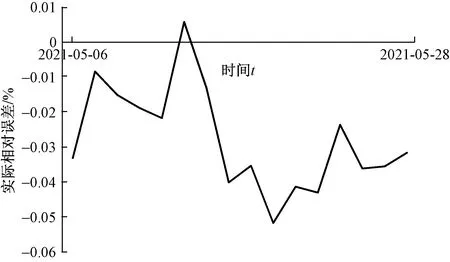
图10 实际相对误差(2021-05-06至 2021-05-28)

5 模型的预测

将2019年4月1日至2021年5月28日光伏建筑一体化板块指数数据代入ARIMA(20,1,3)模型中，预测出2021年5月31日至2021年7月30日的光伏建筑一体化板块指数图。根据图11分析结果可知，在未来两个月之内，光伏建筑一体化板块指数呈现“锯齿形”不断向上增长。而这预测结果也反映着该板块的投资利润和发展空间将继续上升，最终拉动该板块市值不断提高。而市场投资者和光伏建筑一体化行业企业管理者可以根据该预测图判断出适合的投资时间点，并合理地进行资金的投入与收回。

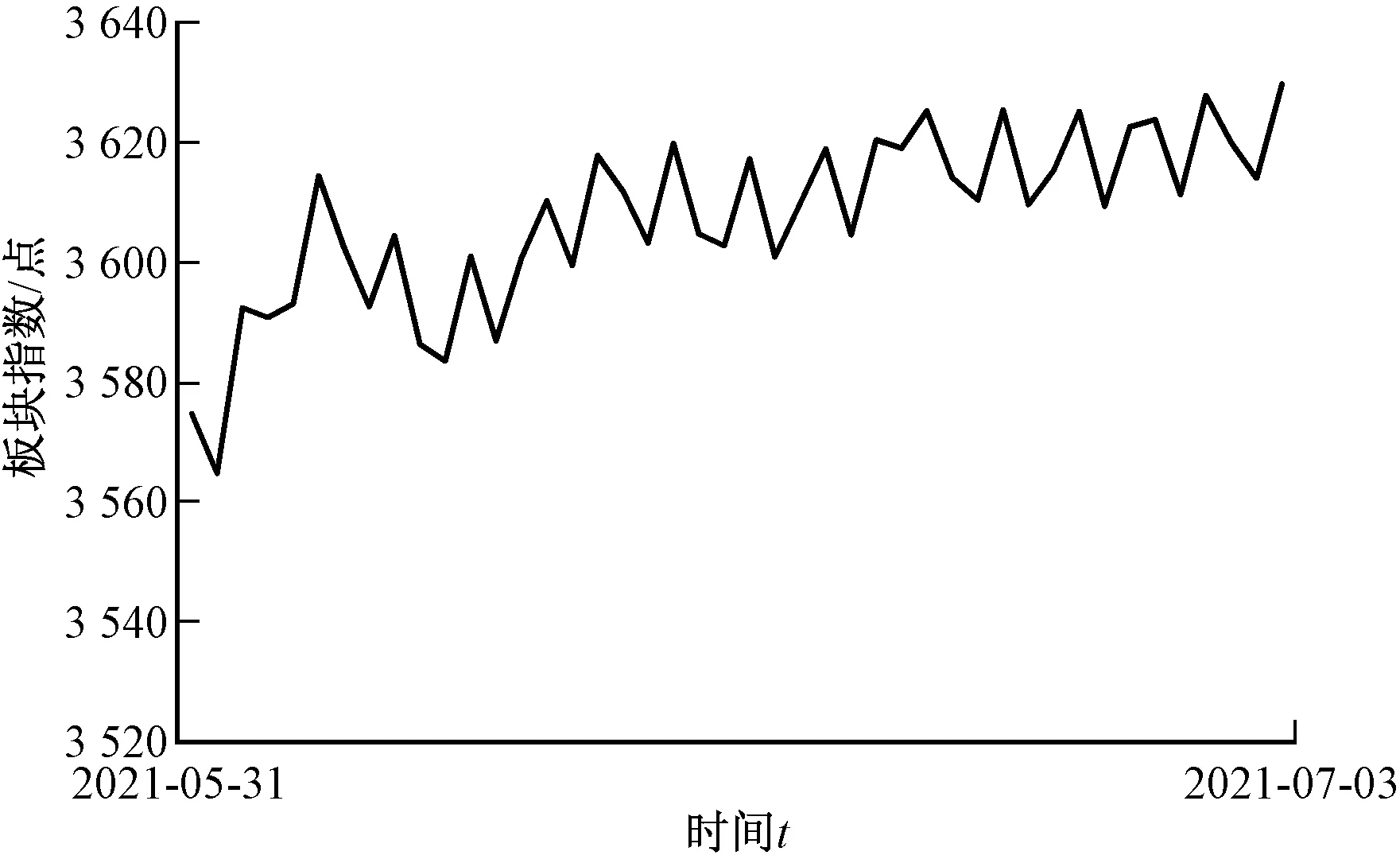
图11 光伏建筑一体化预测指数(2021-05-31至 2021-07-30)

6 结论与建议

通过建立ARIMA(20,1,3)模型对光伏建筑一体化指数发展进行预测研究，经过实例证明了该模型通过Ljung-Box检验和正态分布检验来验证了模型的合理性，最后利用该模型对2021年5月31日至2021年7月30日的光伏建筑一体化板块指数其进行预测。研究显示，该模型通过误差分析可知该模型预测数据的实际相对误差较小，在短期内预测的可信度较高，为市场投资者和企业管理者做决定提供一定的参考意义。

由实证结果分析可知，光伏建筑一体化该板块指数将会呈现总体上涨的趋势，而这样的结果也离不开产业链供需关系影响，即由于该行业本身具有学习曲线，成本会随着生产经验的积累按照特定规律下降。同时，作为一个新兴产业，光伏建筑一体化行业的发展受到了政府政策的大力支持。正如2020年3月10日，国家能源局正式发布的《关于2020年风电、光伏发电项目建设有关事项的通知》，根据其中《2020年光伏发电项目建设方案》可知，分布式光伏这一应用领域为光伏建筑一体化带来了新的发展机遇。基于此，针对市场投资者和企业管理者分布提出以下建议：

对于市场投资者而言，投资决策时不仅要考虑收益率，同时要考虑风险性，如中国对“碳达峰”“碳中和”高度重视，也相继出台光伏建筑一体化行业支持政策，但存在政策实施不达预期的可能性；或者光伏建筑一体化项目进展受较多因素影响，存在落地不达预期的可能性。因此，投资者可以采用多元化的投资策略，来分散投资风险。

对于从事光伏建筑一体化行业的企业而言，应该继续致力于提高光伏材料的转化效率，突破光伏建筑一体化发展中面临的主要技术瓶颈和供应链瓶颈，以此获得更加有利的市场竞争优势。同时，企业还应该顺应国家政策的意图，提升光伏建筑一体化产品应用场景的丰富度，在全面提升光伏建筑一体化产品性能的同时，实现高效发电功能与可靠建材功能的一体化完美结合，最终实现企业价值的增值。