基于区间贝叶斯网络的复杂系统可靠性分析*

熊娜，梅天宇，李飞

(1.南昌理工学院，江西 南昌 330044；2.湖北宜昌长江三峡游轮中心开发有限公司，湖北 宜昌 443000)

0 引言

随着复杂系统朝着模块化、集成化方向发展，传统故障树分析方法在复杂系统可靠性分析中的局限性逐渐凸显出来[1-4]：①在故障树模型中通常假设事件发生概率为精确值，对于大多数复杂系统而言，故障数据收集十分困难，尤其是新型高端设备寿命长、价格贵、可靠度高，难以通过试验方式获取足够的失效数据；②在故障树模型中假设各个事件只有正常运行与故障失效2种状态，忽略了介于二者之间的退化状态，根据划分标准的不同，可能是一个状态或多个状态。针对数控刀架卡死故障树模型中各事件发生概率难以确定的问题，刘英等[5]应用模糊数学建立了概率模糊数，进而确定顶事件发生的概率区间。邓耀初等[6]应用D-S证据理论表征故障树底事件发生概率的置信区间，依据区间算子确定了顶事件柱塞泵故障的概率范围。为了准确描述故障退化过程，刘晨曦等[7]在传统故障树模型中引入多状态事件和多状态表决门，经最小路集法确定了系统可靠度及底事件重要度。

故障树模型构建容易，但是，可靠性分析计算过程复杂、逻辑推理单向，难以根据新获取信息进行模型更新。贝叶斯网络具有表达事件多态性、模糊性和不确定性的优势，通过学习新样本可以调整有向无环图结构、修正条件概率值，并且可以根据新信息及时进行正向推理和反向推理[8-9]。鉴于现场数据缺乏、故障模式与失效机理多样、工作环境多变等原因，贝叶斯网络根节点故障率往往用具有一定模糊性的区间值表示，在某些特定情况下，区间值的上下限也无法用精确值进行描述。因此，本文将在故障树模型基础上构建基于区间贝叶斯网络的复杂系统可靠性分析模型。

1 贝叶斯网络建模过程

1.1 贝叶斯网络概述

贝叶斯网络[10-11]有向无环图结构由一系列节点和节点之间的有向边构成，有向无环图中的每一个节点代表一个随机变量，2个节点之间的有向边代表节点之间的条件概率关系。没有前续输入的节点为根节点，没有后续输出的节点称叶节点，既有前续输入又有后续输出的节点为中间节点。根节点具有表示该节点处于不同状态的先验概率，非根节点具有表征该节点与其父节点之间逻辑关系的条件概率，即该节点在给定父节点条件下处于不同状态的概率。以故障树结构为基础构建的贝叶斯网络模型不需要单独处理不交化过程以及确定最小割集，从而省去了不交化过程中的繁琐计算。贝叶斯网络模型通过调整条件概率取值表达节点间的不确定逻辑关系，正向推理表达节点间的关联故障，反向推理确定在给定系统故障信息条件下根节点处于各个状态的概率，以便及时发现系统中的薄弱环节。

1.2 贝叶斯网络双向推理

正向推理，也称预测推理，即根据贝叶斯网络模型中根节点处于各种状态的概率与条件概率关系确定叶节点处于各状态的概率。假设节点x1,x2,…,xn对应于故障树中的底事件、中间事件，则顶事件T处于状态Tq的概率表示为[12-13]

(1)

(2)

(3)

1.3 基于故障树结构的贝叶斯网络建模

典型的故障树逻辑门包括与门、或门、表决门等，由与门、或门构成的故障树结构与相应的贝叶斯网络模型如图1所示。故障树中底事件V1,V2,V3转换为贝叶斯网络中的根节点v1,v2,v3，中间事件M和顶事件T转换为贝叶斯网络中的中间节点m和叶节点t。假设0表示正常运行状态，1表示故障失效状态，那么故障树中与门、或门等布尔逻辑关系就可以通过条件概率值表现出来。在贝叶斯网络与门逻辑关系中只有当父节点v2和v3都发生时，子节点m发生。在贝叶斯网络或门逻辑关系中当

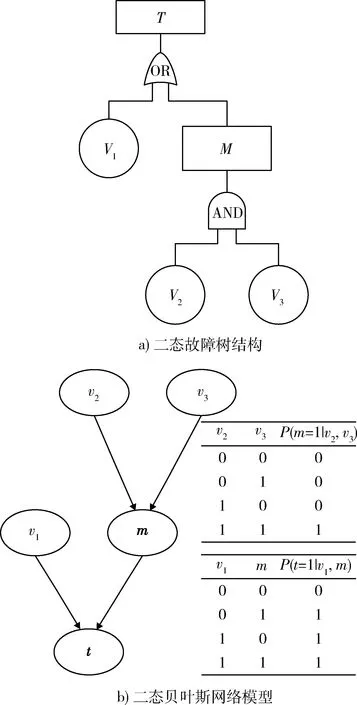
图1 逻辑与门、或门及对应的贝叶斯网络模型Fig.1 And gate,Or gate and corresponding BN model

父节点v1和m中有一个发生时，子节点t发生。多状态节点的贝叶斯网络结构与二状态结构相同，区别在于条件概率值确定，相关方法前期已开展过相关研究，不在此展开，具体可参考文献[4,14]。

2 基于区间模糊数的贝叶斯网络推理

2.1 三角模糊隶属函数

针对贝叶斯网络根节点(即故障树底事件)故障率难以用精确值描述的问题，引入具有一定模糊性的区间值表征。根节点从精确输入拓展到模糊输入，增强了贝叶斯网络可靠性分析的工程实用性，有利于表达已知信息不足或者主观判断引起的不确定性。对于有n个节点的模糊贝叶斯网络模型，假设第i个节点xi(i=1,2,…,n)有ki个模糊故障状态，表示为xi,j=(xi(1),xi(2),…,xi(ki))(j=1,2,…,ki)，用μij(0≤μij≤1)描述节点xi处于模糊故障状态j时的隶属度。对于一个给定节点，所有故障状态的隶属度之和为1，即

(4)

鉴于根节点失效概率往往在某一区间取值，越接近区间中值概率越大，因此，现有研究普遍采用运算简单、使用广泛的三角隶属函数描述各个节点的故障模糊可能性大小。假设贝叶斯网络节点xi在故障状态为xi(ki)时的模糊可能性表示为P(xi(ki))，相应的模糊子集表示为{gl,gm,gu}，其三角隶属函数表示如图2所示，其中，gm为模糊子集中心，gm-gl为模糊子集左模糊区，gu-gm为模糊子集右模糊区。

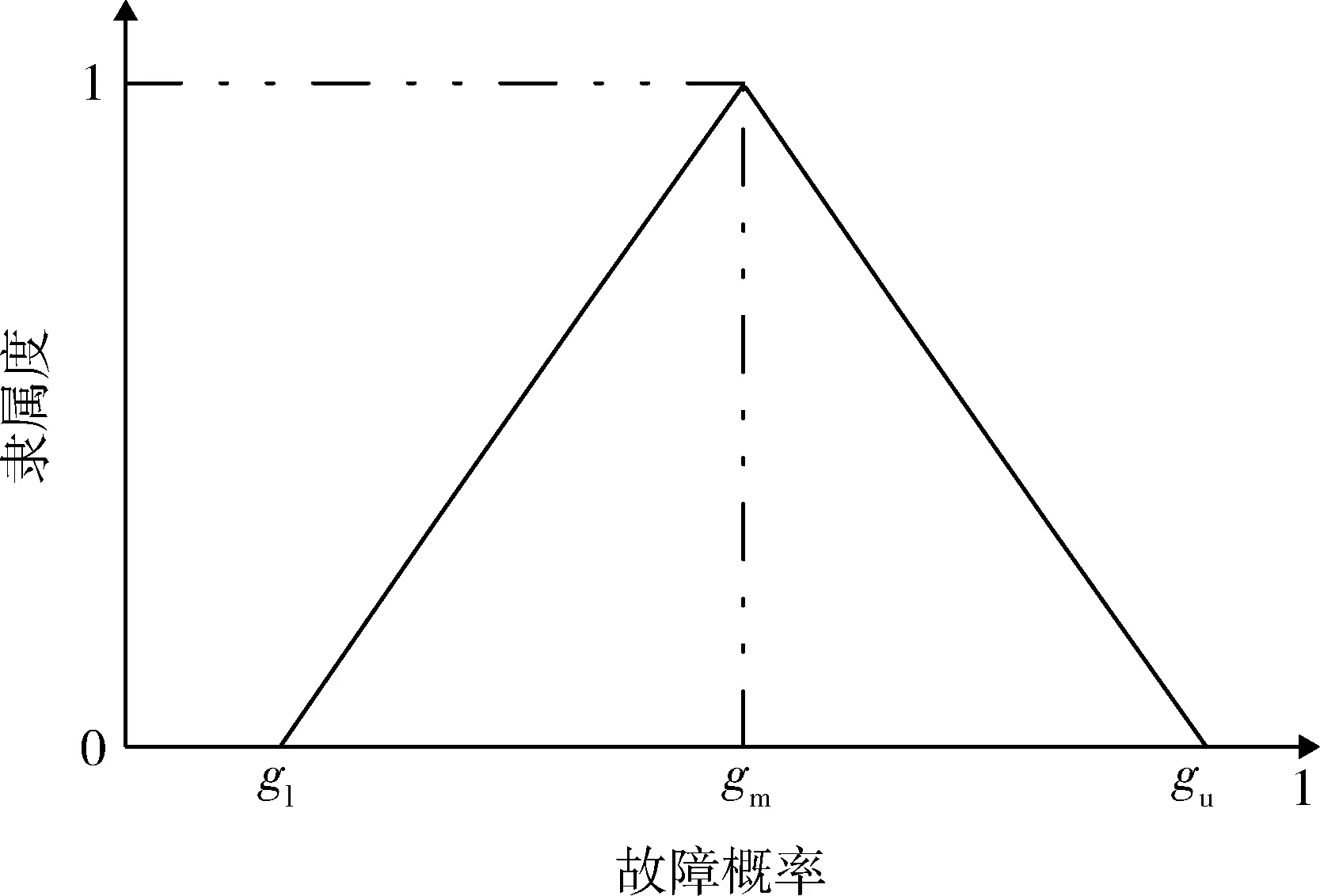
图2 P(xi(ki))的三角隶属函数Fig.2 Triangular membership function of P(xi(ki))

P(xi(ki))隶属函数表示为[15-16]

(5)

式中：g为故障概率。

2.2 区间三角模糊隶属函数

在工程实践中，有时候难以确定三角模糊隶属函数上下限，在此，引入区间变量表示三角模糊子集的上下限，则贝叶斯网络节点xi在故障状态为xi(ki)时的模糊可能性表示为

P′(xi(ki))=

(6)

如图3所示，P′(xi(ki))的隶属函数表示为

(7)

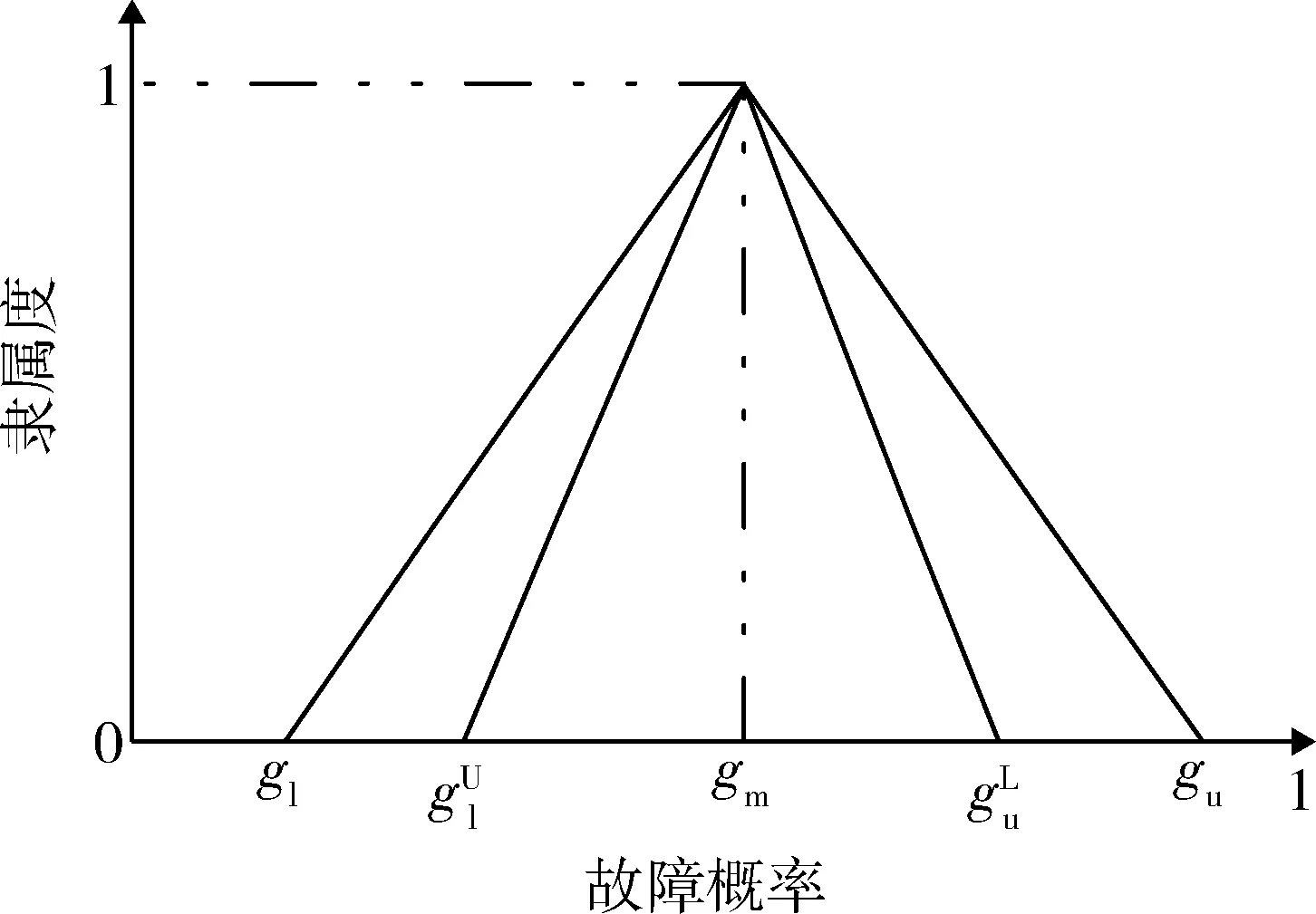
图3 P(xi(ki))的区间三角隶属函数Fig.3 Interval triangular membership function of P(xi(ki))

2.3 改进的贝叶斯网络推理

在贝叶斯网络模型中，假设n个根节点表示为xi(i=1,2,…,n)，m个中间节点表示为yj(j=1,2,…,m)，叶节点表示为T。在考虑贝叶斯网络根节点的模糊输入时，用xi(ki)(ki=1,2,…,li)表示根节点xi的故障状态，用yj(kj)(kj=1,2,…,lj)表示中间节点yj的故障状态，用Tv(v=1,2,…,l)表示叶节点T的故障状态。假设根节点各故障状态的区间模糊可能性表示为P′(xi,ki)，则叶节点T处于故障状态Tv的区间模糊可能性表示为

(8)

式中：π(T)为叶节点T的父节点集合；π(yj)为中间节点yj的父节点集合。

利用贝叶斯网络模型的反向推理机理，经去模糊即可确定根节点处于各个故障状态的后验概率。当叶节点T处于故障状态Tv时，根节点xi处于状态xi(ki)的后验概率表示为

(9)

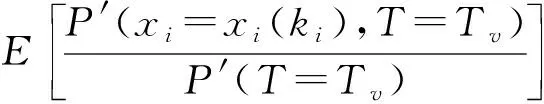
3 实例分析

3.1 控制系统故障树模型

以文献[14]中的导弹控制系统为研究对象建立故障树模型，如图4所示。控制系统故障由平台系统故障和姿态失去控制引起，前者由平台初始对准失效、导航计算机故障和加速度计故障引起，后者由模拟控制机故障和电动舵系统故障引起。平台初始对准失效由方位对准失效和水平对准失效引起。导航计算机故障由模拟控制机故障和无线电高度表故障引起。以部件的故障率为模糊子集的中心值，确定区间的端点值使得边界值与中心值在同一个数量级，各根节点故障状态为1时的模糊故障率、区间模糊故障率如表1所示。

图4 控制系统失效故障树模型Fig.4 FT model of control system in failure

表1 故障树底事件及故障率Table 1 Failure rate of bottom events in FT model of control system (10-3 h-1)

3.2 控制系统贝叶斯网络模型

根据1.3确定的故障树结构向贝叶斯网络转化原则，构建控制系统失效时的贝叶斯网络模型，如图5所示。

图5 控制系统失效贝叶斯网络模型Fig.5 BN model of control system in failure

X4与X5为三状态节点，即正常运行状态0、故障失效状态1外以及介于二者之间的中间状态0.5， 2个节点之间为逻辑或关系，其条件概率关系如表2所示。其余节点为二状态节点，X2与X6之间为逻辑与门，其余节点之间为逻辑或门。在故障树结构中重复出现的事件X2在贝叶斯网络中由一个节点表示。

表2 M3节点条件概率Table 2 Conditional probability of node M3

3.3 可靠性分析

当贝叶斯网络中根节点故障率为精确值时，如表1第3列所示，假设X4与X5故障程度为0.5的概率数据与故障程度为1时相同，则叶节点发生故障的概率为

应用文献[7]中计算多状态故障树失效率的方法可以得到相同的结果，这验证了贝叶斯网络建模的正确性。根节点与各中间节点的故障概率如表3所示。

(1) 根节点故障率为三角模糊子集

以表1中的三角模糊故障率为输入，根据式(1),(5),(8)推理确定中间节点失效的模糊可能性，如表3所示，进而确定根节点的模糊可能性：

以贝叶斯网络模型中精确故障率为故障率三角模糊子集的下限值、中心值、上限值，以根节点x1为例，其精确故障率对应的三角模糊子集为{16,16,16}(10-3/h)，经贝叶斯网络推理，确定叶节点处于故障失效状态的模糊概率子集上边界与下边界重合，验证了三角模糊贝叶斯网络模型的准确性与可行性。

(2) 根节点故障率为区间三角模糊子集

以表1中的区间三角模糊子集为输入，根据式式(1),(6)～(8)推理确定中间节点失效的模糊可能性，如表3所示，进而确定根节点的模糊可能性：

以贝叶斯网络模型中根节点故障率三角模糊子集的下限值为区间三角模糊子集下限变量区间的下边界与上边界，上限值为区间三角模糊子集上限变量区间的下边界与上边界，构建区间三角模糊变量。以根节点x1为例，三角模糊子集对应的区间三角模糊子集为{(6,6),16,(26,26)}(10-3/h)，经贝叶斯网络推理，区间三角模糊子集下限变量区间的下边界与上边界重合，上限变量区间的下边界与上边界重合，验证了区间三角模糊贝叶斯网络模型的准确性与可行性。

贝叶斯网络根据式(2),(3),(9)进行反向推理，经去模糊处理，确定各叶节点处于不同状态的后验概率，如图6所示。由于贝叶斯网络结构与条件概率关系没有发生改变，因此，在三角模糊输入和区间三角模糊输入条件下的后验概率值相同。当根节点故障状态为1时，叶节点X1处于故障状态的后验概率最大，为0.288 12；其次是根节点X4和X5，处于故障状态1的后验概率为0.185 22，处于故障状态0.5的后验概率为0.099 29。因此，当控制系统发生故障失效时，应该对后验诊断结果中失效概率较高的部件X1,X4和X5进行优先排查。

表3 非叶节点故障失效概率Table 3 Failure rates of leaf node and intermediate nodes h-1

图6 根节点失效时叶节点后验概率分布(10-3/h)Fig.6 Posterior probabilities of leaf nodes when the root node in failure (10-3/h)

4 结束语

本文将区间模糊子集引入贝叶斯网络中，提出了一种基于区间贝叶斯网络的复杂系统可靠性分析方法，直观明了地表征复杂系统可靠性指标的区间范围，经反向推理有效识别出系统可靠性设计中的薄弱环节，为故障诊断与改进设计提供意见建议。

(1) 结合故障树结构建模容易和贝叶斯网络双向推理的优势，构建了基于二者的可靠性分析模型，为多状态复杂系统可靠性分析提供了研究思路。

(2) 通过引入三角模糊函数、区间模糊子集，有效解决了根节点输入难以精确描述的问题，增强了基于贝叶斯网络的复杂系统可靠性分析方法的工程实用性。