基于GS-ARIMA模型的原油股票成交量预测研究

刘 敏 侯俊华

（东华理工大学 经济与管理学院，江西 南昌 330000）

一、引言

股票市场具有高回报、高风险的特性，驱使着人们对股票的波动性进行探究。[1]但是，很多因素如政治事件、社会活动等都会影响股票价格的变化，预测股票走势是一件极具挑战性的工作。[2]近些年机器学习方法在股票预测方面取得了不错的进展，相较于传统方法显示出了独特的优势。[3]于卓熙基于主成分分析与广义回归神经网络进行股票价格预测，预测结果良好。[4]邓烜堃利用DAE进行降维，其模型大大降低了运行时间。[5]刘恒等人将贝叶斯神经网络运用到股票时间序列预测中。[6]丹文基于GARCH模型对股票指数的拟合与预测取得了较好的预测效果。[7]通过上述研究表明，机器学习方法在预测方面具有明显的优势，在股票价格预测及降维方面已有不少研究。然而，目前很少对股票成交量波动进行预测的研究。针对原油股票成交量，建立基于网格搜索算法（GS）优化的差分整合移动平均自回归（GSARIMA），以期建立一种简单快速的股票成交量波动预测模型。

二、 ARIMA模型

ARIMA模型由Box与Jenkins于上世纪七十年代提出，是一种知名度很高的时间序列预测方法，也可简写为ARIMA(p,d,q)。

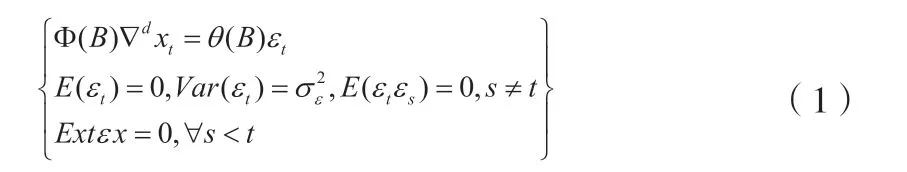
其中：

三、实例分析

采用2000年6月10号至2019年12月23号原油股票成交量的所有数据作为训练模型的数据集，共6000个样本数据。选取2000年6月10号至2019年3月18号的数据作为训练集，另外2019年3月18号至2019年12月23号的数据作为测试集，基于网格搜索算法建立GS-ARIMA模型，将模型预测值与实际值对比验证模型的准确性与可靠性。

应用ARIMA模型对数据进行分析与预测时，要求序列是由一个平稳随机过程产生，在图形上反映为所有的样本点都围绕着某一水平线上下随机波动，因此使用ARIMA模型之前需先判定数据的平稳性。对原油股票成交量的时间序列进行ADF检验，原始序列的检验结果如表1所示。

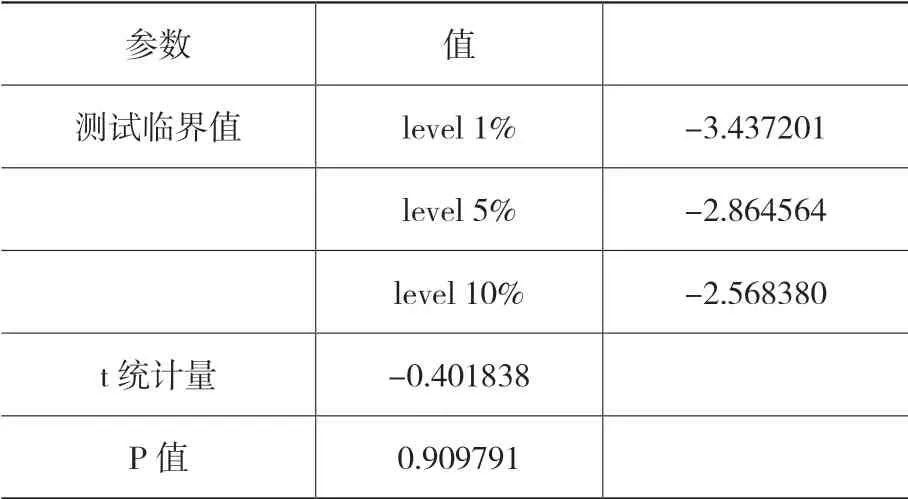
表1 原始数据ADF检验结果

通过表1中的ADF检验结果可得ADF值为-0.401838，明显大于3个level临界值，因此该时间序列显然是一个非平稳时间序列，必须采用差分处理才能进行下一步的建模工作。

（一）时间序列平稳性及非白噪声检验

对一阶差分后的时间序列开展平稳性检验，ADF检验结果如表2所示。经过一阶差分后，ADF值为-9.316945。其值小于3个level临界值，可证明差分后的序列是平稳的，并确定模型中d的值为1。同时白噪声检验结果的P值为1.01e-15＜0.05，拒绝原假设，确定该时间序列不属于白噪声序列。

表2 原始序列一阶差分ADF检验结果

（二）模型识别与定阶

基于AIC最小准则，得到最优值为AIC（6,5），并基于BIC准则和网格搜索算法进行超参数优化得出p～（0～7）、q～（0～7）下 的AR（p）、MA（q）热 力图，如图3所示。通过热力图展示和AIC（6,5）确定出模型参数p=6，q=5。以此确定GS-ARIMA（6,1,5）为原油股票成交量预测的最佳模型。

图1 基于BIC 准则的AR×MA热力图

（三）模型诊断

对原油股票成交量预测之前需要进行模型诊断，诊断结果如下图2所示，从标准化残差序列图（左上图）、残差直方图+概率密度图（右上图）、残差QQ图（左下图）、残差自相关图（右下图）进行讨论，判断其模型信息是否提取充分。

图2 模型诊断图

随着时间的推移（左上图）的残差没有显示任何明显的季节性，初步断定为是白噪声，并通过右下角的自相关（即相关图）证实，表明时间序列残差与其本身的滞后具有低相关性。在右上图可以看出， KDE线（残差概率密度线）分布与正态分布N(0,1)相似，均值近似为0，只是标准差有差异，这表明残差符合良好的正态分布。同时，左下角的QQ图显示，残差的有序分布几乎遵循采用N(0,1)的标准正态分布采样的线性趋势。

通过上述模型诊断分析，可采用GS-ARIMA（6,1,5）模型对原油股票成交量时间序列进行建模并预测。

（四）模型预测与评价

运用GS-ARIMA（6,1,5）对2019年3月18号至2019年12月23号原油股票成交量进行预测，其预测结果如图3所示。从图3可以看出，预测值和观测值的变化波动具有较好的一致性，说明GS-ARIMA（6,1,5）模型取得了良好的预测效果。

图3 ARIMA模型预测值与观测值对比图

取最后10个预测结果与观测值进行数据对比分析，分析结果如表3。从表3中分析结果可以看出，负值相对误差较多说明所选预测结果比观测值稍大。表中所列相对误差几乎都在2%～9%范围内波动，且GS-ARIMA（6,1,5）模型的决定系数R2值为0.920818，进一步表明GS-ARIMA（6,1,5）模型预测原油股票成交量具有较好的预测效果。

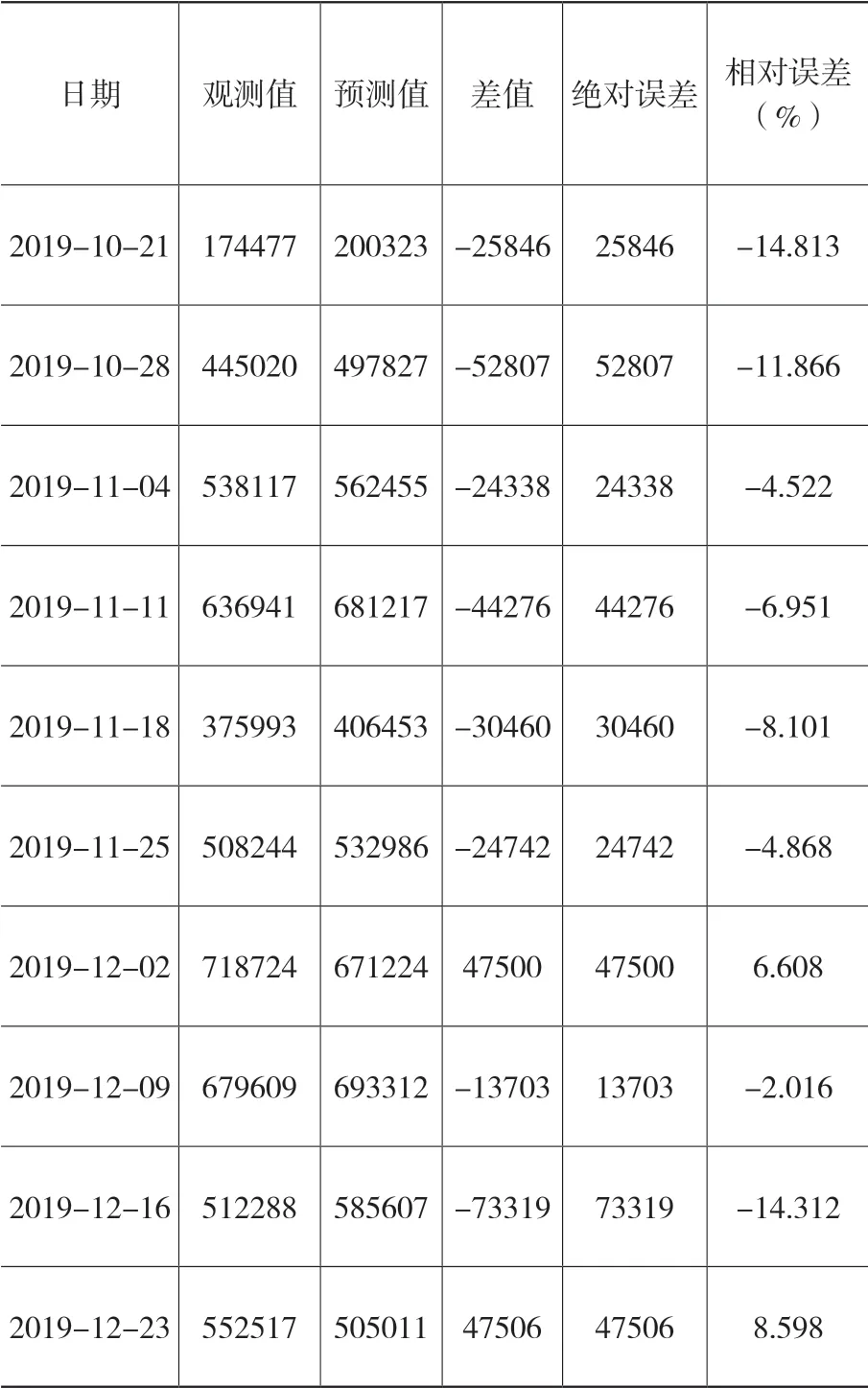
表3 预测值与观测值对比分析结果

四、结语

以2000至2019年原油股票成交量为例，首先分析原油股票成交量数据特征，通过差分方法得到剔除波动特性的平稳序列，并基于网格搜索算法拟合出最优模型GS-ARIMA（6,1,5）。利用该模型预测2019年3月18号至12月23号的原油股票成交量与真实观测数据比对，相对误差大概率在2%～9%范围内波动，且所训练的GS-ARIMA（6,1,5）模型的决定系数R2为0.920818，表明应用GS-ARIMA（6,1,5）模型预测未来原油股票成交量具有一定的参考价值。