50 kW 级高功率霍尔推力器放电通道数值模拟研究

陈笃华，王平阳，王 尚，刘 佳

（1.上海交通大学 机械与动力工程学院，上海 200240；2.上海空间推进研究所，上海 201112）

0 引言

高功率霍尔推力器具有高比冲、大推力、长寿命以及参数可调范围广等优势，通过调节工质流量和放电电压可满足空间任务在不同阶段对推力器的性能需求，并大幅度节约燃料。同时，高功率霍尔推力器工作时也有着因放电通道内产生较高密度等离子体导致的热负荷以及温度过高引起的磁路元件性能下降等问题。数值仿真可得到推力器详细参数分布，为推力和比冲的计算提供放电通道内部电势、等离子体数密度、电子温度等具体参数，同时也能通过计算结果分析放电通道内等离子体生成机理和推力器热负荷。上述工作为推力器性能分析及优化设计提供详细理论支撑，具有重要参考价值。

对于霍尔推力器的数值模拟研究由来已久，俄罗斯的MOROZOV 等采用一维流体动力学模型对霍尔推力器进行数值模拟分析，得到了一维条件下的粒子参数稳态解析解和时变动态解；麻省理工学院FIFE提出了二维高精度的单元粒子法（Particle-in-Cell，PIC）计算模型，用以计算从通道内到羽流场的霍尔推力器粒子运动过程及电子温度、电场强度、磁感应强度、粒子数密度分布等参数；加州理工学院MIKELLIDES 等采用二维轴对称条件下的磁场网格一致性等离子体求解程序对NASA-300 M 型霍尔推力器进行仿真，得到了标准工况下（放电电压300 V，放电电流40 A）推力器通道内及附近羽流场的电势分布、电子温度、电子数密度等参数；上海交通大学严立等模拟了SPT-70 加速通道的粒子参数分布以及粒子碰撞类型对流场分布的影响，并考虑了工作过程中生成的等离子体对加速通道壁面的相互作用所导致的热效应。相比于中低功率推力器研究进展，目前对于多工况下的高功率霍尔推力器性能仿真研究工作国内鲜有报道。

为配合50 kW 级高功率霍尔推力器的样机设计与实验研究工作，本文基于PIC/蒙特卡罗碰撞模型（Monte Carlo Collision，MCC）/直接模拟蒙特卡罗碰撞模型（Direct Simulation Monte Carlo，DSMC）方法针对特定结构的50 kW 级高功率霍尔推力器进行了二维数值模拟仿真研究，得到多种稳定运行工况下推力器通道内部的粒子参数分布；并依据仿真结果，分析推力器内部工作过程以及推力器的热损失功率情况，并计算了推力器推力及对应比冲。此项研究工作可为改进推力器构型、提高推力器工质效率和开展高功率霍尔推力器地面试验提供理论依据和技术参考。

1 数值仿真

1.1 计算基本模型

本文采用了PIC/MCC/DSMC 方法对推力器的工作过程进行了数值模拟工作：PIC 主要用于粒子运动过程跟踪求解和通道内自洽电场求解；MCC 主要用于求解相对速度较大的电子和中性粒子之间的碰撞过程；DSMC 主要用于求解相对速度较小的中性粒子和离子相互之间的碰撞过程。三者综合使用以完整模拟推力器工作时的等离子体流动。

基于PIC 计算时采用了静电求解模型，电场的微分解析通过泊松方程给出，即

式中：

Φ

为电势；

ρ

为电荷密度；

ε

为真空介电常数。

泊松方程的求解考虑五点差分形式，为了提高计算的收敛速度，采用超松弛迭代法。计算模型霍尔推力器的阴极中置于推力器中部，如按照真实位置对阴极及电子运动轨迹进行模拟，则需要极大的计算量并难以捕捉电子的真实运动轨迹，故此选择虚拟阴极。考虑以准中性入射模型建立虚拟阴极，在计算的每一时间步长内通过区域边界向等离子体入射一定量的电子以维持靠近阴极边界区域的准中性条件。具体的处理方式为计算阴极边界所有网格总的净离子数目，计算式为

如果Δ

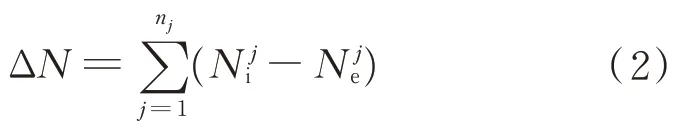
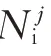
N

>0，则总的离子数目大于电子数目，偏离电中性，需要在边界打入相应的电子，以麦克斯韦分布方式打入；如果Δ

N

<0，则总电子数目大于总离子数目，不需要打入电子。

在推力器运行过程中原子速度为百米每秒量级，远远小于离子和电子的运动速度，可以认为计算模型中的原子为近似背景场。原子的分布情况满足通道等离子体扩散准则，考虑在模型中电子与原子碰撞只生成一价离子，电子与原子碰撞的概率为

式中：

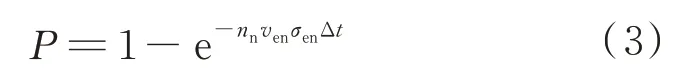
P

为碰撞概率；

n

为中性原子的数密度；

v

为电子和中性原子的相对速度，可近似为电子速度；

σ

为电子和中性原子碰撞截面的总和，包括弹性碰撞截面、激发碰撞截面和电离碰撞截面，与电子能量分布相关；Δ

t

为时间步长。

内部的碰撞过程主要为电子与原子、离子之间的碰撞，忽略中性粒子相互之间的弹性碰撞。对于3 种粒子（中性粒子、氙离子、离子电荷）相互间的碰撞情况，对于中性粒子而言，碰撞集中发生在缓冲区和电离区，数密度相对较大。对于离子而言，相比原子有着较高的速度和能量，加速喷出的离子即为推力器推力来源。粒子的运动和加速通过解耦计算获得，通过计算电场得到粒子所受电场力，通过磁场分布得到粒子所受磁场力，再进一步计算粒子的加速度和速度。

计算达到稳定后，以粒子为基本单元统计其在阳极表面和放电通道内外壁面的能量沉积所引起的推力器热损失情况。推力器加速通道内中性粒子能量较低，可视为与壁面处于热平衡状态；产生的电子质量较小，在鞘层电势影响下与壁面的碰撞过程受抑制，因此，能量沉积计算中忽略电子的热流作用，只考虑离子在加速通道陶瓷壁面的能量沉积。等离子体沉积到加速通道壁面上的能量为

式中：

q

为等离子体沉积在壁面的总能量；Δ

q

为碰撞过程中离子动能的变化量；Δ

q

为离子内能的变化量；

e

为电荷量；Δ

Φ

为鞘层电势。

整体计算流程可描述为：初始化计算模型，对计算域进行网格划分，将磁场数据耦合加载到计算程序，对各类物理参数初始化和粒子进行初始分布。根据工质流量在计算的每个时间步长入射对应数目中性氙原子，依据准中性入射模型入射对应数目电子，根据粒子的现有速度计算其运动状态。通过PIC 建立粒子间的电磁场作用模型，通过DSMC 计算原子、离子间的碰撞和动量交换、电荷交换，通过MCC 计算电子和原子间的碰撞。通过求解泊松方程得到电势、电场分布，再依据载入的磁场数据计算粒子的加速度与速度。通过所编写程序判定流场中的粒子净流量小于某初设值时，则视为计算进行至推力器完全稳定工作状态，输出计算结果，若不稳定则继续进行计算。计算至稳定状态后，统计相关参数。

1.2 计算区域及网格划分

模拟计算的50 kW 级霍尔推力器为轴对称型结构，该推力器在周向上各类参数分布均匀，因此采用二维对称计算模型可模拟推力器运行基本情况。数值计算时所选取的计算区域如图1 所示。主要包括推力器的放电通道、出口及部分羽流区域，其中左侧边界为推力器阳极，以推力器中心轴线为对称轴。根据推力器的固有尺寸，放电通道的长度

L

=95 mm，其中内壁面处于

R

=165 mm处，外壁面处于

R

=235 mm 处，在加速通道外部选取半径为400 mm、轴向长度95 mm 的圆柱形羽流场区域。采用结构化均匀网格，网格单元长度选取为2.5 mm。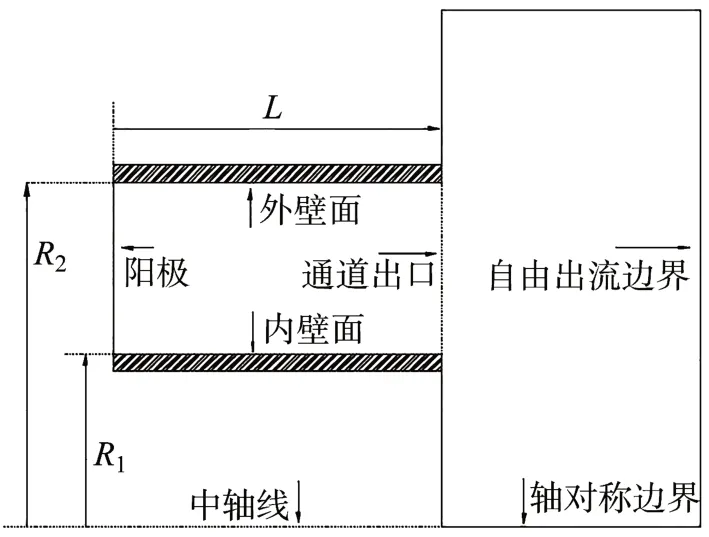

图1 推力器结构及流场仿真区域Fig.1 Construction and simulation zone of the thruster

1.3 加速计算说明

工质氙原子和电子的质量相差5 个数量级，在相同的能量条件下，氙原子通过加速通道的时间约为电子的500 倍，若按照电子的时间步长推进离子，将花费大量时间和计算资源达到稳定，故此计算中采用降低氙原子质量和提高介电常数的办法以提高计算速度。具体表现为将氙原子质量降低2 500 倍，则运动速度相应提高50 倍；将介电常数提高100 倍，德拜长度提高10 倍，总体上降低时间步长，提高空间步长。

1.4 推力及比冲计算

推力器工作时放电通道内生成的离子在电场作用下加速喷出产生推力，在单位时间内推力器获得推力等于从通道内喷出离子的总动量。对推力器标准工况进行数值模拟，统计推力器稳定工作时通道出口的离子数目及轴向速度。根据已知的氙离子质量（Xe），可得单位时间内的离子总动量，进而计算推力。再根据比冲定义，即可计算比冲为

式中：

I

为比冲；

F

为推力；

m

为单位时间内的工质流量；

g

为重力加速度。

2 标准工况数值模拟

2.1 磁场分布

推力器磁场考虑为静态磁场，由ANSYSMAXWELL 商用软件计算得到分布结果，以输入文件形式将磁场数据加载至模型计算程序。计算所得放电通道中轴线上磁感应强度分布如图2 所示，从阳极出口到羽流近场，整体呈先上升再下降趋势，最大值220.12×10T 出现在通道出口附近，符合霍尔推力器内部磁场设计准则及分布规律。

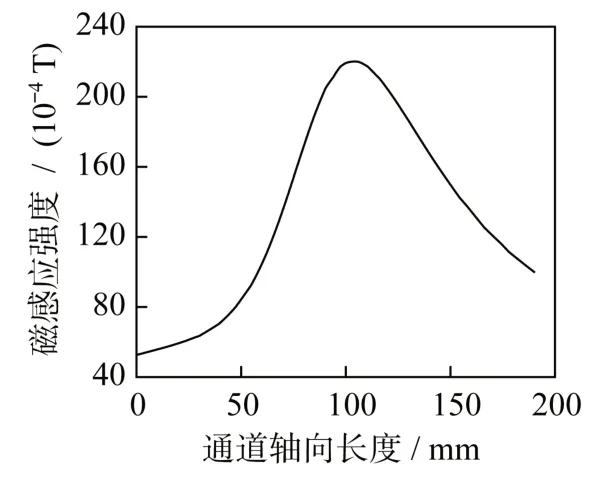
图2 通道轴线磁感应强度分布Fig.2 Distribution of the magnetic flux density along the channel axis

2.2 标准工况内部参数分布及性能参数

对标准工况下的50 kW 级推力器工作情况仿真分析，得到了放电通道内的粒子数密度分布、电子温度、离子通道轴向速度等结果。标准工况的输入参数包括功率50 kW，放电电压500 V，工质流量为86.4 mg/s。离子数密度分布如图3 所示，最大值出现在通道中间区域，最大值为1.635×10m，随着通道内电磁场对氙离子加速，数密度迅速降低，在通道出口位置的氙离子数密度约为1.679×10m。沿通道轴向离子数密度先增加后降低，分布情况和HOFER 等的结果相似，推力器放电通道内分为明显的缓冲区、电离区和加速区，满足放电通道粒子分布特征。通道内的速度分布如图4所示，离子速度在通道后半段迅速增加，并在电场作用下保持加速效果至通道出口，最大出口速度达到了28 150 m/s。

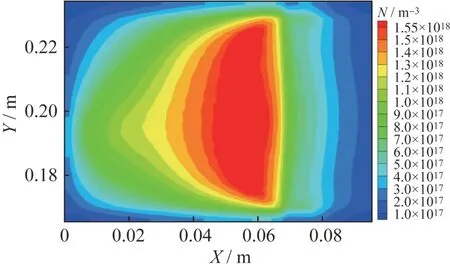
图3 标准工况下离子数密度分布Fig.3 Distribution of the ion number density under the standard condition

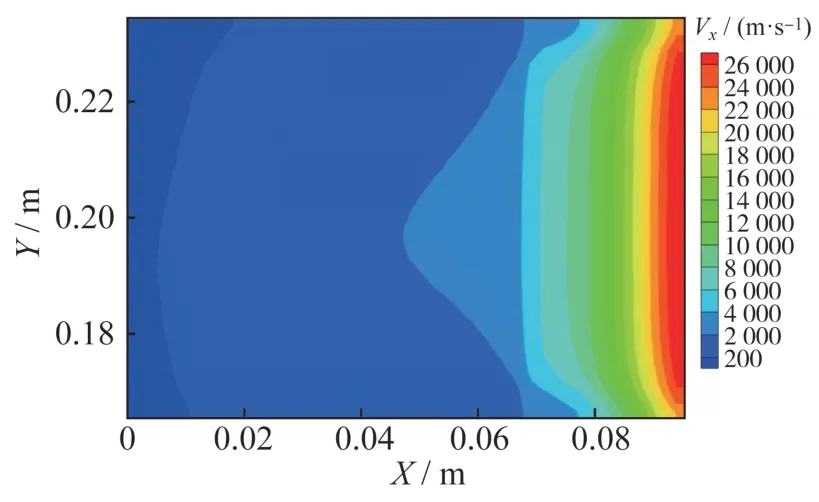
图4 标准工况下离子轴向速度分布Fig.4 Distribution of the ion axial velocity under the standard condition

统计可知，在考虑壁面典型平均温度600 K 条件下，标准工况下的推力器放电通道内壁面的热损失功率为3 068.97 W，外壁面的热损失功率为4 191.84 W，阳极表面（温度750 K）的热损失功率为710.91 W，推力器整体热损失功率占总功率比重为15.94%，与文献［10］的计算结果相比偏小，推力器在稳定运行时存在一定的热负荷问题。

利用标准工况计算得到的流场参数，结合1.4 节的方法和式（4）分别获得了推力为2.2 N，比冲为2 598 s，与文献［16］中同类50 kW 级霍尔推力器实验结果比较，推力和比冲的误差分别为5.18%和3.35%。

3 多工况模拟

推力器实际运行过程中根据空间任务需要，需在多种工作模式下稳定运行。控制推力器输出的主要方式包括调节工作电压和工质流量，针对上述工作情况，本章选择了标准工况工质流量、不同放电电压和标准工况放电电压、不同工质流量的输入条件，对多种工况下运行的推力器进行仿真研究。

3.1 不同放电电压

文中计算模型推力器在设计最佳运行条件下的放电电压为500 V，考虑实际需求偏离标准放电电压正负20%，选取放电通道中轴线上的计算结果输出。

电子温度随放电电压的变化如图5 所示，在不同的放电工作电压下，电子温度呈现相同的变化趋势，分布趋势与文献［17］中结果一致，电子在磁场中绕磁力线作拉莫尔回旋运动，磁场强度决定了放电通道约束电子能力的强弱。电子温度从阳极到通道口的轴向分布趋势和磁场分布趋势近乎相同，可以说明磁场对电子有明显束缚作用。不同差异点在于放电电压不同导致的电子温度最大值不同，偏差幅度与工作电压的变化幅度相近。

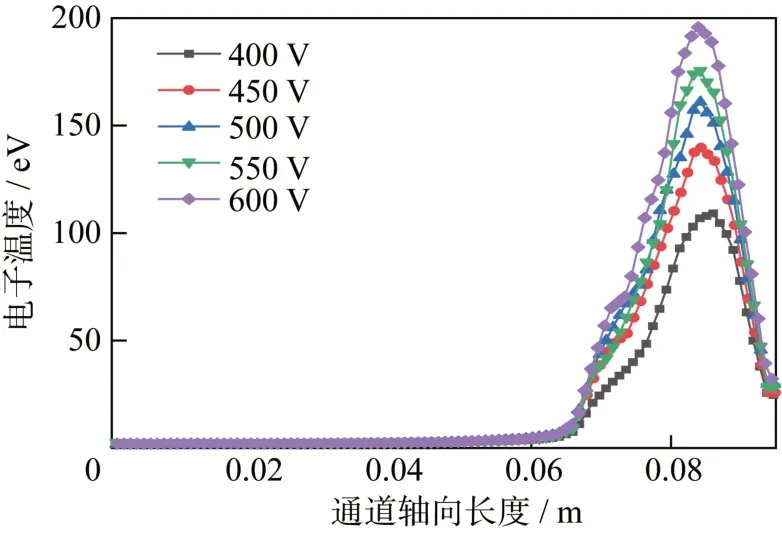
图5 不同放电电压下电子温度分布Fig.5 Distribution of the electron temperature at different discharge voltages

离子数密度的变化如图6 所示，不同电压下的数密度分布与标准工况下分布趋势基本一致，数值上放电电压越高，电子和离子的运动运动速度越大，碰撞和电离过程更剧烈，在通道中部的最大离子数密度越高。离子运动速度变化如图7 所示，工作电压的升高使离子在加速阶段获得更大的能量，电压越高，出口处离子运动速度越高。

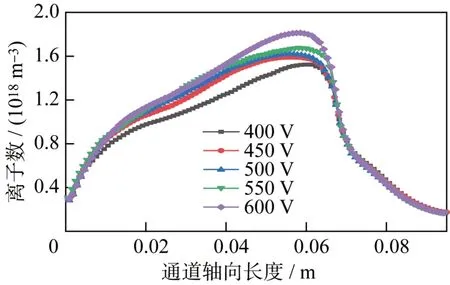
图6 不同放电电压下离子数密度分布Fig.6 Distribution of ion number density at different discharge voltages

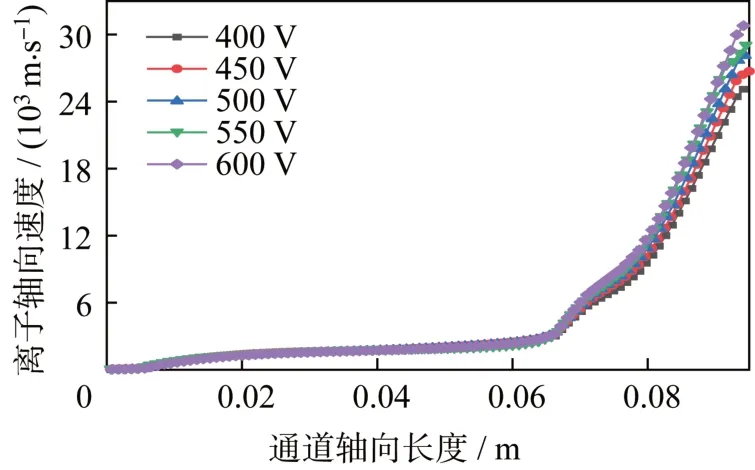
图7 不同放电电压下离子轴向速度分布Fig.7 Distribution of the ion axial velocity at different discharge voltages

3.2 不同质量流量

推力器设计标准工况下质量流量为86.4 mg/s，考虑实际需求条件偏离标准流量正负20%，统计结果显示，在69.12 mg/s 到103.68 mg/s 的输入流量下，推力器保持近乎相同的流场参数分布趋势。电子温度和离子数密度随质量流量的变化如图8～图9 所示，变化趋势相同，数值变化范围超过了流量变化的20%。在低流量时粒子数密度降低，粒子相互间的碰撞作用减弱，电子温度和生成离子的数密度进一步降低；质量流量越高，中间粒子的相互作用过程越剧烈，电子温度和离子数密度越高。离子运动速度在不同质量流量条件下分布近乎相同，如图10 所示，说明在此范围内的输入流量变化几乎不会影响通道内的粒子加速过程。

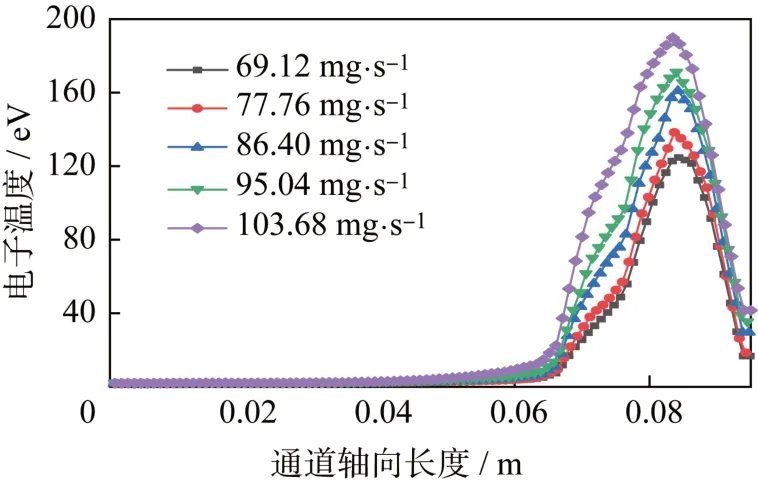
图8 不同质量流量下电子温度分布Fig.8 Distribution of the electron temperature at different mass flow rates

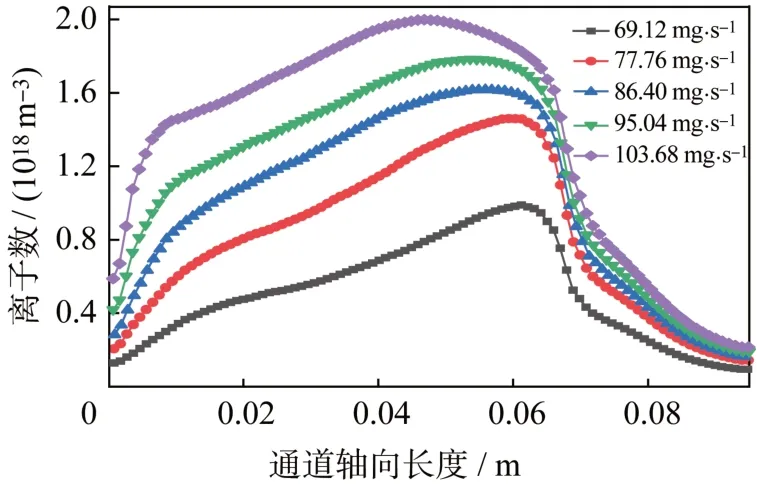
图9 不同质量流量下离子数密度分布Fig.9 Distribution of the ion number density at different mass flow rates

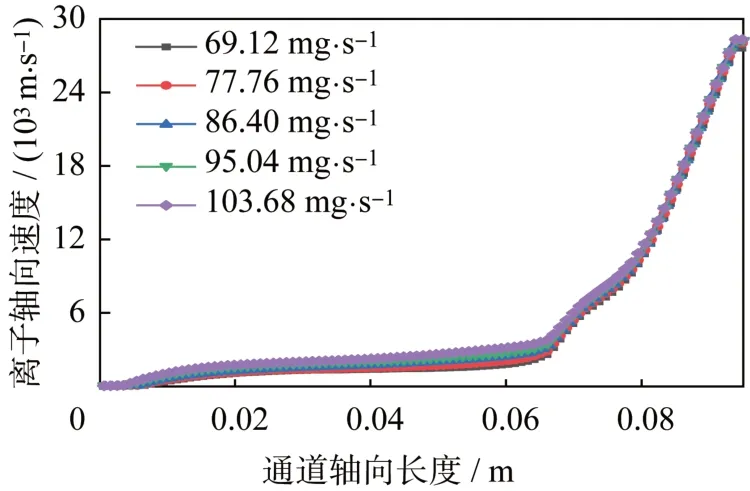
图10 不同质量流量下离子轴向速度分布Fig.10 Distribution of axis ion velocity at different mass flow rates

3.3 推力及比冲

推力器工作时推力和比冲直接体现了推力器工作性能，通过前面对放电通道内部过程的数值模拟，可得到出口所有粒子的速度和质量流量，进而求解推力和比冲。多工况下的推力和比冲如图11～12所示。

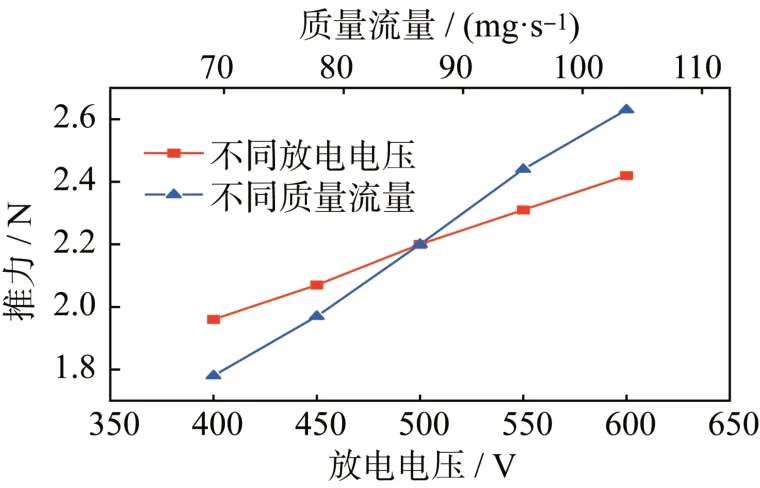
图11 多工况下推力Fig.11 Thrust under multiple conditions

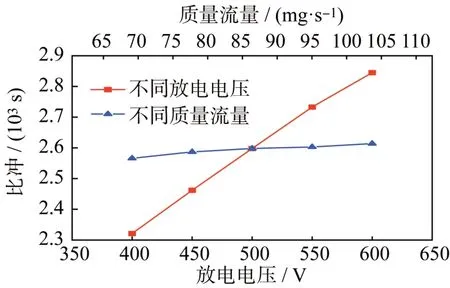
图12 多工况下比冲Fig.12 Specific impulse under multiple conditions

在相同流量下随着电压升高，出口离子速度越大，推力器比冲和推力越大；在相同工作电压下考虑工质流量变化，出口离子速度基本相同，比冲几乎不变，推力随流量增大而增大。

4 结束语

基于PIC/MCC/DSMC 混合数值模拟方法，计算了标准工况和其他工况下放电通道内部的等离子体参数，为后续50 kW 级高功率霍尔推力器的样机设计与地面试验提供了理论支撑，计算结果表明：

1）标准工况下，仿真结果与文献［16］中同类推力器实验结果比较，推力和比冲误差分别为5.18%和3.35%；通道内的离子数密度最大达到1.635×10m，随着通道内自洽电场对离子的加速作用，数密度在出口位置下降至1.679×10m，通道内分为明显的缓冲区、电离区和加速区。

2）标准工况下，阳极表面平均温度为750 K 和放电通道内外壁面在典型平均温度600 K 条件下的热损失占总功率的15.94 %，推力器存在一定的热负荷问题。

3）在工作电压400～600 V、质量流量69.12～103.68 mg/s 范围内考察了流场的分布情况。结果显示：工作电压提升会增加电子温度和离子出口速度；调节质量流量，电子温度和离子数密度分布趋势相同，离子速度基本不变。在此类工况条件下增大工作电压，推力比冲均随之增大；增大质量流量，推力随之增大，比冲几乎不变。