主余震型地震动过程的降维模拟

姜云木，阮鑫鑫，刘章军

(武汉工程大学 土木工程与建筑学院，武汉 430074)

地震灾害具有很强的破坏性与随机性，同时在一次主震后往往会伴随着多次余震的发生，且余震对结构造成的二次破坏不容忽视。由于主余震序列地震动记录数量有限以及对具体场地条件的限制，无法满足对结构计算的需求，因此，主余震型地震动的人工模拟备受关注。

建立合理的主余震地震动参数之间的关系，是精细模拟主余震型地震动的前提。相对于主余震复杂的震源机制等因素，工程师更关注主余震地震动的幅值、持时与频谱等工程特性的关联。在早期的研究中，学者们主要对主余震之间的峰值加速度、持时等参数关系进行了初步探索[1-3]。近年来，Zhang等[4]利用线性合成法拟合了主余震间震级、持时、能量等参数的关系。随后，Muderrisoglu等[5]估计了主震后一段时间内发生超越特定震级阈值的余震概率。此外，朱瑞广等[6]通过Copula函数较为完整地分析了主余震强度参数的相关性。Ruiz-Garcia等[7]研究发现：主震的场地卓越圆频率比余震的场地卓越圆频率有偏小的趋势，且具有中等的相关性。上述研究表明，主余震参数之间存在一定的相关性，但从工程实用角度来看仍需进一步的研究。

主余震型地震动的构造方法可分为确定方法和随机方法两大类。在确定方法方面：Hatzigeorgiou等提出了重复法来构造主余震序列，该方法假设主余震的特性一致，这显然不符合实际情况；Li等[8]提出了随机组合法构造主余震序列，即从主余震记录库中分别随机挑选出一条地震动记录组合成主余震序列，但该方法本质上得到的主余震序列不具有随机性。在随机方法方面：Hu等[9]首先利用调幅过滤白噪声方法生成主震，再利用分支序列法生成余震，但是该方法并没有考虑主余震间的条件关系与衰减关系；Nithin等[10]基于Priestley理论，提出了一种基于主震的余震条件缩放模型，并结合特定的场景生成了主余震时程样本。然而，该方法在本质上属于蒙特卡洛方法，为了保持模拟精度，需要成千上万的随机变量，导致了模拟时生成的样本数量庞大以及概率信息不完备的问题。综上所述，亟需建立一种能考虑主震与余震相互关联且高效实用的模拟方法。

基于上述研究进展，笔者首先在非平稳地震动过程的演变功率谱密度模型的基础上，对实测主余震记录的峰值加速度、场地土的卓越圆频率、阻尼比以及调制函数参数进行识别。然后，通过拟合优度检验，给出最优边缘分布和最优Copula模型。在此基础上，得到了主震参数条件下对应余震参数的条件均值。最后，结合谱表示-随机函数方法[11]，建立了主余震型地震动的降维模型，实现了主余震型地震动的高效模拟。此外，本文建立了主余震参数之间的实用计算公式，方便了工程应用。

1 时-频全非平稳模型参数的识别

1.1 非平稳地震动过程的演变功率谱密度模型

相对于震级和震源机制的地震学因素和“震源-传播途径-局部场地”的物理模型，地震工程更加关注地震动本身的幅值、持时与频谱等工程特性。因此，本文选用工程中经典的演变功率谱密度模型，该模型从地震动的频谱特性出发，能够反映地震动过程的非平稳性和统计特性。同时，通过建立主余震演变功率谱参数之间关系，可以方便地体现地震动的序列性。

根据非平稳随机过程的Priestley演变谱理论，非平稳地震动加速度过程的演变功率谱密度函数可表示为[12]

(1)

式中:SUg(t,ω)为非平稳地震动加速度过程Ug(t)的单边演变功率谱密度函数；A(t,ω)为时-频调制函数；S(ω)为平稳地震动加速度过程的单边功率谱密度函数。

对于时-频调制函数，采用Deodatis等[13]提出，刘章军等[14]改进的模型

其中,

(3)

式中:参数b=a+0.001;c=0.005；a为控制地震动过程衰减快慢的参数，s-1。一般地，a越大，地震动过程衰减越快。

对于平稳地震动加速度过程的单边功率谱，采用Clough-Penzien模型[15]

(4)

式中:ωg和ξg分别为场地土的卓越圆频率和阻尼比；ωf和ξf分别为基岩的卓越圆频率和阻尼比。一般地，可取ωf=0.1ωg，ξf=ξg。

在式(4)中，谱强度因子S0可表示为

(5)

式中:Amax为地震动峰值加速度的均值；r为峰值因子，在进行参数识别时取r=3。

1.2 演变功率谱密度模型的参数识别

由1.1节提出的时-频全非平稳模型可知，演变功率谱密度模型的参数向量可以表示为λ，即λ=[ωg,ξg,a]。需要指出的是，在进行场地土的卓越圆频率和阻尼比识别时，对实测强震加速度记录进行了调幅，因此参数向量λ中不包含地震动峰值加速度均值Amax和峰值因子r。于是，可定义演变功率谱密度模型的频域能量分布函数E(ω;λ)如下[16]

(6)

将式(1)和式(2)代入式(6)，积分可得本文模型对应的频域能量分布函数

E(ω;λ)=

(7)

记第i条实测记录的演变功率谱为Sug,i(t,ω)，如果放松演变功率谱的能量随时间分布再取其平均，那么对于第i条实测记录，可以得到其等价平稳过程的功率谱的函数Si(ω)如下[17]

(8)

由式(8)可得，第i条实测记录的频域能量分布函数Ei(ω)为

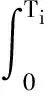
(9)

式中：Ti为第i条地震动记录的总持续时间；T0,i为第i条地震动记录的强震持时，具体可表示为[18]

(10)

(11)

(12)

式中:ai(t)为第i条实测地震记录时程；ωu,i为第i条实测地震记录时程的上限频率。

当取得一条地震动实测记录时，可以通过信号处理的方法得到实测记录的平稳功率谱Si(ω)，再根据式(9)与式(10)即可得到第i条实测记录的频域能量分布函数Ei(ω)。

根据主余震实测记录得到的频域能量分布函数曲线，采用最佳平方逼近准则，针对每条曲线分别识别参数向量λ

(13)

本识别方法原理简单，利用简单的频域能量相等原理，避免了在时频域上参数识别的困难，减少了计算量。且编程简单，仅需要3个主要的MATLAB工具箱函数便可以实现。

1.3 实测地震动记录的识别结果

本文在太平洋地震动工程研究中心的NGA-West2地震动数据库中严格按照以下原则[19]筛选地震波：

(1)主震记录与其对应的余震记录必须来自同一台站。

(2)余震只选取与主震对应且震级最大的余震作为研究对象。

(3)断层距离应大于10 km，以减少近断层效应的影响。

(4)主余震的震级应该均大于5，排除对结构影响不大的地震动。

经过严格筛选得到了17次地震的468组地震动记录。表1给出了本文所采用17次地震的地震名称、台站数量、震级、断层距范围和VS,30范围等基本信息。

表1 本文选取地震动记录的详细信息

本文根据GB 18306—2015《中国地震动参数区划图》[20]中建议的5种场地类别对实测强震记录进行筛选。为了将国外的实测记录与国内的场地类别相结合，众多学者研究建立了《中国地震动参数区划图》中场地类别与剪切波速VS,30的对应关系[21]。在本文中，采用文献[22]的场地划分标准。表2给出了不同场地类别对应的剪切波速VS,30范围与筛选得到的实测强震记录的数量。

表2 场地类别与VS,30的对应关系

对468组主余震加速度记录进行基线校正，并将峰值加速度调幅到200 cm/s2，利用1.2节的识别方法按照场地类别依次对演变功率谱密度模型的参数向量λ进行识别。

以CHY057台站分别观测的Chi-Chi地震主震和余震为典型实例。图1(a)和图2(a)分别给出了典型实例的主余震的实际能量曲线与模型能量曲线的对比，由图1(a)和图2(a)可知，模型能量分布曲线与实测记录的能量分布曲线拟合效果较好。同时，图1(b)、图1(c)、图2(b)、图2(c)给出了本文选取所有的II类场地主余震实测能量曲线与模型能量曲线的均值和标准差对比。可以看出，主余震模型能量曲线的均值及标准差与实测记录对比效果良好，充分说明了本文参数识别方法的有效性。

图2 余震能量拟合曲线

2 主余震参数的最优边缘概率分布

在本文中，除了对主余震记录的场地参数，即参数向量λ进行识别外，还提取主余震地震动实测记录的峰值加速度PGA。这样，考虑主震和余震，一共需要估计8个地震动参数的边缘概率密度分布。需要指出的是，提取主余震的峰值加速度未考虑场地类别，且均来自468组地震动记录调幅之前的统计结果。

图3 主余震地震动参数概率密度函数

在主余震参数的边缘分布参数识别完成后，需要采用AIC信息准则(akaike information criterion)判断最优的边缘分布模型。AIC值的定义如下[24]

AIC=2k-2lnL

(14)

式中:k为分布模型中参数的个数;L为模型最大似然函数。一般地，AIC值越小，代表模型拟合度越好。

通过AIC信息准则判断，并可得到主余震参数的最优边缘分布以及模型参数,如表3所示。当概率模型为对数正态分布时，Par1为均值，Par2为标准差；为Gumbel分布时，Par1为位置参数，Par2为形状参数；为广义极值分布时，Par1为形状参数，Par2为尺度参数，Par3为位置参数；为Weibull分布时，Par1为比例参数，Par2为形状参数。

表3 主余震时域参数与场地参数概率模型

3 基于Copula理论的主余震参数相关性分析

3.1 基本理论

Copula函数可以看作是一类联结联合分布函数和边缘分布函数的“纽带”，它描述了多维随机变量之间的相关性。根据Sklar定理[25]，二维随机变量(X1,X2)的联合分布函数F(x1,x2)及其边缘分布可写成如下形式

F(x1,x2)=C(F1(x1),F2(x2))=C(u1,u2)

(15)

式中:FXi(xi)(i=1,2)为随机变量Xi的边缘概率分布函数;C(·)为Copula分布函数。于是，二维随机变量(X1,X2)的联合概率密度函数可以表达为

f(x1,x2)=c(u1,u2)fX1(x1)fX2(x2)

(16)

式中：fXi(xi)(i=1,2)为随机变量Xi的边缘概率密度函数；c(·)为Copula密度函数，即

(17)

若将主震的某一参数(例如，场地土的卓越圆频率)视为随机变量X1，与其对应的余震参数视为随机变量X2，则在给定主震参数的条件下对应余震参数的概率密度函数可表达为

鼓粒成熟期是大豆积累干物质最多的时期，也是产量形成的重要时期。促进养分向子粒中转移，促粒饱增粒重，适期早熟则是这个时期管理的中心。这个时期缺水会使秕荚、秕粒增多，百粒重下降。秋季遇旱无雨，应及时浇水，以水攻粒对提高产量和品质有明显影响。大豆黄熟末期为适收期。当种子含水量达到13%时可以入库。

(18)

进一步地，条件均值可以表达为

(19)

从式(19)可知，在确定了主余震参数的边缘分布以及Copula函数之后，通过给定主震参数的取值，就可以得到该条件下的对应余震参数的取值。

3.2 最优Copula函数的选择

在选择主余震参数的最优Copula函数之前，需采用Kendall秩相关系数判断参数相关性的大小。Kendall秩相关系数τ可由式(20)计算[26]

(20)

式中：x1，i和x2,i分别为主震和余震地震动参数的第i个观测值；N为样本容量;sign[·]为符号函数，当(x1,i-x1,j)(x2,i-x2,j)>0时，sign=1，否则sign=0。

主余震参数的Kendall相关系数,如表4所示。需要说明的是，由于Ⅰ0和Ⅳ类场地的实测记录数量较少，故没有分析其相关性。从表4中可以看出主余震的PGA之间保持着中等相关性，场地参数除了场地阻尼比之外保持着中等相关性。尽管主余震场地阻尼比ξg之间趋近于独立，但是笔者同样发现不同场地余震的场地土卓越圆频率ωg,aft和阻尼比ξg,aft之间均保持着中等负相关性(见表4)，因此可以采用Copula函数分析ωg,aft与ξg,aft的相关性。

表4 主余震参数之间的Kendall秩相关系数

根据主余震的参数之间的相关特性，本文采用6种Copula函数对主余震对应的峰值加速度、场地土卓越圆频率和调制函数参数以及余震的场地土卓越圆频率与阻尼比之间的相关结构进行拟合，对参数间的正负相关性和各种尾部相关性要求至少有一种Copula函数能描述。这6种Copula函数及其特征分别为：Gumbel Copula(具有上尾相关性，适合描述两个变量同时上涨的情况)、Clayton Copula(具有下尾相关性，适合描述两个变量同时下降的情况)、Frank Copula(可以同时拟合上、下尾相关且可以同时描述变量正相关性与负相关性)、Plackett Copula(对变量间相关性的正负无要求)、AMH Copula(对正负相关性无要求，但是不适合高相关性情况分析)和FGM Copula(为Plackett Copula关于(η-1)的泰勒展开式的前两项)。Copula函数的具体分布函数及其参数η,如表5所示。

表5 备选Copula函数模型[27]

对以上6种备选Copula函数同样进行AIC信息准则检验，即可选择出最优模型，检验的具体结果和最优Copula参数η，如表6所示。可以看出，PGA、场地参数ωg和时-频调制函数参数a的最优Copula模型以Plackett Copula为主；ωg,aft与ξg,aft的最优Copula模型同样以Plackett Copula为主。

表6 最优Copula模型

3.3 余震参数的条件概率密度函数与条件均值

在确定了主余震参数的边缘分布以及主余震参数之间的最优Copula函数之后，由式(16)～式(19)可得在主震参数条件下余震的条件概率密度函数和条件均值。不同主震峰值加速度条件的余震峰值加速度的概率密度函数和边缘概率密度的对比，如图4所示。由图4可知，在不同主震参数影响下，对应余震参数的概率密度函数区别显著，因此可以证明，考察余震参数时有必要考虑主余震参数之间的相关性。

图4 不同主震峰值加速度下的余震峰值加速度的概率密度函数对比

条件均值与观测值的对比图，如图5所示。由图5可知，Copula条件均值能够反映出给定主震参数条件下，余震参数的总体趋势。因此，可以利用Copula条件均值预测给定主震参数条件下余震参数的取值。

图5 Copula条件均值与观测散点图对比

在本文中，对主余震参数的条件均值曲线进行了最高8次的多项式拟合，得到了主余震参数的衰减关系式。表7中给出了Copula条件均值多项式拟合系数，其中，PGAmain和PGAaft的单位为g；ωg,main和ωg,aft的单位为rad/s；amain和aaft的单位为s-1。由于Ⅰ0类场地与Ⅳ类场地数据较少，因此不对这两类场地进行Copula均值计算，但是本文对总体记录的场地参数进行了分析并进行了多项式拟合来弥补这个问题。由此便建立了主余震参数之间的衰减关系，通过给定一套主震参数，便可以得到一套对应余震参数，这为工程应用提供了方便。

表7 Copula条件均值的多项式拟合系数

4 主余震型地震动过程的降维表达

4.1 非平稳地震动过程的降维表达

对于一个演变功率谱密度函数为SUg(t,ω)的零均值实非平稳地震动过程Ug(t)，其源谱表示为

(21a)

(21b)

式中:Δω为频率步长，Δω=ωu/N，ωu为截断频率，N为截断项数;{Xk,Yk}为一组标准正交随机变量，满足如下基本条件

E[Xk]=E[Yk]=0，E[XjYk]=0

(22a)

E[XjXk]=E[YjYk]=δjk

(22b)

式中：E[·]为数学期望；δjk为Kronecker-delta记号。

在式(21)中，由于随机变量Xk和Yk的概率分布未给定，因此不能直接用于模拟。定义正交随机变量集{Xk,Yk}(k=1,2,…,N)为如下形式

(23)

式中，φk(k=1,2,…,N)为一组在(0,2π)上均匀分布且相互独立的随机相位角。显然，式(23)定义的随机变量集{Xk,Yk}(k=1,2,…,N)满足基本条件式(25)。

将式(23)代入式(21a)中，即可得到非平稳地震动随机过程的传统随机相位模拟公式

(24)

式中,Ug1(t)即为采用传统随机相位角的谱表示模拟过程。可以看出传统模拟方法在本质上属于经典的蒙特卡洛方法，面临着高维随机变量所带来的巨大挑战。为了克服传统蒙特卡洛方法随机变量数量过大，模拟效率低下的缺陷，引入随机函数的降维思想[28]，将标准正交随机变量集{Xk,Yk}(k=1,2,…,N)定义为基本随机向量的正交函数形式，具体如下

(25)

4.2 主余震序列的构造

在主余震型地震动过程的降维模拟中，主震地震动过程和余震地震动过程均采用1.1节中的演变功率谱密度模型，其主要区别在于模型参数的取值。通过给定的场地条件、地震烈度，确定主震的峰值加速度和持时。对于主震的场地土卓越圆频率、阻尼比和调制函数，则根据场地类别采用参数识别结果的均值。进一步，利用表7的得到对应的余震参数，再把主震与余震的两套参数代入式(2)、式(4)与式(1)中便可得到主震和余震的演变功率谱密度模型。

这样，就实现了仅需两个基本随机变量即可精细的模拟主余震型地震动过程的目的。本文方法能够有效避免传统蒙特卡罗方法带来的样本数量庞大与样本集合概率信息不完备的问题，仅仅需要数百条样本即可在全概率层面上反映主余震型地震动过程的概率特性，具有与概率密度演化方法[30]结合的天然优势。

5 算例分析与验证

5.1 算例及分析

在本算例中，式(21)的计算参数为：频率截断项数N=1 600；截断频率ωu=240 rad/s；频率步长：Δω=0.15 rad/s；时间步长：Δt=0.01 s；主震和余震的模拟持时分别取为20 s和15 s。主震和余震其他的地震动参数如表8所示。需要说明的是，表8中主震的峰值加速度考虑8度设防地震，主震场地卓越圆频率、阻尼比和时频调制函数参数取为II类场地主震参数识别结果的均值。对于表8中余震参数，是利用所得主震参数通过表7求得的。

表8 主余震地震动参数取值

图6为用本文提出的方法模拟的Ⅱ类场地的主余震代表性时程曲线及模拟的144条主余震地震动过程代表性样本的均值及标准差与相应目标值的比较结果。从图6可以看出，余震衰减比主震更快，包含的能量更小，且144条代表性样本集合的模拟结果均与目标值拟合较好，这充分说明了本文方法的有效性。

图6 主余震代表性样本以及样本集合均值和标准差

5.2 主余震频谱特征验证

在本节中，将本文模拟方法得到的144条Ⅱ类场地的主余震代表性样本与筛选得到的主余震实测地震动记录对比。为方便起见，将模拟得到的余震时程与主余震实测记录均调幅至200 cm/s2。计算Ⅱ类场地的实测地震动记录的加速度反应谱与傅里叶幅值谱，并同本文的模拟结果进行对比，如图7所示。可以看出，不论是主震还是余震，实测强震记录均值都在模拟均值加减一倍标准差的范围内，这表明本文的模拟方法可以准确地反映主余震特征，具有良好的工程适用性。

图7 模拟的主余震地震动加速度的反应谱和傅里叶幅值谱与实测记录的比较

6 结 论

本文在非平稳地震动的演变功率谱密度模型的基础上，建议了该模型参数的识别方法，并利用实测主余震地震记录识别了模型参数。基于Copula理论，实现了主余震参数之间的相关性分析。结合谱表示-随机函数方法，建立了主余震型地震动的降维模型，生成了主余震型地震动的代表性时程。文中实现了从主余震实测记录出发、获取参数的边缘分布、到生成具有考虑参数相关性的主余震型地震动过程的代表性时程，再到与实测主余震型地震动记录的频谱特性进行对比的全过程，得出以下结论：

(1)主震的峰值加速度比余震有偏大的趋势；余震与主震相比，场地土卓越圆频率较大，阻尼比较小，时频调制函数参数a较大，这代表着余震能量比主震更小，衰减速度比主震更快。

(2)主余震参数之间大多保持着一定的相关性，其中峰值加速度PGA、场地土卓越圆频率和调制函数参数a之间保持着中等的相关性，而阻尼比之间表现为低相关性。不同场地的场地土卓越圆频率和阻尼比之间均保持着中等负相关性。此外，在不同主震参数取值的条件下，余震对应参数的概率密度函数有显著的区别。

(3)主余震型地震动过程的降维模拟方法仅需数百条样本即可在全概率信息上反应主余震地震动过程的概率特性，这为应用概率密度演化理论进行主余震型地震动作用下工程结构的随机动力反应分析与可靠度评估奠定基础。