基于半参数空间模型的房地产估值数据研究

张琳琳， 黄振生

(南京理工大学 理学院，南京 210094)

0 引 言

近几年随着市场经济的不断发展壮大，房地产估值数据越来越受到重视，探寻房价的影响因素及房价与这些影响因素间的相关关系已经成为统计学者的研究热点。很多研究人员对房地产估值数据进行了建模分析，Yeh[1]提出了一种创新的房地产估价方法——定量比较法，并通过房地产估值数据证明了定量比较方法比两种经典的享乐价格方法(多元回归分析和神经网络)更准确。同时，利用排序分位数方法，将房价的影响因素按照重要性从高到低的顺序排序为房屋到最近的捷运站的距离、步行圈内便利店的数量、房屋年龄和交易日期；Huang和Lou[2]考虑所观测到的房屋位置变量(纬度和经度)带有测量误差，从而利用带测量误差的单指标模型研究了房屋位置和房屋价格之间的关系；Wang[3]对影响房屋价格的因素进行了系统的分析，并针对近些年来的大众评价模型及方法进行了系统的文献综述；Wilhelmsson[4]在传统的房地产模型中考虑房地产数据的空间维度，采用传统的线性空间自回归模型解决问题，结果表明房价数据间存在空间自相关，而空间维度的加入解释了更多的价格变化。

在空间自回归模型中，部分线性空间自回归模型不仅保持了非参数空间自回归模型的灵活性，而且保持了参数空间自回归模型的解释力，从而在近些年引起了人们的广泛关注。Su和Jin[5]首次提出了部分线性空间自回归模型，并利用一种剖面拟极大似然方法来估计未知函数m(·)和参数向量(βT,ρ,σ2)T，然后系统地研究了所得估计量的渐近性质。为了考虑误差项的异方差性，Zhang[6]，Zhang和Yang[7]分别针对部分线性空间自回归模型提出了二元差分估计方法和工具变量估计方法；Li和Mei[8-9]提出了广义似然比检验法来检验非参数部分m(·)是否呈现一些有趣的参数形式，以及参数向量(βT,ρ)T是否满足某些线性约束条件；Wei和Guo[10]提出了一种半参数部分线性变系数空间自回归模型，它是标准空间自回归模型和部分线性空间自回归模型的推广。另外，为了估计未知的空间滞后参数、常数系数和系数函数，提出了一种基于局部线性方法的轮廓拟极大似然方法，为了检验空间效应的存在性，提出了一种广义似然比检验统计量，并利用基于残差的自举过程导出了检验的p值。

目前大多数对房地产数据研究的文献仍停留在传统的参数模型上，但众所周知，空间因素是影响房价的不可或缺的因素。虽然有一些文献[4]在模型中考虑空间自相关性，并基于此对相关变量给出更合理的参数解释，但却没有将自变量的非线性影响考虑在内，而往往解释变量与因变量的关系不是线性的，这就产生了一些局限性。基于上述考虑，针对现有的房地产估值模型中不包含空间自相关性以及非线性影响因素的问题，提出了可以灵活解释变量意义的部分线性空间自回归模型来拟合房地产估值数据，并对拟合结果给出合理解释。

1 数据介绍

房地产估值的市场历史数据集来自台湾新北市新店区。数据集包含2012-06—2013-05的414个样本，共6个变量，变量意义见表1，相关数据可见文献[1]。首先通过绘制变量间的散点图来判断房价(Y)与各影响因素(X1，X2，Z)间的相关关系，其中经度和纬度作为影响房价的位置信息，以空间权重矩阵的形式包含在模型中。从图1，图2，图3及现实意义中可以看出房价(Y)与房屋到最近的捷运站的距离(X1)和步行生活圈中便利店的数量(X2)存在线性关系，而与房屋年龄(Z)存在非线性关系。为了更进一步挖掘出变量数据中的隐含信息，进一步利用部分线性空间自回归模型对数据集进行拟合。

表1 房地产估值数据变量

图1 Y与X1的散点图

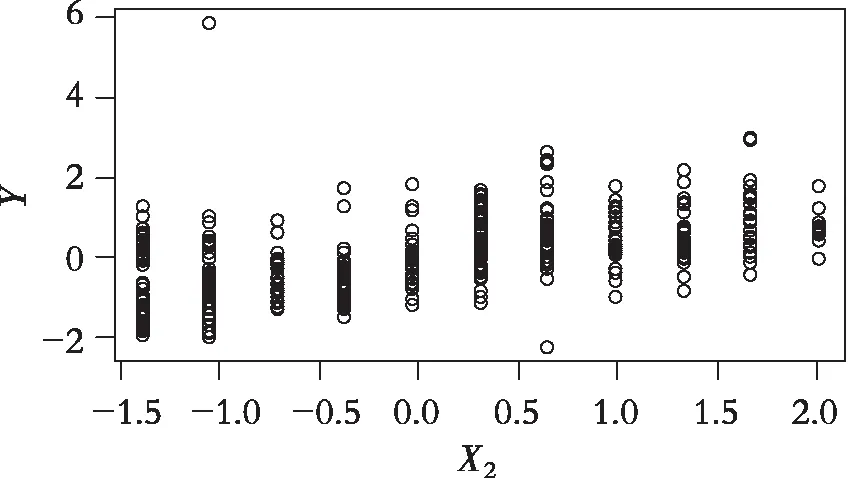
图2 Y与X2的散点图

图3 Y与Z的散点图

表2 变量间的相关系数矩阵

2 模型分析

部分线性空间自回归模型具有形式：

Yn=Xnβ0+m0(Zn)+ρ0WnYn+Un

(1)

(2)

在第二步中，考虑最大化下列似然函数

(Tn(ρ)Yn-Xnβ-mθ(Zn))

其中mθ(Zn)=(mθ(zn,1),…,mθ(zn,n))T，令Sn=(s(zn,1),…,s(zn,n))，在拟对数似然函数中，对于给定的ρ，β的QMLE估计为

σ2的QMLE估计为

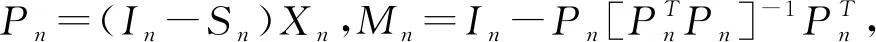
3 模型拟合

采用台湾新北市新店区2012-06—2013-05的房地产估值数据，共有414个样本，6个变量。利用变量中的经度(DLON)和纬度(DLAT)来建立空间权重矩阵，将数据应用于部分线性空间自回归模型Y=X1β1+X2β2+m(Z)+ρWnY+U中，并对指标变量进行标准化处理。令Wn=(wij)，wij=max(1-dij/d0,0)，其中dij为欧几里得距离，选择阈值距离d0为0.05，并对空间权重矩阵Wn进行标准化，使其行和为1。此外利用EPANECHNIKOV核函数，通过大拇指法则选取带宽h=0.317 6进行估计。部分线性空间自回归模型指标参数的估计值见表3。

表3 未知参数估计值

未知函数的拟合结果如图4所示。

图4 m(Z)的估计

从表3可以看出，单位面积房价(Y)指标之间存在负空间相关性，房屋到最近的捷运站的距离(X1)与房价(Y)呈负相关关系，即离最近的捷运站距离越近，房价越高；而步行生活圈中便利店的数量(X2)与房价(Y)呈正相关关系，便利店数量越多，房价越高；这与实际意义相符，同时也证明模型具有现实意义。从图4可以看出房价(Y)与房屋年龄(Z)之间存在非线性关系，部分线性空间自回归模型可以较好地拟合房地产估价数据。

4 结 论

采用部分线性空间自回归模型对房地产估值数据进行统计研究，与之前文献研究所不同的是，加入了空间和非线性因素的影响，对于部分线性空间自回归模型的估计问题，首先利用局部多项式估计法对非参数部分进行估计，从而得到含参数形式的非参函数估计，再将此估计表达式代入对数似然函数中，通过极小化对数似然函数得到参数部分的估计。在房地产估值数据的拟合过程中，不同于之前文献中计算空间相关矩阵的方法，利用经度、纬度计算房屋之间的欧几里得距离，从而将空间位置因素以空间相关矩阵的形式引入模型中。结果表明，房价数据之间存在着空间相关性，房屋到最近的捷运站的距离与房价呈负相关关系，而步行生活圈中便利店的数量与房价呈正相关关系，这与现实意义上的解释是相通的。另外房屋年龄与房价之间的非线性关系也被体现出来。部分线性空间自回归模型能更加客观和灵活地解释房地产估值数据的现实意义。